Разработка алгоритма передачи данных по каналу связи в программной среде MATLAB

DOI:

В системе связи с одной несущей длительность символа должен быть намного больше, чем время задержки, чтобы избежать межсимвольной интерференции. Однако достичь этого можно только за счет снижения скорости передачи данных, так как скорость передачи обратно пропорциональна периоду символа. В системе связи с нескольки-

ми несущими (например, FDM) общая доступная полоса пропускания разделяется на поддиапазоны для параллельной передачи нескольких несущих (поднесущих). Однако при высокой скорости передачи может возникнуть интерференция между поднесущими, так как высокая скорость достигается за счет их близкого расположения в спектре. Для того чтобы избежать интерференции и между символами, и между поднесущими, в системах связи распространено использование мультиплексирования с ортогональным частотным разделением – OFDM [1].

Во-первых, ортогональность позволяет поднесущим быть близко расположенными, и даже накладываться друг на друга, без помех между ними, так как передача информации на каждой из них не влияет на передачу информации на соседних (рис. 1) [2]. Это следует из математического определения ортогональности, означающего нулевое скалярное произведение сигналов разных поднесущих. Таким образом, в случае смещения одной из поднесущих по частоте при передаче, она займет место другой поднесущей, сигнал которой при демодуляции будет равен нулю, что показывает отсутствие интерференции между поднесущими. Физически ортогональность обеспечивается в случае, когда за время длительности одного символа несущий сигнал будет совершать целое число колебаний.

Помимо этого, такое размещение позволяет более эффективно использовать доступную полосу частот.

Во-вторых, низкая скорость передачи данных каждой поднесущей подразумевает боль- шую длительность символов, что значительно уменьшает межсимвольные помехи [3; 4].

Для борьбы с межсимвольной интерференцией в OFDM используется защитный или охранный интервал (Guard Interval, GI), как показано на рис. 2. Обычно в качестве защитного интервала используют так называемый циклический префикс. Префикс представляет собой циклическое повторение окончания OFDM-символа. Он добавляется перед передаваемым OFDM-символом в передатчике и удаляется при приеме символа в приемнике. Наличие защитного интервала создает временные паузы между отдельными символами, и если его длительность превышает максимальное время задержки сигнала в результате многолучевого распространения, то межсимвольной интерференции не возникает.

Разработка программного алгоритма велась с помощью среды программирования Matlab, так как в Matlab предусмотрено большое количество различных математических операций, что позволяет не писать развернутый код этих операций, тем самым позволяя выделить основные физические процессы в алгоритме, что упрощает его разработку.

д

1011001011 .

п потоков

1101100010 J

д n поднесущих

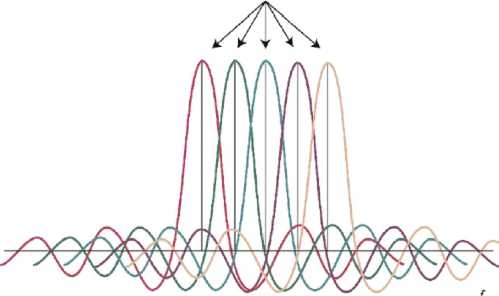
Рис. 1. Мультиплексирование с ортогональным частотным разделением

Без циклического префикса

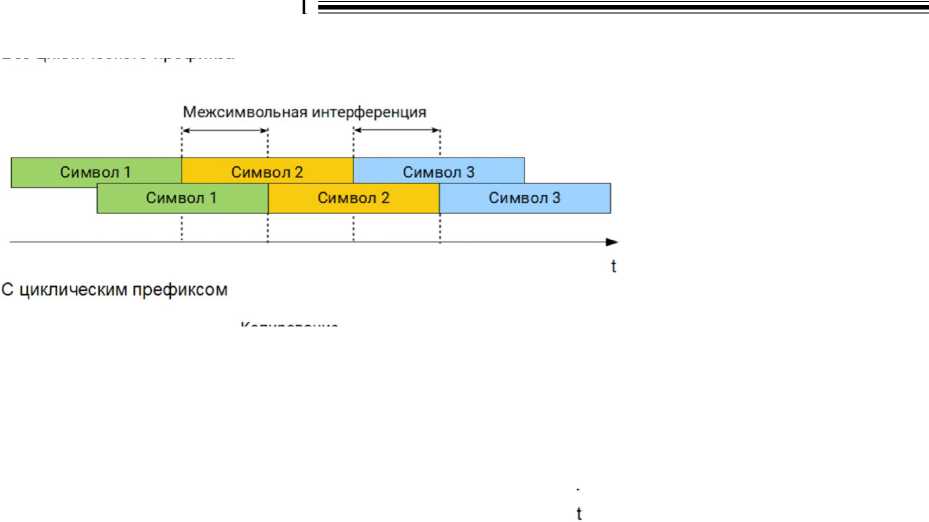
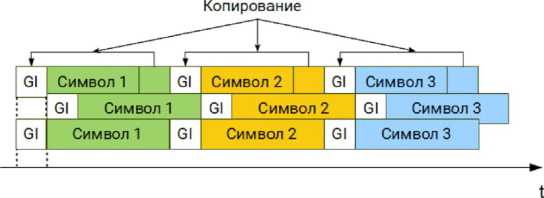
Рис. 2. Защитный интервал и межсимвольная интерференция

Первым этапом в работе алгоритма является ввод параметров для последующего моделирования, таких как, например, размер циклического префикса, значение отношения сигнал/ шум и др. Затем происходит обработка изображения, при которой данные из трехмерного массива преобразуются в двоичный код (поток данных), после чего полученный поток битов (0 и 1) разделяется на битовые символы.

Далее необходимо модулировать сигнал в соответствии с выбранным методом модуляции (при разработке алгоритма использовалась квадратурная фазовая манипуляция), и после этого с помощью обратного быстрого преобразования Фурье произвести перенос данных из частотной области во временную.

Затем к данным добавляется циклический префикс и происходит преобразование parallel-to-serial, то есть из параллельных данных в последовательные. Далее к полученному сигналу добавляется белый гауссовский шум, сигнал передается по каналу связи и попадает на приемную сторону, где с данными происходят обратные операции преобразования.

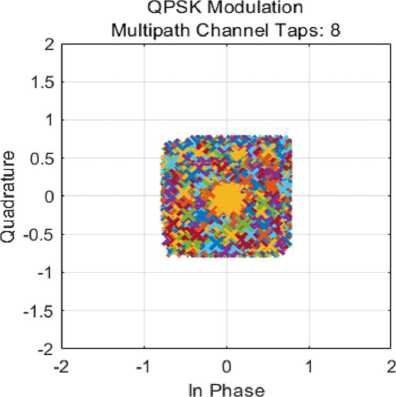
На завершающем этапе работы алгоритма из полученного после демодуляции двоичного потока данных формируется матрица изображения и происходит вывод результатов: на экран выводятся изначальное (оригинальное) и восстановленное после передачи изображения, строится график сигнального созвездия, вычисляется показатель BER – это количество ошибочных битов, деленное на общее количество переданных битов за исследуемый интервал времени.

После запуска и успешной работы разработанного программного алгоритма были получены следующие результаты, представленные на рис. 3.

Стоит отметить, что по рисунку 3 видно, что восстановленное из переданного сигнала изображение, почти не отличается от оригинала, так как показатель BER составляет всего 0,11, что говорит о высокой точности передачи данных.

В завершении была проведена оценка работы алгоритма. Для этого изменялось значение отношения сигнал/шум (SNR) и записывалось результирующее значение BER. На основе серии проведенных экспериментов был построен график зависимости значения показателя BER от значения SNR, представленный на рис. 4.

Таким образом, можно видеть, что при увеличении параметра SNR, задававшегося на начальном этапе работы алгоритма, в результате уменьшается показатель BER, то есть количество ошибок становится меньше.

Соответственно, можно сделать вывод об адекватной работе разработанного алгоритма, а также на основе полученных данных можно судить о довольно высокой точности передачи графической информации с помощью разработанного алгоритма.

Transmit Constellation

Trancmit Image

Рис. 3. Результаты работы алгоритма

Recovered image BER: 0.11

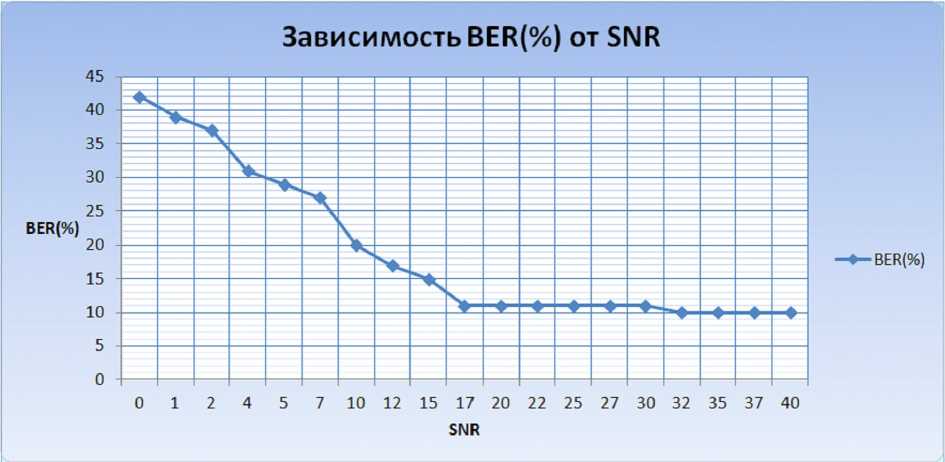
Рис. 4. График зависимости BER от SNR