Разработка алгоритма расчета геометрических параметров подводной и надводной частей судна

Известно, что значения параметров, определяющих динамические характеристики судна, зависят прежде всего от состояния его загрузки, производными которой являются осадка носом и кормой. Следовательно, для получения значений указанных параметров после загрузки судна по заданному грузовому плану необходимо рассчитать значения осадок носом d f и кормой d a и, таким образом, условно разделить судно на надводную и подводную части.

Гидродинамические характеристики судна определяются геометрическими параметрами его подводной части, а аэродинамические – надводной. Для получения математической модели судна с целью моделирования его движения необходимо определить и рассчитать ряд параметров, которые зависят от геометрии его надводной и подводной частей судна: номер теоретического кормового шпангоута, пограничного между шпангоутами U - и V -образной формы; объемное водоизмещение V ; площадь действующей ватерлинии S ; площадь погруженной части мидель-шпангоута ω м ; координаты центра тяжести (ЦТ) погруженного объема x c , z c ; абсциссу ЦТ площади ватерлинии x f ; площадь смоченной поверхности Ω ; площадь погруженной части диаметрального батокса F dp ; площадь, дополняющую контур кормовой части диаметральной плоскости (ДП) судна до прямоугольника F_a и др.

Кроме того, для моделирования движения судна в реальных условиях плавания с учетом воздействия ветра и волнения, ограниченной глубины (мелководья) требуется рассчитать ряд дополнительных параметров, а именно моменты инерции массы судна I_y и I_z относительно поперечной y и вертикальной z осей координат, соответственно; коэффициенты, определяющие характер взаимодействия корпуса танкера и окружающих его волн при движении в условиях волнения µ _{1 кр} , µ _{2 кр} ; площади проекций надводной части танкера на диаметральную плоскость S dp и плоскость мидель-шпангоута S m ; абсциссу x a и аппликату z а центра парусности.

С этой целью нами был разработан алгоритм и соответствующая ему компьютерная программа, позволяющие достаточно просто, но с приемлемой точностью (погрешность вычисления не более 5 %) производить последовательный расчет значений гидродинамических и аэродинамических характеристик судна и вводить их в математическую модель с учетом заданных условий плавания.

Под заданными условиями плавания подразумеваются:

• –    состояние загрузки танкера, характеризующееся водоизмещением P и координатами его ЦТ x_g , z_g ;

• –    состояние внешней среды района плавания, а именно: скорость ветра υ а , его направление q а , высота волны h 3 % , направление фронта волны q w , скорость течения υ т и его направление Ψ st , глубина H .

• 2.    Формирование базы данных расчетов

Для выполнения расчетов всех перечисленных выше параметров используются заданные в табличной форме координаты точек поверхности корпуса судна (в нашем случае т/к "Астрахань"). Объем заложенных в память компьютера данных определяется, исходя из следующих соображений: максимум точности, значение которой уже упоминалось, минимум объема памяти компьютера.

Как известно, корпус судна может быть задан рядом шпангоутных сечений, причем их количество вовсе не обязательно должно быть стандартным (21 шпангоут). Выбор количества

Юдин Ю.И. Разработка алгоритма расчета геометрических параметров… шпангоутных сечений корпуса определяется характером его кривизны в различных районах судна. Так, например, в районе цилиндрической вставки можно не отступать от стандартного количества шпангоутов, а в концевых участках их количество желательно увеличить с учетом заданной точности расчетов (в рассматриваемом примере общее количество шпангоутов равно 50). Координаты точек штевней и контура надводной части ДП судна задаются отдельно.

Количество и порядок расположения точек на каждом шпангоутном сечении определяются из условия наилучшей аппроксимации участков кривых ломаной линией. Нумерация точек в контуре соответствует движению против хода часовой стрелки; первая точка (а их не более сорока) расположена в ДП, там, где она пересекается с основной плоскостью (ОП). Учитывая симметрию корпуса относительно ДП, достаточно в базу данных включить только половину точек контура сечения.

Надводная часть корпуса, надстройки, рубки и прочие надпалубные постройки, имеющие сплошную поверхность, задаются координатами точек, расположенных по периметру контура ДП. На рис. 1 показана проекция танкера на ДП, построенная с использованием базы данных, полученных по чертежам т/к "Астрахань". Здесь же нанесена действующая ватерлиния для определенного варианта загрузки, показаны надводная и подводная части танкера.

Необходимо отметить, что такой способ представления корпуса и других частей судна (назовем его точечный) в компьютере позволяет определить любой интересующий нас параметр подводной и надводной частей судна практически при любом варианте загрузки и, как следствие, посадки.

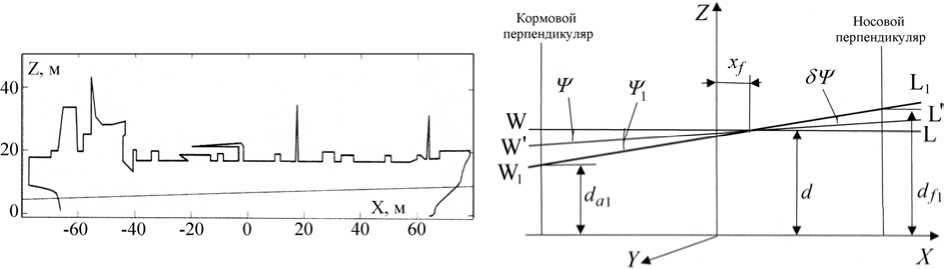
Рис. 2. Определение осадок носом d f 1 и кормой d a 1 с учетом состояния загрузки танкера

Рис. 1. Проекция танкера на ДП, построенная с использованием базы данных

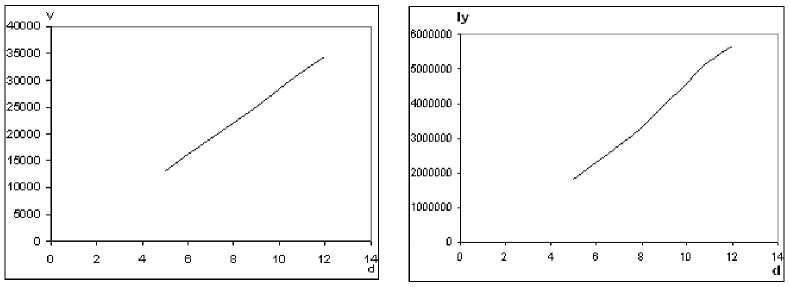
Рис. 3. Зависимость объемного водоизмещения V и продольного момента инерции водоизмещения I y т/к "Астрахань" от осадки d

Эти же зависимости в аналитической форме выглядят следующим образом:

V = 2,435 - 10³ + 1,35 - 10³ - d +194,969 - d ² - 7,045 - d ³;                    (1)

I y = 2,308 - 10⁶ - 6,623 - 10⁵ - d + 1,402 - 10⁵ - d ² - 5,124 - 10³ - d ³.             (2)

Поскольку в дальнейшем нам потребуется решить обратную задачу, т.е. определить значение осадки d по известному значению водоизмещения V , выражение (1) приведем к соответствующему этой задаче виду:

d = 5 806 - 10 ⁸ + 4.221 - 10 ' - V - 3,738 - 10^-9 - V ² + 4,551 - V ³. (3)

• 3)    Для выполнения следующего шага вычисления необходимо нанести действующую ватерлинию на теоретический чертеж. Эту задачу можно решить, используя уравнение моментов относительно ЦТ площади действующей ватерлинии F ( Власов , 1959) (рис. 3):

0,5tg³ у^ + tg у [ V ( z c - z g ) + I yf ] + V ( X c - X g ) = 0.

Учитывая малое значение угла дифферента судна ( у < 5 ° ) в эксплуатационных условиях, членом уравнения (4), содержащим tg³ у , можно пренебречь. В этом случае уравнение для определения угла дифферента запишется в виде:

у = arctg{- V ( X c - X g ) / [ I yf + V ( z c - z g )]}. (5)

Все необходимые параметры, входящие в расчетную формулу (5), определяются для посадки судна на ровный киль с осадкой d , найденной по уравнению (3), при этом V = P / р ( р = 1,025 т/м³). Развернув условную ватерлинию на угол у , сделаем следующий шаг на пути к определению положения действующей ватерлинии. Для этого рассчитаем поправку к углу дифферента первого приближения Ау 1 , учитывающую разность значений параметров заданной ватерлинии ( WL ) и ватерлинии, наклонной по отношению к ней на угол у ( WL ‘ ). Она определяется из известного уравнения моментов главных сил, действующих на танкер относительно F' - ЦТ площади ватерлинии WL' (известно, что при равнообъемном наклонении, а в данном случае - с учетом малости у - это так, координаты ЦТ площади ватерлинии остаются практически неизменными):

Юдин Ю.И. Разработка алгоритма расчета геометрических параметров…

• x' - отстояние ЦТ площади проекции ватерлинии W L' на координатную плоскость xoy от оси oy :

+ L /2

x = (2 / S ) j xydx .                                            ⁽¹⁰⁾

• - L /2

Для вычисления определенных интегралов в выражениях (8-10) используется один из приближенных способов интегрирования, а именно правило Чебышева. Операция вычисления при ручном счете более продолжительная по сравнению с другими способами (правило трапеций, правило Симпсона и др.), но выигрывает в точности, что важнее с учетом того, что расчет ведется с использованием ЭВМ.

Итак, решая уравнение (6) относительно 8у 1 , получаем:

8y ₁/cos² у = { p V ( X f - x c ) - A ( X f - x g ) - [ A ( d - z g ) -- p V ( d - Z c )]tg y }/[ A ( d - Z g ) - p V ( d - Z c ) + p I yf (1 + tg² у )].

Тогда положение действующей ватерлинии в первом приближении определится углом у 1 , вычисленным по формуле:

у 1 = (tg y + 8y ₁/ cos ² y ).

Проведя ватерлинию W ₁ L ₁ относительно исходной ватерлинии и применяя рассмотренную процедуру расчета, во втором приближении находим

8y ₂/cos² у ₁ = { p V ₁( x f - x c 1 ) - A ₁( x f - x g ) - [ A ₁( d - z g ) -- p V i ( d - Z c i )]tg у } / [ A i ( d - Z g | - p V i ( d - Z c i ) + p I yf (1 + tg² y)].

у ₂ = arctg(tg y ₁ + 8y ₂/cos² y ₁).

Процесс приближения к заданной ватерлинии может быть остановлен с учетом практически возможной точности определения угла дифферента, а она, как известно, не превышает 0,1 ° . Следовательно, если

I уп +i - yn | < 0,1°, вычисления можно завершить, приняв последнее значение у за действующее. Процесс последовательного приближения можно остановить и по другим соображениям.

Учитывая значение осадки судна d и найденное описанным здесь способом значение угла дифферента у, можно перейти к расчету параметров, характеризующих посадку судна, т.е. осадки носом df = d + (0,5Lpp -xf)tgy                                     (15)

и кормой da = d- (0,5Lpp + xf)tgy,                                       (16)

где L_pp - длина между перпендикулярами; у - угол дифферента, найденный на последнем шаге приближения.

Определив значения осадок оконечностей судна при соответствующей его загрузке, мы можем переходить к расчету параметров математической модели; при этом необходимо учитывать, что разработанный алгоритм расчета позволяет определять как гидродинамические, так и аэродинамические характеристики судна.

4. Заключение

Предложенный выше алгоритм расчета геометрических параметров судна (подводная и надводная часть) может быть достаточно просто реализован при наличии соответствующих судовых документов. Точность расчетов с использованием предлагаемого алгоритма может регулироваться изменением количества шпангоутных сечений и точек на их контуре, тем самым устраняется зависимость точности расчета от конфигурации корпуса и других конструктивных особенностей судна. Несмотря на то, что алгоритм расчета разрабатывался для выполнения модельных экспериментов в области управляемости судна, он может быть использован с целью проведения научных исследований и при решении практических задач по расчету мореходных качеств судна. Алгоритм расчета легко программируется и может быть представлен в виде отдельного блока в любой прикладной программе, где требуется определение мореходных качеств судна.