Разработка алгоритма решения задач методом конечных элементов для создания математических моделей «кость - фиксатор»

Стремительно растущие требования социума к качеству лечения переломов привели к разработке в течение нескольких последних десятилетий современных оперативных методик, обеспечивающих высокую стабильность фиксации за счет биосовместимости использующихся конструкций, совершенствования технико-технологических характеристик процессов их изготовления, облегчения процесса установки и удаления имплантов после консолидации перелома. Успехи в совершенствовании методик лечения переломов достигнуты в результате накопления клинического опыта и анализа всех стадий лечения с применением методов биомеханики [3].

В ходе поиска дальнейших возможностей улучшения исходов лечения диафизарных переломов костей голени (ДПКГ) было произведено биомеханическое исследование качественных характеристик их остеосинтеза различными способами в зависимости от степени и варианта фрагментации ББК, классификационного типа перелома. Учет анизотропных свойств материала кости, решение контактной задачи теории упругости позволяют представить картину распределения напряжений в элементах послеоперационной системы «кость – фиксирующая кон

струкция» с высокой степенью достоверности [1], [4]. При создании математической модели использовалась подготовка предварительных моделей с помощью рентгенограмм и скиаграмм переломов, а также серии топограмм ББК, импортируемых с мультиспирального компьютерного томографа фирмы SIEMENS. Компьютерное моделирование с применением метода конечных элементов на основе томограмм (рис. 1), выполненных с шагом 0,5 мм, обеспечило создание качественной модели ББК, подобной биологическому прототипу; кроме этого рассматривалось напряженно-деформированное состояние фиксатора при функциональной нагрузке.

Сложные геометрические модели биологических объектов создавались в системе трехмерного проектирования по результатам данных компьютерной томографии. Срезы в поперечном сечении кости обработаны в системе трехмерного проектирования SolidWorks. На их основе построены плоские сечения, которые объединялись в объемную модель кости. Затем формировалась твердотельная 3D-модель (рис. 2).

Трехмерные геометрические модели фиксирующих устройств строились на основе чертежей и схем с сохранением их конструкционных свойств и размеров (рис. 3).

Разработка алгоритма решения задач методом конечных элементов для создания математических моделей...    49

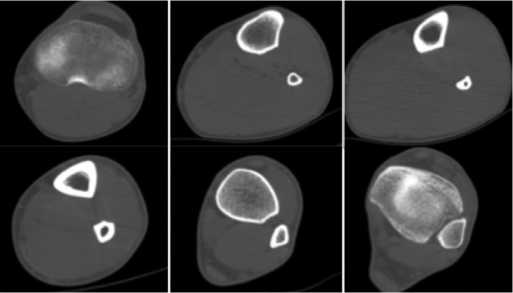
Рис. 1. Томограммы ББК (шаг 0,5 мм)

Рис. 2. 3D-модель большеберцовой кости

Рис. 3. Модель интрамедуллярного фиксатора

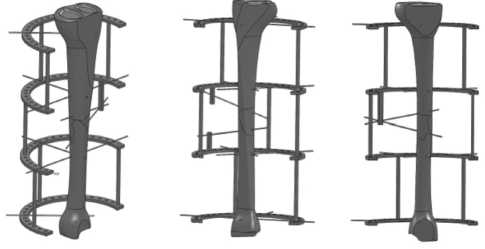
Рис. 4. Модель фиксации ДПКГ аппаратом Г. А. Илизарова (во фронтальном разрезе)

Далее геометрические модели кости и фиксаторов импортировались в систему конечноэлементного моделирования, где и проводились расчеты напряженно-деформированного состояния систем (рис. 4).

Задача о нагружении системы «большеберцовая кость – фиксатор» решалась в трехмерной постановке. В программном комплексе Ansys решались стационарные уравнения теории упругости в перемещениях Навье – Ламе [2]. Нижний торец кости жестко закреплялся, а к верхнему концу (суставная площадка проксимального эпифиза большеберцовой кости) прикладывалась осевая нагрузка, определенная для удобства расчетов в 450 Ньютон (Н). Между элементами фиксатора (аппарат Илизарова, интрамедуллярный гвоздь) и костными отломками ставились условия контакта с трением. Коэффициент трения составлял 0,55. Механические свойства фиксаторов задавались на основе технических данных изготовите-

И. П. Лозовик, Р. И. Мельцер, М. Ф. Баракат ля. Механические свойства кости задавались на основе литературных данных. Материал кости и фиксаторов предполагался изотропным идеально-упругим.

Таким образом, алгоритм решения задачи методом конечных элементов состоит из следующих шагов:

• 1.    Выбор математической модели. Это означает, что необходимо выбрать соответствующий конечный элемент или задать дифференци-

• альные уравнения, описывающие исследуемый процесс;

• 2.    Создание или импорт геометрической модели;

• 3.    Задание свойств материалов, граничных и начальных условий, параметров решателя;

• 4.    Разбиение модели на конечно-элементную сетку;

• 5.    Решение задачи;

• 6.    Визуализация и обработка полученных результатов.

AN ALGORITHM DESIGN FOR SOLVING PROBLEMS BY THE FINITE ELEMENT METHOD TO CREATE THE “BONE – FIXATOR” MATHEMATICAL MODEL