Разработка алгоритма сжатия изображений на основе статистических зависимостей между элементами изображения

Развитие цифрового телевидения, цифровой фотографии, систем передачи видеосигналов требуют передачи большого объема бит. Поэтому проблема экономии ресурсов для хранения и передачи информации в цифровом виде является весьма актуальной. Для получения компактного представления изображений в цифровой форме в настоящее время разработано огромное количество алгоритмов. Однако многие из них требуют больших вычислительных ресурсов на их реализацию.

В данной работе предлагается алгоритм сжатия цифровых полутоновых изображений (ЦПИ), требующий для своей реализации минимальных вычислительных ресурсов, при высоком качестве восстановления изображения.

k -РДИ можно передавать либо последовательно, либо одновременно по k двоичным каналам. Наличие корреляции между элементами РДИ свидетельствует о статистической избыточности

между ними, устранить которую можно за счет сокращения количества элементов изображения

передаваемого по каналам связи.

В данной работе предлагается разбить изображение с размерами r х s на квадраты размерами 3х3 элемента. На рис. 1 представлен фрагмент изображения из девяти элементов, в котором

пунктирные линии указывают на наличие статистических связей между элементами ЦПИ, О, □ -элементы изображения, передаваемые и непере-

даваемые по каналу связи, соответственно.

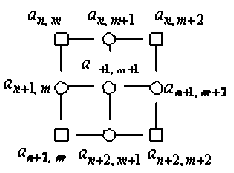
Рис.1. Модель фрагмента изображения

Постановка задачи

Необходимо разработать алгоритм сжатия ЦПИ, представленных k -разрядными двоичными числами, требующий для своей реализации минимальные вычислительные ресурсы.

Цифровое полутоновое изображение разбивается на k -разрядных двоичных изображений (РДИ). Если k -разрядные выборки из ЦПИ являются коррелированными, то в РДИ присутствует статистическая связь между соседними элементами по горизонтали и вертикали. Учитывая статистические свойства большинства ЦПИ, их

На фрагменте изображения (рис. 1) элементы a n , m , a n , m + 2 , a n + 2, m , a n + 2, m + 2 с учетом корреляционных связей между элементами РДИ можно восстановить по принятым окрестным элементам a n , m + 1 , a n + 1, m , a n + 1, m + 2 , a n + 2, m + 1 по формулам (1) и (2).

Например, вероятности значений элемент a _{n , m} можно вычислить по формулам:

P ^{( a} n , m = 0 ) = P ^{( a} n , m + 1 = 0 )- ^{( 1 n} ii ^{) +} P ^{( a} n , m + 1 = ^{1 ) x X (} 1 ⁿ ij ^{) +} P ⁽ an+1, m = ° ) ⁽ 2 ^П ii ^{) +} P ^{( a} n + 1, m = 0 (^ j ^{) ;}

можно аппроксимировать многоуровневыми дискретнозначными марковскими процессами [1], а РДИ – марковскими процессами с двумя равновероятными дискретными значениями ( P ₁ = P ₂) и одношаговыми матрицами вероятностей пере-

ходов (МВП) по горизонтали ¹ П =

π ₁₁

π ₂₁

π ₁₂

π ₂₂

P(an, m = 1) = P(an, m+1 = 1)- (1Пii )+ p(an, m+1 = o)x (2) X ( П j )+ P(an+1, m = 1) ( Пii )+ P(an+1, m = o) ( n j ), где 1Пи, 1nij, 2 пи , 2 nj - элементы МВП по горизонтали и вертикали РДИ. Предполагается, что элементы изображения an m+i и

a n + 1 m ( n = 1, r ; m = 1, s ) принимают равновероятные значения.

Элемент РДИ a _{n , m} принимает значение 0, если P ( an , m = 0 ) >  P ( a n , m = 1 ) , в противном случае a _{n , m} =1. Аналогично определяются значения э^{лементов} an , m + 2 , an + 2, m , a n + 2, m + 2 •

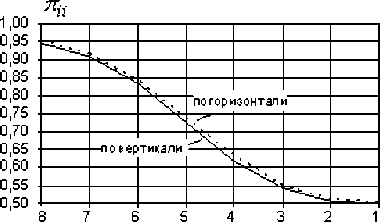
Для определения элементов было получено усредненное распределение вероятностей переходов ¹ _{π ii и} ² _{π ii} по горизонтали и вертикали в k РДИ на основе большого числа выборок реальных изображений (рис. 2).

H 0 M 6 p б нт о E O й пп О с к о ст и

Рис.2. Усредненное распределение вероятностей переходов (8 – старший разряд; 1 – младший разряд)

Анализ графиков показывает,что вероятности пе- рехода по горизонтали и вертикали имеют идентичный характер.Однако вероятности перехода по вертикали обычно меньше на 3 – 5 %,чем по горизонтали.

Ниже приведен пример определения значений элементов.

Пример. Если an , m + 1 =0, a^ , m =0 и вероятности переходов ¹ π _ii =0,84, ² π _ii =0,8, то P ^(an,m = ^{o )} = P ^(an, m + 1 = 0 )- ^{( 1 n} ii ^{) +} P ^(an + 1, m = ⁰ ) ⁽ 2 ⁿ ii ) = = 0,5 • 0,84 + 0,5 • 0,8 = 0,82 , а p ( a n , _m = 1 ) = 0,18 •

Так как P ( a _{n m} = o ) >  P ( a _{n m} = 1 ) , то a _{n m} = 0 •

Если a n , _{m +} i = 0 , a _{n + 1}, _m = 1 и вероятности

1                            2

переходов       π _ii = 0,84,       π _ii = 0,8, то

= ⁰ ) ⁽ 1 ⁿ ii ^{) +} P ^{( a} n + 1, m ~ 1 ) ( 2 ^П 42 ) =

Р\а an, m

^{о ) P} ( ^a n , m + 1

= 0,5 ■ 0,84 + 0,5 ■ 0,2 = 0,52 , а p ( a n, m = 1 ) = 0,48 •

В РДИ младших разрядов, в которых вероятности переходов ¹ π _ii ≈ 0,5, ² π _ii ≈ 0,5, элементы РДИ могут быть сформированы на основе генератора случайных чисел, равномерно распределенных в интервале [0,1].

Известно, что для создания одномерного массива из двухмерного необходимо выбирать обход массива элементов изображения так, чтобы «разрывов» было как можно меньше. Это позволяет уменьшить задержку кодирования. Сжатие будет лучше, если каждая область двумерного массива не рассредоточена по всему одномерному массиву, а сконцентрирована компактно. Поэтому для создания одномерного массива был предложен вариант обхода плоскости, представленный на рис.3.

	1			f			11
I	*	1	I	I	1D	11	1*	11
	1			I			11
	If			I!			11
»	II	II	II	Il	11	ID	11	1f
	ID			I*			11
	11			If			«
11	1*	11	11	11	«	*1	41	41
	11			11			44

Рис. 3. Обход плоскости для создания одномерного массива

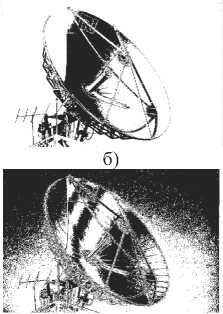
Другой особенностью ЦПИ является то, что между соседними РДИ, принадлежащими старшим разрядам ЦПИ, имеется большая корреляция. На рис. 4 показаны три РДИ восьмиразрядного изображения «Антенна».

а)

в)

г)

Рис. 4. Исходное изображение «Антенна» (а), РДИ седьмого (б), шестого (в) и пятого (г) разрядов изображения

Из сравнения РДИ шестого (в) и седьмого (б) разрядов следует, что большая часть элементов шестого разряда перешла в другое состояние. А из сравнения РДИ пятого (г) и шестого (в) разрядов следует, что большая часть элементов пятого разряда повторяет элементы шестого разряда.

Сжатие изображения, в данном случае, можно обеспечить за счет замены большого количества областей, в которых элементы изображения повторяются или переходят в противоположные элементы, счетчиками повтора или пропуска соответствующих областей. Графики на рис. 5а,б подтверждают большую зависимость повторяемых и пропускаемых областей элементов от номера РДИ.

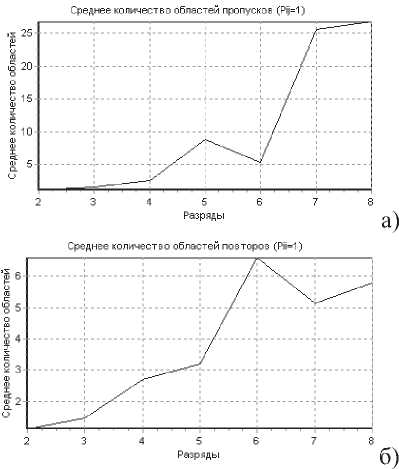
Рис. 5. Зависимости среднего количества пропускаемых (а) и повторяемых (б) областей от номера РДИ «Антенна»

Алгоритм сжатия изображения

• 1.    РДИ разбивают на квадраты 3х3 элемента (рис. 1).

• 2.    Элементы в РДИ старшего разряда кодируются следующим образом. Если подряд следующие области повторяются, то передаются элементы одной первой встретившейся облас^ти a n, m + 1 , a n + 1, m , a n + 1, m + 1 , a n + 1, m + 2 , a _{n +} 2, _{m +} 1 и количество их повторов.

• 3.    Одновременно производится сравнение элементов a n, m + 1 , a n + 1, m , a n + 1, m + 1 , a n + 1, m + 2 , a n + 2, m + 1 в ^{( l} - 1 ) ^-ом РДИ с соответствующими элементами l -го РДИ ( l = 1, к -номер разряда двоичного числа представления ЦПИ).

• 4.    Если элементы ( l – 1)-го РДИ совпадают с элементами l -го РДИ, то передается количество повторов элементов l -го РДИ.

• 5.    Если элементы ( l – 1)-го РДИ переходят в противоположные, то передается количество пропускаемых областей.

• 6.    Если не все элементы области ( l – 1)-го РДИ совпадают или переходят в противоположные, то в канал связи передаются значения элементов области ( l – 1)-го РДИ.

• 7.    Если значения передаваемых областей повторяются, то передаются элементы одной области a n, m + 1 , a n + 1, m , a n + 1, m + 1 , a n + 1, m + 2 , a n + 2, m + 1 ( l – 1)-го РДИ и количество их повторов.

Возможный формат передаваемых данных старшего РДИ представлен на рис. 6.

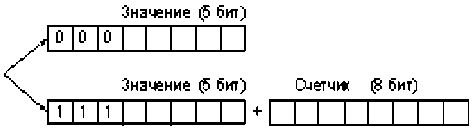
Рис. 6. Формат передаваемых данных старшего РДИ

Для однократной передачи в трех верхних битах файла передаются три нуля. А в случае многократной передачи в трех верхних битах передаются единицы, затем значения передаваемых бит и количество их повторов. Таким образом, счетчик может принимать значения от 2 до 255.

Возможный формат передаваемых данных младших РДИ представлен на рис. 7.

Счетчик повтора (6 бит)

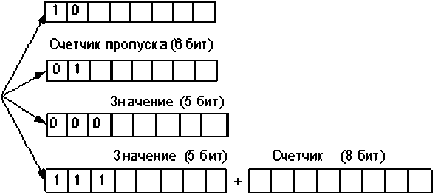
Рис. 7. Формат передаваемых данных младших РДИ

В случае сравнения РДИ для передачи количества повторяемых или пропускаемых областей два верхних бита файла отводятся для передачи информации о передаваемых элементах (рис. 6). А счетчик может принимать значения от 1 до 64.

Для восьмиразрядных изображений максимальный коэффициент сжатия составит 76,8, а для четырехразрядных – 82,3.

Таким образом, сжатие изображений происходит:

• 1)    за счет исключения элементов, которые можно восстановить по корреляционным связям;

• 2)    за счет того, что в исходном изображении встречаются цепочки из одинаковых элементов;

• 3)    за счет того, что в соседних РДИ имеются большие области, в которых элементы изображения либо повторяются, либо переходят в противоположные элементы.

Алгоритм восстановления изображения

• 1.    Определяют элементы a _n , _{m +} 1 , a _{n +} 1, _m , a n + 1, m + 1 , a n + 1, m + 2 , a n + 2, m + 1 ^(рис. 1) и количество их повторов в старшем РДИ из считанного файла.

• 2.    По известным значениям элементов ^a n, m + 1 , a n + 1, m , a n + 1, m + 1 , a n + 1, m + 2 , a n + 2, m + 1 , имея усредненные вероятности переходов

• 3.    Одновременно по элементам a n m + i , a n + i, m , a n + 1, m + 1 , a n + 1, m + 2 , a n + 2, m + 1 в ^старшем РДИ определяют элементы a _{n , m} ,

• ^a n , m + 2 , a n + 2, m , a n + 2, m + 2 в младших РДИ.

элементов по горизонтали и вертикали, восстанавливают элементы изображения a _{n , m} , a n, m + 2 , a n + 2, m , a n + 2, m + 2 с Учетом фоРмУл (1) и (2).

Если в двух верхних битах считанного файла приняты символы 10, то элементы a n _m + , a n + 1, m , a n + 1, m + 1 , a n + 1, m + 2 , a n + 2, m + 1 ^{( l} - 1 ) ^-го РДИ повторяют элементы l -го РДИ.

Если в двух верхних битах считанного файла приняты символы 01, то значения элемен- тов an, m+i, an+i, m, an+1, m+1, an+1, m+2 , an+2, m+1 (l — 1) -го РДИ противоположны зна чениям элементов l -го РДИ.

(a)

(б)

Рис. 8. Исходное (а) и восстановленное (б) изображение «Самолет»

Если в трех верхних разрядах файла приняты символы 000, то из 4-8 разрядов файла считывают значения элементов a n, _{m +} i , a _{n +} i, _m , a n + 1, m + 1 ^, a n + 1, m + 2 ^, a n + 2, m + 1 ^.

Если в трех верхних разрядах файла приняты символы 111, то считанные из 4-8 разрядов файла значения элементов ( l – 1)-го РДИ повторяются указанное количество раз.

На рис. 8 приведен пример четырехразрядного исходного и восстановленного изображения (768x512 элементов). Коэффициент сжатия представленного изображения равен 15,37.

Качество изображения в большей степени определяется точностью восстановления элементов в старших РДИ и незначительно зависит от потерь в младших РДИ. Поэтому степень сжатия можно увеличить, существенно не изменяя качество изображения, за счет внесения потерь в младшие РДИ. С этой целью был разработан алгоритм, в котором младшие РДИ (1-4 – для восьмиразрядного изображения), в отличие от основного алгоритма, кодируются следующим образом.

Если в анализируемой области ( l – 1)-го РДИ более трех элементов совпадают с элементами ( l – 1)-го РДИ, то значение счетчика повтора увеличивается.

А если в анализируемой области ( l – 1)-го РДИ более трех элементов переходят в противоположные относительно соответствующих элементов в l -ом РДИ, то увеличивается значение счетчика пропуска.

Возможный формат передаваемых данных для младших РДИ в модифицированном алгоритме показан на рис. 9.

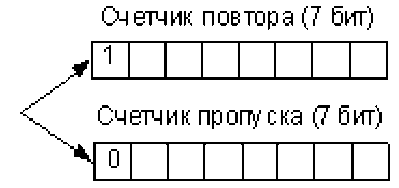
Рис. 9. Формат передаваемых данных младших РДИ в модифицированном алгоритме

В файле верхний бит отводится для передачи информации о передаваемых элементах, следующие семь бит – для значения счетчика. Счетчик может принимать значения от 1 до 128. Максимальный коэффициент сжатия (3) для модифицированного алгоритма равен 144.

На рис. 10 а,б приведен пример тестового восьмиразрядного исходного и восстановленного изображения (512x512 элементов) основным алгоритмом, а на рис. 11 увеличенный фрагмент исходноготестового изображения(а), восстановленного основным алгоритмом (б) и восстановленного модифицированным алгоритмом (в).

б)

Рис. 10. Исходное (а) и восстановленное основным алгоритмом тестовое изображение (б)

Из сравнения изображений на рис.8,10,11 следует: 1) при резких переходах цвета на исходном изображении - на восстановленном изображении возможны неровности границ. Это объясняется неточностью вычисления элементов изображения в РДИ при резких изменениях цвета; 2) при плавных изменениях цвета - восстановленное изображение практически полностью повторяет исходное; 3) использование модифицированного алгоритма позволяет увеличить коэффициент сжатия по сравнению с основным алгоритмом примерно в 1,5-2 раза без существенных изменений в качестве.

Выводы

Таким образом,разработанныйосновнойалго-ритм сжатия изображений имеет хорошее качество при среднем коэффициенте сжатия 9-10 – для четырехразрядных изображений и 3-5 – для восьмиразрядных изображений. Наиболее высокий коэффициент сжатия получен на изображениях с большими однородными областями. Увеличить коэффициент сжатия можно за счет внесения потерь в изображение, прежде всего в младшие РДИ, что несущественно отразится на качестве изображения.

Разработанный алгоритм прост в реализации и требует небольших вычислительных затрат.

Рис. 11. Увеличенный фрагмент: а) исходного изображения; б) восстановленного основным алгоритмом ( K _c =1,36); в) восстановленного модифицированным алгоритмом ( K _c =1,96)

Для определения элемента изображения требуются два умножения и одно сложение (1), (2), а также для сравнения элементов в соседних битовых РДИ – одно сложение по mod 2, что при умеренно больших размерах изображения вполне допустимо. Алгоритм может быть ориентирован для сжатия полутоновых и цветных изображений с большими областями повторяющегося цвета.