Разработка алгоритмов цифровой обработки изображений на основе метода Винограда в общем виде и анализ их вычислительной сложности

Цифровая обработка изображений широко используется в различных областях современной науки и техники [1]. Основой многих методов обработки изображений является многократное использование цифровой фильтрации, имеющей высокую вычислительную сложность. Устройства обработки изображений не поспевают за стремительным ростом количественных и качественных характеристик цифровых визуальных данных [2, 3]. Одной из самых активно решаемых задач современной науки является разработка и развитие методов и средств для улучшения качественных и эксплуатационных показателей устройств цифровой обработки изображений. Проработано множество подходов, в числе которых распараллеливание вычислений [4], использование различных аппаратных ускорителей [5] и так далее.

В данной статье рассмотрены методы цифровой фильтрации изображений. Различают фильтры нечетно- го и четного порядков, содержащие нечетное и четное количество коэффициентов соответственно. Цифровая фильтрация прямым методом при использовании фильтра нечетного порядка представима в виде

( r - 1)/ ² ( r - 1)/ ²

I 2 ( x,y ) = E E I i ( x + i,y + j ) R ( i,j ) , i =- ( r - ¹)/ 2j =- ( r - ¹)/²

где I1 и I2 – исходное и обработанное двумерные изображения соответственно; x и y – номера строки и столбца пикселя, обрабатываемого фильтром с маской R размера r × r. Цифровая фильтрация прямым методом при использовании фильтра четного порядка представима в виде r2r2

I 2 ( x , y ) = E E I i ( ^x + i , y + j ) R ( i , j ) .

i =- r / 2 + 1 j =- rl 2 + 1

Примерами фильтров нечетного и четного порядков являются фильтры сверточных слоев нейронной сети

• [6] и тензорные вейвлеты [7] соответственно. Схема цифровой фильтрации прямым методом представлена на рис. 1, где фильтр с маской R размера 3×3 используется для получения фрагмента M размера 1×1 из фрагмента N размера 3×3. Размер маски фильтра при использовании прямого метода совпадает с размером фрагментов, на которые делится исходное изображение для обработки.

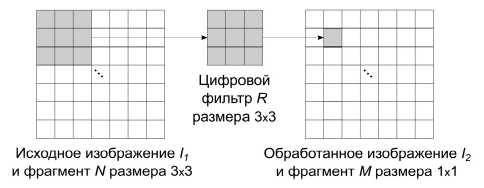
Рис. 1. Схема цифровой фильтрации прямым методом

В качестве современной альтернативы классическому прямому методу фильтрации используется метод Винограда [8], основанный на матричном умножении и позволяющий значительно снизить вычислительную сложность обработки изображений за счет групповой обработки пикселей. Обработанное изображение собирается не из совокупности отдельных пикселей, а из фрагментов некоторого размера, что позволяет уменьшить количество вычислительно сложных операций умножения за счет увеличения количества операций сложения. При этом качество обработки изображения остается неизменным [8]. Схема цифровой фильтрации методом Винограда представлена на рис. 2, где фильтр с маской R размера r × r используется для получения фрагмента M размера m × m из фрагмента N размера n × n , где n = m + r –1. Метод Винограда для фильтра R и фраг-

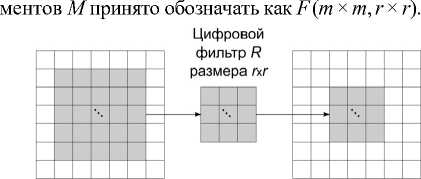
Исходное изображение /(          Обработанное изображение /2

и фрагмент N размера пхп         и фрагмент М размера mxm

Рис. 2. Схема цифровой фильтрации методом Винограда F (m × m, r × r)

Метод Винограда активно используется для снижения вычислительной сложности и повышения скорости работы различных алгоритмов нейросетевой обработки изображений [5]. В статье [9] предложенные алгоритмы цифровой фильтрации на основе метода Винограда для сверточных слоев нейронных сетей показали превосходство над быстрым преобразованием Фурье по скорости работы глубокой нейронной сети при обработке больших массивов визуальных данных. Данный подход был расширен и обобщен на случаи обработки одномерных, двумерных и трехмерных сигналов сверточной нейронной сетью [10]. На базе данных исследований разработаны различные архитектуры [11] и аппаратные ускорители [12– 14] для высокопроизводительной реализации алгоритмов нейросетевой обработки изображений на основе метода Винограда. В работе [15] предложена архитектура цифрового фильтра с использованием метода Винограда в системе остаточных классов, аппаратная реализация которого позволила повысить скорость обработки изображений за счет повышения аппаратных и энергетических затрат. Несмотря на активное применение, в каждой из изученных работ рассматриваются только один или несколько частных случаев использования метода Винограда F (m × m, r × r) для конкретных размера r × r цифрового фильтра и размера m × m фрагментов изображения. Алгоритмы обработки изображений на основе метода Винограда в общем виде еще не разработаны.

Целью данной работы является разработка алгоритмов обработки двумерных изображений на основе метода Винограда F ( m × m , r × r ) в общем виде для любых значений размера r × r маски фильтра R и размера m × m фрагментов M обработанного изображения, а также анализ вычислительной сложности этих алгоритмов и сравнение с прямым методом при использовании двумерных фильтров нечетного и четного порядков.

Дальнейшая часть статьи организована следующим образом. В параграфе 1 представлены разработанные алгоритмы метода Винограда для обработки изображений. В параграфе 2 проведен анализ вычислительной сложности алгоритмов при различных условиях их использования и сравнение с прямым методом. В заключении подведены итоги исследования и сделаны выводы. В приложении А представлены матрицы обработки изображений, полученные при использовании алгоритмов и примененные для анализа вычислительной сложности метода Винограда.

1.    Алгоритмы построения матриц преобразования для метода Винограда в общем виде

Фильтрация изображения методом Винограда в матричной форме имеет вид [8]

M = A T ( ( GRG T ) о ( B T NB ) ) A, (1)

где M – фрагмент обработанного изображения размера m × m ; R – маска фильтра размера r × r ; N – фрагмент исходного изображения размера n × n , где n = m + r –1; A^T , G , G^T , B^T , B , A – матрицы преобразования размеров m × n , n × r , r × n , n × n , n × m , m × m соответственно; ⊙ – оператор поэлементного умножения матриц. В обозначении метода Винограда F ( m × m , r × r ) указываются размер m × m фрагментов обработанного изображения и размер r × r маски фильтра, так как от них зависят размеры всех остальных матриц и фрагментов изображения.

Для составления матриц преобразования нужно выбрать n точек s 0 , s ₁ , ^ , s_{n -} 2 , s n _{- 1} , чтобы построить интерполяционный многочлен Лагранжа L [16]. На основе значений точек данного многочлена составляется матрица Вандермонда V [17] размера n × n , имеющая следующий общий вид

0 s0 s10 s02. C n-2 .. s0 C n-1 Л s0 510 s11 s12. c n-2 .. s1 c n-1 s1 V = s 20 ... s12 ... s22. ... . c n-2 .. s2 ..... c n-1 s2 ... 0 sn-2 sn-2 2 sn-2 . c n-2 ..   sn-2 c n-1 sn-2 ч 0 0 0. .. 0 1 y где значения элементов последней строки вычисляются как предел отношения к sn- при sn — i^ да.

Пример 1. Пусть выбраны n =6 точек s 0 =0, s 1 =1, s 2 =–1, s 3 =2, s 4 =–2, s 5 = ∞ для многочлена L . Тогда матрица V имеет вид

	( 1	0	0	0	0	0 1
	1	1	1	1	1	1
V =	1	- 1	1	- 1	1	- 1
	1	2	4	8	16	32
	1	- 2	4	- 8	16	- 32
	1 0	0	0	0	0	1 y

Далее по известным значениям r , m и n , а также по матрице V составляются матрицы преобразования A^T размера m × n , G размера n × r , B^T размера n × n . Для получения матрицы A^T выберем из матрицы V^T первые m строк и n столбцов. Заменив элемент, стоящий в последней строке и последнем столбце на 1, получим матрицу A^T . Процесс составления матрицы A^T представлен в виде алгоритма 1.

Алгоритм 1. Составление матрицы преобразования A^T для фильтрации изображений методом Винограда Входные данные: матрица Вандермонда V

Выходные данные: матрица преобразования A^T

• 1:    рассчитать V^T

• 2:    A T ( i , j )= V T ( i , j ), где i = 1, m и j = 1, n

• 3:    A^T ( m , n )= 1

Для получения матрицы G выберем из матрицы V первые n строк и r столбцов. Составим диагональную матрицу из наименьших общих кратных знаменателей элементов строк обратной транспонированной матрицы V. Разделим каждую строку матрицы, выбранной из V, на соответствующий отличный от нуля элемент диагональной матрицы. Заменив в полученной матрице элемент, стоящий в последней строке и последнем столбце, на 1, получим матрицу G. Вычисление знаменателей элементов строк матрицы реализуется с помощью операции den (x)

1, x e Z, q, x e Q \ Z,

где x – элемент матрицы, q – знаменатель элементов строки матрицы, Z – множество целых чисел, Q \ Z – множество рациональных чисел с исключением целых. Вычисление наименьшего общего кратного знаменателей элементов строк матрицы реализуется с помощью операции

LCM ( x ₁, x ₂,..., x i ) = LCM ( LCM ( x ₁, x ₂,..., x_i_ ₁ ) , x i ) .

Процесс составления матрицы G представлен в виде алгоритма 2.

Алгоритм 2. Составление матрицы преобразования G для фильтрации изображений методом Винограда Входные данные: матрица Вандермонда V

Выходные данные: матрица преобразования G

• 1:    рассчитать V ^–T

• 2:    для i от 1 до n

• 3:      для j от 1 до n

• 4:           y i = den ( V ^–T ( i , j ))

• 5:      конец

• 6:      z i = LCM { y i }

• 7:    конец

• 8:    G ( i , j )= V ( i , j )/ z i , где i = 1, n и j = 1, r

• 9:    G ( n , r )= 1

Для составления матрицы B^T построим диагональную матрицу из наименьших общих кратных знаменателей элементов строк обратной транспонированной матрицы V . Умножим каждую строку обратной транспонированной матрицы на соответствующий отличный от нуля элемент диагональной матрицы и получим матрицу B^T . Вычисление знаменателей элементов строк матрицы и их наименьшего общего кратного реализуется с помощью операций, описанных в алгоритме 2. Процесс составления матрицы B^T представлен в виде алгоритма 3.

Алгоритм 3. Составление матрицы преобразования B^T для фильтрации изображений методом Винограда Входные данные: матрица Вандермонда V

Выходные данные: матрица преобразования BT фрагментов 2×2 (m =2). В этом случае для обработки изображения его понадобится разделять на фрагменты размера 4×4 (n = m +r–1 =2 +3–1 =4). При использовании точек s0 =0, s1 = 1, s2 =–1, s3 = ∞ для построения многочлена L и составления матрицы V, матрицы преобразования AT, G и BT, составленные по алгоритмам 1–3, и их транспонированные версии A, GT и B имеют вид

Г 1      0 0 )

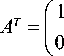
1 10 ) G = 12 12

1 - 1 1 J ,      12 — 12

BT

GT

_ч 0

- 1

- 1

- 1 0 '

1 0

1 0

Г 1

- 1

0 1 J

12 0 '

- 12 0

12 1

1 ^{0 1} J

Г 1 0

0 0 )

- 1

- 1

( 0 0

Матрицы преобразования A^T , G , B^T , A , G^T , B , составленные в примере 2 с использованием алгоритмов 1–3 для случая F (2 × 2,3 × 3), имеют широкое практическое применение, что подтверждается их использованием при проведении исследований в работах [9, 11, 12, 18]. Системы обработки изображений используют множество различных фильтров для обработки изображений разного размера. В результате размеры фрагментов исходного и обработанного изображения могут варьироваться в зависимости от конкретных параметров системы. Элементы матриц преобразования, помимо перечисленного, зависят еще и от выбора точек многочлена Лагранжа. Все указанные факты и закономерности влияют на вычислительную сложность обработки изображений. Далее представлены результаты анализа вычислительной сложности метода Винограда при обработке изображения масками фильтров разного размера, с использованием различных размеров фрагментов исходного и обработанного изображений и нескольких наборов точек многочлена Лагранжа для составления матрицы Вандермонда и матриц преобразования.

2. Анализ вычислительной сложности цифровой фильтрации изображений методом Винограда

Вычислительная сложность цифровой фильтрации изображений методом Винограда F ( m × m , r × r ) в основном зависит от значений r и m , определяющих количество элементов матриц, а следовательно, и число необходимых умножений и сложений. Однако еще одним важным фактором является выбор значений точек 5 о , 5 1 , ^ , s n _{— 2} , s n -i , так как на их основе строятся все используемые матрицы преобразования. В данной

статье рассмотрены случаи обработки изображений с разными размерами m × m ( m =2, 3,4, 5) обрабатываемых фрагментов и масок фильтра r × r ( r =3,4) при использовании трех наборов точек многочлена Лагранжа L для построения матриц Вандермонда V . Наборы точек и матрицы преобразования A^T , G , B^T , построенные с использованием алгоритмов 1–3, представлены в приложении А и могут быть использованы для разработки методов и алгоритмов обработки изображений на основе метода Винограда. На основе полученных матриц преобразования составлена табл. 1, содержащая результаты подсчета количества умножений и сложений, необходимых для цифровой фильтрации изображений прямым методом и методом Винограда для всех рассмотренных случаев. Количество умножений для каждого фрагмента в таблице рассчитано следующим образом.

• 1.    При использовании прямого метода количество умножений, необходимых для получения фрагмента обработанного изображения, равно числу r ² коэффициентов фильтра, так как размер фрагмента исходного изображения совпадает с размером используемого фильтра. Например, при обработке изображения фильтром размера 3 × 3 мы используем фрагменты изображения аналогичного размера и умножаем 3² =9 значений яркости пикселей на 9 соответствующих коэффициентов фильтра.

• 2.    При использовании метода Винограда количество умножений, необходимых для получения фрагмента обработанного изображения, равно числу пикселей n ² фрагмента исходного изображения, так как матричное умножение GRG^T в формуле (1) выполняется предварительно при известных значениях коэффициентов фильтров, и результат данного умножения, как и матрицы преобразования A^T , B^T , A , B , хранится в памяти устройства в виде констант, а умножение на константу сводится к масштабированию и сложению. Например, для умножения числа на константу 5, имеющую в двоичной системе счисления вид 101 2 , нужно масштабировать это число на два бита влево и сложить с исходным числом. Масштабирование чисел не требует значимых вычислительных ресурсов для своего выполнения. Таким образом все умножения матриц, кроме поэлементного, реализуются с помощью сложений, а поэлементное умножение выполняется единожды для двух матриц размера n × n . Например, при обработке изображения методом Винограда F (2 × 2,3 × 3) исходное изображение делится на фрагменты размера 4 × 4 и количество умножений для получения одного фрагмента обработанного изображения равно 4² = 16.

• 2.    При использовании метода Винограда количество основных сложений, необходимых для получения фрагмента обработанного изображения, равно сумме числа сложений ненулевых элементов матрицы по строкам, умноженной на сумму числа строк и столбцов этой матрицы по матрицам преобразования A^T и B^T , так как в формуле (1) данные матрицы являются первыми множителями, а их транспонированные версии B и A – вторыми. В примере 2 при обработке изображения методом Винограда F (2 × 2,3 × 3) в каждой из строк матрицы A^T размера 2× 4 по три ненулевых элемента и для каждой из этих строк нужно по два суммирования, а в каждой из строк матрицы B^T размера 4 × 4 по два ненулевых элемента и для каждой из этих строк нужно по одному суммированию, поэтому количество основных сложений равно (2+2) (2+4) +(1+1+1+1)(4+4) =56.

• 3.    При использовании метода Винограда количество дополнительных сложений, необходимых для получения фрагмента обработанного изображения, равно количеству единиц элемента матрицы в его двоичной записи, уменьшенному на единицу и умноженному на сумму числа строк и столбцов этой матрицы по каждому ненулевому элементу матриц A^T и B^T , отличному от степени двойки без учета знака. В случае 2 из приложения А, при обработке изображения методом Винограда F (3 × 3,3 × 3) в матрице B^T имеется один ненулевой элемент 3, отличный от степени двойки. В двоичной записи этого числа присутствует две единицы 3 = 11 2 , следовательно, оно требует одной дополнительной операции сложения при каждом использовании. Данное число будет использоваться 5 +5 раз (сумма числа строк и столбцов матрицы B^T ), поэтому количество дополнительных сложений равно 1 ⋅ (5 +5)= 10.

• 4.    Общее количество сложений равно сумме количества основных и дополнительных сложений.

Количество сложений для каждого фрагмента в таблице рассчитано следующим образом.

1. При использовании прямого метода количество сложений, необходимых для получения фрагмента обработанного изображения, равно числу умножений, уменьшенному на единицу. Например,

при обработке изображения фильтром размера 3 × 3 мы умножаем 32 =9 значений яркости пикселей на 9 соответствующих коэффициентов фильтра и складываем полученный результат с использованием 9– 1 = 8 сложений. При этом дополнительных сложений не требуется, так что общее число сложений равно числу основных сложений.

При использовании метода Винограда мы получаем на выходе не значение яркости одного пикселя, а набор значений яркости группы пикселей, принадлежащих фрагменту размера m × m. Некорректно говорить о количестве умножений и сложений, необходимых для обработки одного отдельно взятого пикселя, так как для расчета значения его яркости нужно обработать весь фрагмент целиком. В то же время фрагменты обработанного изображения при использовании прямого метода всегда имеют размер 1 × 1. Для корректного сравнения вычислительной сложности прямого метода и метода Винограда в рамках данной статьи введем понятие удельного веса пикселя обрабо- танного изображения, вычисляемого делением количества операций (умножений или сложений), необходимых для получения фрагмента обработанного изображения, на количество пикселей m2 данного фрагмента. В примере 2 при обработке изображения методом Винограда F (2 × 2,3 × 3) количество умножений для получения одного фрагмента обработанного изображения 42 =16, а число пикселей фрагмента 2× 2 обработанного изображения 22 =4, тогда удельный вес пикселя по умножениям равен 16/4=4.

Для оценки времени работы микроэлектронного устройства, реализующего цифровую обработку изображений, воспользуемся методикой, основанной на подсчете количества срабатываний базовых логических элементов «и», «или» [19]. Время срабатывания одного такого элемента будем считать условной единицей (у.е.). В соответствии с этой методикой время выполнения умножения и сложения двух k -битных чисел на современных устройствах вычислительной техники при использовании для сложений одного из самых быстрых сумматоров, а именно Kogge-Stone adders (KSA) [20], а для умножений бинарного дерева из KSA без ускоряющих техник (например, деревьев Уоллеса и Дадда [21]), равно 8,8 log 2 k +5 и 2 log 2 k +4 [22] соответственно. Сравним время выполнения фильтрации при использовании прямого метода и метода Винограда на основе значений удельных весов пикселя по умножениям и сложениям, представленных в табл. 1. Например, время обработки изображения методом Винограда F (2 × 2,3 × 3) с удельными весами пикселя по умножениям и сложениям 4 и 14 соответственно будет равно 4 ⋅ (8,8 log 2 k +5)+ 14 ⋅ (2log 2 k +4) =63,2log 2 k +76. При обработке изображений с глубиной цветовых каналов, равной 8, цифровым фильтром с 8-битными коэффициентами получим 63,2 log 2 8 +76 = 265,6. Изображения с 8-битными цветовыми каналами являются наиболее распространенными и получаемыми с использованием мобильных устройств и цифровых фотоаппаратов. Результаты расчета времени фильтрации изображений при использовании прямого метода и метода Винограда представлены в табл. 2, получены с допущениями и требуют проверки на современных устройствах вычислительной техники, таких как программируемые пользователем вентильные матрицы (field-programmable gate arrays, FPGAs) и интегральные схемы специального назначения (application-specific integrated circuits, ASICs).

На основе полученных результатов, представленных в табл. 1 и 2, сделаны следующие выводы.

• 1.    Использование метода Винограда позволило уменьшить вычислительную сложность цифровой фильтрации изображений асимптотически от 55,56% до 84,00% по сравнению с прямым методом, в зависимости от размеров фильтра и фрагментов изображения, а также выбранного многочлена Лагранжа. При этом качество обработки изображения осталось неизменным.

  Табл. 1. Количество умножений и сложений при обработке изображений прямым методом и методом Винограда для различных фильтров, различных фрагментов изображения и различных наборов точек многочлена Лагранжа

  H ^ 3 e	d 0 H s	£ s 5 | * Я ” x 5 S g S §1 »«f 0	3 « © 3 «	Для каждого фрагмента				Удельный вес пикселя
  				3 3 3 3 S	Сложения			3 3 3 3 S	Сложения
  					3 ^ о ”	§ ^ а ё " «	9 9 м		§ а 3 о ”	§ ^ а ё " *	9 9 м
  Фильтр нечетного порядка размера 3× 3	Прямой	1	–	9	8	0	8	9,00	8,00	0,00	8,00
  	F (2×2,3×3)	4	L 1 , L 2 , L 3	16	56	0	56	4,00	14,00	0,00	14,00
  	F (3×3,3×3)	9	L 1 , L 2 , L 3	25	174	10	184	2,78	19,33	1,11	20,44
  	F (4×4,3×3)	16	L 1 , L 2 , L 3	64	332	24	356	2,25	20,75	1,50	22,25
  Фильтр четного порядка размера 4× 4	Прямой	1	–	16	15	0	15	16,00	15,00	0,00	15,00
  	F (2×2,4×4)	4	L 1 , L 2 , L 3	25	138	10	148	6,25	34,50	2,50	37,00
  	F (3×3,4×4)	9	L 1 , L 2 , L 3	36	291	24	315	4,00	32,33	2,67	35,00
  	F (4×4,4×4)	16	L 1	49	590	391	981	3,06	36,88	24,44	61,31
  			L 2 , L 3	49	576	196	772	3,06	36,00	12,25	48,25
  	F (5×5,4×4)	25	L 1	64	927	854	1781	2,56	37,08	34,16	71,24
  			L 2 , L 3	64	927	320	1247	2,56	37,08	12,80	49,88

  
  

  Табл. 2. Время фильтрации изображений прямым методом и методом Винограда для различных фильтров, различных фрагментов изображения и различных наборов точек многочлена Лагранжа

  Размер фильтра	Метод	Многочлен Лагранжа	Время выполнения фильтрации, у.е.
  			В общем случае	При к = 8
  3×3	Прямой	–	95,2log 2 k +67	352,60
  	F (2×2,3×3)	L 1 , L 2 , L 3	63,2log 2 k +76	265,60
  	F (3×3,3×3)	L 1 , L 2 , L 3	65,34log 2 k +95,66	291,68
  	F (4×4,3×3)	L 1 , L 2 , L 3	64,3log 2 k + 100,25	293,15
  4×4	Прямой	–	170,8log 2 k +140	652,40
  	F (2×2,4×4)	L 1 , L 2 , L 3	129log 2 k + 179,25	566,25
  	F (3×3,4×4)	L 1 , L 2 , L 3	105,2log 2 k + 160	475,60
  	F (4×4,4×4)	L 1	149,55log 2 k +260,54	709,19
  		L 2 , L 3	123,43log 2 k +208,3	578,59
  	F (5×5,4×4)	L 1	165,01log 2 k +297,76	792,79
  		L 2 , L 3	122,29log 2 k +212,32	579,19

  
  

• 2.    При этом время обработки изображения с глубиной цветовых каналов, равной 8, цифровым фильтром с 8-битными коэффициентами сократилось до 27,10%. Для обоих рассмотренных фильтров наибольшее сокращение времени достигнуто при использовании фрагментов обработанного изображения размера на единицу меньше, нежели размер маски соответствующего фильтра, то есть для случаев F (2×2,3×3) и F (3×3,4×4).

• 3.    Чем больше размер фрагментов изображения, тем меньше удельный вес пикселя по умножениям при цифровой фильтрации методом Винограда. При обработке фрагментов большого размера размер фильтра будет мал по отношению к ним, в результате чего удельный вес пикселя по умножениям будет немногим больше единицы. Например, при использовании фильтра размера 4 × 4 для обработки изображения с получаемыми на выходе фрагментами размеров 32 × 32 и 6 4 × 64 , количество умножений будет 1,20 и 1,10 соответственно, в то время как прямой метод требует 16 умножений.

• 4.    Четность порядка фильтра не оказывает значимого влияния на вычислительную сложность используемых методов цифровой фильтрации, в отличие от размера маски фильтра при его использовании для обработки фраг мен тов исходного изображения размера n * n, где n = 3,8.

• 5.    Использование точек 5 0 , 5 1 ,..., s_{n -} 2 , s n _-1 со значениями, отличными от степеней двойки, для построения интерполяционного многочлена Лагранжа L и составления матрицы Вандермонда V приводит к значительному увеличению числа дополнительных суммирований и увеличению вычислительной сложности метода Винограда.

• 6.    Использование отрицательных степеней двойки в качестве значений точек s о , s i , _ , s „ — 2 , s „ —1 приводит к значительному увеличению числа масштабирований и усложняет проектирование устройств обработки изображений на основе метода Винограда.

Обобщая вышесказанное, использование метода Винограда позволяет значительно уменьшить вычислительную сложность методов цифровой обработки изображений. При этом матрицы преобразования метода Винограда могут быть составлены с использованием разработанных алгоритмов 1–3 для любых: размера двумерного изображения; размера его фрагментов; размера и порядка маски двумерного фильтра. Составленные матрицы преобразования AT, G, BT, представленные в приложении А, могут быть использованы для разработки методов и алгоритмов обработки изображений на основе метода Винограда. Чем больше размер фрагментов изображения, тем выше эффективность метода Винограда. Выбор точек со значениями степеней двойки и противоположными им числами для построения многочлена Лагранжа L и составления матрицы Вандермонда V позволяет минимизировать количество дополнительных суммирований и уменьшить вычислительную сложность обработки изображений.

Перспективным направлением дальнейших исследований является аппаратная реализация разработанных алгоритмов на FPGA и ASIC, разработка алгоритмов цифровой обработки изображений на основе метода Винограда в общем виде для одномерных вейвлет-фильтров с децимацией и для свертки с шагом, используемой в сверточных нейронных сетях.

Заключение

Разработаны алгоритмы цифровой обработки двумерных изображений на основе метода Винограда в общем виде. Анализ полученных результатов показал, что использование метода Винограда сокращает вычислительную сложность цифровой фильтрации до 84% по сравнению с традиционным прямым методом в зависимости от параметров фильтра и фрагментов изображения, не влияя при этом на качество обработки изображения. Составленные матрицы преобразования метода Винограда и разработанные алгоритмы могут быть использованы в системах обработки изображений для улучшения эксплуатационных характеристик современных микроэлектронных устройств, осуществляющих очистку от шума и сжатие изображений, а также распознавание образов. Перспективным направлением дальнейших исследований является аппаратная реализация разработанных алгоритмов на FPGA и ASIC, разработка алгоритмов цифровой обработки изображений на основе метода Винограда в общем виде для одномерных вейвлет-фильтров с децимацией и для свертки с шагом, используемой в сверточных нейронных сетях.