Разработка алгоритмов трёхмерной реконструкции кристаллической решётки по изображениям проекций

исследование разработанных алгоритмов при помощи метрик сравнения изображений.

МОДЕЛИРОВАНИЕ ИДЕАЛЬНОЙ КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ

Модель кристаллической решётки может быть описана решёткой Браве. Исчерпывающим описанием решётки Браве является элементарная ячейка, представимая в виде трёх некомпланарных векторов трансляции [9]. В кристаллографии для определения векторов трансляции используют длины векторов a , b , c , и углы между векторами а, в, Y. Дополнительно в качестве исходных параметров для моделирования множества узлов кристаллической решётки определим начальные и конечные индексы узлов по каждой оси I0, J0 иK0, I1, J1 и K1 .

Для построения модели кристаллической решётки необходимо знать векторы трансляции [10]. Разработанный метод позволяет вычислить векторы трансляции по параметрам, принятым

в

кристаллографии и заключается в следующем:

Вычисляем угол ^ :

cos у - cos а cos в sin а sin в

£ = arccos

, где а, р, Y - углы векторов трансляции.

Масштабируем вектор c следующим способом:

С = ( о, Н 1,0 )

.

I ----►

Находим промежуточные векторы f и g :

f = | а ||sin в ( 1 0 0 ) ;

Р = н Н

g = b sin а ( cos £ 0 sin £ ) .

Находим векторы p ₁ и p ₂ :

cos в = ( 0 1 0)|| а | |cos в ;

b ||cos а = ( 0 1 0 )|| а | |cos в .

—— ——

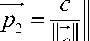
Вычисляем искомые векторы а и b :

а = 7+Р;

—— I I ^b = g ⁺ Р 2 .

Зная векторы трансляции , можем сгенери ровать множество точек , соответствующих кри сталлической решётке . Это можем сделать , указав диапазон изменения целых чисел I ₀ , J ₀ , K ₀ и I ₁ , J ₁ , K ₁ . Тогда в цикле данная операция будет выглядеть следующим образом :

for i = 1 ₀: 1 1

for j = J 0 ^: J 1

for k = K ₀: K 1

T, = ia + jb + kc ijk .

Из геометрии элементарной ячейки углы а , р , у могут принимать не любые значения . При углах а >  п и р >  п наблюдается симметричная картина. Соответственно, углы следует ограничить в диапазонах: а е ( 0, п ) , в е ( 0, п ) . Третий угол ограничивается в диапазоне:

у е{ф : cos фе (cos(а + в), cos(а - в) )}п( 0, п)

.

Такое ограничение представимо в виде (1 ).

у е [ min ( а 1 , а ₂ ) ,max ( а 1 , а ₂ ) ] ,    (1)

где а1 =({2п-(а + в)}^{а +в})п( 0, п ), а 2 = [а - в

.

Условие (1) ограничивает угол у на отрезке, что позволяет сгенерировать случайную решётку по заданным параметрам, принятым в кристаллографии.

Разработанный метод позволяет генерировать трёхмерное множество узлов, представляющее собой решётку Браве [9]. На практике метод полезно применять для исследования большого набора кристаллических решёток. Набор генерируется автоматически, и выявляются решётки, с которыми алгоритм работает некачественно.

АЛГОРИТМЫ РЕКОНСТРУКЦИИ

МНОЖЕСТВА УЗЛОВ КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ

Алгоритм обратного проецирования – процесс, обратный алгоритму проецирования трёх- мерного изображения на плоскости. Для анализа и оценки его работоспособности необходимо иметь набор идеальных кристаллических решёток и их проекций. По степени схожести эталонной решётки и полученной в результате обратного проецирования можно оценивать качество работы алгоритма. В настоящей работе рассматриваются алгоритмы обратного проецирования, позволяющие восстанавливать трёхмерную структуру кристаллической решётки по плоским изображениям, ориентированным в пространстве.

Алгоритм реконструкции в качестве входных данных получает изображения проекций и их положение в пространстве. Результатом работы алгоритма является некоторое трёхмерное изображение, представляющее собой набор точек в пространстве или, выражаясь математически, конечное множество точек трёхмерного пространства.

Существует множество способов реконструкции трёхмерной структуры. Алгоритм компьютерной томографии решает общую задачу. При этом алгоритм имеет теоретическое обоснование сходимости [11]. Этот алгоритм может быть модифицирован до более простых случаев, таких как восстановление конечного множества узлов. В модифицированных алгоритмах суммарное изображение аппроксимируется при помощи иных подходов. В работе разработаны два алгоритма реконструкции, позволяющих восстановить конечное множество узлов решётки: алгоритм, основанный на сеточном разбиении прямой, и алгоритм, основанный на минимизации расстояния.

Основная задача алгоритмов реконструкции – восстановить изображение, чтобы суммарное изображение приближенно удовлетворяло выражению:

s (x )«Х R- (A (Ф k) x).

k где A(Ф) - матрица преобразования в базис проекции,

R – лучевое преобразование.

В алгоритмах реконструкции условимся рассматривать бинарные изображения на проекциях, то есть выражения вида (2).

R ф ( z ) =

1, z Е Q <                      ,

0, z ^Q

где Q - некоторая область на проекции,

Ф - матрица, задающая проецирующее преобразование, z е^2 - вектор.

С учетом того, что изображения на проекциях бинарны, а восстанавливаемое «изображение» представляют собой конечное множество точек, можем полагать, что 7 ( x ) = F [ ^s ( x ) [ , где F -какой-либо фильтр или обрабатывающий множество алгоритм. В суммарном изображении узлы представляют собой «облака», или подмножества.

Восстановленное множество представляет собой некоторое распределение вероятностей. С учетом этого множество может быть подвержено фильтрации. Множество, полученное в результате фильтрации, будет представлять собой конечную оценку исходного множества. В работе был применён фильтр, основанный на алгоритме кластеризации, выделяющим «облака» точек.

Первый алгоритм обратного проецирования, основанный на сеточном разбиении прямой, описывается следующей процедурой действий:

• 1)    Выбираем основную проекцию.

• 2)    Для каждой ненулевой точки (т.е. точки принадлежащей узлу кристаллической решётки) на этой проекции:

• a)    определяется прямая, перпендикулярная к проекции и проходящая через эту точку;

• b)    вычисляется функцию u ( x ) - пока -зывающая количество проекций, на которых проекция прямой пересекает узлы решётки u ( x ) = { к : R_k (ф_кx ) >  0 л к = 1,..., i - 1, i + 1,..., n }| , x e X ..

Алгоритм обладает рядом недостатков. Дискретизация прямой приводит к неточности алгоритма, а уменьшение шага дискретизации влияет на скорость работы алгоритма.

Второй алгоритм устраняет указанные недостатки. Суть его работы в следующем:

• 1)    Выбираем основную проекцию.

• 2)    Переводим все ненулевые двумерные точки каждой проекции в пространство.

• 3)    Для каждой точки из проекции, взятой за опору:

• a)    Вычисляем значения t_i , участвующих в параметрическом задании прямой для точек на остальных проекциях по формуле

(I           I               I           I                        I               II \ n,x0)(n,n0)-(x0 -x,n0 )

.

■'            (I |n-||2-(n, nI )2)■

• b)    Вычисляем точку, которая может быть вос-I                             II

становлена в пространстве x ' = n ₀ t + x 0 .

• c)    Вычисляем расстояние

d2 =| x - xf -(n, ?)2, которое является минимальным расстоянием от точки на проекции до точки, которая может быть спроецирована на проекцию из всех возможных.

• d)    Если выполняется условие: d ² <  s ² , то точка в пространстве восстанавливается.

• e)    При этом, если параметры t i и t i _{+ 1} оказались с некоторой точностью равны, то, значит, восстанавливаемая точка уже была рассчитана ранее и попала еще в одну проекцию.

Алгоритм работает с точками ненулевой интенсивности, что позволяет повысить скорость восстановления кристаллической решётки. За счёт аналитического вычисления восстанавли- ваемых точек алгоритм обладает большей точностью, чем первый.

МЕТРИКИ СРАВНЕНИЯ МНОЖЕСТВ ПРОСТРАНСТВЕННЫХ ТОЧЕК

Обозначим через E и F два непустых компактных подмножества Rⁿ . Хаусдорфово расстояние между E и F можно задать несколькими способами [12]. В функциональном анализе часто рассматривают определение, связанное с окрестностью точки в виде открытого или замкнутого шара.

Пусть B r ( x ) - замкнутый шар, представляющий собой множество { y : d ( x , y ) <  r } . Для произвольного множества E из пространства R n и радиуса r >  0 дилатацией E радиуса r (обозначается E + r ) будем называть следующее выражение:

E + r = U {Br (x)' x e E}.

Пусть E и F – непустые компактные подмножества Rⁿ . Расстояние Хаусдорфа [12] между E и F :

H (E, F) = min {s > 0: Hs (E, F)} , где Hs (E, F ) = E c F + s л F c E + s.

Этому определению эквивалентно другое определение. Пусть E и F – непустые компактные подмножества Rⁿ . Расстояние Хаусдорфа между E и F будет определяться по формуле:

H ( E , F ) = max { d ( E , F ) , d ( F , E ) }

, где d (E, F ) = sup inf d (x, y).

x e X ^{y e Y}

Для того, чтобы вычислить метрику Хаусдорфа для конечных множеств, достаточно произвести вычисления по формуле:

H ( E , F ) = max { d ( E , F ) , d ( F , E ) }

, где d(E,F) = max min d(xi,ys).

• ^{v }} i : x i e E j :y j e F

Помимо метрики Хаусдорфа была проанализирована метрика, основанная на кватернионных сигналах.

Первичное аналитическое описание пространственного объекта [13] представляет собой кватернионный сигнал, имеющий следующий вид:

Q={q(n )}0, n-1 =ix (n)+jy(n)+kz (n), n = 0,1,..., N -1

, где N – количество отсчетов, задающих объект.

Кватернионный сигнал, представляющий собой проекцию на сферу сигнала Q , имеет вид:

Р =            = ix (n) + jy(n) + kz (n)

{p( )}0,N-1 x2 (n) + y2 (n) + z2 (n) , n = 0,1,..., N -1

где N – количество отсчетов.

В качестве проецирующих функций были выбраны полиномиальные отображающие функции гиперкомплексного переменного вида

M - 1

^m q nm p n , m = 0

где M — 1 - степень полинома, am – коэффициенты полинома (также являющиеся кватернионами), задающие отображение пространственной фигуры на сферу;

Коэффициенты полинома a_m могут быть найдены с помощью метода наименьших квадратов. Решая задачу минимизации общей погрешности аппроксимации, получаем систему линейных кватернионных уравнений, записываемую в виде: qa = p

N—1              N —1 где qr,m = £ qnqm , pr = £qnp, r = 0,1,...,M—1.

n = 0                   n = 0

Система решается непосредственно методом Гаусса или сводится к решению системы уравнений с действительными коэффициентами [13].

В качестве величины, характеризующей меру схожести объектов, может выступать результат скалярного произведения коэффициентов проецирующего полинома эталонного и обрабатываемого объектов, определяемого по формуле:

M — 1

E *( 3 ) a m a m. ) .

m = 0

Определение принадлежности исследуемой кристаллической решётки к тому или иному типу решёток Браве осуществляется путём сравнения полученных данных с эталонными: найденными ранее или теоретически смоделированными [14]. Метрика сравнения позволяет охарактеризовать степень схожести множеств. Множества будут считаться идентичными в случае удовлетворения меры схожести некоторому условию. При исследовании алгоритмов реконструкции будем анализировать само значение метрики сравнения. При этом качество работы алгоритма определяется мерой схожести эталонного множества и полученного в результате вычислений.

ИССЛЕДОВАНИЕ АЛГОРИТМОВ РЕКОНСТРУКЦИИ

Для проведения экспериментов разработан метод моделирования множества узлов идеальной кристаллической решётки, являющегося эталонным множеством. Множество проецируется на плоскости проекций, затем выполняется алгоритм реконструкции. Результирующее множество сравнивается с эталонным при помощи метрики сравнения. По результатам эксперимента можно делать выводы о качестве работы алгоритма.

Результатом алгоритма обратного проецирования определим «псевдо-изображение». Каждый узел восстановленной решётки имеет псевдоцвет, то есть цвет, соответствующий количеству проекций, в которые узел может быть спроецирован [15].

На рис. 1 приведены результаты реконструкции первым и вторым алгоритмами на примере триклинной решётки. Синий цвет соответствует узлу, который попадает в две проекции из трёх, а красный – во все три проекции.

На рис. 1б заметна неточность алгоритма, проявляющаяся в том, что узел сетки «промахнулся» мимо точки на проекции [15]. Поэтому алгоритм для трех восстановленных узлов указал, что они попали лишь в две проекции (синего цвета). Алгоритм, основанный на сеточном разбиении прямой, восстановил все узлы корректно (Рис. 1в).

Используемый фильтр, основанный на алгоритме кластеризации, хорошо работает на примерах решёток, в которых обнаруживаются частые скопления (облака) узлов. На рисунке 2 представлен результат работы алгоритма кластеризации на примере триклинной решетки.

Проанализируем два первых алгоритма на всех сингониях примитивных решёток с использованием обеих метрик, рассмотренных в данной работе (табл. 1).

Сравнивая результаты первого и второго столбцов с метрикой Хаусдорфа, третьего и четвертого столбцов с метрикой кватернионных сигналов табл. 1, можем убедиться, что второй алгоритм восстанавливает изображение точнее,

a)

Рис. 1. Сравнение работы алгоритмов реконструкции: а – эталонное изображение;

б – восстановленное изображение посредством алгоритма, основанного на сеточном разбиении; в – восстановленное изображение посредством алгоритма, основанного на минимизации расстояния

• а)                                                                 б)

Рис. 2. Результат обработки изображения посредством фильтра, основанного на алгоритме кластеризации: а – восстановленное изображение алгоритмом реконструкции; б – обработанное изображение

Таблица 1. Исследование алгоритмов реконструкции

Сингония примитивной решетки Метрика Хаусдорфа Метрика кватернионных сигналов Алгоритм, основанный на сеточном разбиении Алгоритм, основанный на поиске минимального расстояния Алгоритм, основанный на сеточном разбиении Алгоритм, основанный на поиске минимального расстояния Кубическая 0,100 0,000 0,0007 0,0000 Тетрагональная 0,100 0,000 0,0008 0,0000 Гексагональная 1,001 1,001 0,0008 0,0003 Тригональная 0,480 0,480 0,0007 0,0002 Ромбическая 0,100 0,000 0,0010 0,0001 Моноклинная 1,870 0,751 0,0007 0,0003 Триклинная 0,110 0,107 0,0005 0,0002 нежели первый. Обе метрики в целом показывают меньшее значение для случая второго алгоритма.

Алгоритм, основанный на поиске минимального расстояния, качественнее справляется с задачей реконструкции множества узлов кристаллической решётки. Алгоритм в результате восстанавливает все узлы из проекций, в отличие от алгоритма, основанного на сеточном разбиении прямой.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ

В результате проведенных исследований было показано, что алгоритм, основанный на минимизации расстояния, реконструирует структуру решётки точнее, чем алгоритм, основанный на сеточном разбиении прямой. Алгоритмы реконструкции могут применяться для восстановления трёхмерных моделей кристаллических решеток. Модификации процедур восстановления в ряде случаев позволяют увеличить точность реконструкции объекта. Кристаллическая решетка, являясь, по сути, множеством узлов, хорошо сочетается с алгоритмами, работающими с множеством точек, а не с сетками прямых.

Методы трёхмерной реконструкции кристаллических решеток по проекциям позволяют получать изображения решеток для их дальнейшего исследования. Качество алгоритма может определяться не только точностью и скоростью работы, но также и устойчивостью к шумам и случайным трансформациям эталонной кристаллической решетки.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках реализации мероприятий Программы повышения конкурентоспособности СГАУ среди ведущих мировых научно-образовательных центров на 2013–2020 годы; грантов РФФИ 14-01-00369-а, 14-07-97040-р_поволжье_а; программы № 6 фундаментальных исследований ОНИТ РАН «Биоинформатика, современные информационные технологии и математические методы в медицине» 2015 г.