Разработка аналитической модели шумозащитного экрана транспортных потоков

В качестве теоретической модели абсорбента, или диссипативной системы, может рассматриваться "структура Релея”, в которой, с одной стороны можно конструктивно совместить параметры собственно абсорбента, а с другой - минимальное сопротивление аэродинамическому потоку. Оригинальность постановки задачи заключается в представлении структуры в виде звукоизолирующей продуваемой преграды, а не чисто абсорбента. Резонансные явления в пористых структурах могут разделяться на резонансы микроструктур и макроструктур в сравнении с длиной волны падающего звука. Этот факт позволяет считать, что структура обеспечивает частотно-независимое звукопоглощение. Такое допущение возможно, если канал в структуре Релея рассматривать как недиспергирующий волновод, то есть /к=const, где - круговая частота, рад. с, k - волновое число, (k=2 / , рад/м).

Рассмотрим распространение звуковой волны в прямоточных каналах с учетом сопротивления среды. Канал заполнен воздухом, а направление распространения звуковой волны совпадает с направлением оси трубки.

Тогда уравнение движения вязкого газа в отдельном канале можно записать в следующем виде

P

-— = р

x

P

----= Р с t      0C0

где:   P ( X , t )

V

V ² t 2 d

2 V

x

-

.

избыточное давление в

звуковой волне; V ( x , t ) - усредненная

по сечению канала скорость частиц; x , t

- текущие координаты и время; -плотность воздуха; c - скорость звука;

- коэффициент сопротивления; d - диа-

метр канала.

Система уравнений (1) является нелинейной, интегрирование ее затруднено. система уравнений является гидродинамической моделью. В этой связи,

введем соответствующие параметры. Коэффициент определяется по фор-

64         Р Vd муле 5 - — (Re = ——

Re          Л

- динамиче-

ский коэффициент вязкости) (2)

Представление     в виде (2)

справедливо для 0 <  Re < 2300 ,что всегда выполняется в задачах линейной акустики. Тогда нелинейный член, содержащийся в (1), представим как

V 2     6432

V2          V .(3)

2d 2d2 Vd

Введем обозначение d2

тогда, заменив квадратичный закон сопротивления линейным, получим:

P — = p

x

P

---= P c t     0C

V

2 aV t

2 V

x

.

Решаем уравнение (15), найдем, при следующих начальных и граничных условиях:

P(x,t)|    = ^(t) , x0

Для пакета капилляров уравнение непрерывности можно записать в

P ( x , t

а р ( x, t)

t

x 0

P    C2V виде:              0

t     hx

где h - коэффициент пористости образца, равный отношению объема пор к общему объему. Введение коэффициента h оправдано физическими соображениями. Действительно, при заданном

градиенте

---- ,---, в пористом ма- x        t

Граничные условия (16) означают, что на поверхность пакета падает звуковая волна в виде единичной волны Хевисайда. Решение задачи для любого профиля волны можно получить, используя интеграл Дюамеля. Начальные условия (17) характеризуют состояние покоя во всех точках среды до прихода звуковой волны. К левой и правой частям применим преобразование Лапласа:

териале пор будет в 1/ h раз будет больше, чем в свободном воздухе.

Уравнение движения воздуха, заключенного в пористом материале:

P ( x ,^) = [

e st * P ( x , t ) dt ,     (18)

где s

-

dp X p

x     h

V

2 aV a t

-

струк-

комплексный параметр

С учетом начальных условий

турная постоянная, всегда > 1) (6) Дифференцируя по t и x ,

h ² P

2 _V

₀ c ₀

_h    2 _P

0 x где V(x,t)

;

t2x t

^{2 ah} ₂    ^{P         V} , (7,8)

О г* U t       U tU v

0c0 tt x и производные непрерывны:

V

(17), для изображения получим обыкновенное дифференциальное уравнение второго порядка:

d²P ( x ,9

----^—- = -S ( S + 2P ) P ( x , S ) = 0 и гра- dx

x t

;

t x c02     2P

x² безразмерное

время и

x tc0

2P         P

2a t2                t

Введем

координату по t			d	, x d
P	Тогда: P	t	5	P    c 0
t	t	t	"a	t d      ;
2 P	2 P	2 c 0
t 2	t 2	d 2	;
2P	2P	1
2 x	2 x	2	.

Подставляя (12-14)

в

(10,11)

(9), полу-

чим

2P t2

P

+ 2А---= Ц =

2       tx

d a       ). (15)

c ₀

ничное условие P ( x , S ) - — (19, 20)

Общее решение уравнения (18):

P ( x , S ) = c ( S )e S^S⁵⁴^^x+c ₂( S )e S¹⁵¹²^^x

Возмущения, вызванные звуковой волной, во всех точках среды должны быть конечными. Поэтому необходимо положить С] (S) = 0 . Следователь но c2 (S) = —. Решение задачи в изображениях:

P ( x ,S) = 2e"^ ^{S ( S +2Ц}) ^x .

S

Получим решение для звукового давления экрана в оригиналах:

x

P ( x , t ) - 1 e

t

Ie

x

2 x

x

^ T °₀( t-x ) , ⁽²³⁾

_      / _ 9        9

где I     ² x ²

-

функция Бесселя

мнимого аргумента.

Рассмотрим влияния структурного фактора на свойства абсорбента.

Изменения давления в любой точке пористой среды найдем через производную давления по времени:

P        2   -H t I ] (^)                      2     2

xe ¹ (где               x ).

t

При малых значениях аргумента:

11 (^) = E k0

k !Г( k + 2 )   2

2 k 1

где ^r( k + 2) - гамма-функция. Тогда,

P 1   2      x hm Mx-^--^xe           (26)

Из (26) следует, что при <<1 угол наклона касательной к кривой давления - время по зависимости (23) в начальной точке ( t=x ) мал.

При >>1 производная P/ t стремится к нулю в связи с малостью множителя e- x. При 1 эта производная практически обращается в нуль уже при x=3 4. Таким образом, расчеты давления в волне можно производить по формуле:

P ( x , t ) ⁼ e ^ц'^{х a}( t ^—x ) .                  (27)

Если на пакет падает плоская гармоническая волна, то граничное условие для уравнения (27) имеет вид:

P ( x , t ")| x , 0 = P. e-'"            (28)

где P0 - максимальная амплитуда давления в волне, x и t - размерные те- кущие координаты и время.

Тогда, при всех остальных предположениях, решение задачи (26, 27, 28) в безразмерных переменных из решения (23), применяя интеграл Дюамеля:

P ( x , t ) = P o

d

- j® -(^T- x )

_e x _e     c 0            _xe t _e

d

- j® -(^T- x )

c ₀

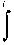
I       ² x ²

² x ²

dt ^( fx ).

Для практического расчета, как это следует из анализа (23), можно пользоваться формулой для оценки спада звукового давления в абсорбенте в зависимости от структурного фактора, с соответствующим его наполнением в виде вязкоупругих потерь для конкретной структу- ры, который и определит диссипативные свойства                    устройства.

d

_     - j® -( t-x )

P ( x , t ) = P _o e"" ^x e    c ⁰     -C( t-x ) .            (30)

В качестве базовых модельных материалов можно использовать полиэтиленовые или полихлорвиниловые трубки, например, сечением 3,5 и 5 мм и длиной 0,25 - 0,3 м, которые могут, на данном этапе исследований, сымитировать структурные параметры абсорбента, сформованного из разнодисперсных компонентов на полимерно-масляном связующем.

Экспериментальная проверка теории сводится к оценки модуля упругости капиллярной модельной системы

Полученные выше решения выполнены в предположении абсолютной жесткости стенок трубок (капилляров) модуля упругости. В основу расчета измерения модуля упругости полимерной трубки принимается формула Н.Е. Жуковского:

^P"^P o----⁽ r"ro ) ,          ⁽³¹⁾

r ₀

где Р-Р0 - избыточное давление в трубке, измеренное манометром; r-r0 -изменение внутреннего диаметра трубки при деформации; h - толщина стенки трубки; Е - модуль упругости полимера.

Формула (31) справедлива для тонких трубок или капилляров h r .

В нашем случае h r, поэтому по- лученное в опытах значение модуля упругости приближенны и характеризуют порядок величин:

• 1 .Начальный объем жидкости внутри трубки: V     r² l ( l - длина

• 2 . Объем жидкости после нагнетания: V      r ² l V      V ;

• 3 .Измерение радиуса трубки:

трубки);

• r - r =    .     (-x V - , У ) "

• r    ^r 0              ⁽ V V V» o ) ;

4.Так как

l

Оценим Из (31):		влияние	погрешностей.
р-р г E   P  P 0 r 0	( P-P o ) Г о				(32)
( r   r 0 ) h		h	.
Тогда      E	<	E --^8 + 6 8	E h	h	или
A E = -( P-P o ) r (	)	11 --+ — h 2	h h	.	(33)

A V«V_Q , □

1 V

V     V 0      V     V 0   1

2 V ₀

то r r

1 V

2 l V

1 V

.

Данные эксперимента сведены в таблицу1.

Характеристики полихлорвиниловой трубки: толщина стенки h=0,1 см; внутренний радиус трубки r 0 = 0,25 см; длина трубки l= 30 см.

2     r 0 l

Табл. 1 - Модуль упругости полихлорвинилового капилляра
номер опыта	V,см3	r-r 0 ,см	p-p 0 , кг/см2	E, кг/см2	номер опыта	V, см3	r-r0, см	p-p 0 , кг/см2	E,кг/см 2
1	0,125	2,7 10-3	1,42	1310	5	0,25	5,4 10-3	2,6	1210
2	“-	-“-	1,38	1280	6	--	66 --	2,55	1200
3	“-	-“-	1,31	1210	7	66 --	66 --	2,55	1200
4	“-	-“-	1,35	1240	8	66 --	66 --	2,52	1190

Из (33) видно, что даже при одинаковом вкладе погрешностей в расчетах r - r 0 = и измерениях диаметра для оценки h, погрешность в оценке модуля упругости не изменит его порядка. Из табл. 1 видно, что модуль упругости испытуемого образца полимерной трубки имеет порядок 10³ кг/см², что на три порядка превышает модуль объемного сжатия воздуха.

В основе расчета параметров звуковой волны, считаем воздух идеальным газом, распространяющейся в податливых капиллярах.

Расчеты на ЭВМ проведены для полимерных капилляров l = 0.3м, радиусом R 0 = 1,5 10^-3м, плотностью = 1,6 кГ/м³ и модулем объемного сжатия Е т = 10³-10⁴ кГ/см². Анализ расчетов показывает, что форма волны (амплитуда равна 1) при ее распространении по упругому капилляру не изменяется с частотой. Таким образом, для данной задачи капилляр можно считать абсолютно жестким. Подобный вывод можно сделать, сверяя результат с решением Н.Е. Жуковского, полученным для избыточного давления с учетом энергетических соображений:

P                 ,           (34)

2 R 0

ETe   EB где l - толщина капилляра, Ет -модуль объемного сжатия материала, EB - модуль объемного сжатия воздуха, -плотность воздуха, - объем воздуха.

Рассмотрим определение спада звукового давления за счет теплопро- водности

На основе закона термодинамики и теории статистической физики Л. Ландау и Е. Лифшиц показали, что коэффициент поглощения звука за счет теплопроводности эквивалентен по чи- словому значению поглощению за счет сил трения. Коэффициент поглощения пропорционален квадрату частоты звука =в 2, в - коэффициент теплопроводно сти. Произведем оценку параметров давления звуковой волны с учетом ее гашения за счет теплопроводности. При поглощении звука:

. Ю .    _2

jв ² .

с ₀

Уравнение бегущей волны, при отсутствии поглощения для давления P(x, t) = (x - ct) можно написать в виде:

P1

5 х

x

Тогда уравнение, решаемое через функцию    e j ⁽ “'t ) ik должно быть:

8 P _   1 5 р Э ² ( р )

в x       c t          t2

x

Введем    t    , тогда уравне- c0

ние (37) получим в виде одномерного уравнения теплопроводности:

P      2P в.

x          t2

Общее решение этого уравнения, в случае затекания в капилляр единичной звуковой волны:

разцом будет при углах =0;   6,   4;

3:

16 h

P ( x , t ) = P_o e ^Цх где ц =--------.    (40)

d ₀ c ₀

Примем в качестве пористого образца прямоугольный параллелепипед с основанием 8 х 8 см и высотой 30 см, собранный в виде сот из полимер-

P ( x ,^T) =

P о (^V) e

в x

_ (V-z)²        _ (t'+t)

4 ‰x        4 ‰x

• d^

Из (39) следует, что амплитуда давления падает обратно пропорционально корню квадратному из расстояния от входного сечения капилляра.

Оценим спад звуковой волны при прохождения сквозь абсорбент. Произведем расчет давления в звуковой волне. Уровни звукового давления регистрируют два приемника, один из которых находится до, а второй за пористым образцом, собранного из пакета полимерных капилляров, которые имитируют глушитель или стенку из абсорбента на машину повышенного теплоизлучения. Структурная постоянная К обратно пропорциональна квадрату конуса угла ( ) между направлением градиента давления и нормалью к поверхности образца. Поэтому, К может принимать значение при , , а вместе с ним и постоянная затухания . Следовательно, P(x,t) . Формула (30) при углах близких к , не применима. Максимальное давления в точка за об-

ных капилляров с внутренним диаметром и толщиной стенок 1 мм. Основными порами в таком образце будем считать полости капилляров. Тогда, при = 64 4         1

0, К =----.-----=------« з. 6 . При л d2"256    0.282

(Р=760    мм рт. ст., t=18 С),

Нс             Нс

182 10 ⁷      ;       123 10 ³      . Т.

мм

16 182 10 7 3,6

о.,

3 10 129 10 340

43 10 ⁴ .

Аналогично вычислим при других углах, имея в виду обратную пропорциональность квадрату косинуса и. обратно пропорционально сos : =  6,    =50 10-4;    =  4,    =61 10-4;

=  3,  =86 10-4

Расчеты относительных давле-

ний P(x,t)/P сведены в табл. 2.

Аналогичные расчеты произведем для пакета из полимерных трубок с диаметром 5 мм и толщиной 1мм.

64 4

2,7 . ( табл. 3).

3,14 0,25 120

=0,  =23 10-4 =  6,  =27 10-4 ,

=  4,  =33 10-4, =  3,  =46 10-4.

Табл. 2 - Расчетные величины относительных давлений для капилляров диаметром 3 мм в зависимости от толщины абсорбента

х		50	100	150	200	250	300
	0	0,81	0,65	0,52	0,42	0,34	0,28
P	/6	0,78	0,61	0,47	0,37	0,29	0,22
P	/4	0,74	0,54	0,40	0,30	0,22	0,16
	/3	0,65	0,42	0,28	0,18	0,12	0,08

Табл. 3- Расчетные величины относительных давлений в капиллярах диаметром 5 мм в абсорбентахразличной толщины

х	50	100	150	200	250	300
fy = 0	0,90	0,79	0,71	0,63	0,56	0,50
P / k=;r/6	0,88	0,76	0,67	0,58	0,51	0,44
P 0 \6 - л /4	0,85	0,72	0,61	0,52	0,44	0,37
^ = л /3	0,79	0,63	0,50	0,40	0,32	0,25

Оценим величину давления на приемнике 2,если на приемник 1 падает волна с давлением 90 дБ, а абсорбент из капилляров диаметром 3 мм. Тогда толщина образца в калибрах равна х = 100.

Примем 6= 3, тогда

90 дБ 20 log

P 1

2 10 ⁵ Па

P      Па

1      10

Такое давле-

ние падает на "тихую" поверхность образца. На выходной поверхности будут значения из табл. 2. Для оценки послед-

него предположим, что волна звукового давления на выходной поверхности получается в виде полусферы, радиус которой равен радиусу круга, площадь ко-

торого равна площади поперечного се-

чения образца, т.е. 8 х 8 см. или

R 0

4.5 см .

Давление в такой

волне будет изменяться пропорционально расстоянию, выраженному в R 0 . При расстоянии от выходной поверхности до приемника 2 равном 60 см –

0 . 84     0 . 065                     P

P ₂       ^{.         .}      Па , P ₂   20 lg             60дБ ,

2    13  10       10         2          2 10 5

л P 30дБ .

Если образец скомпонован из капилляров диаметром 5 мм, то его толщина составляет х = 60 калибров. Расчет показывает, что Р 2 =72 дБ и Р =18 дБ.

В зависимости от диаметра ка-

пилляров, звукоизоляция от чистого эффекта прохождения звуковых волн сквозь пористый образец типа профиля Релея, составляет 30 дБ (3 мм) и - 18 дБ (5 мм) при общей толщине образцов 300

мм,

Таким образом, разработана и исследована аналитическая модель кон-

векционного абсорбента – шумозащитного экрана на базе структуры Релея. Найдено, что полученная структура является по эффективности практически частотно – независимой в слышимом звуковом диапазоне, что облегчает практические расчеты. Исследовано распространение звуковых волны в прямоточных полимерных капиллярах в зависимости от числа Рейнольдса и длины каналов. Найдено решение телеграфного уравнения при соответствующих граничных и начальных условиях. Получена расчетная формула на основе решения интеграла Дюамеля, при выполнении условий Хевисайда для фронта плоских волн, для количественной оценки спада звукового давления в капиллярах, в зависимости от вязкости воздуха и температурных градиентов в пограничных слоях.

Аналитически получено решение для оценки влияния структурного фактора на спад звуковой энергии при прохождении сквозь диссипативный сквозной пористый абсорбент и определены конкретные материалы и расчетные параметры для проектирования экспериментальных абсорбентов.

Разработана методика определения модуля упругости капиллярной структуры для использования в экспериментах и расчетах и проведены аналитические исследования влияния податливости стенок на потери звуковой энергии в структуре, что подтверждено экспериментально и в расчетах на ЭВМ. Аналитически найдено, что конвекционный абсорбент из полимерного материала сечением 30 см, с капиллярами сечением 3 мм, обеспечит эффект снижения уровня шума на 30 дБ, а с капиллярами сечением 5 мм – до 18 дБ, без

учета резонансных эффектов для чисто звукоизолирующих панелей.

В итоге. разработаны аналитические и методические основы проведения экспериментальных исследований по использованию абсорбентов из отходов для средств акустической экологии в целях шумозащиты селитебных территорий от транспортных потоков.