Разработка биоинженерного мехатронного модуля для экзоскелета нижних конечностей человека

позволит медсёстрам и врачам поднимать пациентов с кровати, не прилагая к этому каких-нибудь значимых усилий. Экзоскелет может стать более дешевой альтернативой хирургическому эндопротезированию крупных суставов, которое является довольно сложной и дорогостоящей операцией и не рекомендуемая пациентам с ослабленным здоровьем [2]. Примером подобной реабилитационной системы является японский экзоскелет для нижних конечностей Hybrid Assistive Limb (HAL), представленный на рис. 1.

Рис. 1. Люди с повреждениями опорнодвигательного аппарата со специальным экзоскелетом (HAL)

Современное реабилитационное механоте-рапевтическое устройство (экзоскелет) представляет собой систему со сложной конфигурацией (см. рис. 2), объединяя в себе различные механические и электронные компоненты, призванные в совокупности обеспечивать максимально эффективный и безопасный процесс реабилитации пациентов. При этом большое значение приобретают функциональные возможности каждого узла, из которых и складываются характеристики устройства [3, 4]. Необходимо отметить, что при существующем множестве подобных устройств, предназначенных для людей с болезнями опорно-двигательного аппарата, математическому моделированию их функционирования в составе сложной биоинженерной мехатронной системы уделяется недостаточно внимания.

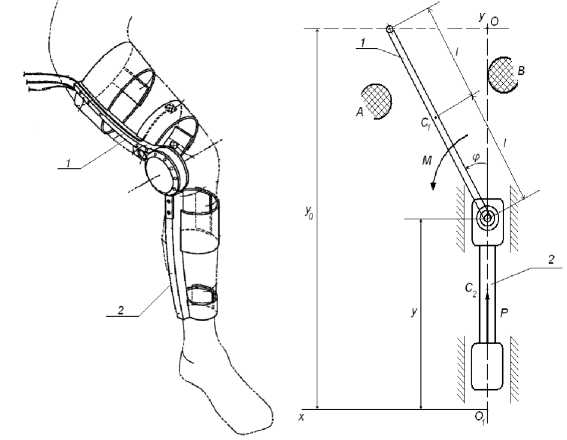
Рис. 2. Экзоскелет для нижних конечностей человека и его расчетная схема

Разрабатываемое биоинженерное реабилитационное устройство для нижних конечностей состоит из двух отдельных модулей с индивидуальными приводами. Со стороны привода коленного модуля к исполнительному звену 1 прикладывается управляющий момент M. Привод поступательного движения модуля мышц голени воздействует на исполнительное звено 2 управляющим усилием Р . С учетом антропометрических данных человека, а также для того, чтобы не нанести вред пациенту, перемещение исполнительного звена 1 коленного модуля дополнительно ограничено препятствиями А и В, поэтому плавное изменение угла поворота ф=ф(1) данного звена возможно лишь в некотором интервале [ ф(0), ф(т) ], где т - время движения исполнительного звена.

Специфика работы механотерапевтического устройства в составе сложной человеко-машинной системы требуют, чтобы исполнительное звено 1 сошло со связи (ограничителя) В в момент времени t=0 и «мягко» коснулось ограничителя А при t=T, т.е. так, чтобы были удовлетворены условия d- ф(t )l t=о, t=т=°;

dt dr Ф( t)11=0, t=t = 0 dt

•

Программное движение звена 1, удовлетворяющее требованиям «мягкого» касания, принимаем в следующем виде:

ф ( t ) = р (0) + [ р ( т ) - ф (0)]

t 1   .Г 2 n t

---sm l--- т   2 п   V т

Центр тяжести звена 1 находится в точке Ci, а звена 2 - С2. Будем считать, что торможение звена 1 начинается в тот момент, когда его угловое ускорение обращается в ноль. Пренебрегая силами сопротивления движению, определим значения управляющих сил и моментов в начале торможения исполнительного звена коленного модуля. Для решения задачи применим уравнения Лагранжа II рода [5]. Будем рассматривать данную биоинженерную систему как механическую систему как систему с двумя степенями свободы, приняв за обобщенные координаты угол φ поворота звена 1 и смещение у звена 2. Для рассматриваемой системы можно записать уравнения связей:

‘ У с 1 = У + 1 cos ф ;

x_c j = l sin ф

4;

В соответствии с выбранными обобщенными координатами имеем dГ 9T )_9T.

dt ^9ф J 9ф d Г 9 T У^^ dt ^9y J 9y

Совокупность уравнений (1) и (2) позволяет составить дифференциальные уравнения движения рассматриваемой механической системы. Составим выражение для кинетической энергии системы Т, как функцию обобщенных скоростей ^ф и ^y и обобщенных координат ф и у . Кинетическая энергия системы равна сумме кинетической энергии Т 1 звена 1 и кинетической энергии Т ₂ звена 2:

m^ ² ml ² ф ²  2 mly ф sin ф J ф ² m₂X ²

T =     +                  +    +

2      2         2        2     2

( m, + m ₇) y ²   ( ml ² + J ) ф ²

= ^{v 1    2}    + ^-1- mlyф sin ф

Найдем значения слагаемых уравнений Лагранжа:

a T   ,,

— = ( m + m ₂) y - mJ ф sin ф;

8y d at   .   .               .-

= ( m₁ + m ₂) y - mJ ф sin ф - mJ ф cos ф ;

dT a y     ^{1    .}........

a t

_ ax’

— = ( mJ ² + J_x ) ф - mjy sin ф ;

Зф d at   ,„

--= ( mJ + J_x )ф - mJу sin ф - mjy ф cos ф ;

dT aф............

a t

— = - mjy t p cos ф .

бф

Определим обобщенные силы Q y и Q φ . Для определения Q y мысленно наложим на систему связь φ=const и, сообщив системе возможную скорость ^y , вычислим возможную мощность сил, действующих на нее: N y = Q y y = ^Py, отсюда

y = 2lф sin ф + 2lф2 cos ф.

Равенства (8) представляют собой зависимость управляющего момента М и управляющего усилия Р от известных функций ^ф , ф и Ф> . Так как φ является заданной функцией времени, то вычисление производных Ф и Ф> , а следовательно, и управляющего момента М и усилия Р не представляет труда. Вычислим М и Р в момент начала торможения звена 1. В этот момент угловое ускорение фФ обращается в нуль. Производные Ф и фФ соответственно равны:

ф = [ ф ( т ) - ф (0)](1 - cos 2 я ? / т )! т _и ф" = 2 П [ ф ( т ) - (0 0)](sin 2 n t / т )/ т ²

Отсюда

2п[ ф(т) - ф(0)]   2п sui t — о, т2

т

т t = —.

Таким образом, торможение звена

2п или —t = П и т

1 начинается в

Q y = ^P

момент

времени t = —. В этот момент

времени

Аналогично, мысленно наложив на механическую систему связь y=const и сообщив ей возможную скорость Ф , получим выражение возможной мощности N : N = Q^ф = Мф , отсюда

Q ф = м

Обобщенные силы Q y и Q φ можно определить и из выражения работы сил на элементарных перемещениях системы, соответствующих вариации каждой обобщенной координаты:

Подставляя (3), (4) и (5) в (2), получим:

Для обеспечения вертикального положения тела человека при ходьбе необходимо обеспечить перемещение крайней точки исполнительного звена 1 вдоль прямой, перпендикулярной оси y , поэтому на механизм дополнительно оказывается наложенной связь y + 2l cos φ = y 0 , или y = y 0 – 2l cos φ y₀=const, следовательно, y = 2l" sin ф . Отсюда

y = 2l ф sin ф + 21ф2 cos ф.

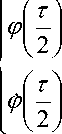
[ ф(0) + ф(т)]

2        ’

2[ ф ( т ) - ф (0)]

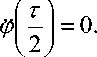
Подставляя (9) в (8), получаем интересующие нас выражения т1

м I   I = - 4 m i l [ ф ( т ) - ф (0)] —sm[ ф (0) + ф ( т )];

V 2 )

т\1

P 12 I = ⁴ l ⁽ m i ^{+ 2} m ^{2 )[} ф ^{( Т} ) - *^{ф (0)]} ? cos

ф ⁽⁰⁾ + ((Ут )

На основе представленных выражений с помощью пакета блочного моделирования Matlab/Simulink получены графики зависимостей управляющих моментов и сил от времени. Вычисления производились в интервале [0;τ] с шагом 0,001τ при следующих исходных данных: m ₁ = 12 кг; m 2 = 6 кг; J 1 = 1,8 кг·м²; l=0,5 м; φ(0)=0; φ(τ)=π/6. Графики зависимостей М и Р от времени показаны на рис. 3, 4.

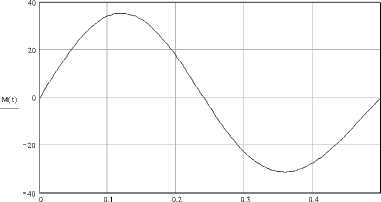
Рис. 3. График зависимости управляющего момента М от времени

Выводы: разрабатываемые биоинженерные мехатронных модули должны учитывать естественные движения в коленном суставе человека и движения совместно с механотерапевтическим устройством. Движение каждого звена влияет на движение остальных звеньев. Указанное взаимовлияние может происходить через механические устройства, общую нагрузку, через общий источник энергии, а также вследствие естественных и искусственных динамических связей между каналами в блоке управления [6]. При этом необходимо формировать управление мехатронной системой (особенно на высоких скоростях, где влияние динамических факторов существенно) с учетом перекрестных связей.

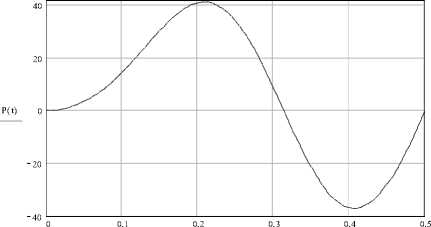
Рис. 4. График зависимости управляющего усилия Р от времени

Для анализа поведения исполнительного звена биоинженерного модуля и проведения численного эксперимента в дальнейшем необходимо разработать уточненную математическую модель проектируемого мехатронного устройства с целью получения необходимых данных, определяющих рабочую область движения исполнительного органа, а также форму траекторий, которую должна обеспечивать система реабилитации для реализации естественных движений нижних конечностей человека, что позволит оптимизировать ее параметры и синтезировать алгоритмы работы и законов управления движением исполнительных звеньев.

Работа выполнена в рамках реализации Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 20092013 годы.