Разработка демодулятора сигнала с неизвестной структурой

Стремительное развитие систем радиосвязи накладывает ограничения на использование частотного диапазона, что делает актуальным проблему контроля и поиска несанкционированных источников радиоизлучения. В статье разработан алгоритм двухэтапного решения задачи, основанный на использовании вейвлет-преобразова-ния [1] и последующей корреляционной обработки сигналов. Предлагаемый алгоритм обработки позволяет определить изменения амплитуды, частоты и фазы входных сигналов с точностью, достаточной для осуществления демодуляции и согласованной фильтрации.

Непрерывное вейвлет-преобразование (ВП) входного сигнала s(t) определяется выражением [1]:

”

W ( a , т ) = J У ( t ) Т I---- \ dt ,           (1)

a -~ I a , где W(a, т) - непрерывное вейвлет-преобразование сигнала; S(t) - входной сигнал; a - масштаб вейвлет функции; t - текущее значение времени; т - сдвиг вейвлет функции по оси времени; T(t) - функция материнского вейвлета; Ta(t) - функции дочерних вейвлеты образованные масштабированием и сдвигом ма- теринского вейвлета; Т* - комплексная сопряженная функция.

Функция Т(0 является материнским вейвлетом, а дочерние вейвлеты Тя(0 получаются масштабированием и сдвигом материнского вейвлета. Простейшим базис- ным вейвлетом является вейвлет Хаара. В отличие от преобразования Фурье, базис ВП локализован как в частотной, так и во временной областях, что позволяет анализировать кратковременные изменения сигналов. Если вейвлет полностью укладывается в тактовый интервал, то модуль ВП Хаара для сигналов с различными модуляции описывается выражениями [1]:

видами

, 4

I HWT kam ( a , т)| = -_r

\ HWT ^ _M ( a , t) = -^— sin² у a ш _н

I HWT _4M ( a , t)| =

,

Ш н Г )

4 I ^,

—=--------sin у a (toH +шi)

,

где s , s - мощность элементарной посылки (ЭП); И _н - несущая частота; to - частота элементарной посылки при частотной модуляции (ЧМ); | HWT _KAM ( a , т ) -модуль ВП Хаара при квадратурной амплитудной модуляции (КАМ); | HWT _OM ( a , т )| - модуль ВП Хаара при фазовой модуляции (ФМ); HWTT^ ( a , т )| - модуль ВП Хаара при частотной модуляции.

ФМ сигнал представляет собой постоянную функцию со всплесками амплитуды, соответствующими тактовым моментам времени, ЧМ и КАМ сигналы представляют собой ступенчатые функции. Известно, что значения дисперсии постоянной функции много меньше дисперсии ступенчатой функции, следовательно, анализируя значение дисперсии входного сигнала, можно выделить сигналы с фазовой модуляцией. Всплески амплитуды входных сигналов устраняются при помощи вейвлет-фильтрации. С целью распознавания сигналов с КАМ и ЧМ необходи мо выполнить амплитудное нормирование анализируемого сигнала в зависимости от соотношения сигнал/шум. Оценка дисперсии вейвлет преобразования амплитудно-нормированного и ненормированного анализируемого сигнала, позволяет определить тип модуляции сигнала.

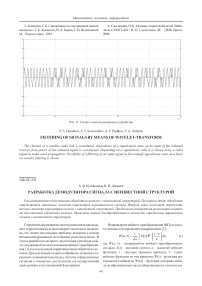
Результат первого этапа обработки сигнала позволяет определить граничные параметры максимальной и минимальной амплитуды сигнала, наибольшей и наименьшей частоты, а также общее количество амплитуд, частот и фаз принимаемого сигнала. Определяемые параметры имеют точную привязку во времени, что позволяет определить информативность сигнала [2]. По полученным данным можно подобрать стандартный демодулятор для демодуляции входного сигнала. Однако для обеспечения наибольшей точности распознавания входного сигнала и для исключения принятия ошибочного решения по выбору демодулятора предлагается использовать корреляционный приемник. Алгоритм формирования данных для многоканального коррелятора приведен на рис. 1.

Входными параметрами являются: количество присутствующих частот А, количество амплитуд А , и количество фазовых скачков во входном сигнале А_ф. В соответствии с этими данными формируются циклы: первый цикл i соответствует числу частот, второй циклу' соответствует числу определяемых фаз, третий цикл к соответствует числу определяемых амплитуд и четвертый цикл т соответствует числу оцифровок, проведенных аналогоцифровым преобразователем (АЦП) за период (рис. 1).

Таким образом, общая картина формирования данных для корреляционного приемника, следующая: для каждого значения частоты, фазы и амплитуды вычисляется т гармоник с длительностью в один период и с разной начальной фазой, т. е. скачок фазы как бы «перемещается» в разные точки периода, что позволяет проводить обработку сигнала без начальной синхронизации. На выходе формируется два вектора:

• 1)5 . - вектор с различными фазовыми скачками;

• 2)    5_i0 - гармонический сигнал с различными частотами и амплитудами.

Разработанный алгоритм двухэтапной обработки сигнала с неизвестной структурой является универсальным, поскольку позволяет системе автоматически подстраиваться под входной сигнал. При этом точность определения параметров входного сигнала ограничена глубиной уровня декомпозиции [1]. Анализ работы алгоритма показал, что корреляционная обработка возможна при уровне шума в два раза превосходящем уровень входного сигнала.

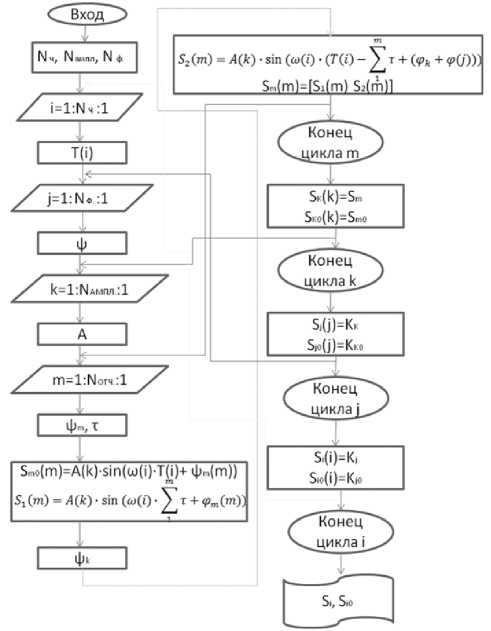
Рис. 1. Алгоритм формирования данных для корреляционного приемника

На втором этапе обработки сигнала амплитуда, частота и фаза определены с предельной точностью, ограниченной шумом. Поскольку каждое изменение ампли- туды, частоты или фазы привязано ко времени, то по результатам обработки сигнала можно построить графики, изображенные на рис. 2.

Анализ графиков (рис. 2) показывает, что в исследуемом сигнале на протяжении всего времени обработки присутствуют 2 различных амплитуды, фазы и частоты. По этим данным можно построить диаграмму рассеяния, которая показывает созвездие исследуемого сигнала. Созвездие сигнала можно построить в трехмерном виде или в виде проекций (Л, у ), (Л, ю ), ( у , ю ). В проекции (Л, у ) созвездие сигнала имеет вид, изображенный на рис. 3.

Анализ созвездия сигнала позволяет определить параметры модуляции входного сигнала, что является основанием для выбора стандартного приемника или синтеза демодулятора учитывающего «тонкую» структуру сигнала. Изложенный подход является уникальным, так как позволяет работать с сигналом, параметры которого заранее неизвестны.

Для реализации разработанного алгоритма обработки сигнала с неизвестной структурой предложена функциональная схема платы (рис. 4). Топология платы имеет гибкую систему настроек, что позволяет не только обнаруживать несанкционированные сигналы в рабочем частотном диапазоне, но и осуществлять их согласованную фильтрацию.

Принцип работы платы (рис. 4) заключается в следующем. Входной сигнал подвергается аналого-цифровому преобразованию, в результате которого образуется серия отсчетов 5k, следующих один за другим с частотой дискретизации аналогово-цифрового преобразователя (АЦП). Полученные отсчеты поступают в блок цифрового сигнального процессора (DSP), где сигнал подвергается быстрому вейвлет-преобразованию. Блок DSP осуществляет двухэтапную обработку, в результате которой накапливается статистика о присутствующих в сигнале скачках амплитуды, частоты или фазы и строится созвездие входного сигнала. Полученная информация поступает в блок программируемой логической интегральной схемы (ПЛИС), где в зависимости от поставленной задачи могут выполняться следующие операции: мониторинг частотных составляющих в необходимой полосе сигнала, сравнение созвездий принятого сигнала с эталонными, сравнение символьных скоростей принимаемого и эталонных сигналов, вычисление энергии сигнала в полосе (по сумме спектральных составляющих), согласованная фильтрация недопустимых информативных параметров (фаз, амплитуд, частот), согласованная фильтрация информативных параметров, следующих с недопустимой символьной скоростью. В блоке постоянно запоминающего устройства (ПЗУ) DSP хранится информация о конфигурации цифрового сигнального процессора, в блоке оперативно запоминающего устройства (ОЗУ) DSP производится запись проме жуточных результатов вычислений. В блоках ОЗУ и ПЗУ ПЛИС также хранятся данные промежуточных результатов вычислений и данные о конфигурации.

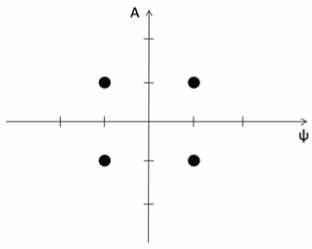
Рис. 3. Созвездие сигнала в проекции (Л, у )

Анализ требований к вычислительным ресурсам для реализации необходимых вычислительных операций показал, что скорость вычисления зависит от полосы исследуемого сигнала. Для анализа использовался сигнал, находящийся в полосе 40 МГц на промежуточной частоте 70 МГц. Для расчетов использовался АЦП фирмы MAXIM (МАХ107) с частотой дискретизации^ = 400 МГц и DSP процессором (TMS320C6701) с быстродействием 5= 10 GFLOPS (миллиардов вычислений с плавающей точкой в секунду).

Число операций, необходимых для вычисления вейв-лет-коэффициентов быстрого вейвлет-преобразования (БВП) вычисляется по формулам [1]:

J , k        j-цП j - 1, n n + 2 k ^,

n

d j , k

E C j - 1,n g n + 2 k ,

n gn = (-1)" h-n+2t+1, где c0 n - вектор входного сигнала; c n - низкочастотный вейвлет коэффициент текущего уровня декомпозиции; d. k - высокочастотный вейвлет коэффициент текущего уровня декомпозиции; ^n + 2k- коэффициенты низкочастотного фильтра для текущего уровня декомпозиции; gn+2k - коэффициенты высокочастотного фильтра для текущего уровня декомпозиции;

Требования, предъявляемые к вейвлет-процессору имеют вид [3]:

S = 2 - ( 2 N + N ) K f = 3 NK A f ,        (6)

где 5 - необходимое число операций в секунду для вычисления быстрого вейвлет-преобразования; А - количество оцифровок на период; К - количество уровней декомпозиции; А/- ширина полосы обрабатываемого сигнала.

Время оценки спектра выберем исходя из анализируемой ширины полосы сигнала [3]:

2 т = —. О_Ц д f

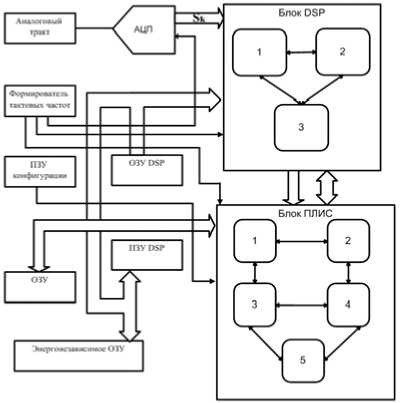
Рис. 4. Топология платы обработки сигналов

Количество оцифровок, которые получаются в результате аналого-цифрового преобразования сигнала за время т _оц равно:

N = f d -т_оц = 2 ■                 (8)

В результате, подставив выражение (8) в (6) получим выражение для вычисления быстродействия DSP:

S = 6 Kf d .                      (9)

Необходимая частота дискретизации определена, исходя из условий теоремы Котельникова [3]. Верхняя частота спектра анализируемых сигналов определяется соотношением:

f . = f „+ f ,               (‘°)

гдеУПЧ - промежуточная частота, на которой осуществляется обработка.

Согласно теореме Котельникова [3], частота дискретизации сигнала определяется из условия:

f , >  ² f , .                      (11)

Исходя из того, что/_ич = 70 МГц, Д = 40 МГц, получим:

f , >  180 МГц.                (12)

Рассчитаем, до какого уровня декомпозиции можно разложить сигнал при использовании DSP процессора с указанным быстродействием за время т _оц:

S      10 - 10 9

K = ---=-------- г ~ 4.

6 f d 6 - 400 - 10 6

На практике для получения наибольшей точности при определении параметров входного сигнала, необходимо обеспечить как можно более глубокий уровень декомпозиции входного сигнала. Рассчитаем необходимое число

DSP процессоров с быстродействием 10 GFLOPS, чтобы разложить сигнал до сотого уровня декомпозиции вейв-лет-коэффициентов (с учетом того, что современные процессоры выполняют за один такт 6 операций) [4]:

100 m =    = 4.

4 - 6

Проведенный анализ быстродействия для вычисления быстрого вейвлет-преобразования в реальном масштабе времени показал, что для реализации алгоритмов первого этапа обработки необходимо использовать одновременно 4 DSP процессора типа TMS320C6701. Несмотря на технические сложности при реализации данного алгоритма, выигрыш в точности при определении параметров сигнала с неизвестной структурой позволяет создавать на базе предложенной топологии платы различные системы контроля частотного диапазона и фильтрации несанкционированных сигналов. Кроме того, на базе предложенного алгоритма обработки сигнала можно создать согласованный демодулятор с гибкой архитектурой топологии платы.

Таким образом, предложенный в статье алгоритм обработки сигнала с неизвестной структурой является перспективным, поскольку позволяет решать широкий круг задач, связанный с определением параметров, фильтрацией и демодуляцией сигнала с неизвестной структурой.