Разработка гибридного алгоритма обучения структуры динамической байесовской сети на основе метода Левенберга - Марквардта
Автор: Азарнова Татьяна Васильевна, Баркалов Сергей Алексеевич, Полухин Павел Валерьевич
Рубрика: Информатика и вычислительная техника
Статья в выпуске: 4 т.18, 2018 года.
Бесплатный доступ
Для моделирования сложных стохастических процессов функционирования современных многопользовательских информационно-коммуникационных систем достаточно эффективно применяются динамические байесовские сети. Динамические байесовские сети представляют собой графические вероятностные модели, отражающие топологию и стохастические причинно-следственные связи между элементами моделируемых процессов обработки информации. Построение топологии динамических байесовских сетей, адекватно отражающей вероятностные и функциональные связи между элементами процессов, является ключевым фактором успеха при моделировании с помощью данного инструментального средства. Топология сетей, как правило, строится или экспертным путем, или на основании обучения. Механизмы обучения позволяют получить остовную структуру сети, а также определить условные связи и их направленность между отдельными вершинами сети. В статье рассмотрены вопросы применения математического аппарата проверки статистических гипотез о наличии зависимости между случайными величинами, опирающегося на статистические критерии Пирсона, Шварца, Акаике и Байеса - Дирихле. В отличие от статических байесовских сетей при определении структуры динамических байесовских сетей необходимо определять переменные и связи между ними не только внутри одного среза, но и между переменными различных срезов, которые реализуют транзитивные связи между временными этапами функционирования некоторого процесса или объекта. Построение структуры транзитивных связей между срезами является достаточно сложным и проблемным этапом почти всех существующих алгоритмов. В данной статье в рамках оптимизации алгоритмов построения динамических байесовских сетей с транзитивными связями между срезами представлен алгоритм обучения структуры динамической байесовской сети, базирующийся на методе Левенберга - Марквардта.
Динамические байесовские сети, обучение структуры, статистические критерии проверки независимости между случайными величинами, метод левенберга - марквардта
Короткий адрес: https://sciup.org/147232214
IDR: 147232214 | УДК: 519.86 | DOI: 10.14529/ctcr180402
Development of the hybrid algorithm of tutoring of structure of dynamic Bayesian networkon the basis of the Levenberg-Markvardt method
Dynamic Bayesian networks are used quite effectively for modeling complex stochastic processes of modern multi-user information and communication systems. Dynamic Bayesian networks are graphical probabilistic models that reflect topology and stochastic cause and effect relationships between elements of the handled simulated information processes. The construction of topologies of dynamic Bayesian networks that appropriately reflect the probabilistic and functional relationships between the elements of such processes is a main factor in the simulation using this tool. Network topology usually built either by expert means or be means of training. Training mechanisms allow to get spanning tree of the network, as well as to determine the conditional connections and their direction between the individual vertices of the network. In this article regard the usage of mathematical apparatus for testing statistical hypotheses based on conditional independency tests between random variables with the Pearson criteria, Schwartz, Akaike and Bayes-Dirichlet metrics. Unlike static Bayesian networks, when determining the structure of dynamic Bayesian networks, it is necessary to determine variables and relations between them not only within one slice, but also between variables of different slices, which implement transitive connections between the time slices that reflect functioning of a certain process or object. The construction of structure of transitive links between slices is a rather complex and problematic step in almost all existing algorithms. This article presents an algorithm for learning the structure of a dynamic Bayesian network based on the Levenberg-Marquardt method within the optimization of algorithms for constructing dynamic Bayesian networks with transitive links between slices.
Текст научной статьи Разработка гибридного алгоритма обучения структуры динамической байесовской сети на основе метода Левенберга - Марквардта
Процедура обучения динамических байесовских сетей представляет собой сложный и многоаспектный процесс, требующий детального понимания вероятностных и временных связей между узлами сетей. Одним из ключевых факторов обучения является наличие априорной информации, полученной с помощью различных эвристических средств в процессе ретроспективного или текущего анализа прикладной области. Построение сети, как правило, сводится к построению некоторой базовой топологии, и настройки вероятностных связей между вершинами сети с помощью проверки статистических гипотез. Применение различных статистических критериев позволяет определить, какая из вершин является родительской или дочерней по отношению к другой вершине. Анализ существующих алгоритмов обучения структуры байесовских сетей показывает, что нет единого универсального алгоритма, который при моделировании процессов из различных предметных областей, имеющих различную специфику вероятностного распределения взаимосвязанных элементов процессов, обладал бы более высокой эффективностью по сравнению с другими алгоритмами. Все основные алгоритмы имеют свои достоинства и недостатки в решении задач определения топологических связей между узлами сети и направленности данных связей. Апробация различных алгоритмов показывает, что более качественное описание сложных процессов удается получить с помощью гибридных алгоритмов обучения, позволяющих комбинировать несколько различных математических подходов в единый алгоритм. Проблемными зонами большинства алгоритмов обучения структуры динамических байесовских сетей является определение вершин, которые реализуют транзитивные связи между временными срезами и определение направленности данных связей. Наличие временных связей между вершинами соседних временных срезов свойственно не только вершинам, занимающим одинаковые позиции в структуре среза, но и вершинам с различной функциональностью в структуре среза. В статье рассмотрены вопросы, связанные с повышением эффективности решения описанных проблемных точек алгоритмов, и предложен оригинальный гибридный алгоритм обучения структуры динамической байесовской сети.
Критерий условной независимости при определении семантики динамических байесовских сетей
Байесовские сети представляют собой разновидность графических вероятностных моделей. Статическая байесовская сеть строится как ациклический ориентированный граф, состоящий из множества вершин Х — {Х1,Х2, .^,ХП}, соединенных дугами. Направление дуги от вершины Х 1 к вершине Х2 говорит о том, что переменная Х1 является родительской по отношению к переменной Х2. Вершины байесовской сети рассматриваются как случайные величины, в соответствие каждой из них ставится некоторое распределение вероятностей Р(Х), при этом если вершина имеет одну и более родительских вершин, то такое распределение будет условным Р(Х|рагеп(5(Х)) [1]. Понятие динамической байесовской сети является некоторым расширением понятия статической байесовской сети, динамическая байесовская сеть может быть представлена в виде нескольких байесовских сетей, взятых в определенной хронологической последовательности. Время может рассматриваться как дискретная или непрерывная характеристика анализируемых процессов; в рамках данного исследования предполагается, что время носит дискретный характер, и для системы связей между временными срезами выполняется свойство Марковских цепей.
Обучение динамических байесовских сетей функционально разделяется на обучение структуры графа и параметров вершин. Обучение параметров направлено на получение начального распределения вероятностей Р(Х0) для всех вершин первого временного среза сети. В данной статье основное внимание уделяется процедуре обучения структуры сети. Процедура обучения структуры производится на основе статистического анализа обучающей выборки, содержащей множества значений, принимаемых вершинами (узлами) сети [2]. Хорошие результаты обучения в процессе апробации показывают гибридные алгоритмы на основе ограничений условной независимости и оценки качества. Остановимся на математическом аппарате алгоритмов на основе выполнения гипотезы условной независимости. Сущность понятия условной независимости в терминах байесовских сетей тесно связана с понятием Марковского покрытия [3]. Для проверки гипотез об условной независимости вершин байесовской сети используется критерий / 2 Пирсона. Основная сущность данного критерия заключается в оценке принадлежности выборки Х вероятностному распределению Р(Х). Если выборка Х = (Х1,Х2,..,ХП) принадлежит распределению Р(%), то каждый интервал значений элементов выборки Х ; может быть разбит на m интервалов / = (/1, /2, ..., /т) и вероятность попадания в данные интервалы будет определяться на основе следующего выражения [4]
Р(Х;) = ];р(Х)^Х = Е/Р(Х).(1)
В рассмотрение вводится следующая статистика критерия:
2гу —V ^ N a,b,c ~ E a,b,c ) _ Ф(Ь |с)—,Р(Ь | а,с))
Z (Х,Y |Z) — !аДс _ Пас , где Na,b,c - частота появления значений Х — a,Y — b,Z — с, Ea,b,c - ожидаемое число вхождений значений Х — a, Y — b, Z — с, которое определяется следующим образом:
Eabc — ^^С
U^C^
Гипотеза об условной независимости отвергается, если величина / 2 принимает неправдоподобно большие значения.
В рамках разработанного в данном исследовании гибридного алгоритма критерий Пирсона используется как мера оценки устойчивости связи Л(Х, Y|Z) между переменными Х, Y. В резуль-
Информатика и вычислительная техника
тате проведения тестов на условную независимость формируются множества родительских и дочерних вершин, связанных с каждой вершиной байесовской сети. На основании этих множеств формируется ненаправленная структура байесовской сети. Для определения направленности связей между узлами байесовской сети необходимо произвести поиск направленного графа с максимальным значением выбранной индикативной оценки. Изменение оценки напрямую связано с операциями добавления, удаления и изменения направленности связей между узлами байесовской сети. В качестве подобных оценок используются различные критерии: логарифм правдоподобия, критерий Шварца, Акаике и Байеса-Дирихле [5].
Значение логарифма правдоподобия для оценки направленности байесовской сети определя- ется выражением
L(G,6e,D) = L?-i2’-i2?-iNt,,,eln^^.(4)
l'j
Критерий Шварца и Акаике строятся на основе вычисления логарифма правдоподобия (4).
Обобщенное представление данных критериев имеет следующий вид:
Q(M) = L(G,6C,D)-MF(N),(5)
где N - размер обучающей выборки, M - число параметров байесовской сети Q G :
M = S[-i(rt-1) qt.(6)
Используя выражения (4) и (6), обобщенное представление критериев Шварца и Акаике (5)
можно записать в следующем виде:
Q(M) = E F-i S j-i S fc-i N tj, kln ^^ -Z [Li (ri - 1) q t F(N).
Множитель F(N) является вариативным и может принимать значения F(N) = 1, если рассматривается критерий Акаике и F(N) = ^ для критерия Шварца. Критерий Байеса - Дирихле определяется через распределение Дирихле, а значения условных вероятностей вычисляются на основе локальной и глобальной независимости вершин байесовской сети. Выражения для критерия Байеса – Дирихле имеет следующий вид [6]:
рГп\ГА— Пn n9 i Г (^ k=i a i'j's ) nr i Г^ Nlj's+aM's )
P(D|G) = nt=in'-ir(z:L1«u,+«u,)n”1 г^,) - где D = {Di = {Xf = 1,Х§ = 2Х^ = n},D2 = {Xf = 2Х = 3Х^ = и - 1}Dm = = {Х^ = 3,Х£ = 1, ,„,Хщ = 2}} - совокупность обучающих выборок для 6е, входящих в состав байесовской сети.
Разработка гибридного алгоритма обучения на основе метода Левенберга – Марквардта
Применение классических гибридных алгоритмов для обучения структуры динамической байесовской сети становится достаточно сложным, из-за присутствия связей между временными срезами сети. Для обхода данных ограничений в статье разработан и апробирован гибридный алгоритм обучения динамической байесовской сети на основе применения инструментов цепей Маркова и метода Левенберга – Марквардта. Алгоритм структурно разделяется на два основных шага решения задач обучения сети.
На первом шаге происходит определение базовой структуры динамической байесовской сети за счет формирования Марковского покрытия для каждого из узлов. Основой для построения Марковского покрытия является обработка тестов на условную независимость в соответствии с критерием Пирсона (2). Для работы с узлами сети, имеющими временные связи, используется математический аппарат цепей Маркова. При этом предполагается, что Марковская цепь является однородной. В процессе выполнения алгоритма происходит определение узлов-кандидатов, которые могут быть добавлены в Марковское покрытие M для переменной Z. Для удаления ошибочно добавленных вершин предполагается повторное выполнения статистических тестов для каждого подмножества MEM. Если переменная Z является временным узлом сети, то Zt и Zt+i описывают состояния данной переменной в моменты времени t и t + 1. Марковское покрытия для динамической байесовской сети до момента t + 1 включительно можно представить в виде следующего выражения
Mt:t +i = Mt U M t+i . (9)
С учетом предположения о Марковости рассматриваемого перехода, Марковское покрытие Mt+1 будет соответствовать множеству дочерних вершин С t+1, имеющих непосредственную связь с переменными из состояния t [7]. Процедура поиска ненаправленной структуры динамической байесовской сети состоит из следующих этапов.
На начальном этапе происходит определение входных параметров алгоритма: обучающая выборка D, текущая переменная Z и Марковское покрытие M t.t+1 = 0.
На следующем этапе в цикле производится анализ устойчивости связи между текущей переменной цикла Х , и переменной Z при наличии всех подмножеств M* с M t.t+1 на основе вычисления критерия Пирсона. Если значения критерия превышает некоторое критическое значение с уровнем значимости 1 — а, то гипотеза об условной независимости отвергается, а переменная добавляется в состав Марковского покрытия.
В результате выполнения первого этапа алгоритма формируется результирующее Марковское покрытие, соответствующее искомой ненаправленной структуре динамической байесовской сети.
Для определения направленности связей между узлами динамической байесовской сети используется алгоритм локального поиска на основе метода Левенберга – Марквардта. Метод обладает достаточной высокой эффективностью и сводит к минимуму вероятность попадания оценочной функции в локальный оптимум. В общем случае метода Левенберга – Марквардта представляет комбинацию градиентного метода и метода Гаусса – Ньютона [8]. В основе метода Гаусса – Ньютона лежит метод наименьших квадратов, позволяющий произвести минимизацию искомой оценочной функции ^(w) (критерии (4), (7) и (8)):
V(w) = min||0(w)||2 = ^k=i(.9k(w) — ak)2,
где [gk(w) — a k ] k^1 — разностное выражение для градиента g k (w).
Для работы с функцией (10) вводится матрица Якоби:
/(w) =
|
г dg i (w) |
dS i (w)-i |
|
dw t |
dwn |
|
dg2(w) |
dg 2 (w) |
|
dwt ' |
' dwn |
|
■■■ dgm(w) |
■ dgm(w) |
|
- dwt |
dwn - |
,w е Rm
Транспонированная матрица по отношению к Якобиану (11) является градиентом F (w):
F' (w) е R -'F F'(w) ,, = ^(w),F'(w) = J(w) = ^F(w)T . (12)
Используя Якобиан (11), можно определить значение w ,+1 , если дано начальное значение w , :
w !+i = w
—
T ^ (w / )f(w 2 )
JT(W j) J(W j)"
Для формулировки метода Гаусса – Ньютона необходимо определить следующее неравенство
UT(w)J(w)] > Q(w)
С учетом того, что неравенство (14) допустимо только в тех случаях, когда Q(w) ^ 0, выражение для метода Гаусса - Ньютона в точке w,+1 имеет следующий вид w,+1 = w, — [JT(w)J(w)]-1JT(w)F(w). (15)
Основным недостатком метода Гаусса – Ньютона является плохая сходимость в тех случаях, когда значения Q(w) ^ да .
В основе метода Левенберга – Марквардта в качестве критерия оптимизации используются модели данных на основе обучающей выборки, а сущность авторского подхода заключается в поэтапной аппроксимации определенных начальных значений параметров к локальному оптимуму. Основой для построения метода Левенберга – Марквардта является регрессионная выборка D = {(x k ,y k )'} k=1 , У = f (х) [9]. Сама же регрессионная модель задается в виде непрерывной и дифференцируемой функции f(X k , w). Второй параметр функции w определяет степень близости ожидаемых значений y k и действительных значений y k . В таком случае задача обучения на основе критериев (4), (7) и (8) может быть сведена к минимизации следующей функции
Информатика и вычислительная техника
E(w) = Sfc=i№k,w) -Ук)2,
w' = argminweflm E(w).
Исходя из выражения (16), значение градиента и Гессиана, соответствующие функции E(w), принимают следующий вид
-dE_2^i№k,w)-yk)
dw ^
d/(X fc ,w) dwi ’
d 2 E _ /d/(X fc ,w)\T df(X k ,w) dw ^ w j V dwi / dw j
■У к . . , w v . ' - ,.•
С учетом того, что первое слагаемое представляет собой произведения матриц Якоби, обобщенное выражение для Гессиана можно переписать в следующем виде
H _/T(w)/(w) + R(w), (18) где R(w) - второе слагаемое выражения (18), описывающее вторые производные для функции f(x k ,w).
С учетом того, что матрица /T(w)/(w) является положительно переделённой, Левенбергом был введен параметр регуляризации Л > 0. Формула решения уравнения относительно Aw имеет следующий вид [10]
Aw _ (/ T (w)/(w) + Л/(w)) 1/T (w), (19) где /(w) - единичная матрица.
Корректировка параметра регуляризации Л происходит на каждом шаге метода. Искомым значением Aw является значение, полученное на последней итерации. В свою очередь, классический метод Левенберга был преобразован Марквардтом, так как при увеличении Л, скорость аппроксимации R(w) существенно снижается. Для этого единичная матрица /(w) может быть заменена на диагональ Гессиана:
Aw _ UT(w)J(w) + Лdiag(Jт(w)J(w)))”1Jт(w'), (20)
Выражение (20) описывает классический метод Левенберга – Марквардта. Исходя из того, что у метода Левенберга - Марквардта Гессиан пропорционален кривизне функция /(w), то данное выражение будет приводить к малым итерациям при большой кривизне и большим при малой кривизне. Рассматривая данный метод применительно к процедуре обучения, видно, что вероятность попадания значений в локальные оптимумы достаточно мала, по сравнению с другими методами благодаря использованию параметра регуляризации Л. Это позволяет корректировать поведение метода в процессе проведения обучения. На начальных этапах выполнения метода, когда значения функции /(w) не являются точными, используется метод Коши (Л >> 0). В дальнейшем по мере означивания параметров w целесообразно брать значения Л _ 0 и использовать метод Ньютона – Гаусса.
Проанализировав метод Левенберга – Марквардта, можно сказать, что его применение в процедуре обучения структуры динамической байесовской сети является обоснованным. В связи с этим разработанный гибридный алгоритм обучения структуры байесовской сети на основе объединения процедуры выполнения статистических тестов и метода Левенберга – Марквардта может быть разделен на два основных этапа.
На первом этапе происходит заполнение множеств Mt:t+1 на основе узлов-кандидатов в состав Марковского покрытия и исключения ошибочно добавленных переменных за счет выполнения / 2 тестов. Тем самым происходит определение базовой (ненаправленной) структуры байесовской сети.
На втором этапе происходит определение направленности связей за счет вычисления оценок на основе метода Левенберга – Марквардта. Данный процесс характеризуется операциями добавления, удаления и изменения направленности связей, которые, в свою очередь, приводят к изменению оценок, назначаемых каждому из узлов сети.
Далее приведем зависимость критериев Шварца, Байеса – Дирихле, логарифма правдоподобия Акаике от размера обучающей выборки. Также оценим погрешность каждого из критериев методом Левенберга – Марквардта относительно критерия Байеса – Дирихле (см. рисунок).
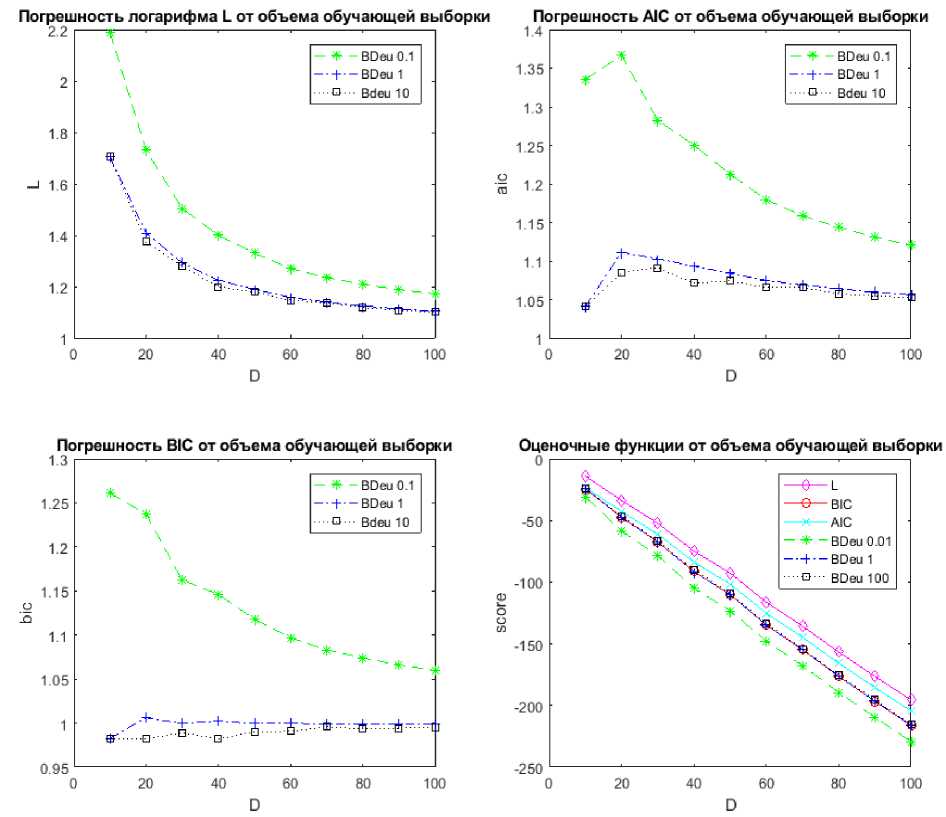
Зависимость значений оценочных функций от объема обучающей выборки методом Левенберга – Марквардта
Для п ров ед е н и я э кс п е риме н та по построению структуры байесовской сети б ы ли в зяты се ти : Alarm ( 37 у з л ов, 46 дуг , 509 п а раметров), Water (32 узла, 66 дуг, 10 082 параметра) и Mildew (34 узла, 46 дуг, 540 150 п ара ме тров). Таким образом, применение предложе н ного а л гори тм а по зв оли т оп ти ми зи ров а ть проц е д у р у построения структуры динамической байес ов с к ой сети, а так ж е а д а п ти рова ть алгори т м к а н а л изу временных связей между вершинами на ос н ов е ма те м а ти че ск ого ап парата М а рк ов ск и х ц е п е й .
Заключение
М а те ма ти чес к и е а лг ори т мы обучения структуры динамических байесовс ки х с е те й яв ляю тс я важным аспектом построения сложных разветвленных сетей обработки инфо рма ц и и в с ов ре ме нных информационно-к ом му н и к ационных системах. От реализации данных алгори тмов н а п ряму ю за в и с и т э фф е к ти в н ос ть при ме н е ния процедур прогнозирования параметров се ти м е тод а ми в е роятностного вывода. Примен е н и е процедур обучения параметров и структ у ры с е ти п озв оляет ад а п ти ров а ть и п ровес ти н а с тро йку сети на решения различного рода задач. В с в язи с э ти м раз р а б отка н ов ых алгори тмо в обуч ения структуры динамической байесовской се ти яв ляе тс я од н им из приоритетн ы х н а п ра в л е н и й развития инструментов моделирования с помо щ ью д и на ми че ск и х ба й е с ов ск и х с е те й . В рамк а х исследования, описанного в данной статье, раз ра б от ан ори ги н ал ь н ы й а лго ри тм об у че н ия ст ру к ту ры н а основ е мет о д а Ле в е н б ерга – Марквардта. Апробация применения да н н ого алгори т ма да ла достаточно хорошие результаты. Алгоритм п озв оляе т с озд а т ь ад а п ти в н ую с а мооб у ча ющ у ю с я динамическую байесовскую сеть на основе пос трое н и я п рям ы х и
Информатика и вычислительная техника
перекрестных связей между разнесенными во времени статическими байесовскими сетями. В статье представлена оценка качественных и количественных показателей алгоритма в процессе построения ряда динамических байесовских сетей из различных предметных областей. Эмпирические данные, полученные с использованием представленного алгоритма, доказывают эффективность выбранного математического аппарата и корректность выполнения основных процедур обучения структуры динамической байесовской сети.
Список литературы Разработка гибридного алгоритма обучения структуры динамической байесовской сети на основе метода Левенберга - Марквардта
- Darwiche, A. Modelling and Reasoning with Bayesian Networks/A. Darwiche. -New York: Cambridge University Press, 2009. -548 p.
- Friendman, N. Learning the structure of dynamic probabilistic networks/N. Friedman, K. Murphy, S. Russel//Proceedings of the Fourteenth conference of Uncertainty in artificial intelligence. -SanFrancisco: Morgan Kaufman, 1998. -P. 139-147.
- Тулупьев, А. Байесовские сети, логико-вероятностный подход/А. Тулупьев, С. Николенко, А. Сироткин. -СПб.: Наука, 2006. -728 с.
- Кельберт, М.Я. Вероятность и статистика в примерах и задачах. Т. 1: Основные понятия теории вероятности и математической статистики/М.Я. Кельберт, Ю.М. Сухов. -М.: МЦНМО, 2007. -456 с.
- Schwarz, G. Estimation dimention of a Model/G. Schwarz//The Annals of Statistics. -1978. -Vol. 6, no. 2 -P. 461-464.
- Рассел, С. Искуственный интеллект: современный подход/С. Рассел, Р. Норвиг. -М.: Вильямс, 2006. -1408 с.
- Азарнова, Т.В. Разработка динамических байесовских моделей управления процессами тестирования веб-приложений/Т.В. Азарнова, П.В. Полухин//Актуальные проблемы прикладной математики, информатики и механики: материалы Междунар. науч. конф. -Воронеж: Научно-исследовательские публикации, 2017. -С. 490-498.
- Стрижов, В.В. Методы индуктивного порождения регрессионных моделей/В.В. Стрижов. -М.: Вычислительный центр им. А.А. Дородницына РАН, 2008. -62 с.
- Вержбицкий, В.М. Численные методы. Линейная алгебра и нелинейные уравнения/В.М. Вержбицкий. -М.: Издат. дом «Оникс 21 век», 2005. -432 с.
- Васин, В.В. Метод Левенберга -Марквардта и его модифицированные варианты для решения нелинейных уравнений с приложением к обратной задаче гравиметрии/В.В. Васин, Г.Я. Пересторонина//Труды института математики и механики УрО РАН. -2011. -Т. 17, № 2. -С. 53-61.


