Разработка и анализ системных параметров исходного процесса в узле систем автоматизированного проектирования технико-экономических процессов по функции времени

^r i ^l(t) =

b i ( t)exp( —A t) при i> 0;

A exp( —A t)    при i= 0.

Из этого следует ril(S) = 5^ b,(S).      (7)

A + S где b0(S) = 1.

В соответствии с зависимостями теории восстановления рассмотренная последовательность случайных величин Tk (k > 1) образует процесс восстановления с запаздыванием, при этом, если hi(t) – плотность вероятности восстановления, i – первоначальное число требований в системе, то имеем в соответствии (7) равенство вида hi (S) = Ab( S )/[A + S - ЛЬ (S)]. (8)

Определим следующие вероятности

P(m, X t)d / = P[m(t) = m /< z < / + d / l mo) = i], 1 <  m <  N;

1 i (t) = P[m(t) = 0lm(o) = i] .

Производящая функция системы имеет вид

Положив m = 0 и используя (11) и (12), получим N A lA(0) = 1 - l.

При m = 1 с учетом (15) получим

" N K N - 1 1

E(m) = N(1 - 1) - N A A-i) = N1 - 1 У    —

_ l = 0 V l J Pyl)

. (17)

В соответствии с выражением (13) уравнение (17) запишем в виде (математическое ожидание числа запросов в узле)

N - 1

E(m) = N(1 - 1) - N A A(1) = N 1 - 1 У

l = 0

( ^{N - 1} 1

V 1 J P(1)

. (18)

I( A S) = У О* J P(m, % ,S)d %= l i (S()[1 + NAn₁(a,S) + I( a S)], m = 1 0

где П 1(a,S) = П( a ,S) ; П 0 ( a , S ) = 0 ;

₁ =       b i (S)

i N A + S - N A b(S)^,

что следует из (8); кроме того, bi (S) определяется из соотношения (5), причем bi(S) = b(S); bo(S) = 1.

Обращение этих выражений во временную область – задача весьма сложная. Учитывая то, что необходимо исследовать поведение процесса в окрестностях только точки с нагрузкой, равной единице, имеет смысл оценить предельное поведение полученных зависимостей, полагая V = ~ :

P(m) = N VJ P(m, _Z )d % = N A У - 1) 0                     l = 0

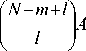
(N - m + l) (11)

где

A(m ) =

F(m - 1)^N у ¹ m A      l = m

( N - 1 ) 1

V l J Wp ⁽¹²⁾

n - 1 <  N

A(0) = V У

l = 0 V l

N -1( N l = 1 + NAv У

J

-

F(l);

h i (S) =

l = о V l J F(l)’ A b i (S)

i

A + S - A b(S)

.

F ( l ) задается соотношением (2).

Используя выражение (9), получим выражение для среднего числа запросов. В силу (13) и (12) соотношение (11) перепишем в виде

Таким же способом можно получить и остальные моменты.

Обозначим через Q * величину N Av и рассмотрим изменение E(m ) и (1 - l ) (занятость системы) в предположении, что время обработки имеет экспоненциальное и постоянное распределение.

Из выражения (18) следует, что влияние функции распределения времени обработки весьма существенно в точке Q * = 1 , а при Q * >  1 влияние вида функции распределения весьма мало.

При Q * >>  1 величина l —> 0 и N —> ^ , так что

E(m) ^ N(1 - 1/ Q *) . (19)

Таким образом, какое бы распределение времени обработки не имело место, график функции E ( m ) асимптотически приближается к прямой, проходящей через точку (1,1 - 1 / Q *) под углом arctg (1 - 1 / Q *) , то есть E(m ) с большой точностью можно аппроксимировать прямой. Точное исследование подтверждает результаты исследований.

Кроме длины очереди в окрестности Q * ~ 1 необходимо определить время ожидания обработки. Поэтому расчет времени ожидания обработки управляющих программ в САПРТЭП проведем, основываясь на вышеизложенных предположениях. Обозначим через W i ( t ) время, необходимое для полной обработки всех запросов, которые присоединились к очереди до момента t исходного процесса (время разгрузки). Плотность распределения W i ( t) обозначим через to^T ,t) . Для дисциплины очереди – «пришел первым – первым обслужен» – интервал [3] разгрузки равен времени ожидания запроса при условии его поступления в момент времени t .

Найдем выражение to i ( T ,t) через W i (t) , равное интервалу разгрузки процессора в момент времени t на периоде занятости.

Учитывая, что

N - 1( N          N - m^ N _- tX

N A lA(m) = У I I P(N - 1) = У I I P(l). (16) l = m V ^m J l = 1 V ^m J

to i ( T ,t)d T = P[ t <  W i (t) < t + dtlm(0) = i] ,(20)

имеем

_m_ i ( 9 ,S) - J J e ^- St . e -^0r_Mi (t, т )dtd T - 00

- J E P-M Z SHB P )]^md z J B J ^{X +} y) . e

B ^{( 6})^{0m - 1}                        0 1 - J B(u)du

Используя выражение (20), получим to(9S)-^№1 j[1 -B(9)]a-i(j,S)B(j;t+ S)-B(9) B(9) j -o                          9- jA-S где a-6( j, S) определяется из выражения (6).

Учитывая, что при и < j limtoi(T,t) - т(т) не зависит от начальных условий, получим toP-°J«(T)eтт-1\1 -NAjBe]' .[1 -B(9)JA(j)-j-B9 Bj) 1,(2 1) o [    j=o                      1 -BjA) jA-e где А(j) и l задается формулами (11)-(15).

Средняя длительность интервала разгрузки равна

E ( to ) -

N A и

N Au + e

' _n 1 - e 1 E ( B 2 ) ( N - 1) u ^ ■

A 2 и

, (22)

мации в узле, нагрузка на который p <  1 и только в отдельные моменты времени может приобретать значение p >  1 с последующим обязательным возвращением к значениям p <  1 .

Учитывая, что в комплексе технических средств таких узлов достаточно много, особый интерес представляет случай, когда в критических ситуациях ( p > 1) находятся несколько или все узлы системы. Не снижая общности рассуждений, выделим на любом маршруте m таких узлов с номерами m 1 , m₂,^, m n ( n в общем случае ^ j ). Рассмотрим совместное поведение этих узлов.

Введем в рассмотрение следующую последовательность временных интервалов t [бесконечную матрицу]:

т l      T^S

^T ji ’—, ^T j1

lS

^T j2 ,..., ^T j2

где — - e

N - 1

X l - 0

^ N -

< l

1 ) 1

) F(l)

Перепишем равенство (22) в виде

E( to )/ u - N - f(1 - l)/ u ,  (23)

где f - и + 1/A - E(B² )/2 u .

Представляет интерес анализ результата (23) при p* » 1 и больше N .

Применяя те же соотношения, что и в случае анализа функции E(m) , получаем

^T jn ’...^{, T} jn

где T j_n - интервалы времени между поступающими запросами;

T S - интервалы времени обработки;

n – номер узла;

j – номер цикла взаимодействия и номер элемента в этой последовательности.

Обозначим также через M Р ( т ) момент порядка b от случайной величины t .

Введем следующее предположение для функции распределения:

E( to )/ u - N(1 -1/ p *) -1 + E(B²)/2 U , (24) то есть график e ( to ) / U асимптотически стремится к прямой, вид которой зависит от второго момента функции распределения времени обработки E( B ² ) .

Тогда при больших p * значение E( to )/ U можно вычислить по формуле (24).

Полученные зависимости показывают, что при работе любого узла в режиме большой нагрузки его параметры связаны линейными зависимостями. Этот результат позволяет резко упростить вычисления при синтезе управляющего вычислительного комплекса САПРТЭП, а также получить зависимости, позволяющие определить в явном виде параметры процессов в различных узлах маршрутов передачи информации в предположении, что известны точные характеристики, как процесса появления запросов, так и параметров обработки, причем на эти характеристики накладывались определенные ограничения.

Однако эти зависимости были получены для случая выполнения обработки и передачи инфор- p(TSn > х) - exp(^np));

M T SSn - 1 / a n;

M ^T in   ,

--- d a„ ^ 0   при m ^ J

M T S   n n

где a n и d_n - некоторые произвольные постоянные. Рассмотрим установившийся процесс, поэтому вместо условия n —> j будем писать эквивалентное условие m —— j . В системе уравнений (26) отношение M T S / M T = 1/ a d показывает, во сколько раз интенсивность входного потока в любом узле больше его пропускной способности.

Очевидно, чтобы уменьшить число теряемых вызовов, количество каналов m должно быть сравнимо с 1 / a d .

Введем параметр p * - 1 - m a d . Здесь всегда p * <  0 , что означает, что система полностью загружена, если же p * >  0 - система недогружена.

Введем случайную величину ^ = т ^Т та кую, что м _; = (1 - р *) ₍ – момент с номером т. Обозначим M р = M , 1 <  Р <  2 ;

-

p (t) = Me ^{- tr} = J e ^{- tmax} P( т ^l )d % ;

r(t) = (1 - 1)[1 - ф (t)]/t ф (t).

Утверждение 3 – это способ определения минимальных потерь запросов в системе. Докажем утверждения 1-3 по методике [2]. Для доказательства используем известные в теории массового обслуживания соотношения для вероятности отказа обработки в канале [3]

Определим вероятность отказа в выполнении обработки как:

^P = ^P m = ^{lim P(}q k = ^т).

к —»

Тогда:

• 1.    Если р * >  E ( e - любое, не зависит от n ), при т — » и E >  0

• 2.    Если M р <  C ( С – не зависит от n ), то последнее соотношение справедливо и в том случае, когда р * —— 0 , но так, чтобы р * Щп ~ V , M = M 2 /2 <  C ;

• 3.    Если р _т * ^Р 1)/ ^Р—» , 1 <  Р <  2 , то

P ~ р * ;

^P = I A j

А-1

)

P ~ V M /2Пт exp(--)Ф 1 ( -vPm ) ~

2M

- 1

р * ф( vvM )

V

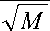
Ф

V

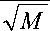
где Ф – функция нормального распределения с параметрами (0,1) .

Используя утверждение 3, можно показать, что если существуют моменты более высоких порядков, то для них существуют соотношения, аналогичные утверждениям 2 и 3. Физический смысл этих утверждений следующий.

Если р < E , то это означает, что все рассматриваемые узлы системы на данном маршруте загружены и практически не простаивают. Очевидно, что за достаточно большое время эти узлы успевают обработать примерно mt / М т ² запросов. Доля необработанных запросов составит

(t/м Т ) - (^/Мт⁸) = 1 _- тМ Т t/м Т        м Т

= 1 - md a = р ,

Смысл утверждения 2 состоит в том, что при

р т ~ V число свободных узлов (нормированных величиной P m ) ведет себя во времени как некоторый диффузионный процесс с отражением, аналогичный рассматриваемому в системе ”гибель-размножение” [3]. Причем для этого случая в соответствии с общим результатом [2] возможно применение для расчета параметров узлов формул в явном виде.

где A = 1 ; A = ( ^m ) j ^{1 - ф (k/m)} ;

• ^'L1 ф (k/m)

ф = M exp( -ат¹_к ) , j = 1,..., т.

Рассмотрим отношение двух соседних слагаемых в соотношении (27)

r = A = т - j + 1 , 1 -(•/тп) • A j - 1 j     ^ф.н'^т)

=,[2 'f;+ vт)^

1 ) -----• . (28) ^т-J )

Из (28) следует, что функция ,(t) регулярна в интервале b(0,1] , непрерывна при T = 0 , ,(0) = 1 — р * . Покажем, что Г ( t ) монотонна при р * >  0 .

Учтем, что на интервале (0, 1] r ( t ) <  1 . Это следует из того, что r (0) <  1 , а уравнение ф (t ) = 1 - t , эквивалентное в области t>0 уравнению r ( t ) = 1 , не имеет положительных решений. Функция ф (t ) выпукла вниз. Поэтому в равенстве [ 1 — ф (t)] /1 = ~(р'(t) в диапазоне 0 выполняется монотонность Т = Т(t). Кроме того, - ф' (Т) также монотонна и

- р ' (t) <  -ф' ( т ) = ¹—^{ф (}-⁾ <  ^P (^t) ;

t 1 - t

'

т -2 = ^{- p (t)}- (1 - ^{t) p} ' ^(t) <  о.

_p (t) J           p (t)

Таким образом, r ( t ) - произведение двух монотонно убывающих сомножителей.

Такое же заключение можно сделать о функции r1(t) = (1 -1)[1 - p1(t)] /tp1(t)

при р *1 = 1 — М^1 > 0 , где ^1 = (т + 1)^/т; р 1( t) = Me-t^S'.

Очевидно, что отношение r j может быть записано в виде

rj = г1(//п + 1).

Для вычисления суммы (27) учтем, что мр = MI < C ; 1 < р < 2;

( р * т) ^р " 1)/^р — 0.

Тогда M ^ <  C ; ( p * m) ^В 1)/^В — ^ r ₁ (1) = 1 - p * + 1 ^В ~ * M(t) ,

где 0 >  M ( 1 ) > — C при 0 <  1 <  1 .

Имеем:

X 1 — ^(k/m)   j/m 1 — ф(1) , ln П--=m m J In—dl+Ldt + k=1 ^(k/m)      0     ф(1)

j ln Aj = Z ln r k=1

( Jk1 j

*

J^{ln(1 —} P 1 ) + E jm .

( J к ^j/m I / Г ( A

У ln^k — m ln1d1 I + - В I ^J I — B(O) I

( k = 1 ^m 0     ) ^ L ( ^m )

равномерна по j .

+ O(1)

Случай lim sup p * = 1 исключается, и m —^

поэтому

|e _jm\ < Cj ^B /m^B"¹ <  C [ m^B" 1 (p*)"^В^ / m ^{B — 1} — 0 .

Используя (31) и j/m

B(o) = lnM^1 ln(J!m—j) — m Jln1d1 = lnj2nJ + Rj, находим

Тогда ;

mm,,

Z ^A j <  Z ^{(1 —} Pi) < ⁽¹ - Pi^)Jo/ Pi .

^j = ^j 0 ^{+ 1     j} = ^j 0 ^{+ 1}

J о           j о                           1  /1    rx y⁺ j 0

Z Aj =Z (1 — P1 )jeEjm = ( pi ) [1 + O(1)] .(29) j=0      J=0

**

Учитывая, что j ₀ ln(1 — p ) <— j p =— ( m ^Bp 1 ) —^ ,

Получим

m

Z A j = —[1 — O (1)] = —[1 + O (1)] . (30)

J = ⁰       P 1                P 1

При p * >  E (30) может быть получено как следствие (29) и того факта, что r_j ~ 1 — p * при j / m —— ^ . Таким образом, утверждение 1 доказывается.

Для доказательства положений 2 и 3 введем m интегральное представление для суммы ZAJ.

J = 0

Имеем

(m I         mj

№. - I = Ф --- ^{— Jln}- - ^(m - An¹~) ⁺ R m ^{— R} J ^— R m — J =

(J)   \2(m——1)m m m jm .—t(31)

=lnJTp “ + mj ln—dtARm — RJ — Rm—J, U 24(m—j) 0 1 J J где Rn — остаточный член в формуле Стирлинга для ln n!. Тогда ln j^1 -qkkmm) k=1 ^(k/m)

-Zn ¹ - (k/m")

_k = 1 (k/m)^k/m)

+ Z n(k-Zm) .

k = 1

Функция D(1) = In{[1 — ^(1)]/1^(1)} имеет на (0, 1] непрерывную и ограниченную производную ^' (0) < C. Поэтому равномерна по k функция m J B(1)d1=B(k/m)—1-В’(к^т)+O(1/m)

(k — 1)/m                   ^2m

В этом случае lnA. = L ln________1 — ^(j/m)_________

^J 2 (j/m)(1 — j / ") ф ( j / m)M ^ + m^JJ J lnr(1)d1 + o(1) — R_{m —} ^ .

Потенцируя, получаем

A j = C(j/m)e^m,(-'^m'[1 + o(1) — R m J . (32) где A j равномерно по j = 0,1,..., m — 1.

В (32) обозначено

C(1) = A-At) ME_E ;

1 — 1

r

J(1) = J lnr(u )du

При j = m находим

A m = , 1 2 A ^L -^{Ф (}1 ■ e ^mJ(1) • [1 + o(1)] . (33) \   Ф( 1)M e

Обратимся к (27). Пусть M _E = 1 — p * >  1 . Тогда ф (o) < — 1 , и уравнения ф ( 1) = 1 — 1 , r( 1) = 1 имеют единственный положительный корень д >  0 . Тогда Ц - точка максимума функции J ( 1 ) , так как

J'(t) = lnr( p ) = 0;

J" ( ц ) = r( p ) = — [1 ф (( ( )])/ / Цф. Ц ) <  0.

При этом ф ( ) ) будет близка к -1, когда p * мало. При p * — 0

) = — 2 p */M ² ^+ o( p *) =—p */M + o( p **) ;

J"( ) ) = — M + o(1).             (34)

J " ( ^ ) равномерно ограничена сверху отрицательной постоянной. Других экстремумов

J(t) не имеет на интервале (0, 1). Поэтому при £1 > 0 и £ > 0 J(t) < J(Ц) - £1 вне интервала (Ц - £, Ц + £), принадлежащего (0,1]. Из ограниченности M следует, что при некотором C > 0 ф(1) > C и ц < 1 - C . Поэтому для любых £, B, удовлетворяющих неравенствам 0 < b < Ц — £ и Ц + £ < B < 1, имеем m       Bm

2 Aj = 2 C(j/m)e^mJ<>'">[1 + o( 1)]. j = ⁰       j = ^bm

Используя метод Лапласа для вычисления этой суммы m J\(t)C(t)mmJ(t)dt = C(j/m)emJ(j/m)[1+o(1)], j/m где h(t) = J'(t)[eJ'(t) - 1]-1.

Тогда

Bm       B

2 A j = m J h(t)C(t)e ^mJ0) dt[1 + o(1)].

j = bm         b

При Ц> £

P ^{— 1} = mC( Ц )e^{mJ( Ц )}       _т      - [ 1 + 0(1) 1.

у m/ J" ( Ц )

При ц — 0 ( p ^a — 0)

P ^{— 1} = mC ( о ) e ^{( Ц} ) I    2 ^    - Ф [ Ц m | J "( ц ) J.

\ m IJ "( ц )

Используя равенство (34) и C(0) = 1 ,

J( p ) = ц 1п(1 -p* ) -Ц м/2 + o( ц ) = ( pj 2M + o[(*] .

Если - p * д/m —— то , то

P ^{- 1} = V 2 ^ m/Me^{mJ( Ц}) [1 + o(1)].

Остался случай M £ <  1 , M d — 1 .

Здесь

P ^{- 1} = m £ h(t)C(t)e^mJ()dt[1 + o(1)].

Обозначая через J"(o) = -D2, J'( o) = -a* D2 < 0, получим mJ (t) = - 2[D)t) - 2J'(o )t + mt2£(t)] = mD 2        2   mD 2 (a*)2     2

= 2— (t + a *) +---- 2 —-— + mt £ (t);

где £ ( t ) —— 0 при t —— 0 . Тогда, учитывая, что изменение N —— то настолько медленное, что N ² £ (N /4m ) — 0 получаем

P^‘4mexp[nD(a^ff /2]{ ТО exp - D 2 u²/2)du + ^ J ' m ^xp/rDU u /2 + a *4m                  a *4m + 2N

+9~p= a * | ( u -a *jm ^dh] } - [1 + o(1)],

V 4m )

где во втором интеграле (u >  a * 4m + 2N)

- Du- -£uh-a * ^ ( u -a *4m ) 2 <- D ( a * V m + N ) " - D ( u -a *4m - 2N ) "

2    V 4m )        ' 2^X 4                   ^Л

Учитывая, что

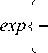
-y(a*4m + N)²

= o \~4r^exp \a *Jm

mD⁾( a *)⁾

окончательно получим

P ^{- 1}

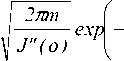
m[J'(o)]⁾ ) Ф J'(o)4m

^2J'(o) ) J^jo^

[1 + o(1)].

В частности, при p * ~ V 4m ,

V > o[J'(o) = ln(1 - p*), J"(o) = M + o(1)], получим

P ^- i = 2 т п    v 2 /2М)ф [ — K= | [1 + o(1)].

V M            V V M )

При p * 44 —— то в соответствии с предыдущим         m( a *) 2 —то и

P ^- ~ 1 / a * D ~ 1 / p* положения 2 и 3 доказаны.

На основании вышеизложенного можно сделать следующее заключение или выводы, что анализ параметров процесса в узле САПРТЭП и полученные зависимости в виде математических моделей показывают, что при работе узла в режиме большой нагрузки, его параметры связаны линейными зависимостями и этот результат позволяет резко упростить вычисления вычислительного комплекса системы САПРТЭП авиационного производства, а для определения предельных характеристик процессов в сложных информационных узлах САПРТЭП необходимо и достаточно вычислить сумму потоков, их распределение по очереди в обработку с использованием метода Лапласа и выравниванием функции Д(t), и определением максимума функции J(t) с положительным корнем m > 0 .