Разработка и исследование алгоритма комплексирования носимого радиомодуля угломерно-дальномерной сверхширокополосной локальной навигационной системы с расширенной базой, инерциального измерительного блока и магнитометра

В настоящее время практически не осталось сфер деятельности человека, в которых не возникала бы необходимость в применении навигационных систем. Одним из методов позиционирования являются глобальные навигационные спутниковые системы (ГНСС) [1], обладающие обширным спектром применения для навигации потребителей военного и гражданского сегментов. Несмотря на постоянный рост требований к характеристикам ГНСС в каждом из упомянутых выше сегментов на фоне технического прогресса, они используются, как правило, для решения задач позиционирования на открытых пространствах. Однако спутниковые радионавигационные системы имеют ряд недостатков, не позволяющих использовать такие системы в ряде практических задач. К наиболее существенным недостаткам можно отнести снижение точности оценок координат из-за эффекта многолучевости, вызванного переотражениями сигналов в условиях плотной городской застройки, и недоступность сигналов внутри закрытых помещений.

В связи с этим возникает необходимость создания и развития локальных навигационных систем (далее – ЛНС) [2], способных обеспечить радиопокрытие в условиях закрытых помещений. Наиболее целесообразным выбором для решения задачи навигации внутри помещений являются ЛНС с использованием сверхширокополосных (далее – СШП) сигналов [3]. Данный выбор объясняется прежде всего тем, что СШП-сигналы состоят из пачек сверхкоротких импульсов, тем самым обеспечивая высокую разрешающую способность по времени и высокую точность измерения временных задержек. СШП ЛНС реализуют позиционный метод навигации, и в качестве их недостатков можно выделить относительно высокую стоимость отдельных радиомодулей. Увеличение размера рабочей зоны СШП ЛНС приводит к кратному росту стоимости системы в целом, процедура их развертывания достаточно трудоемка и зачастую требует привлечения высококвалифицированных специалистов и специализированного оборудования.

Организации, которым необходим мониторинг персонала или обеспечение контроля и управления доступом на режимные объекты, имеют запрос не только на высокую точность позиционирования потребителя, но и на ограниченную стоимость развертывания ЛНС без потери качества ее работы. Этого можно достичь за счет использования навигационных систем, в которых каждая из опорных радионавигационных точек (далее – ОРНТ) способна измерять несколько радионавигационных параметров, что позволяет уменьшить количество ОРНТ. В качестве такой системы может выступать угломерно-дальномерная (далее – УД) ЛНС , позволяющая оценивать дальность до потребителя и угловое направление на него.

На практике при использовании СШП ЛНС возникают ситуации, когда или отсутствует прямая видимость между потребителем и ОРНТ, или сигналы вовсе недоступны, что, в свою очередь, вызывает значительные ошибки в оценках координат потребителя или отсутствие навигационного решения. Для борьбы с факторами, описанными выше, прибегают к такому подходу, как комплексирование различных измерительных датчиков [4–7]. Наиболее подходящими источниками измерений для комплексирования являются СШП ЛНС и инерциальный измерительный блок (далее – ИИБ). Такой выбор обусловлен их взаимодополняющими свойствами. ИИБ позволяет выдавать измерения с высоким темпом и малой флуктуационной составляющей погрешности, при этом им свойственен нестационарный характер, а СШП ЛНС, в свою очередь, обладает более низким темпом выдачи измерений, величина их флуктуационной составляющей погрешности выше, чем у измерений ИИБ, и их характер стационарный.

В навигационных системах, определяющих угол прихода сигнала на потребителя на основе фазовых измерений, для повышения точности оценки угла прихода сигнала увеличивают расстояние между антенными элементами (базу антенной решетки). Ограниче-

Разработка и исследование алгоритма комплексирования носимого радиомодуля ...

нием к увеличению длины базы служит появление неоднозначности фазовых измерений. Существует ряд методов по разрешению фазовой неоднозначности: применение угломерных систем с несколькими базами различной длины, применение двухчастотных угломерных систем, применение априорных данных об угловом направлении и др. [8].

Ввиду вышеприведенных факторов задача повышения точности работы УД СШП ЛНС остается актуальной.

Постановка задачи

Рассмотрим постановку задачи комплексирования носимого модуля УД СШП ЛНС, состоящей из данного модуля и одной ОРНТ, с ИИБ и магнитометром, расположенных на борту носимого модуля и образующих три триады датчиков: трехосевой акселерометр, трехосевой ДУС и трехосевой магнитометр. ОРНТ УД СШП ЛНС состоит из двух приемопередатчиков (ведущего и ведомого), тактируемых общим опорным генератором, и каждый из которых подключен к своему собственному антенному элементу. Отрезок, соединяющий эти антенные элементы, называется базой УД СШП ЛНС. Структурная схема УД СШП ЛНС показана на Рисунке 1.

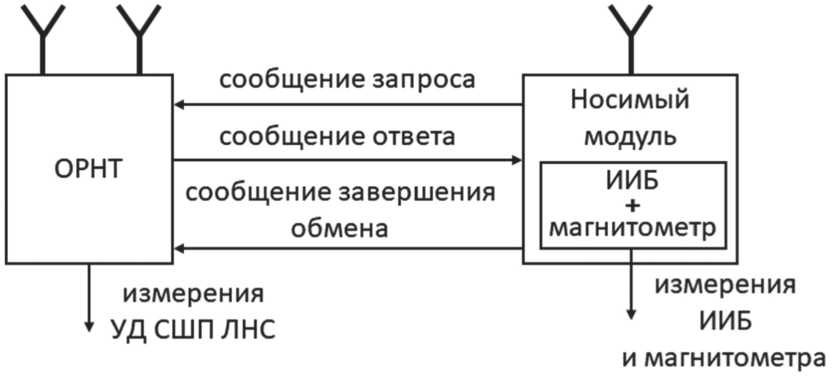
Рисунок 1. Структурная схема УД СШП ЛНС

Источник: здесь и далее рисунки, схемы и диаграммы выполнены авторами.

Как показано на Рисунке 1, измерение радионавигационных параметров в рассматриваемой УД СШП ЛНС производится путем процедуры запросного измерения дальности с повторным ответом (далее – ЗИДПО), и результат измерения формируется на стороне ОРНТ в момент времени t _завпр_мM в шкале времени ОРНТ. Параллельно с процедурой ЗИДПО ИИБ и магнитометр выдают измерения в моменты времени t иив/маг , фиксируемые в шкале времени носимого модуля (см. Рисунок 2).

На диаграмме Рисунка 2 приняты следующие обозначения: tзапрпр^ - момент времени отправки носимым радиомодулем сообщения запроса в шкале времени носимого радиомодуля; tзапрпрм - момент времени приема ведущим приемопередатчиком (далее - ПП) ОРНТ сообщения запроса в шкале времени ОРНТ; tотвпр^ - момент времени отправки ведущим ПП ОРНТ сообщения ответа в шкале времени ОРНТ; tomвпpм - момент времени приема носимым радиомодулем сообщения ответа в шкале времени носимого радиомодуля; tзавпр^ - момент времени отправки носимым радиомодулем сообщения завершения обмена в шкале времени носимого радиомодуля; tзавпрм M - момент времени приема ведущим ПП ОРНТ сообщения завершения обмена в шкале времени ОРНТ; tзавпрмS -момент времени приема ведомым ПП ОРНТ сообщения завершения обмена в шкале времени ОРНТ; Трасп - время распространения сигнала между ОРНТ и носимым радиомодулем; Тотв1 - время ответа ОРНТ на сообщение запроса; Тотв2 - время ответа носимым на сообщение ответа.

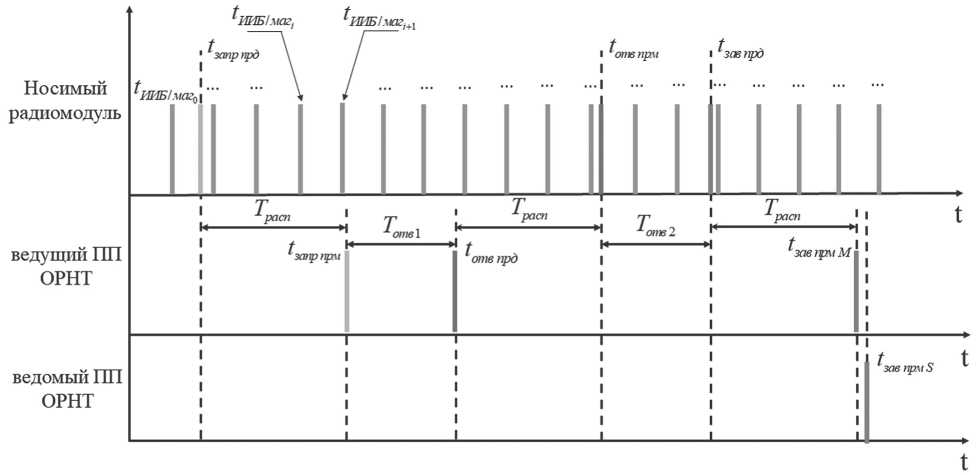
Рисунок 2. Временная диаграмма измерений УД СШП ЛНС и ИИБ

В сообщение завершения обмена закладывается момент времени отправки носимым радиомодулем сообщения t _{зав прд} . Учитывая, что за промежуток времени между отправкой и приемом данного сообщения изменение радионавигационных параметров пренебрежимо мало, можно принять, что эти параметры соответствуют моменту времени в шкале времени носимого модуля. Таким образом, на стороне ОРНТ имеются измерения УД СШП ЛНС, ИИБ и магнитометра в шкале времени носимого модуля.

Пусть имеется потребитель – человек, перемещающийся пешим ходом. На поясе данного потребителя закреплен носимый модуль УД СШП ЛНС, на борту которого расположены ИИБ и магнитометр. Зададимся двумерной правосторонней прямоугольной локальной системой координат (далее – ЛСК), ось x которой образована антенными элементами (базой) УД СШП ЛНС с началом, расположенным в середине базы УД СШП ЛНС. Требуется в шкале времени носимого модуля формировать оценки вектора состояния потребителя xk , на поясе которого закреплен носимый модуль, в ЛСК. Вектор состояния включает в себя 4 элемента и имеет вид xк =[xk Vx, Ук Vy, ]T ,                                  (1)

где x _k и y _k – координаты потребителя в ЛСК; V _x и V _y – компоненты вектора скорости потребителя в ЛСК.

Динамика системы описывается следующими уравнениями:

Разработка и исследование алгоритма комплексирования носимого радиомодуля ...

' xk = x k - 1 + V x_k - 1 ^A T k ,

V k = V X _+^ k ^A T k ,

' y k = y k - 1 + V y k A T k ,                          ()

_ Vyk = Vyk-1 + ^Vyk A Tk, где ATfc - разность моментов времени фиксации радиоизмерений в шкале времени носимого модуля.

В векторно-матричной форме приведенные выше уравнения записываются, как показано ниже:

x k = F k x k - 1 ^{+ G} k ^£ k ,                        (3)

где

£ k - вектор формирующих шумов компонент вектора скорости потребителя с нуле-

2 выми матожиданиями и дисперсиями с ^ и с			2 ^v, ; F k	– переходная матрица; G k		– ма-
трица формирующих шумов.			y
	1 A T k 0   0		■ 0	0 "
	0100		A T k	0	Г ^
F k =	0   0   1 A Tk	, G k =	0	0	xk Л k = ^ V yk .	(4)
	0   0   0   1		_ 0	A T k _

Примем следующую модель наблюдаемых на стороне ОРНТ измерений УД СШП

ЛНС, а именно: дальности Rk от ОРНТ до носимого потребителем модуля, наблюдаемой на фоне аддитивного белого гауссовского шума nR с нулевым матожиданием и дисперсией сП , и разности фаз Aфk принятого ОРНТ сигнала от носимого модуля, функционально связанной с углом пеленга 0к (см. Рисунок 3) и наблюдаемой на фоне аддитивного белого гауссового шума nАф с нулевым матожиданием и дисперсией с^:

R R

Aф k ] = [а ф ^ f n ^radk

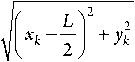
X- sin ( 9 k ) ^{- 2 n M} i_k

n R_k n Aф k

—

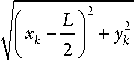
2nL sin

X

2nMj ik

ⁿ R k

. n Aф k

y _k

—

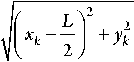
2 n L

X

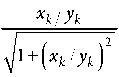
2пМ ik

+

n R_k

. n Aф k

где L - длина базы антенной решетки ОРНТ; 2 = с// 0 - длина волны СШП-сигнала, определяемая как отношение скорости света ñ к центральной частоте СШП-сигнала f ₀ ; M _i – номер i -го сектора однозначности, в котором находится потребитель. Сектором однозначности с номером M _i называется угловой сектор рабочей зоны УД СШП ЛНС, в каждой точке которого измеряемая разность фаз прихода непрерывно изменяется в пределах [–π, π], при этом его номер M _i соответствует числу полных фазовых циклов. Дополнительное слагаемое L 2 в модели наблюдаемой дальности обусловлено тем, что дальность измеряется до ведущего приемопередатчика ОРНТ, смещенного относительно центра базы на расстояние, пренебречь которым, как в случае стандартной базы, нельзя.

Так как носимый модуль закреплен на поясе потребителя-пешехода, то в процессе ходьбы в измерениях инерциальных датчиков наблюдаются характерные “перепады”, соответствующие определенным фазам шага, а значит, целесообразно извлекать из инерциальных измерений дополнительную информацию о проделанных шагах потребителя. Помимо данного факта, стоит отметить, что архитектура исследуемой УД СШП ЛНС предполагает измерение радионавигационных параметров на стороне ОРНТ, поэтому для реализации комплексного алгоритма, совместно обрабатывающего данные упомянутых измерителей, необходимо передавать информацию, полученную с ИИБ на сторону ОРНТ. Очевидно, что энергетически выгоднее передавать не «сырые» измерения ИИБ, выдача которых производится с высоким темпом, а информацию о проделанных шагах, полученную в результате обработки инерциальных измерений.

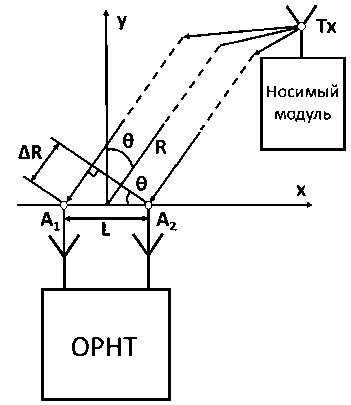
Рисунок 3. Принцип определения угла пеленга θ в исследуемой УД СШП ЛНС

Описанное выше извлечение информации о шаге можно обеспечить применением алгоритмов пешеходного счисления пути (далее – ПСП). Традиционно в системах ПСП расчет пройденной дистанции основан на определении длины и направления пройденных потребителем шагов и вычислении его новых координат на основе найденного перемещения потребителя относительно его предыдущего местоположения. При объедине-

Разработка и исследование алгоритма комплексирования носимого радиомодуля ...

нии оценок алгоритма ПСП с измерениями иных датчиков, позволяющих определять абсолютные координаты потребителя в заданной системе координат, целесообразно перейти от относительных координат к компонентам вектора скорости.

Принимая абсолютное значение скорости и угол курса потребителя на длительности шага постоянными, на такты радиоизмерений имеем оценки компонент вектора скорости алгоритма ПСП, являющиеся наблюдениями для разработанных алгоритмов ком-плексирования УД СШП ЛНС и ИИБ:

У к =

_

^V x псп_к

_

V y псп к

^V x ССП,

^V y псп,

k

k

_

^V пcп

V ncn_t ^cos ( ^У пcП k )

^сп_к sin

+

n

(У   ) n

У псп к /J ^L

V x псп к

1V

V y псп_к

,

где n ^_

V x псп_к

и n у   - аддитивные белые гауссовы шумы с нулевыми матожиданиями

У ссп_к

и дисперсиями ст ,^_    и ст ,^_    .

^V x спп       ^V y спп

Расчет дисперсий оценок компонент вектора скорости потребителя на выходе алго-

—

ритма ПСП ст V и ст V производится на основе выражения для оценки дисперсии случайной величины, являющейся функцией нескольких независимых случайных величин:

_

V x псп

= (VПCПk cos (Упспк ) V cos У пспк /

‘

^{7 V}ПCП k_i у v '

^V пcп

( ^V ПCП k ^cos ( ^w пcп k

V

‘

^У псп к у

V ст 2

^У псп

г

шаг

ст

^{Д L} пcп

+

( ^V ПCП k

I ^{ст 2} ;

^У псп

--

V y псп

= ( ^V пc:п_l V

sin У j

У пспк /

^{7 V}ПCПk_i у

^сп

г,

( V с.

V

^У псп к у

ст ²

^У псп

т

шаг

ст

^{Д L} пcп

V cosl у ст , ^{сп к}    У ^псп к       У псп

где ^ст Д Lпcп

ПСП, т

и

ст ²

У

псп

– дисперсия оценок длины шага и угла курса на выходе алгоритма

– длительность шага.

В зависимости от уровня совместной обработки данных измерителей и качества обеспечиваемых характеристик выделяются следующие схемы комплексирования: глубокоинтегрированная, тесносвязанная, слабосвязанная и разомкнутая. Ввиду того что в исследуемой УД СШП ЛНС измерение радионавигационных параметров производится на стороне ОРНТ, но требуется оценить координаты носимого модуля с ИИБ на борту, наиболее предпочтительным вариантом, который возможно реализовать в данной постановке задачи, является слабосвязанная схема комплексирования .

Исходя из изложенного выше, можно предложить следующую обобщенную структурную схему комплексирования УД СШП ЛНС и ИИБ, алгоритмы для которой разработаны и исследованы в данной работе (см. Рисунок 4).

На вход алгоритма ПСП поступают компоненты вектора ускорения потребителя a от трехосевого акселерометра, вектор угловых скоростей ^_ от ДУС и компоненты векто-

ра магнитного поля m от трехосевого магнитометра в ССК. На выходе алгоритма ПСП формируются оценки компонент вектора скорости потребителя V ^ˆ _x   и V ^ˆ _y   в ЛСК.

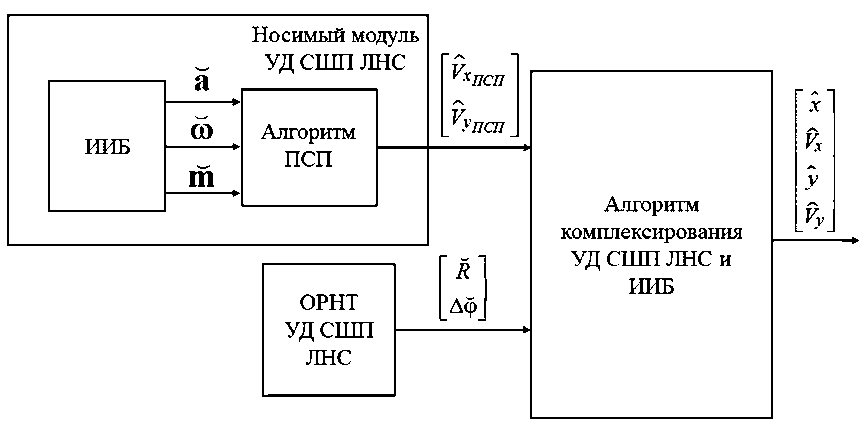
Рисунок 4. Обобщенная структурная схема комплексирования УД СШП ЛНС и ИИБ

На вход алгоритма комплексирования носимого радиомодуля УД СШП ЛНС, ИИБ и магнитометра поступают измерения дальности R от ОРНТ УД СШП ЛНС до носимого потребителем модуля, разности фаз прихода сигнала ∆ ϕ на антенные элементы ОРНТ УД СШП ЛНС и оценки компонент вектора скорости потребителя V ^ˆ _x и V ^ˆ _y в ЛСК от алгоритма ПСП. На выходе алгоритма комплексирования УД СШП ЛНС и ИИБ формируются оценки координат потребителя и компонент его вектора скорости в ЛСК.

Разрешение фазовой неоднозначности

Как известно, однозначное определение угла пеленга на потребителя для однобазовых УД ЛНС возможно лишь при длине базы меньше половины длины волны сигнала. В случае расширенной базы для каждой пары измерений разности фаз прихода сигнала и дальности до потребителя существует несколько возможных местоположений потребителя. Данное явление называется проблемой фазовой неоднозначности, а ее решение, соответственно, разрешением фазовой неоднозначности [9]. Таким образом, возникает необходимость сформулировать критерий завязки траектории потребителя УД СШП ЛНС с расширенной базой, ИИБ и магнитометра.

В данной работе для завязки траектории используется информация от алгоритма ПСП о курсе потребителя и набор измерений дальности и разности фаз от УД СШП ЛНС на временном интервале шага. В моменты времени t _k поступают измерения УД

^-

СШП ЛНС R _k и ∆ ϕ _k , и ∆ T_k = t_k - t_{k - 1} – темп поступления этих измерений. В моменты времени t _Ha4mo и t _K0H eu, алгоритм ПСП сигнализирует о начале и конце шага соответственно (см. Рисунок 5). Длительность шага может быть различна, поэтому различное количество измерений УД СШП ЛНС может поступить в интервале шага.

Разработка и исследование алгоритма комплексирования носимого радиомодуля ...

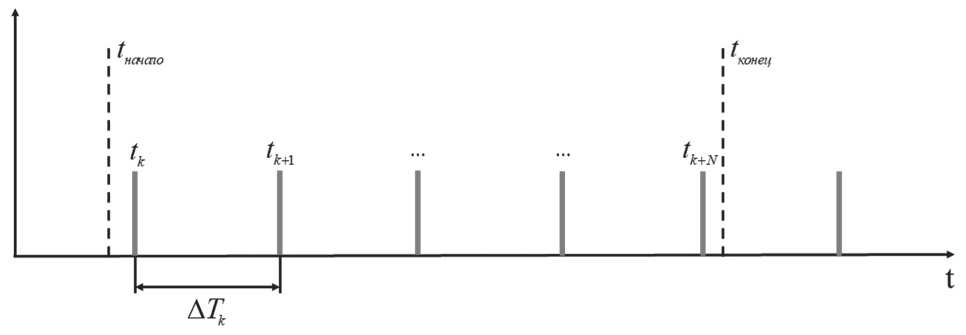
Рисунок 5. Временная диаграмма к пояснению разрешения неоднозначности

^^                                                       ^^            ^^

Сначала объединяются в наборы R ^ k ₊ n , A P      измерения R ^ , ... , R ₊ n ; A p

К. . .К + .N                                                К

,..., Ap ^ + n , поступившие в моменты времени t ^ , .„, t ^ ₊ n , на временном интервале шага с момента времени [ t,^^, , t _K0He4 ] . Затем набор истинных измерений разностей фаз A( p m к ₊ N , значения которых лежат в интервале 0 — А ф ^ ^ +. <  2 п , j = 0, N , пересчитываются в возможные значения, если бы реальный сигнал приходил с соответствующих угловых направлений:

A p m + j - A p _{fc + ;} . + 2 n m i , j = 0, N , i = 1, K ,

где mi , i = 1, K - i -й номер сектора однозначности, в котором возможно нахождение траектории потребителя, принимающий целочисленные значения

m =

-

K - 1 K - 1 1

...

...

,

где K – количество секторов однозначности, определяемое как K- 2 | L - mod ( L ||+ 1.

■^^

На следующем этапе набор полученных на предыдущем этапе значений R ^ k ₊ N , A p ^ m i к ₊ N переводится в прямоугольные координаты.

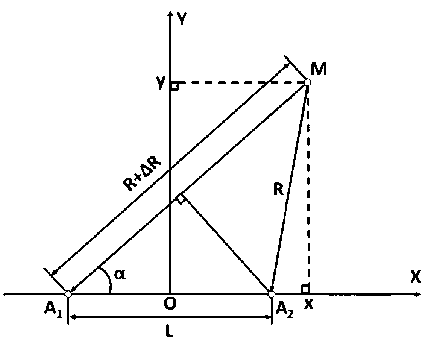
Рисунок 6. К выводу формул для перевода дальностей и разностей фаз прихода сигнала в прямоугольные координаты

Из ΔA1A2M по теореме косинусов получаем cos(a) — ——1—— [(R + AR)2 + L2 — R2 .

V ' 2 ( R + AR ) L

Из AA 1 x M выражаем cos ( a ) как

, _x x + L 2 cos ( a ) —------- ^R + ^{A R}

Объединив (12) и (13), получим x + L/ 2       1

------— — ------- — I ( R + A R

R + A R 2 ( R + A R ) L V

.

² ) ,

x —

) ² + L 2 — R ² ) — L = ~ ( ² R A R + A R ² + L ² ) — L =

R A R A R ² A R C A R )

11 R +I .

L 2 LL

С учетом найденного x из ΔA₁ x M по теореме Пифагора выразим y :

У =

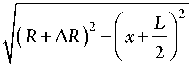
m

Используя выражения (14) и (15), для наборов a ® , + .,

i = 1, K , j — 0, W и R , + j j — 0, W

рассчитаем наборы значений x ^+j , y km i j , m i — 1, K j — 0, W в соответствии с выражением

- m i ^xk„. k + W

= a® — + w

2 n L

A< ® m : k + W-x )

R ^k - ^{k + W +}     4 п     I ;

- mi    = yk - k+W

D     ₊^A ® k l k + W

R ^k - ^{k + W} +    2 n

—

- mi      L xk - k+W + 2

.

Далее для оценки направления шага в каждом секторе однозначности для наборов каждой из рассчитанных координат применяется метод наименьших квадратов (далее – МНК) из класса численных методов. Для каждого значения m i , i — 1, K берется набор значений X m + j , j — 0, W , то есть для интервала времени [ t _k , t _{k + W} ] , который аппроксимируется прямой линией k m' ( t_k + j A T_k ) + b m , j — 0, W , параметры которой k m , b m i определяются таким образом, чтобы минимизировалась квадратичная форма J — £ ( x + j — ( k m ( t k + j A T k ) +b m ) ) ² , аналогичная процедура проводится для y mj , j — 0, W . Входные параметры для МНК X m i _{k + W} по координате х и соответствующие этим координатам моменты времени t_{k k + W} .

Затем определяется направление шага во всех возможных секторах

С m i

^Щ мнк •

однозначности

К т^

С м»™ = atan2 , kxm i v x

mi

)

, i — 1, K .

I

mi

Следующим этапом является составление набора модуля невязок Щ _мнк — V псп

mi

~

меж-

ду углами наклона линии (в плоскости), вдоль которой делается шаг, по измерениям УД

Разработка и исследование алгоритма комплексирования носимого радиомодуля ...

СШП ЛНС /КнК и углом наклона данной линии, оцененным алгоритмом ПСП /псп . В конце процедуры устранения фазовой неоднозначности применяется МНК, составля- mi ется набор значений Кмнк —/псп

для набора mi, i = 1,K , который аппроксимируется кривой второго порядка (параболой) (ami + bmi +c), i = 1,K , параметры которой a, b, c определяются таким образом, чтобы минимизировалась квадратичная форма. Таким образом, минимизируемый функционал можно записать в виде

2.,^2

( am i ² + bm i +c ) 1 . Выбранный порядок аппроксимируемой

N

J mi

= Х ( Кмн к ^—/ псп ^—

j=о mi функции обусловлен характером зависимости найденного вектора невязок / мнк-/псп от номера сектора однозначности mi (см. Рисунок 7).

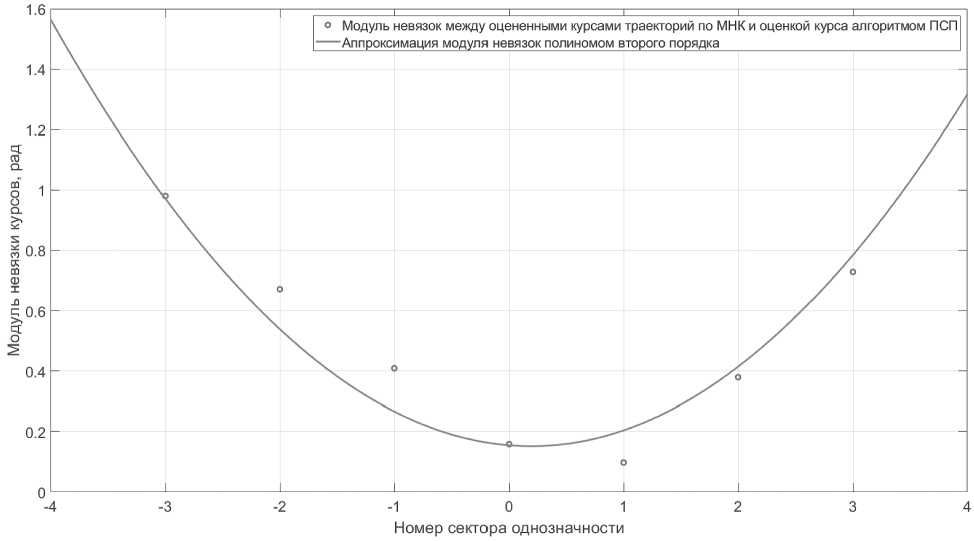
Рисунок 7. Вид зависимости нормы

^ m i   ^

V КНК ^ псп

от номера сектора однозначности m i для l/ X = 0.5

Оценка номера сектора однозначности, в котором лежит траектория потребителя mi , определяется как

л mi

= round

argmin ( a m2 + b mi- +c ) .

m _i

Разработка алгоритма

Одним из вариантов решения задачи комплексной фильтрации, постановка которой представлена в предыдущем разделе, является расширенный фильтр Калмана (далее – РФК) [10]. Известно, что фильтрация процессов в гауссовом приближении (калманов-ская фильтрация) при нелинейной модели наблюдения позволяет квазиоптимально оценить интересующие параметры объекта.

Подход линеаризации, используемый в РФК, не всегда корректен и может привести к значительным ошибкам в аппроксимации. Известен ряд альтернатив этому методу, одной из которых является сигма-точечное преобразование (далее – СТП). В основе СТП лежит численный алгоритм определения нескольких начальных моментов многомерной функции плотности вероятности (далее – МФПВ) случайной величины после ее нелинейного преобразования. Для этого МФПВ до преобразования описывается детерминированным набором сигма-точек, что позволяет после преобразования однозначно восстановить необходимые моменты МФПВ. Основным требованием к преобразованной МФПВ является ее симметричность и унимодальность. Таким образом, сигма-точечный фильтр Калмана (далее – СТФК) [11] представляет собой алгоритм фильтрации на основе СТП.

СТФК, как и РФК, состоит из двух основных этапов – экстраполяции и коррекции. Единственным отличием алгоритма РФК от СТФК является то, что указанным этапам теперь предшествует процедура выбора сигма-точек.

Чтобы гарантировать положительную полуопределенность матрицы дисперсий, целесообразно реализовать вариацию СТФК с квадратным корнем из матрицы дисперсий шумов фильтрации (далее – КК-СТФК) [12]. В данной вариации СТФК в начале каждой итерации выбирается набор из (2 N + 1) сигма-точек (где N – число элементов в векторе состояния) в соответствии со следующими выражениями:

% 0 - 1 = x k - 1

х k - 1 = x k - i + (7 ^{( N + к )} S k - 1 ) , i = 1... ^N ;

л xk-i=xk-i (7(N+к)Sk-i)., i=1...N, где ( 7 (N+к)Sk-1) – i-я строка или столбца квадратного корня из взвешенной ковариационной матрицы 7(N + к)Sk-1 и к является параметром масштабирования, который предлагается (3 – N). Веса сигма-точек для оценки среднего значения и дисперсии их распределения определяются как

W ( m ) = _L_ .

⁰ N + 2

W ( m ) =   ² + (1 - a 2 + в).

⁰ N + 2

W(m) = W(c) = ——----, i = 1...2 N, i i    2( N+2)

где a - коэффициент, отвечающий за разброс сигма-точек относительно матожидания x k ; в - коэффициент, учитывающий влияние членов высоких порядков (выше второго) разложения в ряд Тейлора матрицы дисперсий (для гауссова распределения выбирается равным 2); 2 - масштабирующий параметр, определяемый в соответствии с выражением

2 = a ² ( N + к ) - N ,                              (21)

где к - вторичный масштабный коэффициент, обычно выбираемый равным 0.

Затем все выбранные сигма-точки x k _{- 1} распространяются в соответствии с моделью динамики системы, и по ним вычисляется экстраполированный вектор состояния x k и квадратный корень из матрицы дисперсий S _k :

Разработка и исследование алгоритма комплексирования носимого радиомодуля ...

X k = Fx k - 1 ;

x k = Z W ( m ) i k ;

j = 0

S k = qr ^f V W F (% k ^{- x} k ) 7Q ) , ^j = ¹™^{2 n} ;

S k = cholupdate ( S k , (% ^{0 -} x k ) , sign { ^w( c ) } V ^w( c )

где qr(*) – QR-разложение матрицы; cholupdate(*) – малоранговая модификация квадрат- ного корня из матрицы; Q – квадратный корень из матрицы дисперсий формирующих шумов, которая определяется с помощью разложения Холецкого как

VQ = chol ( GD^G T ) .                             (23)

На следующем этапе экстраполированные сигма-точки преобразуются в соответствии с моделью наблюдений:

y k = h ( X k ) ;

y k = £ W ( m ) y k ;

j = 0

S y _k = qr ^f V W /c ) ( ^y k ^{- y} k )   TD n ^ , j = 1...2ⁿ ;

S y k = cholupdate ( S y _k , ( ^y 0 ^{- y} k ) ,sign { W^{( c} ) } ^W j ^c ) ) .

Следующий шаг КК-АФК заключается в определении матрицы кросс-ковариаций

D _xy и матрицы весовых коэффициентов фильтра K _k :

2 n                              T

j = 0

K k =

f )

D x k y k

S T

V    y k Л

f~

S y. .

y _k

В конце итерации алгоритма находятся оценки вектора состояния x ^ˆ _k и квадратного

ˆ корня из матрицы дисперсий шумов фильтрации Sk :

^x k = ^x k + ^K k ( y k -y k ) ;

S k = cholupdate ( s k , K k D x _k y _k , ^{- 1} ) .

Алгоритм формирует оценки вектора состояния в такты радиоизмерений. Вектор на- блюдений yk формируется в зависимости от того, детектирован ли шаг на данный момент времени. Если алгоритм ПСП сигнализирует, что на данный момент времени потребитель совершает шаг, то в состав данного вектора входят радиоизмерения от УД СШП ЛНС (5) и оценки алгоритма ПСП (6):

[ '^-’                            '^-’                       '^-’                   T

R k ^9 k V_x ncn_k V y ncn_k J .

Если в данный такт радиоизмерений алгоритм ПСП не детектирует шаг потребителя, то полагаем, что потребитель в данный момент неподвижен и вектор-столбец невязок:

[ 2.-                             ^,^-’            ^,^-’        T

R k ^Ф к   V x_k   V y_k J .

В выражении (28) под V x и V y понимаются псевдоизмерения компонент вектора скорости потребителя, выбираемые близкими к нулю, так как отсутствие сигнала о факте шага от алгоритма ПСП свидетельствует о том, что потребитель неподвижен.

Результаты имитационного моделирования

В имитационном моделировании исследовалась точность оценок координат потребителя разработанным алгоритмом комплексирования носимого радиомодуля УД СШП ЛНС с расширенной базой, ИИБ и магнитометром.

Потребитель в проведенном имитационном моделировании прошел по траектории, имеющей форму прямоугольника размером 5,7 × 4,5 м. Условия моделирования данной траектории: пройденная дистанция – 32 шага, общая длина траектории – 20,4 м, общая длительность измерений – 25,5 с, модуль вектора скорости – 1 м/с, угол курса потребителя и модуль вектора его скорости на временном интервале шага оставались постоянными. Остальные параметры были следующие: темп радиоизмерений T = 0,1 c; СКО формиру- ющих шумов су = Су = 1 м/с2; СКО шума наблюдений от УД СШП ЛНС

V _x V _y

C r = 0,03 1 , с _Д ф = 6 ° , длина базы: L = 4 2 .

Дисперсия шумов наблюдений компонент вектора скорости c VV ритма ПСП рассчитывается на каждом такте с помощью выражений (7)

г ²    от алго-

^V y ПСИ

и

и

Для описанных условий было проведено имитационное моделирование работы пред- ложенных алгоритмов комплексирования носимого радиомодуля УД СШП ЛНС с расширенной и стандартной базой, ИИБ и магнитометром. Оценки координат упомянутых выше алгоритмов показаны на Рисунке 8.

Ошибки оценок координат разработанных алгоритмов комплексирования носимого радиомодуля УД СШП ЛНС с расширенной и стандартной базой, ИИБ и магнитометром продемонстрированы на Рисунке 9.

Из результатов проведенного имитационного моделирования следует, что увеличение длины базы ОРНТ УД СШП ЛНС в 8 раз позволяет алгоритму комплексирования носимого радиомодуля УД СШП ЛНС с расширенной базой, ИИБ и магнитометром при заданных характеристиках измерителей достичь РСКП оценок координат потребителя менее 3 см, что более чем в 2 раза ниже РСКП оценок координат алгоритма комплексирова-ния носимого радиомодуля УД СШП ЛНС со стандартной базой, ИИБ и магнитометром.

Разработка и исследование алгоритма комплексирования носимого радиомодуля ...

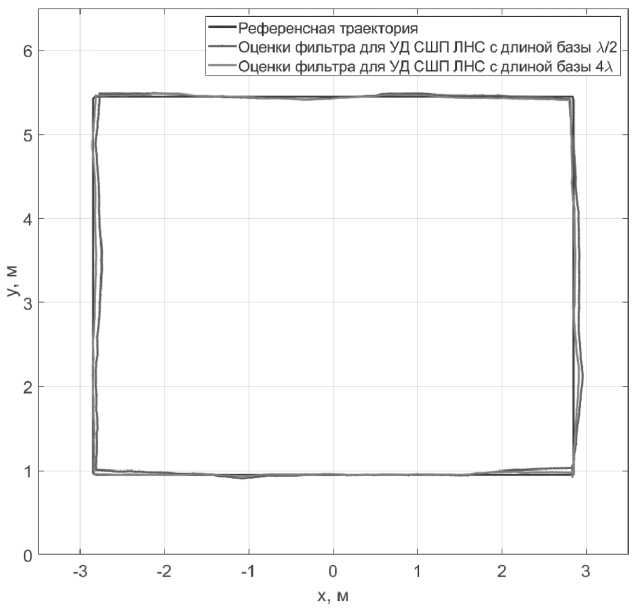
Рисунок 8. Траектория, оцененная разработанными алгоритмами комплексирования носимого радиомодуля УД СШП ЛНС со стандартной (λ/2) и расширенной (4λ) базами, ИИБ и магнитометра в имитационном моделировании

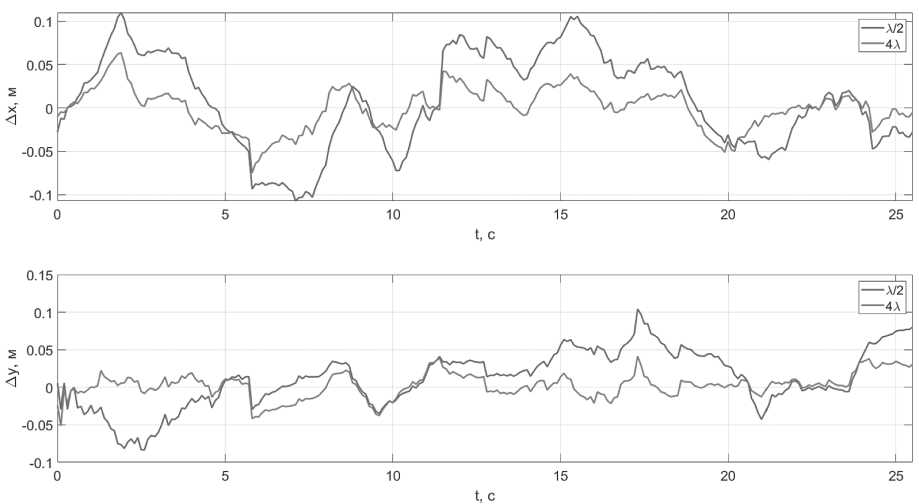
Рисунок 9. Ошибки оценок координат разработанных алгоритмов комплексирования носимого радиомодуля УД СШП ЛНС со стандартной (λ/2) и расширенной (4λ) базами, ИИБ и магнитометром, полученные при имитационном моделировании

Результаты натурного эксперимента

Для валидации предложенного критерия завязки траектории (18) и оценки точности работы алгоритма комплексирования УД СШП ЛНС с расширенной базой, ИИБ и магнитометром был проведен натурный эксперимент.

В данном эксперименте потребитель прошел по намеченной маркерами прямоугольной траектории размером 5,7 × 4,5 м. Носимый радиомодуль DWM 1003 с ИИБ и магнитометром закреплялся на поясе потребителя. Измерения с ИИБ и магнитометром сначала передавались по UART на плату Raspberry Pi 4 Model B, после чего отправлялись по каналу Wi-Fi на ПК. Радиоизмерения передавались по USB-интерфейсу ОРНТ УД СШП ЛНС, к которому через ВЧ-переключатель подсоединялись внешние антенны, разнесенные на расстояние 4λ (см. Рисунок 10).

Носимый радиомодуль УД СШП ЛНС, подключенный к микрокомпьютерус Wi-Fi модулем

Маркеры, через которые прошел потребитель в ходе эксперимента

ПК для записи и обработки данных от ОРНТ и носимого радиомодуля

ОРНТУД СШП ЛНС с внешними антеннами, разнесенными на 4Л

Апробация алгоритма комплексирования УД СШП ЛНС с расширенной базой и ИИБ в натурном эксперименте

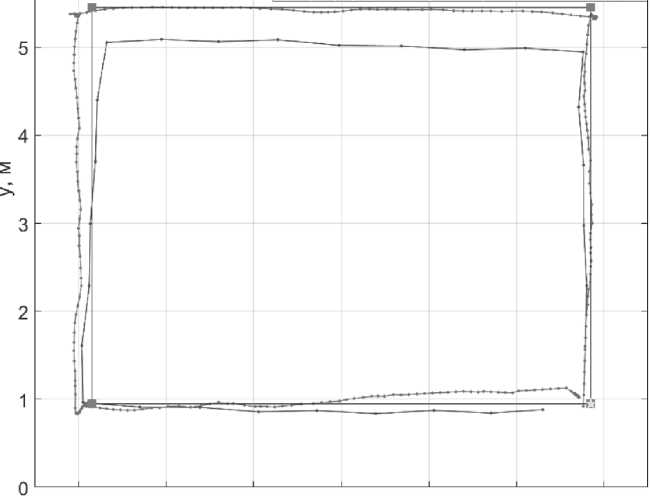
Рисунок 10. Схема натурного эксперимента для валидации и оценки точности разработанного алгоритма комплексирования носимого радиомодуля УД СШП ЛНС, ИИБ и магнитометра Траектории, оцененные алгоритмом ПСП и разработанным алгоритмом комплекси-рования носимого радиомодуля УД СШП ЛНС с расширенной базой, ИИБ и магнитометром в натурном эксперименте, приведены на Рисунке 11.

Ошибки оценок координат разработанного алгоритма комплексирования УД СШП ЛНС с расширенной базой и ИИБ показаны на Рисунке 12.

Результаты натурного эксперимента показали, что РСКП оценки координат потребителя разработанного алгоритма комплексирования УД СШП ЛНС с расширенной базой и ИИБ составила менее 12 см.

Разработка и исследование алгоритма комплексирования носимого радиомодуля ...

Оценки алгоритма ПСП

Оценки алгоритма комплексирования

УД СШП ЛНС с расширенной базой и ИИБ

—■—Референсная траектория Начальная и конечная точка референсной траектории

-3-2-10123

х, м

Рисунок 11. Траектория, оцененная разработанным алгоритмом комплексирования носимого радиомодуля УД СШП ЛНС с расширенной базой, ИИБ и магнитометром в натурном эксперименте

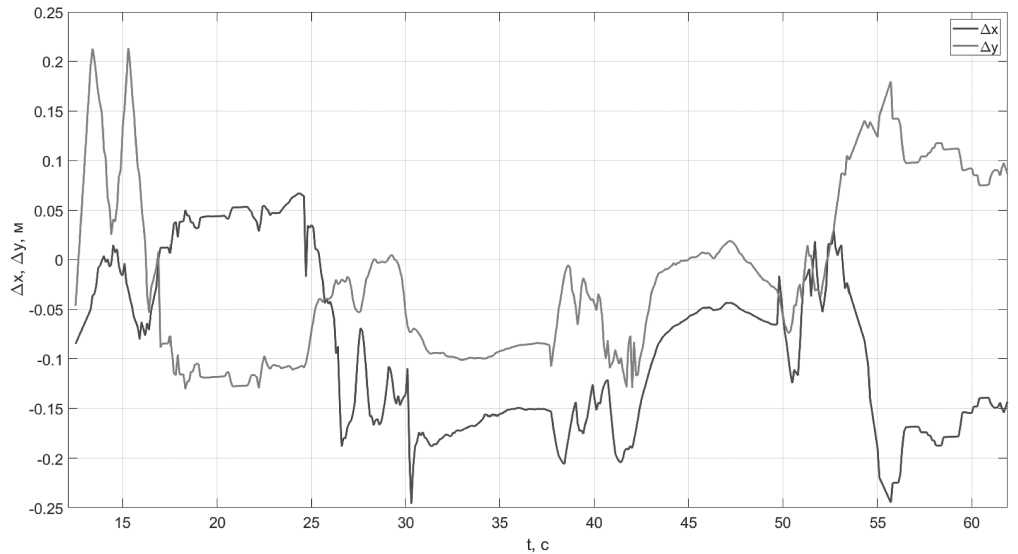
Рисунок 12. Ошибки оценок координат разработанного алгоритма комплексирования носимого радиомодуля УД СШП ЛНС с расширенной базой, ИИБ и магнитометром в натурном эксперименте

Заключение

В данной работе были получены следующие результаты.

Разработан и апробирован алгоритм комплексирования носимого радиомодуля УД СШП ЛНС с расширенной базой, ИИБ и магнитометром, который показал РСКП оценок координат менее 12 см в натурном эксперименте и выигрыш в РСКП оценок координат более чем в 2 раза перед алгоритмом комплексирования носимого радиомодуля УД СШП ЛНС со стандартной базой, ИИБ и магнитометром в имитационном моделировании.

Разработан подход к завязке траектории потребителя УД СШП ЛНС с расширенной базой на основе оценок угла курса потребителя от алгоритма ПСП.