Разработка и исследование энергетических моделей импульсных стабилизаторов напряжения

Импульсные стабилизаторы напряжения (ИСН) широко применяются в автономных системах электропитания (СЭП). Они обеспечивают достижение таких противоречивых требований, как высокие удельные характеристики и высокое качество электроэнергии на выходе СЭП.

Энергетические характеристики ИСН: КПД и минимальное возможное напряжение между входом и выходом ИСН – в значительной мере определяют выполнение энергобаланса в СЭП и срок их функционирования.

Постановка задачи. Энергетические процессы в автономных СЭП в настоящее время целесообразно анализировать с помощью методов компьютерного имитационного моделирования. Это позволяет оценить:

– обеспечение энергобаланса в СЭП при известных энергетических характеристиках основных и буферных источников энергии и временной диаграмме энергопотребления со стороны нагрузки;

– обеспечение энергобаланса в СЭП в условиях деградационных изменений энергетических характеристик основных и буферных источников.

Для проведения такого анализа необходимо разработать энергетическую модель импульсного стабилизатора напряжения, логика функционирования которого соответствует логике функционирования реального ИСН [1], входящего в состав СЭП. Эта модель должна:

– обеспечивать стабилизацию выходного напряжения в номинальных режимах работы;

– обеспечивать ограничения выходного тока на заданном уровне при перегрузке с соответствующим понижением выходного напряжения;

– прерывать процесс стабилизации выходного напряжения при снижении входного напряжения ниже уровня напряжения стабилизации;

– изменять КПД в функции отношения выходного напряжения к входному и в функции изменения мощности нагрузки.

В модели должна быть предусмотрена возможность изменения уровня напряжения стабилизации, точности его поддержания, уровня тока ограничения и отклонения выходного тока от заданного в режиме тока ограничения.

Поставленную задачу можно решить, используя расчет мгновенных значений токов и напряжений [2]. В этом случае исследуется модель ИСН, состоящая из аналоговых элементов: конденсаторов, дросселей, диодов, транзисторов, работающих в ключевом режиме, и т. п. Однако такое исследование может растянуться на несколько десятков часов, что делает его непригодным для анализа энергетических процессов, занимающих значительные временные интервалы. Поэтому целесообразна разработка энергетических моделей ИСН, состоящих преимущественно из функциональных блоков и не учитывающих импульсный характер преобразования энергии в ИСН, что позволяет существенно снизить затраты времени .

Модель импульсного стабилизатора напряжения. Рассмотрим работу энергетической модели импульсного стабилизатора напряжения (рис. 1).

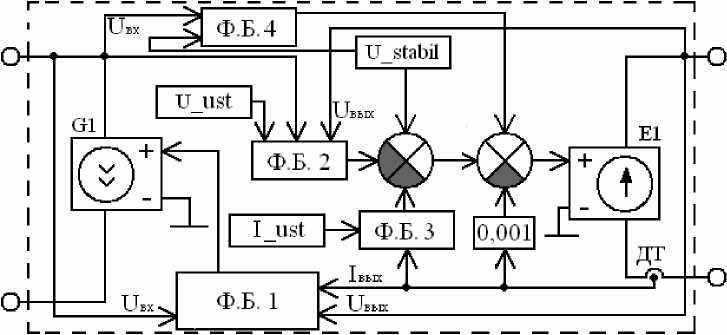
Рис. 1. Структурная схема энергетической модели импульсного стабилизатора напряжения

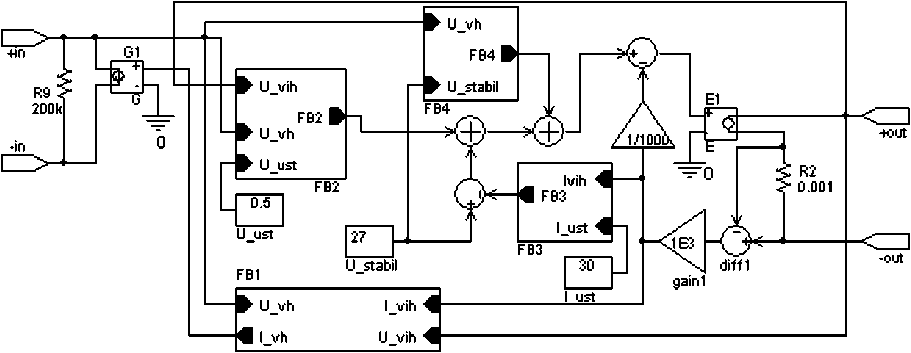
Рис. 2. Модель ИСН, созданная в пакете OrCAD 9.2 с использованием функциональных блоков

Функциональный блок ФБ1 используется для расчета коэффициента полезного действия и выходного тока модели ИСН. Значение КПД задается в виде функции η = f ( U вых , U вх , P нагр ). Величина P вх определяется по формуле P вх = P вых /η, после чего рассчитывается входной ток I вх = P вх / U вх . Таким образом, мощность, потребляемая нагрузкой P вых , равна мощности на входе ИСН (с учетом КПД).

Функциональный блок ФБ2 выполняет две функции:

– обеспечивает стабилизацию выходного напряжения в номинальных режимах работы;

– прерывает режим стабилизации при снижении входного напряжения ниже уровня напряжения стабилизации.

Если величина входного напряжения превышает значение U _stabil на величину больше значения, задаваемого блоком U _ust, то на выходе блока ФБ2 устанавливается значение 0, а на выходе модели ИСН – уровень, определяемый блоком U _stabil. В противном случае уровень сигнала на выходе блока ФБ2 возрастает, а выходное напряжение рассчитывается по формуле U вых = U вх – U _ust.

Функциональный блок ФБ3 предназначен для защиты по току. Если величина выходного тока не превышает величину, задаваемую блоком, то на выходе блока ФБ3 устанавливается 0. В противном случае уровень напряжения на выходе ФБ3 линейно увели- чивается, а уровень напряжения на выходе ИСН линейно уменьшается.

Источник напряжения, управляемый напряжением Е1 с коэффициентом передачи 1, обеспечивает требуемое значение напряжения на выходе ИСН. Датчик тока ДТ предназначен для определения тока I н в выходной цепи (нагрузка подключается к выходным клеммам модели). Мощность, потребляемая нагрузкой, рассчитывается по формуле P вых = U вых · I н . Ток нагрузки и, соответственно, мощность P _вых может меняться в зависимости от величины R н .

Функциональный блок ФБ4 предназначен для расчета астатической ошибки модели ИСН. В номинальном режиме работы величина астатической ошибки вычисляется по формуле ∆ = ( U вх – U _stabil)·0,001. При снижении входного напряжения до уровня напряжения стабилизации величина астатической ошибки становится равной нулю.

Модель понижающего стабилизатора напряжения, выполненная в пакете OrCAD с использованием функциональных блоков (рис. 2), состоит из входной и выходной цепей, блока FB1, рассчитывающего КПД модели, входной ток и входную мощность, блока FB2, стабилизирующего выходное напряжение в номинальном режиме работы, блока FB3, обеспечивающего защиту по току, и блока FB4, определяющего величину астатической ошибки.

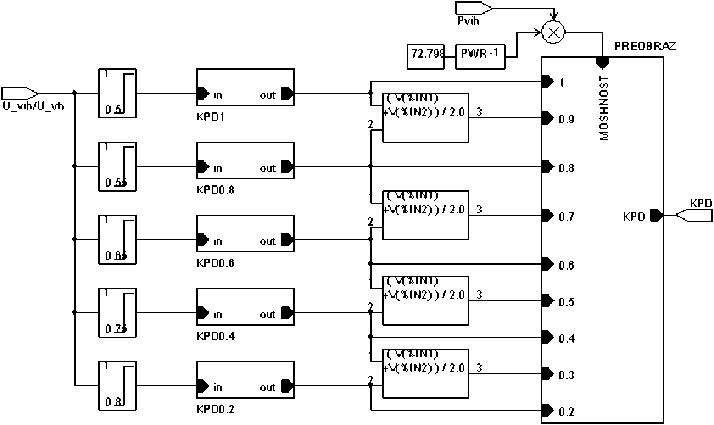
Рис. 3. Структурная схема функционального преобразователя КПД ИСН

Зависимость величины КПД от отношения U _вых / U _вх и мощности нагрузки

Диапазон P нагр	Соответствующее уравнение линии
0,95· P ном ≤ P нагр ≤ P ном	η(1) = –0,24·[( U вых – U вх ) –1]^2 + 0,96
0,85· P ном ≤ P нагр ≤ 0,95· P ном	η(0,9) = [η(1) + η(0,8)]/2
0,75· P ном ≤ P нагр ≤ 0,85· P ном	η(0,8) = –0,247·[( U вых – U вх ) –1]^2 + 0,92
0,25· P ном ≤ P нагр ≤ 0,35· P ном	η(0,3) = [η(0,4) + η(0,2)]/2
0,15· P ном ≤ P нагр ≤ 0,25· P ном	η(0,2) = –0,25·[( U вых – U вх ) –1]^2 + 0,79

Функциональный преобразователь КПД, входящий в состав блока FB1, предназначен для расчета величины КПД модели ИСН (рис. 3). Значение КПД задается в виде функции η = f ( U вых , U вх , P нагр ) (рис. 4).

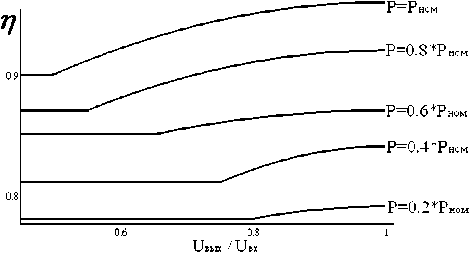
Рис. 4. Зависимость КПД от отношения U _вых /U_вх , для ряда мощностей нагрузки: P _ном = 72,798 Вт

Линии, приведенные на рис. 4, описываются следующими уравнениями:

η( P нагр = Р ном ) = –0,24·[( U вых – U вх ) – 1]^2 + 0,96,

η( P нагр = 0,8· Р ном ) = –0,247·[( U вых – U вх ) –1]^2 + 0,92,

η( P нагр

= 0,6· Р ном ) =

= –0,163 26·[( U вых – U вх ) –1]^2 + 0.87         (1)

η( P нагр = 0,4· Р ном ) = –0,48·[( U вых – U вх ) –1]^2 + 0,84, η( P нагр = 0,2· Р ном ) = –0,25·[( U вых – U вх ) –1]^2 + 0,79.

Введем промежуточные значения, которым соответствуют P _нагр = 0,9 · P _ном, P _нагр = 0,7 · P _ном, P _нагр = 0,5 · P _ном и P _нагр = 0,3 · P _ном. Уравнение для каждой из этих линий рассчитывается как среднее арифметическое между уравнениями двух линий, между которыми располагается данная линия, т. е. линия, соответствующая P нагр = 0,9 · P ном , определяется как [η( P _нагр = P _ном) + η( P _нагр = 0,8 · P _ном)]/2, и т. д.

Условия, на основании которых будут выводиться уравнения КПД в зависимости от мощности нагрузки, заданы в таблице. В ее первом столбце указаны диапазоны значений, в состав каждого из которых может входить величина, равная отношению P нагр / P ном . Во втором столбце приведены уравнения линий, соответствующие данным диапазонам.

Функциональный преобразователь КПД ИСН работает следующим образом. Блоки ABM и LIMIT задают уравнения (1). Иерархический блок PREOBRAZ предназначен для удовлетворения условий, представленных в таблице.

На вход блока PREOBRAZ поступают уравнения (1) и величина MOSHNOST, равная отношению мощности, потребляемой нагрузкой, к номинальной мощности на нагрузке (72,798 Вт). Ключевую роль в схеме играют блоки TABLE (рис. 5). Если на вход блока TABLE подается величина, находящаяся в диапазоне [0,85; 0,95), то на его выходе устанавливается 1, в противном случае – 0.

В блоке PREOBRAZ каждое уравнение, поступающее на его вход, умножается на величину, которая устанавливается на выходе соотнесенного с ним блока TABLE: в зависимости от величины P нагр / P ном на выходе только одного блока TABLE установится единица, на выходе всех остальных блоков – нули.

. TABLE____

In Out 0.849999V Dv 0.85v       1v

0.949999v 1v 0.95v       Ov

Рис. 5. Блок TABLE

После этого все результаты умножения суммируются и на выходе получается КПД, соответствующий одному отношению P нагр / P ном – тому, которое определяется условием в таблице.

Тестирование модели функционального преобразователя КПД ИСН. Предположим, что ( P _нагр / P _ном) = 0,91. Следовательно, рабочая точка должна двигаться по линии, соответствующей отношению ( P нагр / P ном ) = 0,9.

Проведем тестирование модели (рис. 6).

Линия, соответствующая отношению ( P нагр / P ном ) = 0,9, и линия, соответствующая выходу модели КПД, совпадают, отсюда можно сделать вывод, что модель составлена верно.

Тестирование модели ИСН. Тестирование модели ИСН проведено в трех режимах: режиме стабилизации выходного напряжения (рис. 7, а), режиме стабилизации выходного напряжения с демонстрацией режима снижения выходного напряжения при умень- шении входного напряжения (рис. 7, б) и режиме ограничения выходного тока (рис. 8, 9).

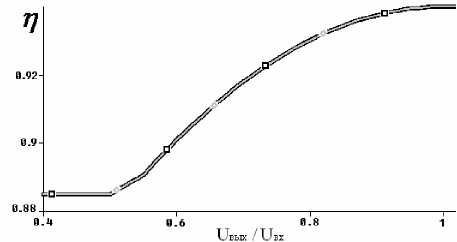
Рис. 6. Тестирование модели функционального преобразователя КПД ИСН

Анализ временных диаграмм (см. рис. 7) показывает, что если входное напряжение превышает уровень напряжения стабилизации, то на выходе модели будет стабильно поддерживаться напряжение, задаваемое блоком U _stabil. Если же уровень входного напряжения снизится до величины, близкой к уровню напряжения стабилизации, то выходное напряжение также начнет снижаться. Разница между выходным и входным напряжением задается блоком U _ust.

При тестировании модели ИСН в режиме тока ограничения (см. рис. 9) было определено, что коммутация нагрузки R 5 в момент времени t = 5 с приводит к росту тока нагрузки, но поскольку величина тока нагрузки не превышает уровня I _ust, то напряжение на выходе модели ИСН остается неизменным. Коммутация нагрузки R 6 в момент времени t = 15 с приводит к росту тока нагрузки, превышающему уровень I _ust, и напряжение на выходе модели ИСН снижается.

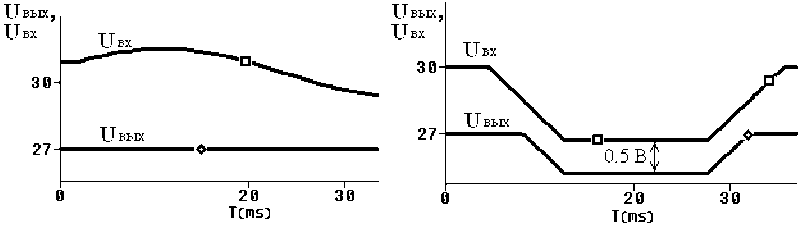
б

Рис. 7. Тестирование модели ИСН:

а – временная диаграмма режима стабилизации выходного напряжения; б – временная диаграмма режима стабилизации выходного напряжения с демонстрацией снижения выходного напряжения при уменьшении входного напряжения

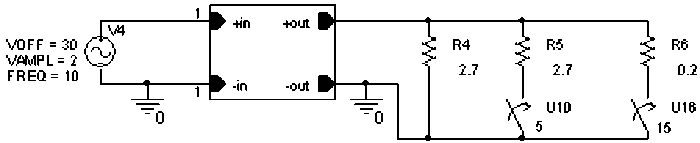
Рис. 8. Схема для тестирования модели ИСН в режиме тока ограничения

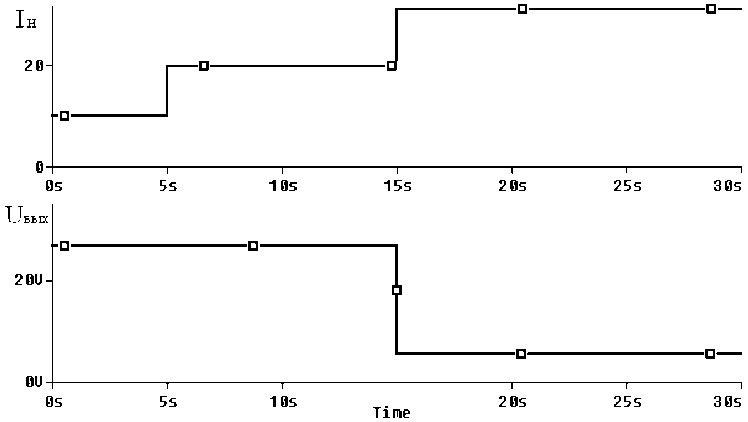
Рис. 9. Результаты тестирования модели ИСН в режиме тока ограничения

Таким образом, разработанная энергетическая модель импульсного стабилизатора напряжения с использованием функциональных блоков в программном пакете автоматизированного проектирования OrCAD обеспечивает возможность расчета энергетических характеристик в следующих режимах: режиме стабилизации выходного напряжения, режиме прерывания процесса стабилизации выходного напряжения при снижении входного напряжения ниже уровня напряжения стабилизации и режиме тока ограничения.

Использование представленной модели при проектировании энергетических режимов различных систем электропитания позволяет снизить длительность расчетов на 3…5 порядков без снижения их точности.