Разработка и исследование непараметрической оценки плотности вероятности, основанной на принципе декомпозиции обучающей выборки по ее объему

Непараметрические методы принятия решений, основанные на оценках плотности вероятности ядерного типа, широко применяются при исследовании объектов различной природы в условиях априорной неопределенности.

Вычислительная эффективность непараметрических алгоритмов во многом определяется объемом n статистических данных и снижается по мере его увеличения, что проявляется в росте временных затрат обработки информации. Возникающие проблемы затрудняют построение непараметрических систем принятия решений при анализе аэрокосмической информации, исследовании медико-биологических, экологических процессов и т. д., характеризующихся большими объемами априорной статистической информации.

Перспективным методом «обхода» возникающих проблем является применение принципов декомпозиции обучающих выборок по их объему и последовательных процедур принятия решений.

Цель данной работы – обосновать эффективность использования принципов декомпозиции при решении задач оценивания плотности вероятности в условиях больших выборок на основе анализа асимптотических свойств непараметрической оценки смеси плотностей вероятно- сти и результатов вычислительных экспериментов, а также разработать методику синтеза двухуровневой оценки плотности вероятности, обеспечивающей применение технологии параллельных вычислений.

Непараметрическая оценка смеси плотности вероятности и ее свойства . Пусть V = ( x¹ , i = 1, n ) - выборка из n независимых наблюдений одномерной случайной величины x с плотностью вероятности p ( x ) , вид которой априори неизвестен. Причем объем выборки достаточно большой, что снижает вычислительную эффективность непараметрических алгоритмов.

Разобьем исходную обучающую выборку V на K групп наблюдений Vj =( x1, i е Ij), j = 1, K . Здесь Ij – множество номеров наблюдений x, составляющих K j-ю группу, причем UI j = I = (i = 1, n).

j =1

На основе каждой выборки V_j построим непараметрическую оценку плотности вероятности [1]

ния c j ^ 0 , а n j c j ^ ” . Здесь и далее бесконечные пределы интегрирования опускаются.

Тогда при конечных значениях K непараметрическая оценка плотности вероятности p ( x ) обладает свойством асимптотической несмещенности и состоятельности.

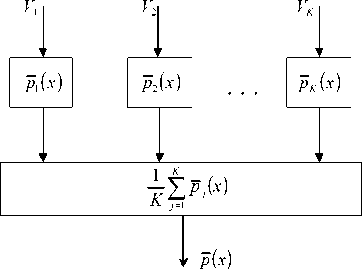
1-й уровень

2-й уровень

Рис. 1. Структура непараметрической системы оценки плотности вероятности, основанной на декомпозиции обучающей выборки по ее объему

p ^{( x} ) = Е^ф n j c j I j

(

x

c

xi ^

,

j = 1, K , (1) где Ф ( - ) — ядерные функции, удовлетворяющие условиям нормированности, положительности и симметричности; n j = [ i j ] - количество элементов множества I j ; c j = c ( n j ) - коэффициенты размытости ядерных функций, значения которых убывают с ростом n _j .

Оптимизацию оценок плотност ей вероятности по коэффициентам размытости c v , v = 1, к будем осуществлять в режиме «скользящего экзамена» из условия максимума функции правдоподобия

Доказательство

1. По определению

K

M (p(x ))=тЕ M (j x ))=

K j =1

1 K 1 ^f x - 11 =^Е-|ф —Ip(t) dt =

K j =1 c j ^ c j J

1 ^K

= —Е|ф(и) p(x-CjU) du,

^K j =1

где M – знак математического ожидания.

Разложим p ( x - c / и ) в ряд Тейлора и, ограничиваясь

где

L ( c ) = max

n

П p ( x

—            1      " f v ^j

p ^{( x}j ) = 7—ТгЕ Ф I^-

( n - 1) c i=1 (

- x1

c

.

В качестве приближения p ( x ) по статистической выборке V примем смесь непараметрических оценок плотностей вероятности

первыми двумя членами ряда, имеем p Р) (x) 1 K

W 1 = M ( p ( x ) ^- p ( x ) )---— — ^ c j- ,    (3)

² K j =1

где p ^{( 2 )} ( x ) - вторая производная плотности вероятности p ( x ) по x .

Отсюда при выполнении условий c j ^ 0 при n j ^ » следует свойство асимптотической несмещенности ста-

1 ^K

Р(x ) = tE Pj(x).

K j =1

тистики (2).

2. Рассмотрим выражение

Статистика типа (2) допускает использование технологии параллельных вычислений при оценивании плотности вероятности в условиях больших выборок.

Структура предлагаемой непараметрической системы оценки плотности вероятности представлена на рис. 1.

Асимптотические свойства p ( x ) определяются следующим утверждением.

Т еорема . Пусть p ( x ) и первые две ее производные ограничены и непрерывны; ядерные функции Ф ( и ) удовлетворяют условиям

Ф( и ) = Ф(- и), 0 <Ф( и )<«,

| ф ( и ) du = 1, | и ² Ф ( и ) du = 1, | и^т Ф ( и ) du <« , 0 < m <« ; последовательности c j = c j ( n j ) коэффициентов размытости ядерных функций таковы, что при n j ^ » , значе-

= Д-M

K ²

M |( p (x)- p (x ))2 dx =

K ₂

E |(p (x)- pj(x)) dx + j=1

KK

+E E|( p (x)- pj(x))(p (x)- pk (x))dx

. (4)

С учетом результатов исследования асимптотических

свойств традиционной непараметрической оценки Розен-

блатта–Парзена [2] вы раж ение (4) при достаточно больших значениях n j , j = 1, K принимает вид

M |( p (x) - p (x)) dx ~

= ^ M

K ²

f

K

E

ii ф(и )i г. jp(2)( x) Г L

njc

,E /E j c²

⁴         j =1 к =1

к * j

,

где ||Ф ( и )| |2 = | ф ² ( u ) du •

Нетрудно заметить, что при выполнении условий c j ^ 0 и n j c j ^ » при n j ^ » , j = 1, K оценка плотности вероятности (2) сходится к p ( x ) в среднеквадратическом, а с учетом свойств асимптотической несмещенности является состоятельной.

Сравнение аппроксимационных свойств непараметрической оценки (2) и традиционной оценки Розенблатта-Парзена p ( x ) . Для получения ана литич ески значимых результатов примем n j = n IK , j = 1, K . В это м слу чае можно полагать, что c = c ( n j ) = c ( n IK ) , j = 1, K .

На этой основе сравним отношения смещений, среднеквадратических отклонений и дисперсий непараметрических оценок p ( x ) и p ( x ) при оптимальных значениях коэффициентов размытости ядерных функций.

Асимптотическое выражение смещения для непараметрической оценки Розенблатта-Парзена p ( x ) имеет вид [2]

W2 = M ( p ( x )- p ( x )) ~ p 2( x) с2 ( n ) ’

Однако дисперсия оценки p ( x ) меньше, чем для традиционной статистики p ( x ) . В чем нетрудно убедиться, если сравнить дисперсионные составляющие

W =ЦфМ£ и W= 1ф«£

5 nc            nco в среднеквадратических отклонениях p (x) и p (x).

Их отношение

W6| W5 = c = K1/5 > 1. c-

Сравним вычислительную эффективность предложенной двухуровневой системы оценки плотности веро-

ятности и традиционного непараметрического алгоритма (1). Будем полагать, что объем частных выборок V j , j = 1, K одинаков и равен n I T , время расчета одной ядер-ной функции составляет т .

Тогда максимальное время, необходимое для приня-

а для оценки p ( x ) определяется выражением (3).

Вычислим отношение W, IW при оптимальных значениях коэффициентов размытости c - [ М и )1 Г '\ n lip(2)( x )||2

_ J K |ф( и )|² '⁵

_ ⁿ || p ^{<2)( x} )| f _

соответственно для оценок p ( x ) и p ( x ) .

После несложных преобразований получим

W 2 / W 1 = / <  1.

K т. е. смещение статистики p (x) больше по сравнению с p (x).

При разбиении исходной выборки V на K групп точек одинакового объема n I K выражение (5) при оптимальных коэффициентах c * преобразуется к виду

тия решения традиционным непараметрическим алгоритмом и предлагаемой системой, составляют значения

,        n т ( k + K )

L_n ® nk т , t ® —4-----у Вычислим их отношение:

тр           п        _K

— =-----. Если значение k > K (характерное для боль- tn   k + K ших выборок), то вычислительная эффективность предлагаемой системы возрастает по мере роста K.

Исследование свойств двухуровневой непараметрической оценки плотности вероятности . На основании данных вычислительного эксперимента сравнивались эффективность предлагаемого алгоритма (2) с хорошо зарекомендовавшим себя на практике традиционным непараметрическим алгоритмом (1) оценки плотности вероятности.

Традиционный алгорит м ст роился на полной обучающей выборке V = ( x i , i = 1, n ) .

Исследования осуществлялись при решении задачи оценки плотности вероятности, законы распределения формировались датчиками случайных чисел:

- для равномерного закона распределения x i = 10 ■ £ i , i = 1, n , при £ e [ 0;1 ] - случайная величина с равномерным законом распределения;

- для нормального закона распределения

W ₃ ~

11 ^{ф (} u )1 Г ₊ c ■ p ' x

Гг

nc

II Ф( и Я2)

______xi = Mx + о ( 2еi -1)х -2 ■ ln ((2£-1)2 +(2£ -1)2) (2£-1)2 +(2£-1)2

, i = 1, n ,

при математическом ожидании Mx = 0,5 и среднеквад

n

Заметим, что при K = 1 выражение (6) совпадает со среднеквадратическим отклонением W ₄ для традицион-

ратическом отклонении о = 1,2.

Вычислительный эксперимент при фиксированных

условиях исследований проводился пять раз, полученные

ной оценки Розенблатта-Парзена [2]:

Г _Г

W 4

---

5 [M u i

n

।2

-   Ip(2>( x)||

1 ^ 5

.

Рассмотрим отношение

5 К 1'5

W4' W = _; . K * 1, которое подтверждает несколько большую эффективность в среднеквадратическом непараметрической оценки p ( x ) по сравнению с предлагаемой p ( x ) .

результаты расчетов усреднялись.

Для определении эффективности предлагаемой оценки плотности вероятности использовался среднеквадратический критерий эффективности

1                                     х2

W = “Е( p^px ) - p.(x ) ) ,            (7)

n i = 1'

где n -объем выборки; p ( x ) - искомая плотность вероятности; p ( x ) - вычисленная оценка плотности вероятности.

Эффективность как традиционного (1), так и предлагаемого алгоритма (2) увеличивается с ростом объема обучающей выборки V (рис. 2, 3).

При этом отмечается некоторое ухудшение результатов оценки плотности вероятности при увеличении количества групп K обучающей выборки V (рис. 4).

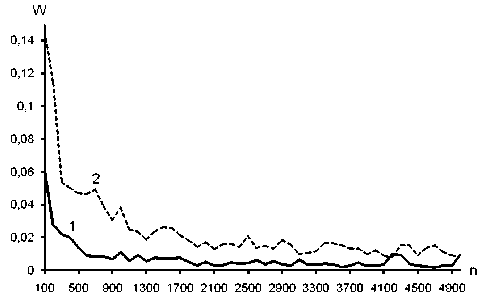
Рис. 2. Зависимость критерия эффективности (7) от объема выборки n . Кривые 1, 2 соответствуют традиционному методу и предлагаемому методу (1) при K ⁼ 4^.

Закон распределения – нормальный; ядерная функция – параболическая

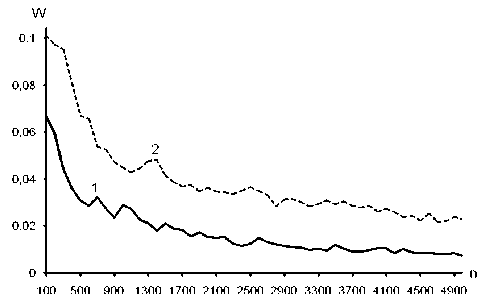
Рис. 3. Зависимость критерия эффективности (7) от объема выборки n . Кривые 1, 2 соответствуют традиционному методу и предлагаемому методу (1) при K = 4.

Закон распределения – равномерный; ядерная функция – параболическая

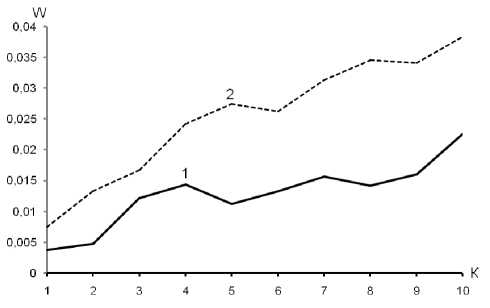
Рис. 4. Зависимость критерия эффективности (7) от количества групп K . Кривые 1, 2 соответствуют нормальному и равномерному законам распределения при объеме выборки n = 5 000.

Ядерная функция – параболическая

Результаты оценки времени выполнения алгоритмов приведены на рис. 5. Моделирование проводилось на компьютере с двухъядерным процессором Intel Core2Duo E6550 2.33GHz с разбиением вычислительного процесса на потоки (технология параллельных вычислений). Наблю- дается существенное сокращение времени расчетов при количестве групп K = 2. Дальнейшее сокращение времени расчетов при увеличении количества групп K происходит менее интенсивно. Для улучшения результатов рекомендуется использовать многопроцессорные системы.

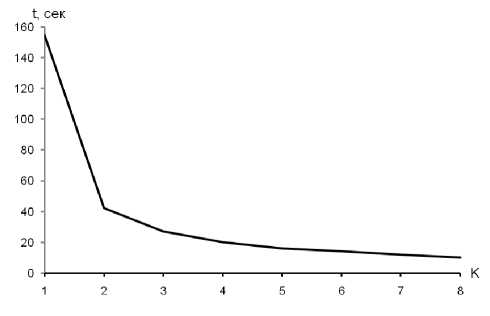
Рис. 5. Зависимость времени вычислений от количества групп K . Объем выборки n = 10000 .

Ядерная функция – параболическая

Вид используемой ядерной функции практически не оказывает влияния на эффективность оценки плотности вероятности (рис. 6).

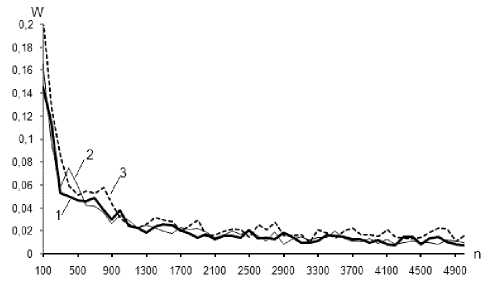
Рис. 6. Зависимость критерия эффективности от вида ядерной функции: кривые 1, 2, 3 соответствуют параболической, ступенчатой и треугольной ядерным функциям при объеме выборки n = 5 000 и K = 4

Таким образом, на основе анализа асимптотических свойств непараметрической оценки смеси плотностей вероятности обоснована возможность декомпозиции исходных статистических данных при синтезе непараметрических статистик в условиях больших выборок. С этих позиций предложена методика построения двухуровневой непараметрической системы оценки плотности вероятности, характеризующейся высокой вычислительной эффективностью. Приведены результаты вычислительных экспериментов, которые подтверждают правильность аналитических исследований.

Перспективность данного направления исследований состоит в возможности построения целого ряда модификаций многоуровневых непараметрических систем оценки плотности вероятности и использовании технологии параллельных вычислений.