Разработка и исследование параллельной модели алгоритмов пчелиных колоний для решения задач криптоанализа
Автор: Чернышев Юрий Олегови, Сергеев Александр Сергеевич, Рязанов Александр Николаевич, Дубров Евгений Олегович
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 1 (88) т.17, 2017 года.
Бесплатный доступ
Введение. Научное направление «природные вычисления» в последнее время широко используется для решения оптимизационных NP-полных задач, в том числе комбинаторных задач криптоанализа. В статье приводится краткий обзор публикаций, посвященных применению природных (биоинспирированных) методов для криптоанализа. Основной целью работы является исследование возможности применения алгоритмов пчелиных колоний для реализации криптоанализа блочных шифров. Материалы и методы. Для решения данной оптимизационной задачи применяются известные методы пчелиных колоний, относящиеся к сравнительно новому классу биоинспирированных оптимизационных методов, имитирующих процессы, протекающие в живой природе. Приводится описание и структурная схема алгоритма колонии пчел для решения задачи криптоанализа, отмечаются основные операции, выполняемые параллельно на глобальном уровне. Далее определяется множество независимых операторов, допускающих параллельное выполнение. С этой целью строятся информационно-логические граф-схемы алгоритма с введенными связями по управлению и по информации, а также формируются матрицы следования, логической несовместимости и независимости. По данной матрице независимости возможно определение множества операторов алгоритма, которые допускают параллельное выполнение. При этом размерность максимального внутренне устойчивого множества определяет максимальное число процессоров, используемых для реализации алгоритма. Результаты исследования. Основными результатами являются теоретические оценки временной сложности алгоритма пчелиных колоний. Кроме того, приводится решение задачи: для алгоритма криптоанализа на основе построенного информационно-логического графа и для заданного времени найти необходимое наименьшее число процессоров однородной вычислительной системы и план выполнения операторов на них. Приводится оценка необходимого минимального числа процессоров для реализации алгоритма криптоанализа, а также оценка общего Обсуждение и заключения. Основными результатами исследования являются: разработка алгоритма колонии пчел, используемого для решения задачи криптоанализа; описание его структурной схемы и основных параллельно выполняемых этапов; построение матрицы независимости; оценка числа процессоров для реализации алгоритма. Следует заметить (и это отмечалось в предыдущих работах), что отличительной особенностью применения биоинспирированных методов криптоанализа является возможность использования самого алгоритма шифрования (или расшифрования) в качестве целевой функции для оценки пригодности ключа, определенного с помощью операций биоинспирированного метода. Поэтому можно утверждать, что при использовании биоинспирированных методов процесс определения секретного ключа зависит не столько от сложности шифрующих преобразований, сколько от самого биоинспирированного метода, который должен обеспечивать достаточное разнообразие генерации ключей. времени реализации алгоритма
Криптоанализ, пчелиный алгоритм, пчелы-фуражиры, пчелы-разведчики, информационно-логический граф, матрица независимости
Короткий адрес: https://sciup.org/14250261
IDR: 14250261 | УДК: 004.056.55 | DOI: 10.23947/1992-5980-2017-17-1-144-159
Текст научной статьи Разработка и исследование параллельной модели алгоритмов пчелиных колоний для решения задач криптоанализа
Введение. Научное направление «природные вычисления» в последнее время широко используется для решения оптимизационных NP-полных задач, в том числе комбинаторных задач криптоанализа. В статье приводится краткий обзор публикаций, посвященных применению природных (биоинспириро-ванных) методов для криптоанализа. Основной целью работы является исследование возможности применения алгоритмов пчелиных колоний для реализации криптоанализа блочных шифров.
Материалы и методы. Для решения данной оптимизационной задачи применяются известные методы пчелиных колоний, относящиеся к сравнительно новому классу биоинспирирован-ных оптимизационных методов, имитирующих процессы, протекающие в живой природе. Приводится описание и структурная схема алгоритма колонии пчел для решения задачи криптоанализа, отмечаются основные операции, выполняемые параллельно на глобальном уровне. Далее определяется множество независимых операторов, допускающих параллельное выполнение. С этой целью строятся информационно-логические граф-схемы алгоритма с введенными связями по управлению и по информации, а также формируются матрицы следования, логической несовместимости и независимости. По данной матрице независимости возможно определение множества операторов алгоритма, которые допускают параллельное выполнение. При этом размерность максимального внутренне устойчивого множества определяет максимальное число процессоров, используемых для реализации алгоритма.
Результаты исследования. Основными результатами являются теоретические оценки временной сложности алгоритма пчелиных колоний. Кроме того, приводится решение задачи: для алгоритма криптоанализа на основе построенного информационно-логического графа и для заданного времени найти необходимое наименьшее число процессоров однородной вычислительной системы и план выполнения операторов на них. Приводится оценка необходимого минимального числа процессоров для реализации алгоритма криптоанализа, а также оценка
Introduction. The research area of “natural calculation” is now widely used for the solution to optimization NP-complete problems including combinatorial tasks of cryptanalysis. A quick overview of the publications devoted to the application of the natural (bioinspired) methods for cryptanalysis is provided. The main work objective is to investigate a possibility of applying bee colony algorithms to the realization of block cipher cryptanalysis.
Materials and Methods . The known bee colony techniques belonging to a relatively new class of the bioinspired optimization methods that simulate the processes occurring in wildlife are applied to solve this optimization problem. The description and the block diagram of the bee colony algorithm for the solution to a cryptanalysis task are provided; basic operations performed in parallel at the global level are noted. In the following, a set of independent operators allowing for the concurrent execution is defined. For this purpose, information-logical flowgraphs of the algorithm with the input control and information links are built, as well as matrices of succession, logical incompatibility, and independence are formed. This matrix of independence allows the definition of a set of algorithm operators admitting parallel execution. At that, the dimensionality of the maximal internally stable sets defines the maximum number of the processors used for the algorithm implementation.
Research Results. Theoretical estimates of time complexity of the bee colony algorithm are given as the key data. Besides, the problem solution is provided: to find the required smallest number of processors of the homogeneous parallel computing systems with distributed memory, and a uniform plan for the implementation of operators for them, for the cryptanalysis algorithm based on the constructed information-logical graph data-logical graph, and for the preset time. The assessment of the wanted smallest number of processors for the cryptanalysis algorithm implementation, and the общего
Обсуждение и заключения. Основными результатами исследования являются: разработка алгоритма колонии пчел, используемого для решения задачи криптоанализа; описание его структурной схемы и основных параллельно выполняемых этапов; построение матрицы независимости; оценка числа процессоров для реализации алгоритма. Следует заметить (и это отмечалось в предыдущих работах), что отличительной особенностью применения биоинспирированных методов криптоанализа является возможность использования самого алгоритма шифрования (или расшифрования) в качестве целевой функции для оценки пригодности ключа, определенного с помощью операций биоинспирированного метода. Поэтому можно утверждать, что при использовании биоинспирированных методов процесс определения секретного ключа зависит не столько от сложности шифрующих преобразований, сколько от самого биоинспи-рированного метода, который должен обеспечивать достаточное разнообразие генерации ключей.
времени реализации алгоритма evaluation of the total time of the algorithm realization are given.
Discussion and Conclusions . The basic research results are: the development of the bee colony algorithm used for the cryptanalysis task solution; the description of its flowchart and the principal parallel executed stages; the construction of a matrix of independence; the evaluation of the number of processors for the algorithm implementation. It should be noted (and it was observed in the previous works) that the distinctive feature of applying the bioinspired methods of cryptanalysis is the applicability of the encryption-decryption algorithm as a criterion function for the evaluation of the key acceptability defined by the bioinspired method operations. Thus, it can be affirmed that when using the bioinspired methods, the secret key definition process depends not so much on the complexity of the encryption transformations, as on the bioinspired method itself which should provide a sufficient diversity of the key generation.
граф, матрица независимости.
Введение. Научное направление «природные вычисления», объединяющее математические методы, в которых заложен принцип природных механизмов принятия решений, в последние годы получает все более широкое распространение при решении оптимизационных задач, в том числе задач криптоанализа. В данных методах и моделях основным определяющим элементом является построение начальной модели и правил, по которым она может изменяться (эволюционировать). В течение последних лет были предложены разнообразные схемы эволюционных вычислений: генетический алгоритм, генетическое программирование, эволюционные стратегии, эволюционное программирование, модели поведения роя пчел, стаи птиц и колонии муравьев, модели отжига или потока и другие конкурирующие эвристические алгоритмы. В [1] рассмотрены методы решения задачи криптоанализа, относящейся к переборным задачам с экспоненциальной временной сложностью, для традиционных симметричных криптосистем, использующих шифры перестановки и замены, а также для шифров гаммирования с использованием генетических алгоритмов. Среди последних разработок эвристических методов, используемых для решения задачи параметрической оптимизации технических объектов, можно отметить стохастический алгоритм, основанный на модели поведения роя светлячков, рассмотренный в [2]. B [3] описаны методы криптографических атак на симметричные и ассиметричные криптосистемы с использованием биоинспирированных методов (алгоритмов муравьиных и пчелиных колоний). В [4, 5] исследована возможность применения методов генетического поиска для реализации криптоанализа блочных криптосистем.
Данные задачи криптоанализа в большинстве случаев являются NP-полными и имеют комбинаторную сложность. В связи с этим, как отмечено в [6], основным мотивом для разработок новых алгоритмов решения комбинаторных задач являются возникшие потребности в решении задач большой размерности. В то же время, как отмечено в [7], недостатком методов эволюционной адаптации и генетических алгоритмов является наличие «слепого» поиска, что в ряде случаев приводит к увеличению времени поиска, генерации большого количества одинаковых и плохо приспособленных решений и увеличивает вероятность попадания в локальный оптимум. В этом плане представляет интерес применение эвристических методов, инспирированных природными системами, в которых осуществляется поэтапное построение решения задачи (то есть добавление нового оптимального частичного решения к уже построенному частичному оптимальному решению). Одной из последних разработок в области роевого интеллекта является алгоритм пчел, который довольно успешно используется для нахождения экстремумов сложных многомерных функций [8, 9]. Отметим, что в [8] приводится обзор некоторых публикаций, посвященных применению алгоритмов пчелиных колоний для решения комбинаторных теоретико-графовых задач (задача разбиения графа, раскраска графа, сравнение с другими биоинспирированными методами), решению задачи размещения, задачи разложения составных чисел на простые сомножители, используемoй при криптоанализе асимметричных алгоритмов.
Материалы и методы. В данной работе исследуется возможность параллельной реализации алгоритма пчелиных колоний, применение которого для реализации методов криптоанализа (симметричных и асимметричных криптосистем) описано ранее в [8–11]. При описании алгоритма криптоанализа воспользуемся методами и терминологией, используемыми в [6, 8]. Как отмечено в [6, 8], поведение пчелиного роя основано на самоорганизации, обеспечиваю- щей достижение общих целей роя при двухуровневой стратегии поиска. На первом уровне с помощью пчел-разведчиков формируется множество перспективных областей-источников. На втором уровне с помощью рабочих пчел-фуражиров исследуются окрестности данных областей. При этом основная цель колонии пчел — найти источник с максимальным количеством нектара.
Таким образом, итерационный процесс поиска решений при реализации алгоритма криптоанализа включает: — последовательное перемещение агентов-пчел на новые позиции в пространстве поиска;
-
— формирование соответствующих вариантов текста с последующей проверкой их оптимальности;
-
— выбор соответствующего оптимального (или квазиоптимального) варианта ключа [8].
В соответствии с [6, 8, 12] алгоритм колонии пчел включает следующие основные операции.
-
1. Формирование пространства поиска и создание популяции пчел.
-
2. Оценка целевой функции (ЦФ) пчел в популяции путем определения ЦФ, обусловливающей оптимальность исходного текста.
-
3. Формирование перспективных участков для поиска в их окрестности.
-
4. Отправка пчел-разведчиков и поиск агентами-разведчиками перспективных позиций для поиска в их окрестности.
-
5. Выбор пчел с лучшими значениями ЦФ с каждого участка.
-
6. Отправка рабочих пчел (пчел-фуражиров) для случайного поиска и оценка их ЦФ.
-
7. Формирование новой популяции пчел.
-
8. Проверка условия окончания работы алгоритма. Если они выполняются, переход к 9, иначе — к 2.
-
9. Конец работы алгоритма.
Структурная схема алгоритма колонии пчел приведена в [12]. Рассмотрим описание данного алгоритма для реализации криптоанализа [8, 9]. На первом этапе пчелиного алгоритма осуществляется формирование пространства поиска. Предположим, что каждая позиция a s пространства поиска представляет собой размещенный в пространстве символ алфавита текста. При этом каждая пчела-агент содержит в памяти упорядоченный список E s = { e s, , i = 1,2,^, n } посещенных символов. Этот список E s , поставленный в соответствие каждому символу, посещенному пчелой в пространстве поиска, фактически представляет решение — текст, для которого могут быть определены секретный ключ и ЦФ (например, с помощью функции Якобсена [1, 3, 8]).
Следующим этапом пчелиного алгоритма является формирование перспективных участков и поиск в их окрестности. Как и в [8], будем предполагать, что пространство поиска, в котором размещено m символов алфавита шифртекста, представляет собой квадратную матрицу А размером тхт . Для каждой позиции a s определена окрестность размера X для поиска, то есть множество позиций asi , находящихся на расстоянии (определяемом как количество элементов матрицы), не превышающем X, от позиции a s .
Применительно к решению задачи криптоанализа этапы данного алгоритма реализуются в следующей форме. Начальными параметрами алгоритма являются значение максимального размера окрестности для поиска Х макс и количество:
— пчел-агентов N ,
— итераций L ,
— агентов-разведчиков n , — агентов-фуражиров n y .
На l = 1 итерации алгоритма n r агентов-разведчиков случайным образом размещаются в пространстве поиска, то есть выбирается произвольным образом n r символов в матрице А . Значение ЦФ R на начальном этапе полагается равным малому положительному числу.
Далее в соответствии с [6, 12] выбирается n b лучших (базовых) решений, у которых значения ЦФ R не хуже, чем значения ЦФ у любого другого решения. На начальной итерации этот выбор может быть осуществлен случайным образом. В пространстве поиска формируется множество базовых позиций A b = { a bi }, соответствующих базовым решениям.
На следующем шаге алгоритма в окрестности каждой базовой позиции направляется заданное число рабочих пчел (фуражиров), имитирующих поиск нектара [8, 9].
После выбора агентом-фуражиром n y базовой позиции a i реализуется случайный выбор позиции a s , расположенной в окрестности X в границах 1 < X < Х макс базовой позиции a i .
Таким образом, каждой пчеле-агенту ставится в соответствие упорядоченный список E s посещенных символов пространства поиска с определенной для этого списка ЦФ. Данная последовательность ставится в соответствие последнему посещенному пчелой-агентом символу пространства поиска.
Аналогично [6, 8] вводится понятие области Di, представляющей собой Di = ai Y Oi, где Oi — множество позиций, выбранных агентами-фуражирами в окрестности позиции ai. В каждой области Di выбирается позиция а * с луч- шей оценкой ЦФ Ri * (оценка области Di). Среди всех оценок областей Ri * выбирается лучшая оценка Ri * и соответствующее решение (список Es). Вариант исходного текста с лучшим значением ЦФ запоминается, и осуществляется переход к следующей итерации.
На последующих итерациях алгоритма n r 1 агентов-разведчиков отправляются на поиск новых позиций ( n r i < П г ). Множество базовых позиций А ь (1) формируется из двух частей А ь 1 (1) и А ь 2 (1), при этом: — часть A b 1 (1) содержит n b 1 лучших решений а * , найденных в каждой из областей на итерации 1-1;
— часть A b 2 (1) содержит n b 2 лучших решений из n r 1 позиций, найденных пчелами-разведчиками на итерации 1 ( n b 1 + n b 2 = n b ).
Определяется число агентов-фуражиров, отправляемых в окрестности каждой базовой позиции. Каждым агентом-фуражиром n f выбирается базовая позиция a (1), а также позиция a s (1), расположенная в окрестности этой базовой позиции. Формируются области D i (1). В каждой области D i (1) выбирается лучшая позиция a i * c лучшей оценкой ЦФ R i * , и среди оценок R i * выбирается лучшая R * . Если R * (1) предпочтительней, чем R * (1-1), то соответствующее решение запоминается, и осуществляется переход к следующей итерации.
Таким образом, алгоритм криптоанализа на основе пчелиной колонии, приведенный в [8, 9], можно сформулировать следующим образом.
-
1. Определить начальные параметры алгоритма:
-
— количество пчел-агентов N ;
-
— количество итераций L ;
-
— количество агентов-разведчиков n r ;
-
— количество агентов-фуражиров n f ;
-
— значение максимального размера окрестности Х макс ;
-
— количество базовых позиций п ь ;
-
— nb 1 — количество базовых позиций, формируемых из лучших позиций а * , найденных на 1-1 итерации;
-
— n rl — количество агентов-разведчиков, выбирающих случайным образом новые позиции на итерациях 2,3,.., L ;
-
— n b 2 — количество базовых позиций, формируемых из n rl новых лучших позиций, найденных агентами-разведчиками на 1 итерации.
-
2. Задать номер итерации 1 = 1.
-
3. Разместить n r агентов-разведчиков случайным образом в пространстве поиска, то есть выбрать произвольным образом n r символов в матрице А . Положить значение ЦФ R равным малому положительному числу.
-
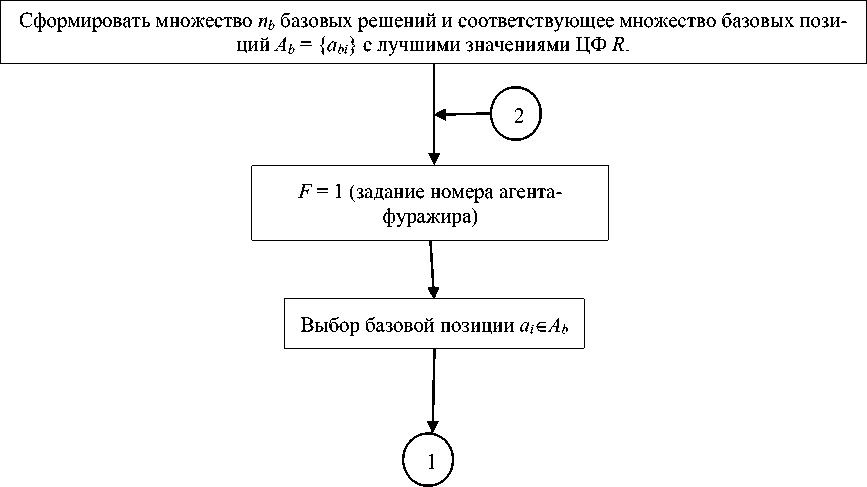
4. Сформировать множество n b базовых решений и соответствующее множество базовых позиций Аь = { a bi } с лучшими значениями ЦФ R .
-
5. Задание номера агента-фуражира f = 1.
-
6. Выбор базовой позиции a i е А ь .
-
7. Выбор позиции a s (1), расположенной в окрестности базовой позиции a i , не совпадающей с ранее выбранными на данной итерации позициями, и соответствующего решения (списка E s ).
-
8. Включить позицию a s в множество O i (где O i — множество позиций, выбранных агентами-фуражирами в окрестности позиции a i ).
-
9. Для всех вновь включенных позиций рассчитать и поставить им в соответствие решения E s и соответствующие значения ЦФ R .
-
10. f = f + 1, если f > n f , переход к п. 11, иначе — к п. 6.
-
11. Сформировать для каждой базовой позиции a i области D i = a i U O i .
-
12. В каждой области D i выбрать лучшую позицию a i * с лучшим значением ЦФ R i * .
-
13. Среди всех значений R i * выбрать лучшее значение R * и соответствующее решение (список позиций Е * ).
-
14. Если значение R * (1) предпочтительней значения R * (1-1), то сохранить значение R * (1), в противном случае сохраненным остается значение R * (1-1).
-
15. Если 1 < L (не все итерации пройдены), 1 = 1 + 1, переход к п. 16, иначе — к п. 20.
-
16. Начать формирование множества базовых позиций. Во множество Аь 1 включается n b 1 лучших позиций, найденных агентами среди позиций a i * в каждой из областей D i на итерации 1-1.
-
17. Разместить n rl агентов-разведчиков случайным образом в пространстве поиска для выбора n rl позиций в пространстве поиска.
-
18. Включить в множество Аь 2 n b 2 лучших позиций из множества n rl новых позиций, найденных агентами-разведчиками на итерации 1 ( n b 2 + n b 1 = n b ).
-
19. Определить множество базовых позиций на итерации 1 как Аь = Аь 1 U Аь 2 . Перейти к п. 5.
-
20. Конец работы алгоритма. Список Е * — вариант исходного текста с лучшим значением ЦФ R * .
Пример реализации данного алгоритма криптоанализа приведен в [4].
Структурная схема данного алгоритма представлена на рис. 1.
Определение начальных параметров алгоритма: количество пчел-агентов N ; количество итераций L ; количество агентов-разведчиков n r ; количество агентов-фуражиров n / ; значение максимального размера окрестности Х макс ; количество базовых позиций п ь ; п ь 1 — количество базовых позиций, формируемых из лучших позиций a * , найденных на 1-1 итерации; n rl — количество агентов-разведчиков, выбирающих случайным образом новые позиции на итерациях 2,3,.., L ; n b 2 — количество базовых позиций, формируемых из n rl новых лучших позиций, найденных агентами-разведчиками на 1 итерации.
Номер итерации 1 = 1
Размещение n r агентов-разведчиков случайным образом в пространстве поиска (выбор произвольным образом n r символов в матрице А ). Определить значение ЦФ R равным малому положительному числу.
Выбор позиции a s (l), расположенной в окрестности базовой позиции a i , не совпадающей с раннее выбранными на данной итерации позициями, и соответствующего решения (списка E s ).
Включение позиции a s в O i (множество позиций, выбранных агентами-фуражирами в окрестности позиции a i ).
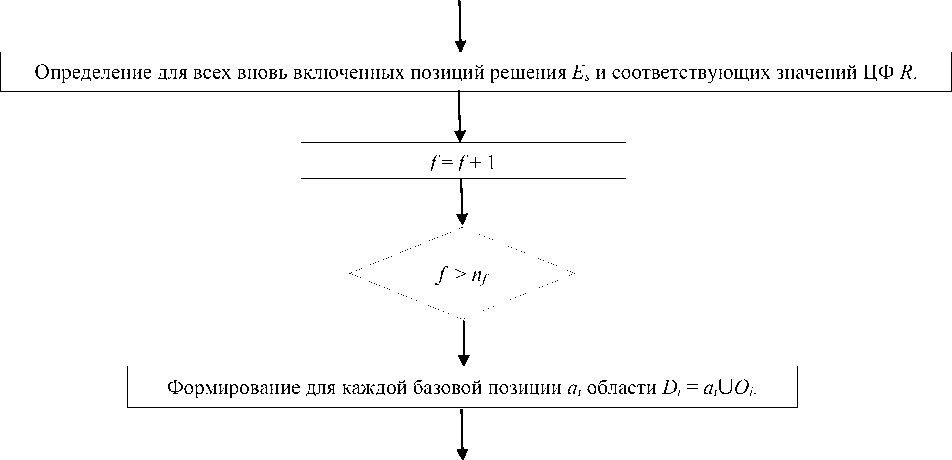
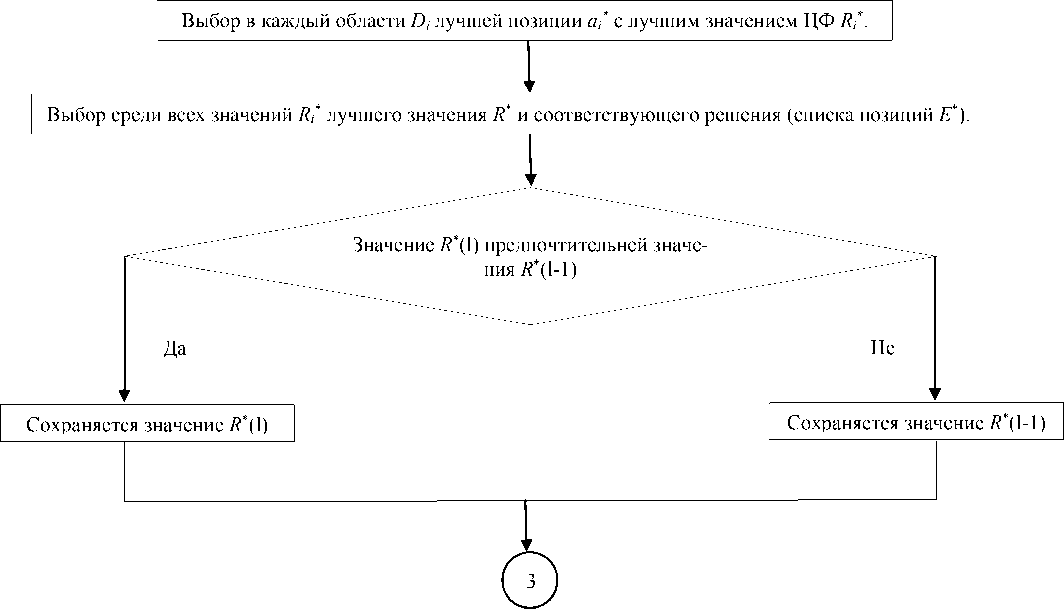
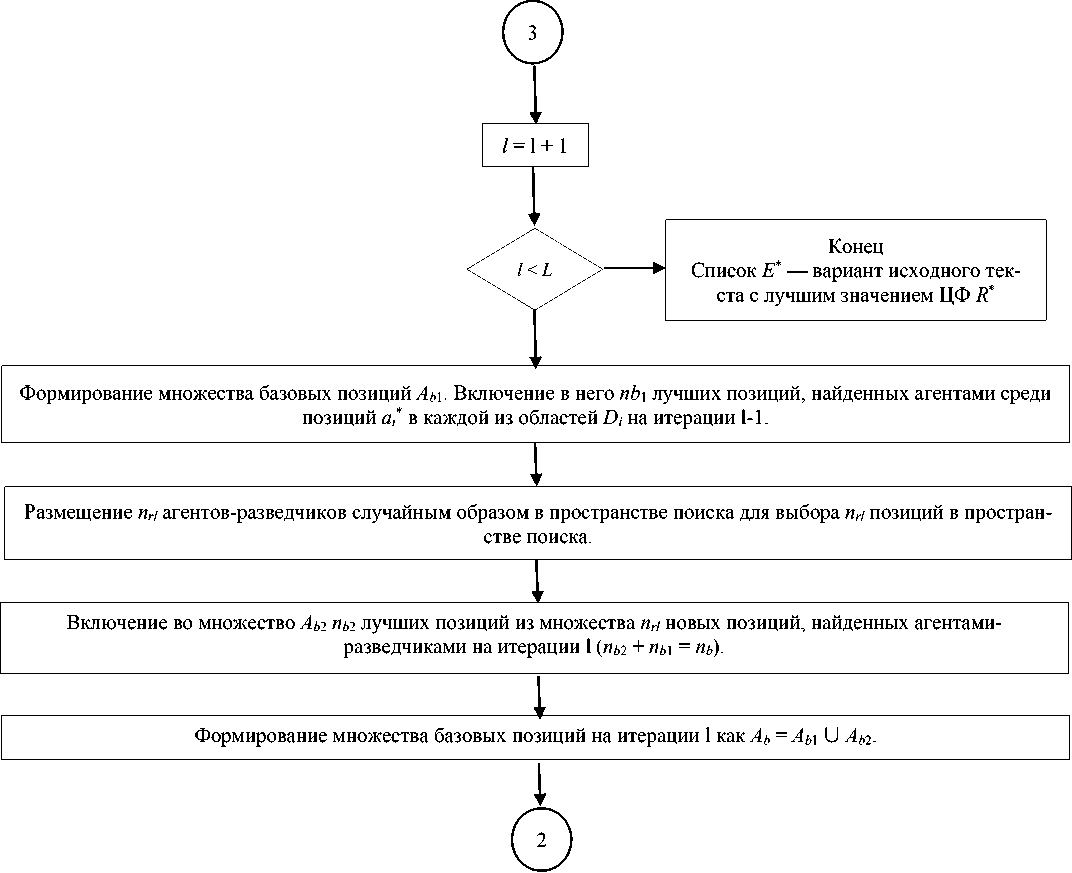
Рис. 1. Структурная схема криптоанализа на основе алгоритма колонии пчел
Fig. 1. Block scheme of cryptanalysis based on bee colony algorithm
Как и ранее в [4, 5], в соответствии с данной структурной схемой на глобальном уровне можно отметить следующие параллельно выполняемые этапы:
-
— параллельное размещение n r пчел-разведчиков случайным образом в пространстве поиска;
-
— параллельный выбор базовых позиций, позиций, расположенных в их окрестности, получение решений E s и соответствующих значений ЦФ R каждым агентом-фуражиром;
-
— параллельное формирование областей D i и выбор в них лучших позиций а i * с лучшим значением ЦФ R i * ;
-
— параллельное размещение n rl агентов-разведчиков в пространстве поиска для выбора n rl позиций.
Таким образом, с учетом данных преобразований структурную схему пчелиного алгоритма можно представить в виде, показанном на рис. 2. Для упрощения будем предполагать, что: — число агентов-разведчиков n r = 5;
-
— число базовых решений n b = 4;
-
— число агентов-фуражиров n f = 5;
-
— пы = 2 — количество базовых позиций, формируемых из лучших позиций а * , найденных на 1-1 итерации;
-
— п ь2 = 2 — количество базовых позиций, формируемых из пг / новых лучших позиций, найденных агентами-разведчиками на l итерации.
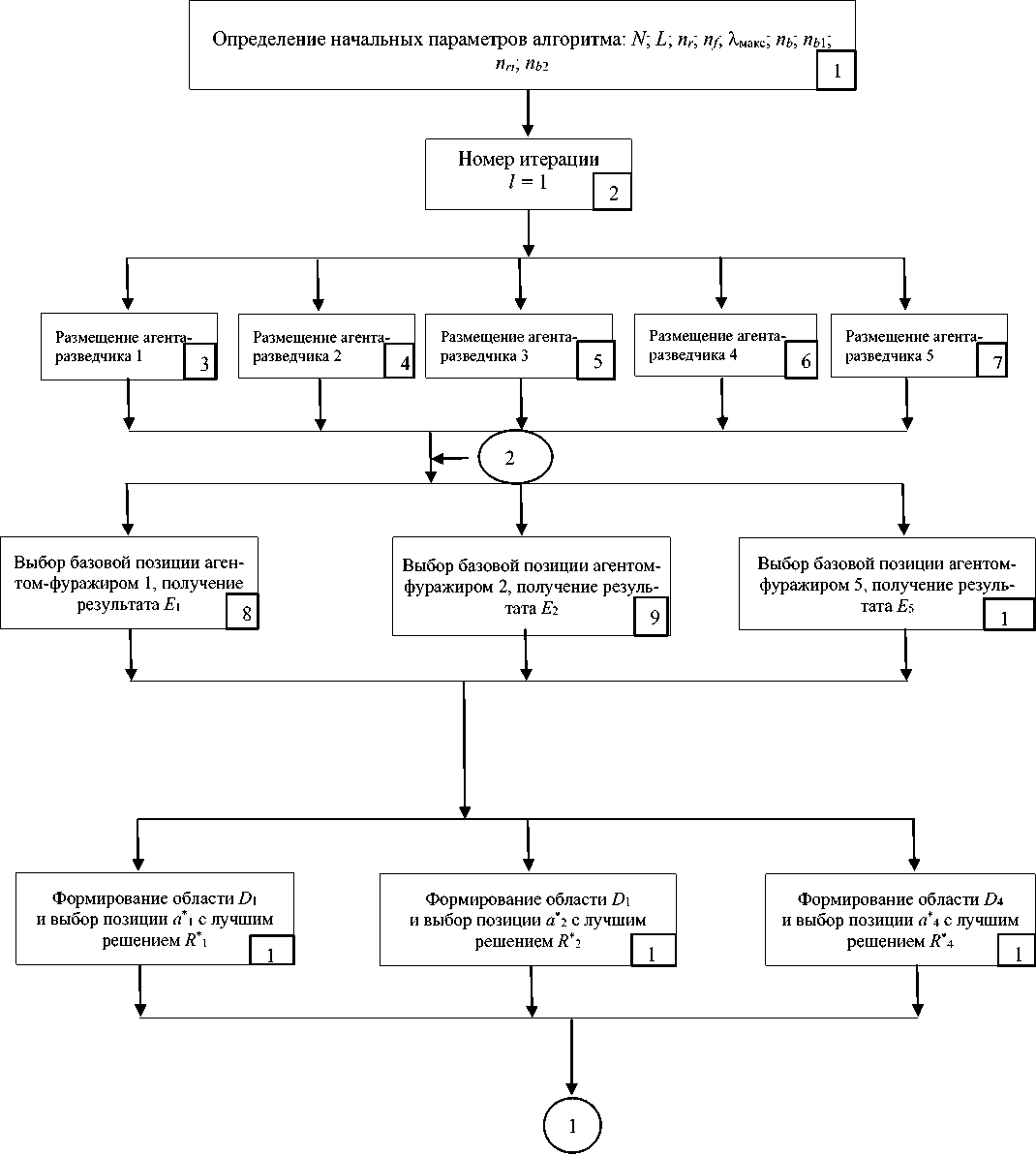
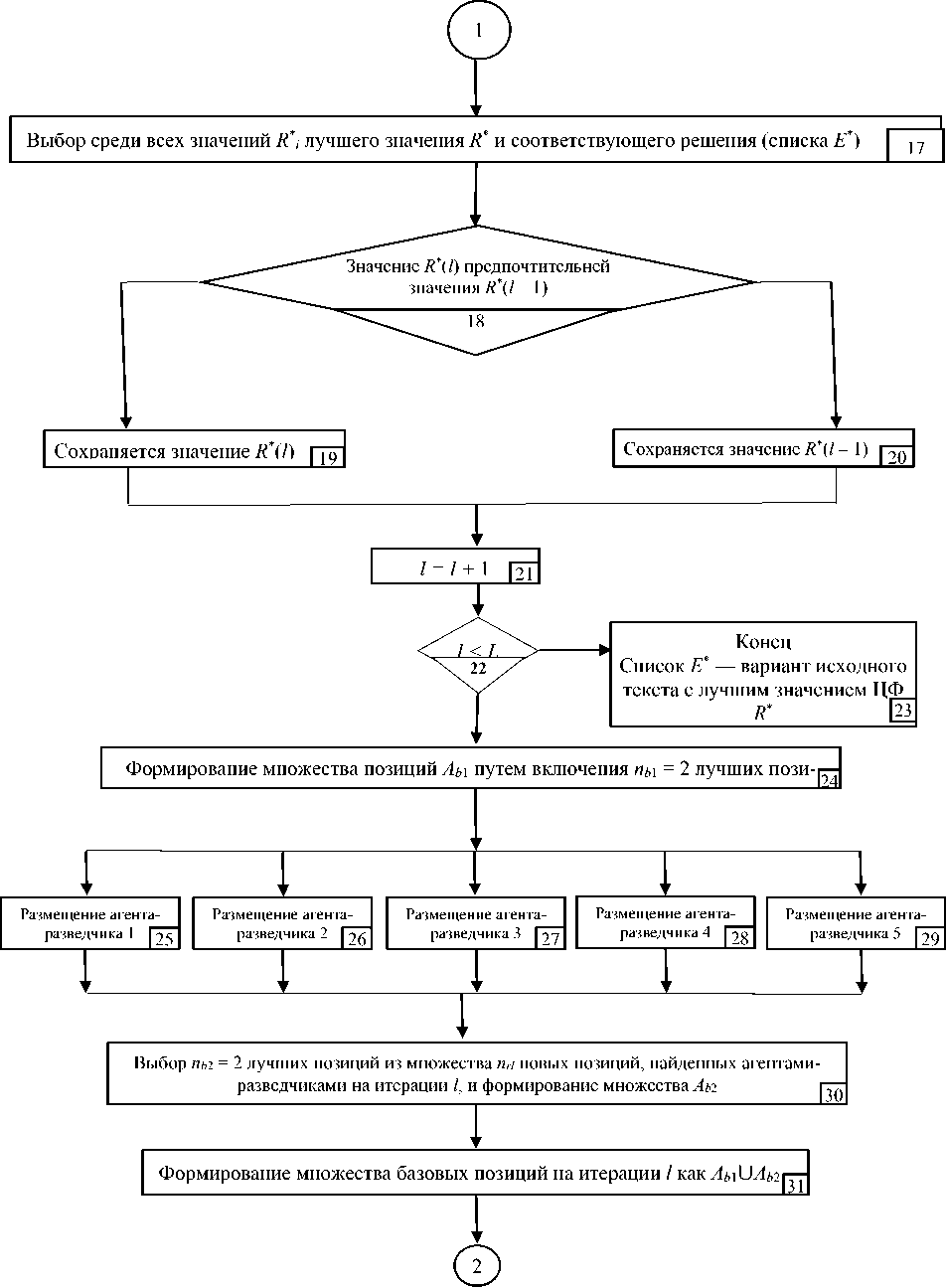
Рис. 2. Структурная схема криптоанализа на основе алгоритма пчел с учетом параллельно выполняемых этапов
Fig. 2. Block scheme of cryptanalysis based on bee colony algorithm with account of concurrent stages
Для дальнейшего определения множества независимых операторов, допускающих параллельное выполнение, будем, как и ранее в [4, 5], использовать методы, описанные в [13]. Для данной структурной схемы, показанной на рис. 2, составим информационно-логическую граф-схему G , отобразив в ней связи по управлению (двойная линия) и по информации (одинарная линия) (рис. 3). На рис. 3 двойной линией отмечены связи 18–19, 18–20 и 22–23, 22–24.
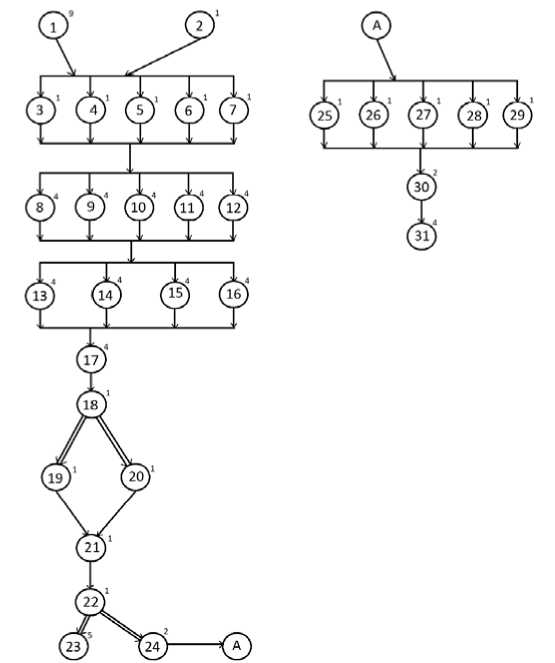
Рис. 3. Информационно-логическая граф-схема алгоритма криптоанализа
Fig. 3. Information-logical flowgraph of cryptanalysis algorithm
Для данного графа введем в рассмотрение матрицу следования S . В соответствии с [13] элемент S ij =*, если существует связь по управлению, и S ij = 1, если существует связь по информации (рис. 4).
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 0 |
1 1 |
1 2 |
1 3 |
1 4 |
1 5 |
1 6 |
1 7 |
1 8 |
1 9 |
2 0 |
2 1 |
2 2 |
2 3 |
2 4 |
2 5 |
2 6 |
2 7 |
2 8 |
2 9 |
3 0 |
3 1 |
|
|
1 |
|||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||
|
3 |
1 |
1 |
|||||||||||||||||||||||||||||
|
4 |
1 |
1 |
|||||||||||||||||||||||||||||
|
5 |
1 |
1 |
|||||||||||||||||||||||||||||
|
6 |
1 |
1 |
|||||||||||||||||||||||||||||
|
7 |
1 |
1 |
|||||||||||||||||||||||||||||
|
8 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
9 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
10 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
11 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
12 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
13 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
14 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
15 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
16 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
17 |
1 |
1 |
1 |
1 |
|||||||||||||||||||||||||||
|
18 |
1 |
||||||||||||||||||||||||||||||
|
19 |
* |
||||||||||||||||||||||||||||||
|
20 |
* |
||||||||||||||||||||||||||||||
|
21 |
1 |
1 |
|||||||||||||||||||||||||||||
|
22 |
1 |
||||||||||||||||||||||||||||||
|
23 |
* |
||||||||||||||||||||||||||||||
|
24 |
* |
||||||||||||||||||||||||||||||
|
25 |
1 |
||||||||||||||||||||||||||||||
|
26 |
1 |
||||||||||||||||||||||||||||||
|
27 |
1 |
||||||||||||||||||||||||||||||
|
28 |
1 |
||||||||||||||||||||||||||||||
|
29 |
1 |
||||||||||||||||||||||||||||||
|
30 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||
|
31 |
1 |
Рис. 4. Матрица следования алгоритма пчелиных колоний Fig. 4. Succession matrix of bee colony algorithm
Далее, используя алгоритмы, описанные в [13], дополним матрицу S транзитивными связями (рис. 5), обозна- чив все элементы Sij = 1.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 0 |
1 1 |
1 2 |
1 3 |
1 4 |
1 5 |
1 6 |
1 7 |
1 8 |
1 9 |
2 0 |
2 1 |
2 2 |
2 3 |
2 4 |
2 5 |
2 6 |
2 7 |
2 8 |
2 9 |
3 0 |
3 1 |
|
|
1 |
|||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||
|
3 |
1 |
1 |
|||||||||||||||||||||||||||||
|
4 |
1 |
1 |
|||||||||||||||||||||||||||||
|
5 |
1 |
1 |
|||||||||||||||||||||||||||||
|
6 |
1 |
1 |
|||||||||||||||||||||||||||||
|
7 |
1 |
1 |
|||||||||||||||||||||||||||||
|
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||
|
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||
|
10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||
|
11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||
|
12 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||
|
13 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||||||||
|
14 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||||||||
|
15 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||||||||
|
16 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||||||||
|
17 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||||
|
18 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||||||
|
19 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||
|
20 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||
|
21 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||
|
22 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
23 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||
|
24 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||
|
25 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||
|
26 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||
|
27 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||
|
28 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||
|
29 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||
|
30 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||
|
31 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Рис. 5. Матрица следования алгоритма пчелиных колоний, дополненная транзитивными связями
Fig. 5. Succession matrix of bee colony algorithm supplemented with transitive relations
Также сформируем симметричную матрицу следования S ` (рис. 6) и введем в рассмотрение матрицу L логической несовместимости операторов. Данная матрица L очевидным образом будет содержать следующие ненулевые элементы, соответствующие логически несовместимым операторам:
L (19,20) = L (20,19) = L (23,24) = L (23,25) =...= L (23,31) = L (24,23) = L (25,23) =…= L (31,23) = 1.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 0 |
1 1 |
1 2 |
1 3 |
1 4 |
1 5 |
1 6 |
1 7 |
1 8 |
1 9 |
2 0 |
2 1 |
2 2 |
2 3 |
2 4 |
2 5 |
2 6 |
2 7 |
2 8 |
2 9 |
3 0 |
3 1 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
6 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
12 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
13 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||
|
14 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||
|
15 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||
|
16 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||
|
17 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
18 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
19 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
20 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
21 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
22 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
23 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||
|
24 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
25 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||
|
26 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||
|
27 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||
|
28 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||
|
29 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||
|
30 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
31 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Рис. 6. Симметричная матрица следования алгоритма пчелиных колоний
-
Fig.6. Symmetric succession matrix of bee colony algorithm
Путем дизъюнктивного сложения этих матриц S ` и L получим матрицу независимости M , показанную на рис. 7.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 0 |
1 1 |
1 2 |
1 3 |
1 4 |
1 5 |
1 6 |
1 7 |
1 8 |
1 9 |
2 0 |
2 1 |
2 2 |
2 3 |
2 4 |
2 5 |
2 6 |
2 7 |
2 8 |
2 9 |
3 0 |
3 1 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
6 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
12 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
13 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||
|
14 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||
|
15 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||
|
16 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||
|
17 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
18 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
19 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
20 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
21 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
22 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
23 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
24 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
25 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
26 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
27 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
28 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
29 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||
|
30 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
31 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Рис. 7. Матрица независимости M алгоритма пчелиных колоний
-
Fig.7. Matrix of independence M of bee colony algorithm
Результаты исследования. Итак, по данной матрице независимости М можно очевидным образом определить множества операторов алгоритма, которые допускают параллельное выполнение. Размерность максимального внутренне устойчивого множества определяет максимальное число процессоров, используемых для реализации алгоритма.
Отметим, что теоретические оценки временной сложности алгоритма пчелиных колоний приведены в [12]. В лучшем случае временная сложность пчелиных алгоритмов Т составляет Т ≈ О (nlgn), в худшем случае Т ≈ О (n3). Как отмечено в [5], для повышения быстродействия и эффективности алгоритма за счет минимизации времени работы Т возможна организация процесса распараллеливания как на глобальном уровне (параллельная обработка Р элементов популяции на n процессорах), так и на локальном (параллельная реализация процесса оценки одного элемента попу- ляции). Таким образом, для повышения эффективности реализации алгоритма пчелиных колоний на локальном уровне в соответствии с [4] актуальной является задача: для алгоритма криптоанализа на основе построенного информационно-логического графа G и для заданного времени Тзад найти необходимое наименьшее число процессоров однородной вычислительной системы и план выполнения операторов на них.
Для решения этой задачи, как и ранее, воспользуемся методами, описанными в [13]. При этом в качестве времени Т зад примем, как и ранее, время Т кр — длину критического пути в информационно-логическом графе G . На первоначальном этапе при рассмотрении однородных вычислительных систем необходимо определение скалярных весов вершин в информационно-логическом графе, отражающих время выполнения операторов, составляющих схему на рис. 2.
Как и в [4, 5], для решения данной задачи воспользуемся методами, изложенными в [13]. Веса операторов, показывающие время их выполнения и определенные в соответствии с основными правилами анализа программ, описанными [14], приведены на рис. 3. Отметим, что данные веса определены в соответствии с отмеченными выше допущениями, что n r = 5; n b = 4; n f = 5; n b 1 = 2; n b 2 = 2, длина обрабатываемой строки текста (аналогично [8]) Т = 5. Легко убедиться, что критический путь в графе G Т кр = 35. В предположении, что Т зад = Т кр для представленного на рис. 3 информационно-логического графа и матрицы следования найдем ранние τ рi и поздние сроки τ п i окончания выполнения операторов с помощью алгоритмов, представленных в [13].
Ранние сроки:
τ р 1 = 9, τ р 2 = 1, τ р 3 = τ р 4 = τ р 5 = τ р 6 = τ р 7 = 10, τ р 8 = τ р 9 = τ р 10 = τ р 11 = τ р 12 = 14, τ р 13 = τ р 14 = τ р 15 = τ р 16 = 18, τ р 17 = 22, τ р 18 = 23, τ р 19 = τ р 20 = 24, τ р 21 = 25, τ р 22 = 26, τ р 23 = 31, τ р 24 = 28, τ р 25 = τ р 26 = τ р 27 = τ р 28 = τ р 29 = 29, τ р 30 = 31, τ р 31 = 35.
Поздние сроки:
τ п31 = 35 , τ п30 = 31 , τ п29 = τ п28 = τ п27 = τ п26 = τ п25 = 29 , τ п24 = 28 , τ п23 = 35 , τ п22 = 26 , τ п21 = 25 , τ п20 = τ п19 = 24 , τ п18 = 23 , τ п17 = 22 , τ п16 = τ п15 = τ п14 = τ п13 = 18 , τ п12 = τ п11 = τ п10 = τ п9 = τ п8 = 14 , τ п7 = τ п6 = τ п5 = τ п4 = τ п3 = 10 , τ п2 = τ п1 = 9.
В соответствии с методикой, описанной в [13], в матрице независимости найдем внутренне устойчивые множества, представляющие множества взаимно независимых операторов (ВНО). Это множества (1, 2), (3, 4, 5, 6, 7), (8, 9, 10, 11, 12), (13, 14, 15, 16), (25, 26, 27, 28, 29).
Используя значения τ рi и τ п i , как и ранее в [4, 5], оценим минимальное число процессоров для выполнения алгоритма за время Т кр . Для этого построим диаграммы ранних и поздних сроков окончания выполнения операторов и найдем такое распределение временных границ операторов для всех ВНО, при котором число используемых процессоров (функция n ) минимально [13]. Легко убедиться, что у операторов, входящих в данные множества ВНО, ранние и поздние сроки окончания выполнения равны, поэтому максимальное значение n = 5 имеет место для ВНО (3, 4, 5, 6, 7), ВНО (8, 9, 10, 11, 12), ВНО (25, 26, 27, 28, 29).
Таким образом, получена оценка числа процессоров n = 5, позволяющая выполнить алгоритм криптоанализа на основе метода пчелиных колоний за минимальное время Т = Т кр при отмеченных выше допущениях. Данная оценка является решением задачи, так как в соответствии с [13] в матрице независимости нет множеств ВНО, содержащих число операторов r > n .
Отсюда очевидным образом следует утверждение.
Утверждение . При реализации описанного выше параллельного алгоритма криптоанализа на основе метода пчелиных колоний, представленного информационно-логическим графом G на рис. 3 (в соответствии с технологией распараллеливания, описанной в [13]), необходимое минимальное число процессоров может быть определено как max( n r ; n f ; n b ). При этом общее время реализации алгоритма в общем случае составляет
Т = Q × T кр , где Q — количество итераций (в общем случае не превышающее длину блока текста), Т кр — длина критического пути в информационно-логическом графе G , определенная в соответствии с правилами анализа программ, описанными в [14].
Обсуждение и заключение. Таким образом, в данной работе:
-
— представлено описание алгоритма колонии пчел, используемого для реализации криптоанализа, его структурная схема;
-
— определены основные параллельно выполняемые этапы алгоритма, и на их основе построена информационнологическая граф-схема алгоритма;
-
— построены матрицы следования и независимости, позволяющие определить основные параллельно выполняемые операции алгоритма;
-
— приведена оценка числа процессоров, необходимых для реализации алгоритма.
В качестве заключения может быть представлен вывод, сделанный в публикациях [4, 5, 15, 16]. Основной отличительной особенностью применения биоинспирированных методов криптоанализа является возможность использования самого алгоритма шифрования (или расшифрования) в качестве целевой функции для оценки пригодности ключа, определенного с помощью генетических операций. Вследствие этого при использовании биоинспирированных методов криптоанализа процесс определения секретного ключа (например, при криптоанализе 2-го типа) зависит не столько от сложности шифрующих преобразований, сколько от самого биоинспирированного метода, который должен обеспечивать достаточное разнообразие генерации ключей. Это свидетельствует об актуальности задачи исследования возможности применения биоинспирированных алгоритмов для криптоанализа блочных криптосистем. Также следует заметить, поскольку отличительной особенностью как блочных методов шифрования, так и биоинспирированных методов (в частности, генетических алгоритмов), является их внутренний параллелизм [4], то задача разработки алгоритма криптоанализа на основе параллельной реализации составляющих этапов является актуальной.
Список литературы Разработка и исследование параллельной модели алгоритмов пчелиных колоний для решения задач криптоанализа
- Криптографические методы и генетические алгоритмы решения задач криптоанализа/Ю. О. Чернышев . -Краснодар: ФВАС, 2013. -138 с.
- Курейчик, В. В. Алгоритм параметрической оптимизации на основе модели поведения роя светлячков/В. В. Курейчик, Д. В. Заруба, Д. Ю. Запорожец//Известия ЮФУ. Технические науки. ¾ 2015. ¾ № 6 (167). ¾ С. 6-15.
- Биоинспирированные алгоритмы решения задач криптоанализа классических и асимметричных криптосистем/Ю. О. Чернышев . -Краснодар. высш. воен. училище им. ген. армии С. М. Штеменко, 2015. -132 с.
- Исследование возможности применения генетических алгоритмов для реализации криптоанализа блочных криптосистем/Ю. О. Чернышев //Вестник Дон. гос. техн. ун-та. -2015. -№ 3 (82). -С. 65-72.
- Исследование возможности применения методов эволюционной оптимизации для реализации криптоанализа блочных методов шифрования/Ю. О. Чернышев //Изв. СПбГЭТУ «ЛЭТИ». -2015. -№ 10. -С. 32-40.
- Лебедев, Б. К. Модели адаптивного поведения колонии пчел для решения задач на графах/Б. К. Лебедев, О. Б. Лебедев//Известия ЮФУ. Технические науки. ¾ 2012. ¾ № 7. ¾ С. 42-49.
- Лебедев, О. Б. Трассировка в канале методом муравьиной колонии/О. Б. Лебедев//Известия ЮФУ. Технические науки. ¾ 2009. ¾ № 4. ¾ С. 46-52.
- Исследование возможности применения бионических методов пчелиных колоний для реализации криптоанализа классических шифров перестановок/Ю. О. Чернышев //Вестник Дон. гос. техн. ун-та. -2014. -Т. 14, № 1 (76). -С. 62-75.
- Чернышев, Ю. О. Исследование и разработка методов криптоанализа шифров перестановок на основе биоинспирированных методов пчелиных колоний/Ю. О. Чернышев, А. С. Сергеев, Е. О. Дубров//Системный анализ в проектировании и управлении. Часть 1: сб. науч. тр. 17-й Междунар. науч.-практ. конф. -Санкт-Петербург: Изд-во Политехн. ун-та, 2013. -С. 143-150.
- Биоинспирированные методы криптоанализа асимметричных алгоритмов шифрования на основе факторизации составных чисел/А. С. Сергеев //Вестник Дон. гос. техн. ун-та. -2011. -Т. 11, № 9 (60). -С. 1544-1554.
- Чернышев, Ю. О. Применение биоинспирированных методов оптимизации для реализации криптоанализа классических симметричных и асимметричных криптосистем/Ю. О. Чернышев, А. С. Сергеев, Е. О. Дубров//Системный анализ в проектировании и управлении: сб. науч. тр. 16-й Междунар. науч.-практ. конф. -Санкт-Петербург: Изд-во Политехн. ун-та, 2012. -С. 112-122.
- Курейчик, В. В. Пчелиный алгоритм для решения оптимизационных задач с явно выраженной целевой функцией/В. В. Курейчик, М. А. Жиленков//Информатика, вычислительная техника и инженерное образование. -2015. -№ 1 (21). -С. 1-8.
- Сергеев, А. С. Параллельное программирование/А. С. Сергеев. -Ростов-на-Дону: Изд. центр ДГТУ, 2002. -77 с.
- Ахо, А.-В. Структуры данных и алгоритмы/А.-В. Ахо, Дж.-Е. Хопкрофт, Дж.-Д. Ульман. -Москва: Вильямс, 2003. -384 с.
- Применение биоинспирированных методов оптимизации для реализации криптоанализа блочных методов шифрования: монография/Ю. О. Чернышев . -Ростов-на-Дону: Изд-во ДГТУ, 2016. -177 с.
- Применение методов эволюционной оптимизации для реализации криптоанализа блочного метода шифрования AES/С. А. Капустин //Известия СПбГЭТУ «ЛЭТИ». -2016. -№ 8. -С. 25-40.
- Chernyshev, Y.O., et al. Kriptograficheskie metody i geneticheskie algoritmy resheniya zadach kriptoanaliza. Krasnodar: FVAS, 2013, 138 p..
- Kureichik, V.V., Zaruba, D.V., Zaporozhets, D.Y. Algoritm parametricheskoy optimizatsii na osnove modeli povedeniya roya svetlyachkov. Izvestiya SFedU. Engineering Sciences. 2015, no. 6 (167), pp. 6-15.
- Chernyshev, Y.O., et al. Bioinspirirovannye algoritmy resheniya zadach kriptoanaliza klassicheskikh i asimmetrichnykh kriptosistem. Krasnodar higher military school named after army general S. M. Shtemenko, 2015, 132 p..
- Chernyshev, Y.O., et al. Issledovanie vozmozhnosti primeneniya geneticheskikh algoritmov dlya realizatsii kriptoanaliza blochnykh kriptosistem. Vestnik of DSTU, 2015, no. 3 (82), pp. 65-72.
- Chernyshev, Y.O., et al. Issledovanie vozmozhnosti primeneniya metodov evolyutsionnoy optimizatsii dlya realizatsii kriptoanaliza blochnykh metodov shifrovaniya. Izvestiya SPbGETU "LETI", 2015, no. 10, pp. 32-40.
- Lebedev, B.K., Lebedev, O.B. Modeli adaptivnogo povedeniya kolonii pchel dlya resheniya zadach na grafakh. Izvestiya SFedU. Engineering Sciences. 2012, no. 7, pp. 42-49.
- Lebedev, O.B. Trassirovka v kanale metodom murav'inoy kolonii. Izvestiya SFedU. Engineering Sciences. 2009, no. 4, pp. 46-52.
- Chernyshev, Y.O., et al. Issledovanie vozmozhnosti primeneniya bionicheskikh metodov pchelinykh koloniy dlya realizatsii kriptoanaliza klassicheskikh shifrov perestanovok. Vestnik of DSTU, 2014, vol. 14, no. 1 (76), pp. 62-75.
- Chernyshev, Y.O., Sergeev, A.S., Dubrov, E.O. Issledovanie i razrabotka metodov kriptoanaliza shifrov perestanovok na osnove bioinspirirovannykh metodov pchelinykh koloniy. Sistemnyy analiz v proektirovanii i upravlenii. Chast' 1: sb. nauch. tr. 17-y Mezhdunar. nauch.-prakt. konf. St. Petersburg: Polytechnic University Publ. House, 2013, pp. 143-150.
- Sergeev, A.S., et al. Bioinspirirovannye metody kriptoanaliza asimmetrichnykh algoritmov shifrovaniya na osnove faktorizatsii sostavnykh chisel. Vestnik of DSTU, 2011, vol. 11, no. 9 (60), pp. 1544-1554.
- Chernyshev, Y.O., Sergeev, A.S., Dubrov, E.O. Primenenie bioinspirirovannykh metodov optimizatsii dlya realizatsii kriptoanaliza klassicheskikh simmetrichnykh i asimmetrichnykh kriptosistem. Sistemnyy analiz v proektirovanii i upravlenii: sb. nauch. tr. 16-y Mezhdunar. nauch.-prakt. konf. St. Petersburg: Polytechnic University Publ. House, 2012, pp. 112-122.
- Kureichik, V.V., Zhilenkov, M.A. Pchelinyy algoritm dlya resheniya optimizatsionnykh zadach s yavno vyrazhennoy tselevoy funktsiey. Informatika, vychislitel'naya tekhnika i inzhenernoe obrazovanie, 2015, no. 1 (21), pp. 1-8.
- Sergeev, A.S. Parallel'noe programmirovanie. Rostov-on-Don: DSTU Publ. Centre, 2002,77 p..
- Aho, A.V., Hopkroft, J.E., Ullman, J.D. Struktury dannykh i algoritmy. Moscow: Williams, 2003, 384 p..
- Chernyshev, Y.O., et al. Primenenie bioinspirirovannykh metodov optimizatsii dlya realizatsii kriptoanaliza blochnykh metodov shifrovaniya. Rostov-on-Don: DSTU Publ. Centre, 2016, 177 p..
- Kapustin, S.A., et al. Primenenie metodov evolyutsionnoy optimizatsii dlya realizatsii kriptoanaliza blochnogo metoda shifrovaniya AES. Izvestiya SPbGETU "LETI", 2016, no. 8, pp. 25-40.


