Разработка и исследование виброизоляторов с подстраиваемыми упругодемпфирующими характеристиками

рис. 1в показан предельный случай, когда длина прямолинейного участка а равна нулю. Получена формула нагрузочной характеристики данного вида виброизолятора в безразмерном виде:

2Я\   2 П

+ кХ + 4Х +—

• 3                   2 .              (1)

Построим график выражения (1) с целью определить влияние управляющего параметра а на жесткостные характеристики виброизолятора (см. рис. 2). При этом для безразмерной длины участка примем Х е [ 0;5 ] , для безразмерной деформации S y = ^[- ^1;2 ] , причем положительным будем считать перемещение, ведущее к сближению обойм виброизолятора. График на рис. 2а построен при использовании гипотезы о неизменной упругой линии в процессе деформации – классической гипотезы теории упругости [4], применимой в области малых деформаций, однако исследуемый объект является виброизолятором, т.е. работает при больших перемещениях, соизмеримых с размером упругого элемента. Поэтому, используя метод конечных элементов (МКЭ), определяется влияние на результат геометрической нелинейности в процессе деформации. Согласно рекомендациям [3], для расчета МКЭ использованы элементы балочного типа BEAM189; точность построения сетки конечных элементов – один конечный элемент на градус дуги окружности.

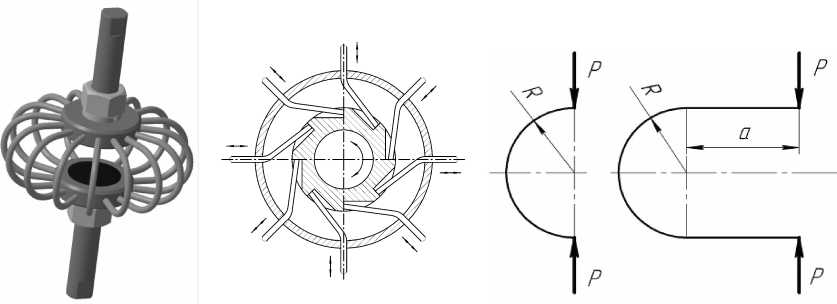
а)                             б)                            в)                   г)

Рис. 1. Виброизолятор с управляемыми жескостными характеристиками:

а) внешний вид; б) вариант управления длиной УДЭ; в) схема упругого элемента без прямолинейного участка; г) схема упругого элемента с прямолинейным участком

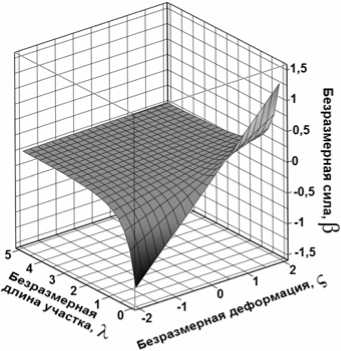
а)

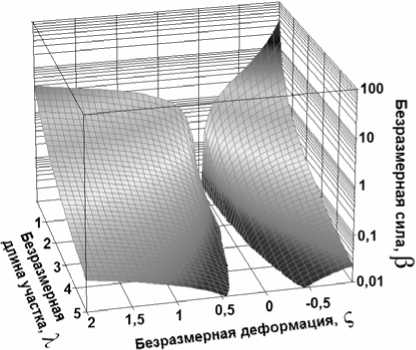
б)

Рис. 2. Графики зависимости безразмерной силы β от безразмерной деформации ςу и безразмерной длины участка λ: а) без учета геометрической нелинейности, б) с учетом геометрической нелинейности

Данный график можно аппроксимировать следующей функцией в=

^k 1 + ^k 2 ? y + ^k 3 ? ² + ^k 4 ? ³ + ^k 5 ^Л + ^k 6 ^²

тора в значительных пределах. Так, в диапазоне Ле ^{[ 0;}5 ^] безразмерная жесткость изменяется

10,8 раз, добившись эффективности виброизоляции Е [2] виброзащищаемого объекта на уровне 99,2%.

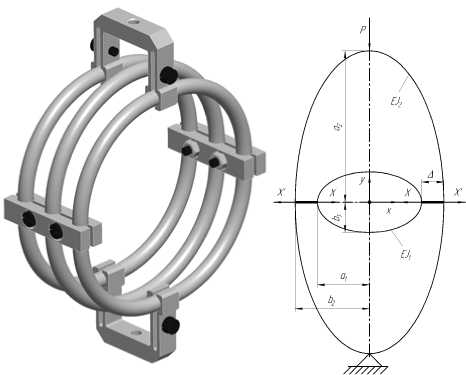
а)                        б)

Рис. 3. Двухэллипсный виброизолятор: а) внешний вид, б) схема расчетная

Рассмотрим случай, когда виброизолятор, состоящий из двух колец стянут абсолютно жесткими стяжками длинной Δ. В этом случае кольца деформируются и становятся эллипсами, как показано на рис. 3б, причем соотношение полуосей эллипсов зависит от величины Δ. Необходимо определить нагрузочную характеристику этой системы в нелинейной постановке. Обозначим параметры упругих элементов: R1 – радиус внутреннего кольца до стяжки; R2 – радиус внешнего кольца до стяжки; a1 – большая полуось внутреннего эллипса; b1 – малая полуось внутреннего эллипса; a2 – большая полуось внешнего эллипса; b2 – малая полуось внешнего эллипса; J1 – момент инерции поперечного сечения внутреннего эллипса; J2 – момент инерции поперечного сечения внешнего эллипса; E – модуль упругости материала. Используя математическое программное обеспечение, данные легко аппроксимируются функциональными выражениями в нужной пользователю области и с требуемой точностью. Для примера рассмотрим график на рис. 4, который может быть аппроксимирован одним выражением во всей исследованной области:

в _ k 1 + k 2 ln ц + k 3 In / + к 4 ln² ц + k ₅ ln² у + k 6 In ц- In у 1 + k 7 In ц + k 8 In у + k 9 ln² ц + k ₁₀ ln² у + k _n In ц - In у

,                                                (3)

Величина достоверности аппроксимации данного выражения R2=99,994%.

а)

б)

в)

д)

г)

е)

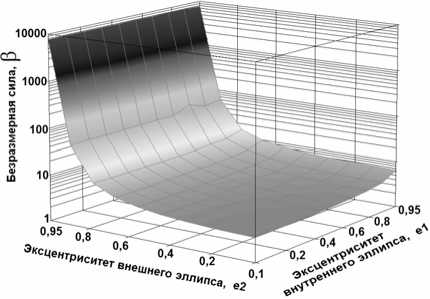
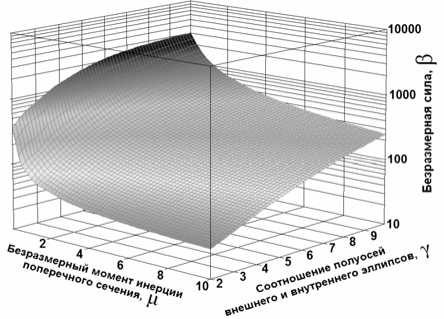
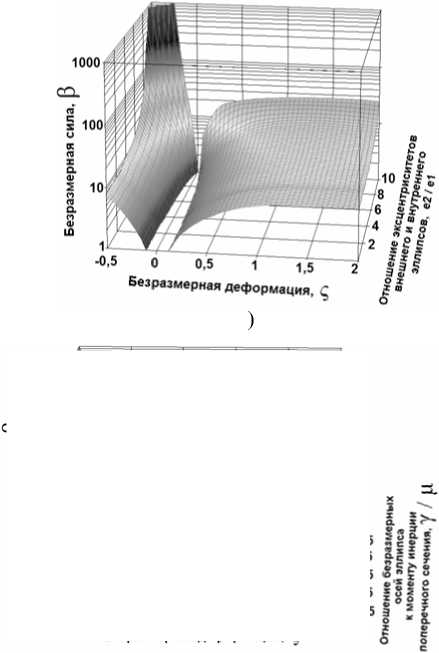
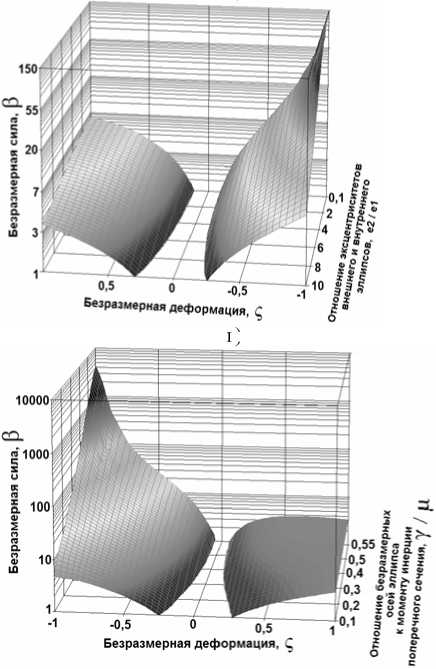
Рис. 4. График зависимости безразмерной силы β от безразмерных критериев:

а) от эксцентриситетов внешнего e2 и внутреннего e1 эллипсов для P||a при безразмерной деформации ςу= – 0,28; б) от безразмерного момента инерции поперечного сечения μ и соотношения полуосей внешнего и внутреннего эллипсов γ для P||a при безразмерной деформации ςу= – 0,28; в) от соотношения эксцентриситетов внешнего и внутреннего эллипсов е2/e1 и безразмерной деформации ςy для P||a; г) от соотношения эксцентриситетов внешнего и внутреннего эллипсов е2/e1 и безразмерной деформации ςy для P||b; д) от соотношения безразмерных полуоси эллипса и момента инерции поперечного сечения γ/μ и безразмерной деформации ςy для P||a; е) от соотношения безразмерных полуоси эллипса и момента инерции поперечного сечения γ/μ и безразмерной деформации ςy для P||b

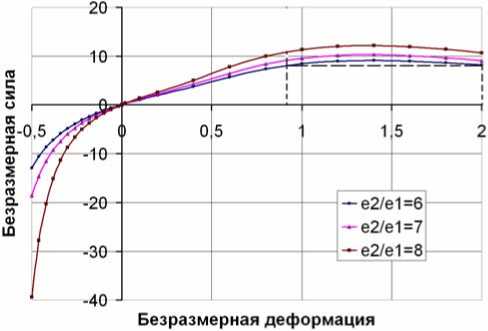
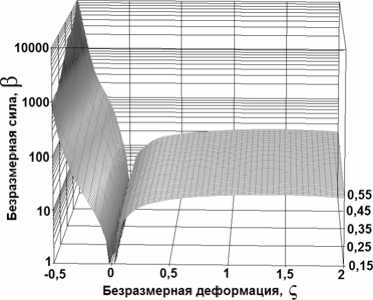
Рис. 5. График зависимости β = f(е2/e1, ςy) с областью, где жесткость близка к квазинулевой

Из анализа графиков, приведенных на рис. 4, 5 можно сделать вывод о большом диапазоне изменения характеристик двухкольцевого виброизолятора. Так, изменяя только параметр эллипсности колец, можно добиться изменения жесткости почти в 1000 раз, а изменение соотношения γ/μ в диапазоне от 0,15 до 0,55 позволяет изменять жесткость почти в 300 раз, и все это без существенного изменения габаритов виброизолятора, что позволяет добиться эффективности виброизоляции Е [2], близкой к 100%. Данная особенность делает рассматриваемый виброизолятор весьма интересным объектом, для создания на его базе управляемых виброзащитных систем. Построим график зависимости (см. рис. 5) безразмерных нагрузочных характеристик системы от безразмерной длины стяжки β=f(ς,ξ). Предполагается, что в начальный момент эллипсные при работе кольца, являются радиусными. Рассмотрим случай, когда начальные кольца имеют равные жесткости (μ=8). Из графика на рис. 6 видно, что изменением длины стяжки можно изменять жесткость виброизолятора в области сжатия в 5 раз, в области растяжения в 370 раз, что составляет примерно треть от теоретических возможностей виброизолятора, рассмотренных выше, но, тем не менее, является хорошим результатом на фоне других конструкций.

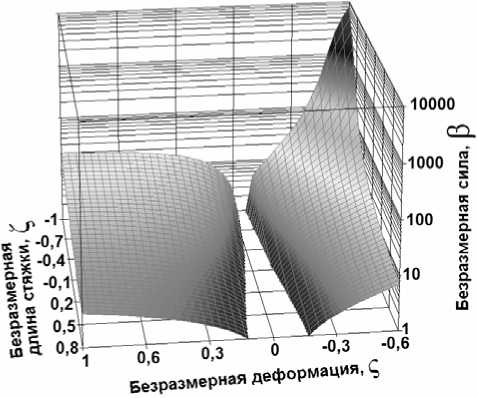
Рис. 6. График зависимости безразмерной силы β от безразмерной деформации ς и безразмерной длины стяжки ξ для μ=8

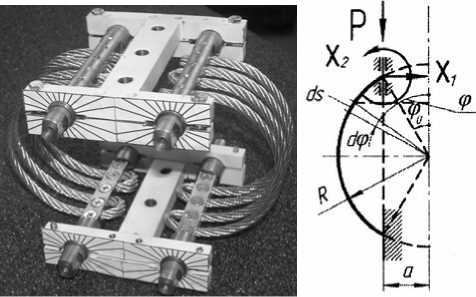
Рассмотрим виброизолятор, показанный на рис. 7 Виброизолятор представляет собой две разъемные обоймы, между обоймами которых осуществляется защемление возвратных петель тросового элемента, выполненного в виде непрерывного пространственного змеевика. Докажем, что изменением формы упругой линии и углом охвата упругого элемента кольцевого виброизолятора можно достаточно просто и в широких пределах регулировать его жескостные характеристики.

а)                       б)

Рис. 7. Виброизолятор с изменяемыми формами УДЭ: а) внешний вид, б) расчетная схема

На рис. 7б показана расчетная схема УДЭ исследуемого виброизолятора, представляющая собой сегмент окружности с закрепленными концами. Верхний конец, к которому приложена внешняя сила Р, имеет возможность перемещения в вертикальном направлении. Для наглядности полученные значения коэффициентов демпфирования γ ср сравниваются с предельными для материала МР и гофрированных пластинчатых виброизоляторов (см. рис. 8). Поскольку никаких специальных мер для увеличения демпфирования предпринято не было, средний коэффициент демпфирования γ ср исследуемого виброизолятора уступает им, но, тем не менее, оказывается вполне достаточным для обеспечения коэффициента динамичности η на резонансе менее трех.

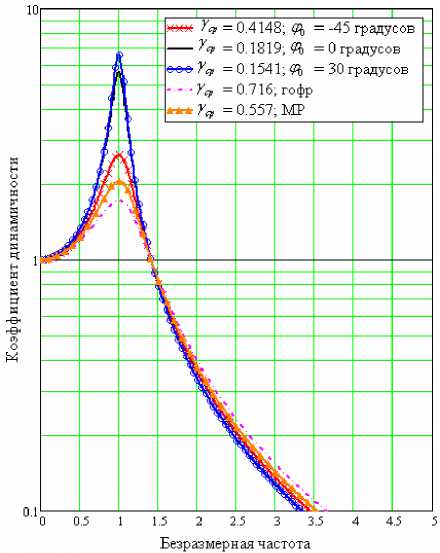
Рис. 8. График амплитудно частотной характеристики

Установлено, что коэффициент демпфирования изменяется вследствие двух противоположных тенденций:

• а)    площадь петли возрастает с уменьшением начального угла φ 0 , а вслед за ней растет и коэффициент демпфирования γ ср ;

• б)    с уменьшением начального угла φ 0 падает жесткость виброизолятора, что снижает значение коэффициента демпфирования γ ср . Именно поэтому при больших положительных углах φ 0 коэффициент демпфирования γ ср несколько возрастает, создавая минимум при значении начального угла защемления φ 0 =30º.

Итак, исследуемый виброизолятор имеет приемлемые демпфирующие характеристики, относительно прост конструктивно, может изменять за счет управления в процессе колебаний величиной начального угла φ 0 , свои жест-костные характеристики более чем в 20 раз, а демпфирующие почти в 3 раза, и таким образом демонстрирует преимущества управляемых виброизоляторов, основанных исключительно на конструкционном демпфировании.

Помимо управления жесткостью виброизоляторов с целью обеспечения нормальной работы оборудования в зарезонансном режиме, существуют методы управления демпфированием, влияющего, прежде всего, на амплитуду колебаний системы на резонансе. Условно можно разделить данные методы на такие, которые обеспечивают изменение демпфирования с сохранением неизменной жесткости и с совместным изменением жесткости и демпфирования. В свою очередь, по способу изменения характеристик можно выделить такие конструкции, в которых эффект достигается за счет свойств и способов закрепления самого упругого элемента и таких, где используются специальные преобразующие механизмы. Рассмотрим демпфер, показанный на рис. 9. Данный демпфер рассматривался как один из вариантов элементов системы виброзащиты беговой дорожки для «Международной космической станции (МКС)» и в перспективе для программы «Марс-2020».

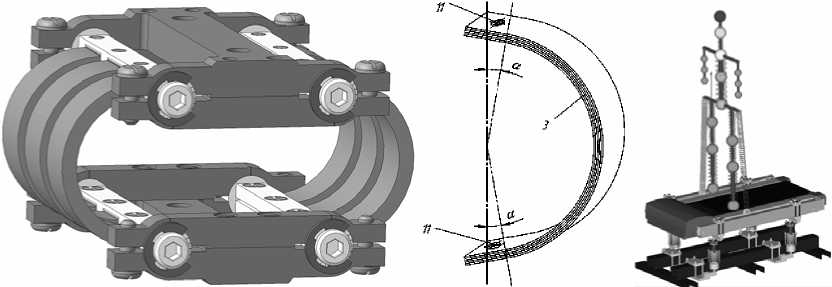
Рис. 9. Управляемый ленточный виброизолятор и вариант его применения:

а) внешний вид виброизолятора; б) УДЭ демпфера, где α – управляющий угол; 3 – пакет лент; 11 – крепежные отверстия; в) модель человека в условиях невесомости на беговой дорожке с исследуемыми демпферами

Построим нагрузочную характеристику демпфера в безразмерном виде, используя данные из работы [1]

I 4nI в = 1        I* Sy +1 am * Sy

Vn -8)       j=0         ,(4)

5l где Sy =. (5)

m

Рис. 10. График нагрузочной характеристики демпфера в безразмерном виде

Хотя количество лент и выше, чему у балочного виброизолятора с параболическим законом распределения коэффициента трения между слоями, в данном виброизоляторе поджатие слоев осуществляется за счет свойств самого упругого элемента, что делает рассматриваемый демпфер простым, надежным и компактным и позволяет получить огромный диапазон рассеяния энергии: от работы в режиме практически без трения – «чистая упругость», до режима, когда упругость демпфера пренебрежимо мала в сравнении с силой трения – «чистый демпфер», и все это без изменения его жесткостных и габаритных характеристик.

Рассмотрим конструкцию и работу виброизолятора, в котором управляющий параметр осуществляет одновременно изменение как жесткостных, так и демпфирующих свойств. Внешний вид такого виброизолятора приведен на рис. 11а. Предлагаемая конструкция виброизолятора подразумевает возможность регулирования жесткостных и демпфирующих характеристик путем торцевого поджатия внутреннего троса 4 с помощью резьбовых регулировочных пробок 16 их вращением по/против часовой стрелки на требуемый угол.

Точной зависимости толщины гистерезисной петли T0 от угла поворота пробки α пока не получено и включено в одно из направлений дальнейших научных исследований, однако, по аналогии с двумя представленными выше демпферами, можно ожидать достаточно высоких величин сил трения и предельного коэффициента рассеяния энергии ψ не ниже четырех. При этом радиус R и толщина гистерезисной петли T0 при регулировании изменяются в одном направлении. Данный виброизолятор прост конструктивно и технологически, дешев, имеет простую и проверенную модель расчета жесткостных свойств, при этом обеспечивает возможность совместного управления жесткостью и демпфированием.

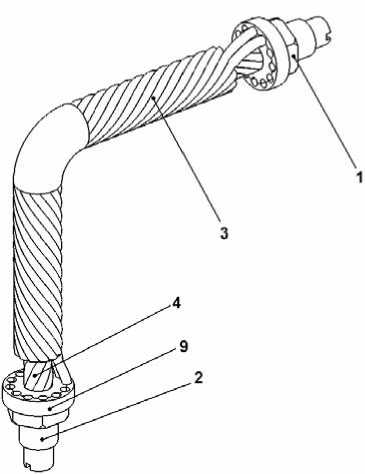
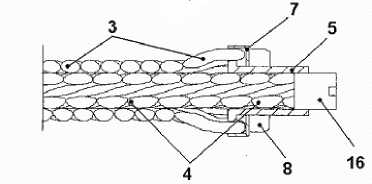
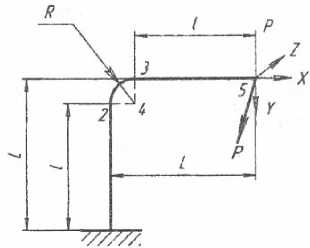
Рис. 11. Управляемый двуслойный тросовый Г-образный виброизолятор:

а) внешний вид; б) разрез УДЭ с обоймой; в) расчетная схема, где L – полная высота упругого элемента; l – длина прямолинейного участка; R – радиус скругления; P – внешняя сила

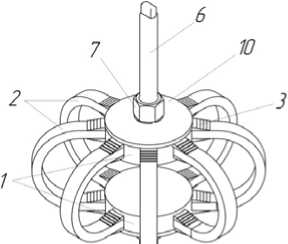
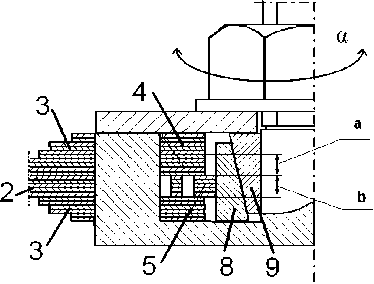
С целью подтверждения состоятельности теоретического исследования возможности управления демпфирующими характеристиками цельнометаллических виброизоляторов, был спроектирован и запатентован ленточный виброизолятор (см. рис. 12а), состоящий из двух разъемных обойм в виде тел вращения упруго соединенных между собой равномерно распределенными по окружности пакетами лент радиусного очертания. Пакеты лент включают в себя три различных набора лент. Один из наборов выполнен в виде волнистых по окружности шайб с выступами разной длины, второй набор лент выполнен в виде изогнутого по радиусу пакета лент, имеющих с двух концов фигурные выступы типа «ласточкин хвост» и жестко защемленных в обоймах виброизолятора, а третий из пакетов выполнен, как и предыдущий, с радиусным очертанием осевой линии, и установлен внутри второго. При этом на его концевых участках выполнены рамные упругие элементы в виде совпадающих по контуру с фигурными выступами второго набора очертаниями. Упругие выступы имеют возможность деформироваться с помощью набора из двух конических шайб, сопрягаемых по конусным поверхностям. Внешняя конусная втулка имеет разрез по вертикальной образующей, а ее цилиндрическая поверхность контактирует с выступами третьего набора, что дает возможность перемещения в радиальном направлении за счет того, что они закладываются в пазы обойм с зазорами (см. рис. 12б). Представленный ленточный виброизолятор, обеспечивает регулируемое прижатие слоев пакета друг к другу и стабильность демпфирующих свойств виброизолятора при его длительной работе.

б)

Рис. 12. Виброизолятор с возможностью управления характеристиками: а) виброизолятор в сборе; б) УДЭ виброизолятора в виде пакетов-рессор с разрезом

Выводы:

• 1.    Разработан ряд конструкций управляемых виброизоляторов на базе конструкционного демпфирования, с характеристиками, обеспечивающие эффективность виброизоляции на уровне от 82 до 99% и выше.

• 2.    Доказано, что организация параболического закона распределения трения в многослойной балке позволяет получить значения коэффициента рассеяния энергии ψ, близкие к теоретически возможным.

• 3.    В результате исследования математической модели многослойного ленточного упру-годемпфирующего элемента с управлением свойствами за счет угла его установки в зажимных обоймах установлено, что данная конструкция позволяет получить огромный диапазон рассеяния энергии: от работы в режиме практически без трения – «чистая упругость», до режима, когда упругость демпфера пренебрежимо мала в сравнении с силой трения – «чистый демпфер», без изменения его жесткостных и габаритных характеристик.

• 4.    Установлено, что в системе, состоящей из двух упругодемпфирующих элементов эллипсовидной формы, связанных стяжками переменной длины, на нагрузочных характеристиках можно получить области с жесткостью, близкой к квазинулевой, что открывает новые перспективы по разработке высокоэффективных средств виброзащиты.