Разработка и тестирование экспериментальной методики определения коэффициента теплопроводности наножидкостей

• 1.    Введение

• 2.    Теоретические основы метода нагреваемой нити

Интенсификация процессов теплообмена – одна из важнейших проблем современной энергетики. Во многих технологиях и оборудовании возникает потребность интенсивного отведения тепла. Одним из решений этой проблемы может стать использование в качестве теплоносителей жидкостей с присадками наночастиц (наножидкость [1]). Исследования теплообмена наножидкостей широко проводятся в последние 10–15 лет [2]. В результате показано, что наножидкости в некоторых случаях могут обладать уникальными тепловыми свойствами: имеют коэффициент теплопроводности на 20–40 % выше, чем жидкости, из которых они приготовлены, в 1,5–2 раза повышают величину критического теплового потока при кипении, на 10–30 % повышают значение коэффициента теплоотдачи при конвекции [2–5].

В настоящее время одним из важных фундаментальных вопросов является понимание механизмов переноса тепла в наножидкостях. Для объяснения аномальной теплопроводности наножидкостей анализируется несколько механизмов: броуновское движение наночастиц; образование высокотеплопроводного жидкого слоя на границе раздела «жидкость–частица»; кластеризация наночастиц; термодиффузия; баллистический перенос тепловой энергии и др. Вопрос о вкладе этих механизмов в эффективную теплопроводность различных наножидкостей остается открытым. В связи с этим общей теории, способной достоверно предсказывать теплопроводность наножидкостей, сегодня не создано. Поэтому при проведении исследований необходима надежная экспериментальная методика измерения коэффициента теплопроводности наножидкостей.

Таким образом, цель настоящей работы - разработка и описание экспериментальной методики определения коэффициента теплопроводности наножидкостей. Данная методика была разработана на основе известного нестационарного метода нагреваемой нити [6–7], c мостовой схемой Уитстона, который используется для определения коэффициента теплопроводности жидкостей.

Принцип измерения теплопроводности методом нагреваемой нити [6-7] основан на линейной зависимости между ростом температуры нити и логарифмом времени нагрева. В гомогенную исследуемую жидкость погружается нить, по ней пропускается постоянный электрический ток, тепловой поток на нити постоянный. Для идеального линейного источника основной процесс распространения тепла вокруг нити описывается уравнением Фурье [8]

— = a W д t со следующими граничными и начальными условиями:

A T ( r , t ) = 0 ( t < 0, при любом r ) , z^- d T ^        <7

l™ Ir "diГ n (r =0, t>0), lim AT (r, T)= 0 (r ^*, t > 0), r ^^

где A T - рост температуры нагретой нити; a - температуропроводность жидкости; X - теплопроводность жидкости; q - постоянный тепловой поток на единицу длины, выделяемый нагретой проволочкой.

Решением уравнения (1) является [8]

А = q  17 a 4 at )

^{А T (} r , t )    /1-Я-5 E 1 | ,.2 । ^,

4ПЛ   V r )

где E, В ) - j f eXLL ₌__Y_ in B + B + , ( B .) , , . b. C, B = 4-,, ^C = 1.78,.

Когда r равен радиусу нагретой нити r , который имеет очень маленькое значение (как и w

B ), то можно переписать так:

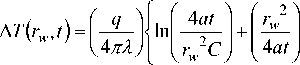
+ K > .

Для очень тонкой проволоки указанное решение может быть дополнительно упрощено. В итоге мы получаем следующее асимптотическое решение:

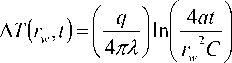
= H In t + A .

Уравнение (2) выражает линейную зависимость между A T и ln( ^ ). Реальное поведение температуры проволочки в процессе ее нагрева в эксперименте показано на рис. 1. Видно, что – 155 –

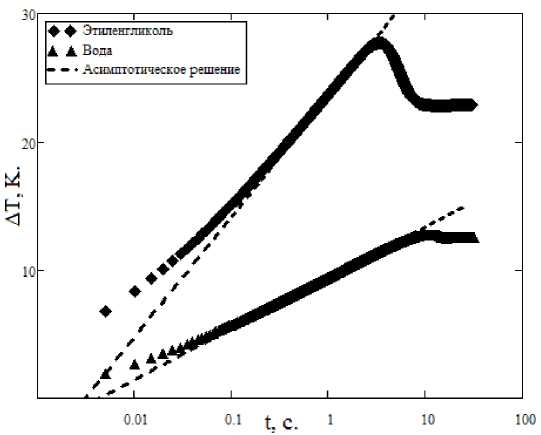
Рис. 1. Изменение температуры проволочки в процессе ее нагрева для линейной плотности теплового потока 14 Вт/м

существует участок температурной кривой, на котором поведение Δ T от ln( t ) действительно близко к линейному. Таким образом, теплопроводность жидкости может быть определена по наклону H и линейной плотности теплового потока с помощью следующего выражения:

Я =      ,

4nH где H - угол наклона прямой AT ~ ln(t).

. Описание экспериментальной установкии ее тестирование

Как уже было отмечено, методика измерения коэффициента теплопроводности основана на нестационарном методе нагреваемой проволоки. За основу установки принята мостовая схема Уитстона для измерения изменения электрического сопротивления нагретой проволоки. Фотография экспериментальной установки приведена на рис. 2.

Принципиальная электрическая схема установки показана на рис. 3. В эксперименте использовалась медная проволока длиной 80 мм и диаметром 75 мкм. Проволока погружалась в стеклянную емкость диаметром 5 см, содержащую 200 мл исследуемой жидкости. Проволочка ориентирована вертикально относительно вектора силы тяжести. Емкость с жидкостью была теплоизолирована при помощи поролона.

Проволока является одним из резисторов измерительного моста R w . Также используются резисторы: R ] = 2 кОм, R ₃ = 1 Ом и магазин сопротивлений R ₂, с помощью которого балансируется мост. Первоначально мост сбалансирован, и выходное напряжение на нем не превышает 10 мкВ. Для балансировки измерительной схемы от лабораторного источника тока GWInstek GPC-3060D в течение короткого периода времени подавали малое напряжение 0,1 В.

Рис. 2. Фотография экспериментальной установки

Изиерииль TPM-138

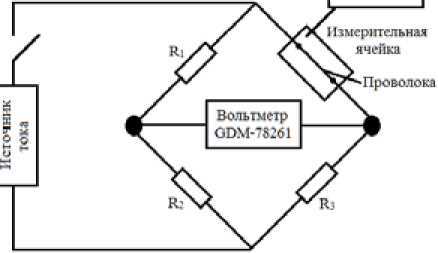
Рис. 3. Электрическая схема установки

В дальнейшем на схему подают измерительное напряжение и записывают изменение напряжение разбаланса мостовой схемы со временем. Входное напряжение от источника тока контролировали при помощи мультиметра APPA 109N. Измерения напряжения производили с помощью прецизионного вольтметра GWInstek GDM-78261 с шагом 10 мс. Кроме того, температуру исследуемой жидкости определяли при помощи хромель-копелевых термопар, подключенных к измерителю ТРМ-138.

Обработка полученных данных производилась по формулам, приведённым ниже. На-

R

^R w 0

R 3

чальное сопротивление проволоки находится из условия баланса мостовой схемы: —¹ =

R ₂

следовательно, сопротивление проволоки равно:

^R w 0

= R 1 R ■

^R 2   ³

Изменение сопротивления проволоки определяется как

R

R 3 R 1 ⁺ ( '     R 2* T out- )

^_ in_^

R ₂ - ( R , + R 2 )( V t )

_                                tn _ где Vin – подаваемое на схему напряжение; Vout – напряжение разбаланса.

Используя температурную зависимость электрического сопротивления меди, можно определить изменение температуры проволоки:

1 Rwt2 - Rwt 1 _ arw a   Rwо      aRwо ’ где a - температурный коэффициент сопротивления медной проволоки. Чтобы определить температурный коэффициент электрического сопротивления медной проволоки, предварительно выполнена специальная серия измерений сопротивления используемой проволоки при разных температурах. В результате этих измерений было установлено, что α = 0,000383 1/K.

Падение напряжение на проволоке определяется по формуле

V Rw =       '„

R wt ⁺ "  3

.

Тогда линейная плотность теплового потока на проволоке определяется как

(VRw)2 , q wTvwt где Lw – длина проволоки.

В итоге коэффициент теплопроводности жидкости, исходя из приведенной выше теории, определяется следующим образом:

х=

-9— = а. R4 1 4 n H       ^{w 0} 4п G ’

где G - угол наклона прямой A R ~ ln( t ).

Оценим относительную погрешность измерения коэффициента теплопроводности, которая складывается из погрешностей измерения плотности теплового потока q , температурного ^{коэффициента электрического} сопротивления ^a, начального сопротивления ^{проволочки} R 0 ^и угла наклона G .

5Х =

Вычисления показывают, что относительная ошибка измерения плотности теплового ^потока составляет 1,2 %, температурного коэффициента электрического сопротивления – 2 %, начального сопротивления проволочки – 1 % и угла наклона методом наименьших квадратов – 158 –

0,3 %. Таким образом, итоговая относительная погрешность измерения коэффициента теплопроводности жидкости δ λ данной методикой составляет 3 %.

Для тестирования и адаптации экспериментальной методики была проведена серия измерений на чистых эталонных жидкостях (вода и этиленгликоль). Для каждой жидкости измерения коэффициента теплопроводности проводили по 5 раз. Итоговые значения коэффициента теплопроводности получены усреднением по этим пяти измерениям. Все измерения проведены при комнатной температуре 25 °С.

Типичные экспериментальные кривые, полученные в одном из экспериментов, проиллюстрированы на рис 1. На графиках приведена зависимость температурного напора A T = T w - T f на проволочке от времени в процессе ее нагрева в воде и этиленгликоле, где T w – средняя по поверхности температура проволочки; T f – начальная температура жидкости. Для сравнения с результатами экспериментов на графиках также приведено асимптотическое решение (2), на котором основан метод нагреваемой проволоки.

Как видно из графиков, из-за отбрасывания нелинейных членов это асимптотическое решение дает расхождение с экспериментом в самом начале процесса теплопроводности. Это расхождение наблюдается примерно в течение 0,1 с для воды и 0,2 с для этиленгликоля после начала нагрева. Далее экспериментальные измерения и асимптотическое решение практически совпадают. Это совпадение продолжается до тех пор, пока вокруг проволочки не сформируется достаточно интенсивное свободно-конвективное течение. В результате этого температура проволочки в эксперименте становится значительно ниже, чем дает асимптотическое решение, учитывающее только процесс теплопроводности. В зависимости от жидкости момент времени, когда свободная конвекция начинает доминировать над теплопроводностью, наступает примерно через 3 с для этиленгликоля и через 7 с для воды. Такое сильное расхождение во временах начала свободной конвекции в воде и этиленгликоле на первый взгляд кажется парадоксальным. Ведь вязкость этиленгликоля примерно в 17 раз выше вязкости воды, и, казалось бы, свободная конвекция в этиленгликоле должна начинаться значительно позже, чем в воде. Однако в эксперименте наблюдается совершенно противоположная картина. Это связано с тем, что из-за плохой теплопроводности этиленгликоля температура проволочки в нем возрастает гораздо быстрее, чем в воде. Из-за этого и интенсивность свободной конвекции в нем существенно выше, чем для воды в аналогичный момент времени.

В методических целях были проведены исследования влияния ориентации проволочки на время возникновения свободной конвекции в процессе ее нагрева. В результате этого было установлено, что при горизонтальном расположении проволочки свободная конвекция возникает значительно раньше, чем при вертикальном расположении. Так, для воды при линейной плотности теплового потока 13 Вт/м свободная конвекция начинает доминировать над теплопроводностью через 2,2 с после начала нагрева для горизонтальной проволоки и через 7,5 с – для вертикальной. Поэтому вертикальная ориентация проволочки предпочтительнее.

Кроме того, были проведены исследования влияния плотности теплового потока на проволочке на время возникновения свободной конвекции. Было показано, что с уменьшением плотности теплового потока существенно увеличивается время существования режима «чистой» теплопроводности. Так, например, для воды при линейной плотности теплового потока, равной 4,33 Вт/м, и горизонтальном расположении проволоки, свободная конвекция пренебрежимо – 159 – мала по сравнению с теплопроводностью до 3,5 с после начала нагрева, а для вертикального – до 12 с. Однако вместе с этим значительно уменьшился нагрев поверхности проволочки и, соответственно, уменьшилось изменение электрического сопротивления, вызванное нагревом проволоки. Изменение электрического сопротивления проволоки является, по сути, единственной инструментально измеряемой в эксперименте величиной, поэтому снижение плотности теплового потока приводит к ухудшению чувствительности метода. Исходя из этого, при проведении экспериментов в качестве оптимальных значений линейной плотности теплового потока выбирали значения в диапазоне от 12 до 15 Вт/м.

В табл. 1 и 2 приведены итоговые результаты измерений коэффициента теплопроводности воды и этиленгликоля и сопоставление их со справочными данными.

Эти результаты получены для вертикальной ориентации проволочки в пространстве и линейной плотности теплового потока в диапазоне от 13 до 14 Вт/м. Как видно, получено достаточно хорошее согласие измеренного коэффициента теплопроводности с литературными данными [9–10]. Для воды максимальное расхождение составляет 2 %, для этиленгликоля – 3 %. Такое расхождение находится в пределах инструментальной погрешности метода.

При помощи данной методики были проведены измерения коэффициента теплопроводности наножидкости на основе наночастиц оксида алюминия и оксида меди, которые являются наиболее исследованными. Несущей жидкостью был этиленгликоль. Объемная концентрация варьировалась от 0,5 до 2 %. Для приготовления наножидкости применяли стандартный двухшаговый процесс. После добавления в этиленгликоль необходимого количества нанопорошка емкость с наножидкостью на полчаса помещали в ультразвуковой диспергатор Сапфир для

Таблица 1. Измеренные значения коэффициента теплопроводности воды при температуре 25 °С

№ опыта	λ изм , Вт/(м×К)	λ справ [9], Вт/(м×К)	Отклонение, %
1	0,610	0,607	0,5
2	0,608		0,2
3	0,619		2,0
4	0,612		0,8
5	0,616		1,4

Таблица 2. Измеренные значения коэффициента теплопроводности этиленгликоля при температуре 25 °С

№ опыта	λ изм , Вт/(м×К)	λ справ [10], Вт/(м×К)	Отклонение, %
1	0,260	0,254	2,3
2	0,261		2,7
3	0,251		1,2
4	0,259		1,9
5	0,262		3,1

а)

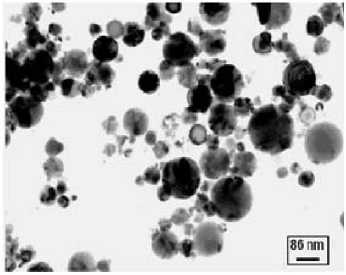
Рис. 4. Микрофотографии наночастиц оксида алюминия (а) и оксида меди (б)

б)

разрушения конгломератов наночастиц. Наночастицы оксида алюминия были приобретены у компании «Плазмотерм» (Москва). По данным рентгенофазового анализа, удельная поверхность порошка составила 30 м2/г, что соответствует среднему размеру наночастиц 50 нм. Нанопорошок оксида меди произведен ООО «Передовые порошковые технологии» (Томск). Наночастицы сферические, насыпная плотность порошка равна 2,2 г/см3. Средний размер наночастиц равнялся 55 нм. Микрофотографии наночастиц оксида алюминия и оксида меди приведены на рис. 4.

Измерения коэффициента теплопроводности для каждой концентрации наночастиц проводили по 10 раз. Итоговые значения коэффициента теплопроводности получены усреднением по 10 измерениям. Разброс результатов от среднего не превысил 3 %. Все измерения проведены при комнатной температуре 25 °С.

Типичное поведение линейной плотности теплового потока на проволочке и изменение электрического сопротивления проволочки от времени для различных наножидкостей изображено на рис. 5, 6.

Используя эти данные, по формуле (4) определили значения коэффициента теплопроводности для каждой из наножидкостей. Зависимость измеренного эффективного коэффициента теплопроводности от концентрации наночастиц оксида алюминия в этиленгликоле показана на рис. 7.

На рис. 8 приведена зависимость измеренного эффективного коэффициента теплопроводности от концентрации наночастиц оксида меди в этиленгликоле.

Под эффективным коэффициентом здесь понимается отношение коэффициента теплопроводности наножидкости к коэффициенту теплопроводности базовой жидкости. Для сравнения представлены результаты известных из литературы измерений, полученных другими авторами [11–16]. Как видно из графика на рис. 7, наблюдается хорошее согласие наших измерений с результатами большинства зарубежных данных. Разброс экспериментальных данных коэффициента теплопроводности, полученных различными авторами, в целом отражает современное состояние исследований в области теплообмена наножидкостей. Отсутствует повторяемость результатов, эксперименты часто противоречат друг другу. И это при том, что наножидкость на основе оксида алюминия наиболее изучена. Для наножидкости на основе оксида меди в

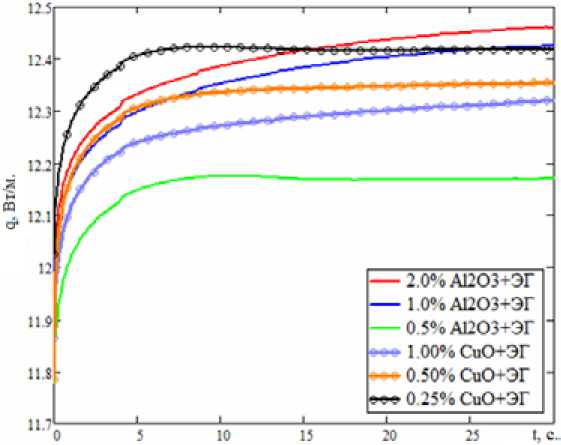
Рис. 5. Линейная плотность теплового потока на проволочке

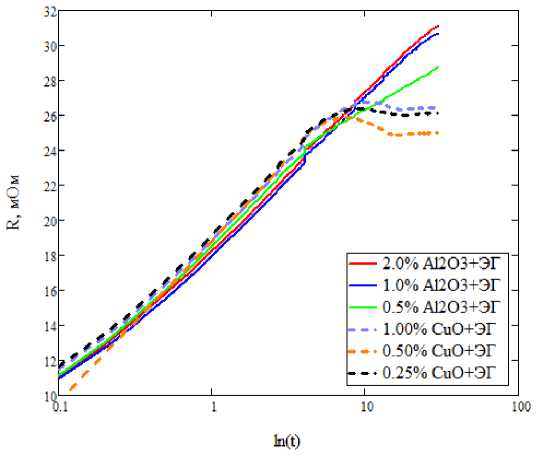
Рис. 6. Изменение электрического сопротивления проволочки этиленгликоле данных для сравнения существенно меньше, чем для оксида алюминия. Здесь для сравнения на рис. 8 приводим данные из работы [17]. В этой работе использовались наночастицы оксида меди размерами 33 нм. Как видно из графика, согласие наших данных с измерениями [17] вполне удовлетворительное.

Для сравнения с экспериментами на графиках также приведены значения коэффициента теплопроводности, получаемые по корреляции Максвелла [17]:

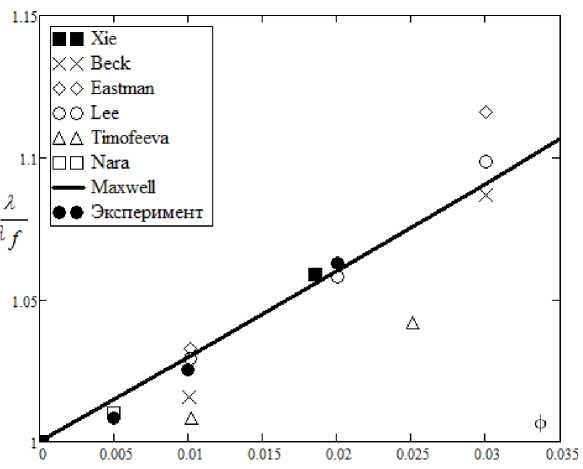
Рис. 7. Зависимость измеренного коэффициента теплопроводности от концентрации наночастиц оксида алюминия в этиленгликоле при температуре 25 °С

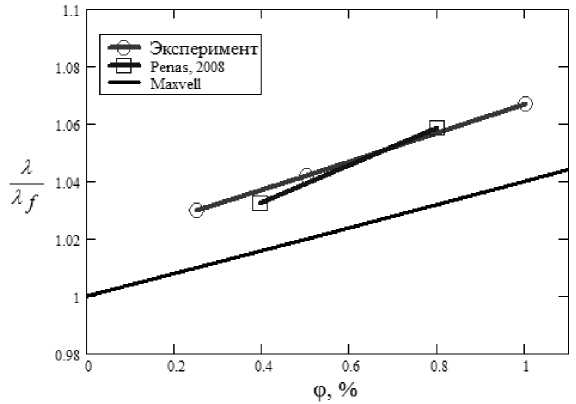
Рис. 8. Зависимость измеренного коэффициента теплопроводности от концентрации наночастиц оксида меди в этиленгликоле при температуре 25 °С

x x p + 2х f + 2ф(х p -х f) xf xp+2хf -ф(хp -xf) ’ где λP, λf – коэффициенты теплопроводности материала частиц и базовой жидкости.

Модель Максвелла была разработана для определения эффективной теплопроводности суспензии типа «жидкость - твердое тело» при низких объемных концентрациях частиц сфе-– 163 – рической формы. Эта модель применима к статистически однородной суспензии «жидкость – твердое тело» с малой объемной концентрацией при хаотически рассеянных и равномерно распределённых по размерам сферических частицах. В большинстве случаев коэффициент теплопроводности наножидкости превышает значения, предсказываемые корреляцией Максвелла. В наших исследованиях это хорошо видно для наножидкости на основе оксида меди (рис. 8). Однако для наножидкости на основе оксида алюминия и этиленгликоля было установлено, что корреляция Максвелла в исследованном диапазоне концентраций хорошо описывает экспериментальные данные. Вероятно, это связано с тем, что использованный для исследований нанопорошок оксида алюминия имел достаточно большой разброс частиц по размерам. На рис. 4а видим, что наряду с мелкими частицами присутствует довольно много крупных частиц с размерами более 100 нм. Наличие крупных частиц приводит к тому, что зависимость теплопроводности наножидкости стремится к классической максвелловской зависимости.

Заключение

В данной статье разработана и протестирована методика определения коэффициента теплопроводности на основе нестационарного метода нагреваемой нити. Тестирование экспериментальной методики было проведено на измерении теплопроводности воды и этиленгликоля. Расхождение измерений с эталонными данными не превысило 3 %. При помощи разработанной методики были проведены измерения коэффициента теплопроводности наножидкости на основе наночастиц оксида алюминия и оксида меди. Несущей жидкостью был этиленгликоль. Объемная концентрация варьировалась от 0,25 до 2 %. Результаты измерений сопоставлены с известными измерениями других авторов и корреляцией Максвелла. Получено хорошее согласие результатов.

В заключение отметим еще одно важное обстоятельство. При анализе результатов экспериментов, полученных методом нагреваемой проволочки, высказываются опасения относительно того, что в процессе измерений коэффициента теплопроводности наножидкости на поверхности проволочки осаждаются наночастицы, в результате чего со временем измерения значительно искажаются. Эти сомнения были опровергнуты нами экспериментально. После многократных измерений в наножидкостях с различной концентрацией вновь были проведены измерения на чистых жидкостях. Никаких отклонений измеренного коэффициента теплопроводности от полученных ранее значений не установлено. Таким образом, в результате проведенной работы создана и протестирована экспериментальная установка, позволяющая с приемлемой точностью определять значения коэффициента теплопроводности жидких сред. Показана ее применимость к измерению теплопроводности наножидкостей. В дальнейшем данная методика будет применена для систематических исследований коэффициента теплопроводности различных наножидкостей.

Работа выполнена при частичной финансовой поддержке Российского научного фонда (соглашение № 14-19-00312), а также в рамках гос. задания МОН РФ СФУ на 2014 г.