Разработка и тестирование объекта системы динамического анализа механизмов (dam) ©

в

Рис. 1. Объект – коромысло:

а – обозначение на объектном представлении механизма ( i- ый объект), б – кинематическая схема, в – динамическая модель

Уравнение движения масс динамической модели (рис. 1 в ):

' J 1 ^р = - c ( р - U i ( р )) - b ^{( р} - UX T k ^{) р} _к ) +

+ С 2(^2 - Рр + Ь2(р2 - Фх) + W1

J 2 Р 2

+ c з^{( р} з ^{- р} 2 ) + b з^{( р} & з ^{- р} 2 ) + W ,

_J»Pn = — cn (Рп — Р»-1) — bn (<Рn — ^Рn-1 ) + Wn + ^/ где n – число сосредоточенных масс, моделирующих рассматриваемый объект (вращающийся рычаг). Очевидно, чем больше n, тем точнее модель будет описывать объект, естественно, в случае достоверности значений её прочих параметров. Таким образом, если в качестве математической модели вращающегося рычага использовать уравнения (1), будем иметь:

• ■    Входные параметры: Ф к , ф к - перемещение и скорость предшествующего ему k -го объекта; Ω j – возмущение со стороны j -го объекта, следующего за рассматриваемым (2); W m

  – ( m =[1, 2, …, n ] – внешние нагрузки. Это момент, приложенный к m -ой массе модели.

• ■    Выходные параметры: Ф i , Ф i - перемещение и скорость объекта; Ω i – отклик на возмущение предшествующего объекта (2), δ , δ max , σ – точность позиционирования рычага, её максимальное и среднее значения (3).

Ωi =[c1(ϕ1 -Ui(ϕk))+b1 (ϕ

1Tδ=ϕn -Ui(ϕk), δmax = max(ϕn -Ui(ϕk)), σ= ∫ϕn - Ui(ϕk(t)) dt. T0

Характеристики вида (3) служат для оценки уровня протекающих в объекте динамических процессов. В данной работе они будут использоваться для тестирования моделей. ■ Свойства: N - число масс динамической модели (рис. 1 в ); J m – моменты инерции фрагментов рычага относительно осей их вращения ( J m = const ); c m , ψ – упруго-инерционные характеристики связей, соединяющих фрагменты рычага ( c m = const при m≠1); η i – зазор в соединении рассматриваемого объекта с предыдущим; U i ( ϕ k ), U i ^′ ( ϕ k ) – функция положения рычага и её производная. Для определения величин c 1 , b m используются зависимости, приведённые в работах [1, 2].

Пригодность любой модели для её использования в системе ( dam ), будем проверять по следующим показателям: сложность, устойчивость, границы применимости. В качестве тестового звена, которому в частности соответствует исследуемый объект, выберем консольную вращающуюся балку в форме прямоугольного сечения высотой в два раза больше ширины, перемещающуюся по гармоническому закону вида:

U = ^π ⋅ sin2 πν t , 2

π

U′ = ⋅ cos 2πνt.

Если принять в качестве эталона данные, полученные на основе десятимассовой модели, то относительная погрешность расчётов для одномассовой и двухмассовой моделей составит соответственно: для δ max – ≈15,9% и ≈16,2%, для σ – ≈16,3% и ≈20%. Таким образом, как следует из приведённых выше зависимостей для получения результатов приемлемой точности по перемещениям и скоростям вполне достаточно одномассовой модели. Эта же модель позволяет оценить уровень нагрузок в рычаге и, к сожалению, непригодна для вычисления ускорений. Следует отметить, что учёт сил сопротивления позволяет резко повысить сходимость результатов (рис. 3). Так, при ψ =0,4 относительная погрешность для δ max не превышает 0,4%, а для σ – 6%.

Анализ приведенных зависимостей (см. рис. 2, 3) показывает, что для данного скоростного режима, значений упруго-инерционных характеристик и величине замыкающего момента имеет место разрыв в кинематической паре объекта. Если это реальный кулачковый механизм, то в процессе его работы ролик коромысла постоянно «стучит» по дорожке кулачка. Очевидно, что о работоспособности механизма в этом случае говорить не приходится. Исправить положение можно различными способами, например, увеличить замыкающий момент (рис. 4).

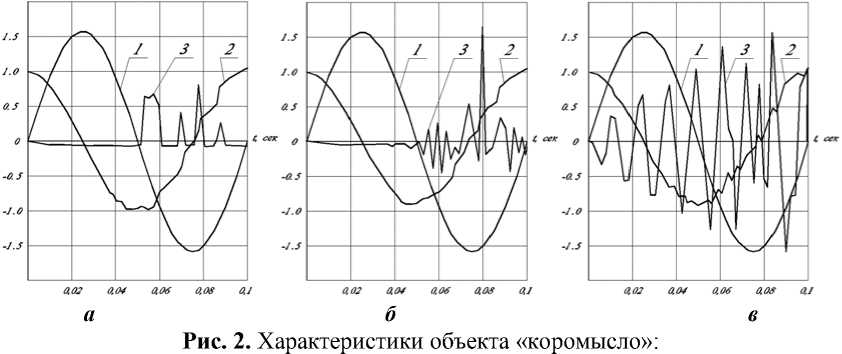
а – одномассовая, б – двухмассовая, в - десятимассовая модели: 1 – перемещение (∙1 рад), 2 – скорость (∙10 ² рад∙сек^-1), 3 – ускорение (∙10 ⁵ рад∙сек^-2)

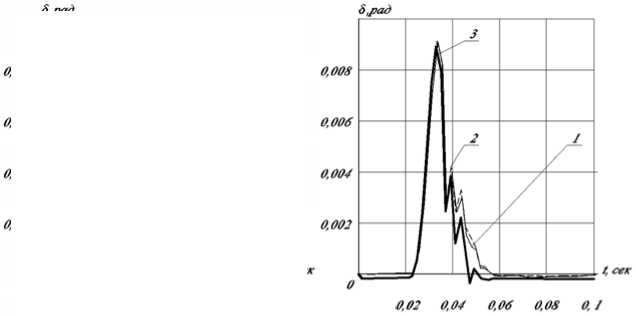
б

Рис. 3. Точность позиционирования объекта:

а – ψ =0, б – ψ =0,4; 1 – одномассовая модель, 2 – двухмассовая модель, 3 – десятимассовая модель

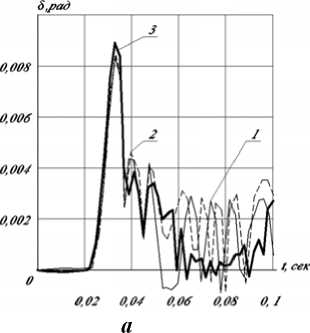
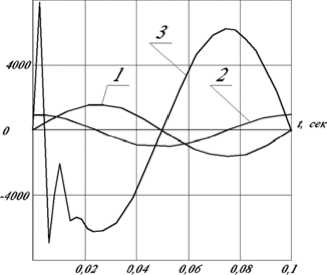
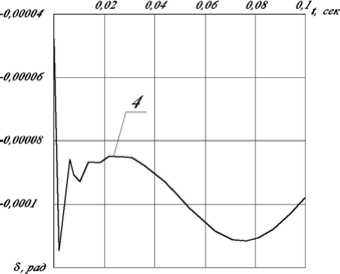
Рис. 4. Кинематические характеристики объекта (M=1000, ψ =0,4 – десятимассовая модель):

1 – перемещение (∙10-3 рад), 2 – скорость (∙10-1 рад∙сек-1), 3 – ускорение (∙1 рад∙сек-2), 4 – точность позиционирования (∙1 рад)

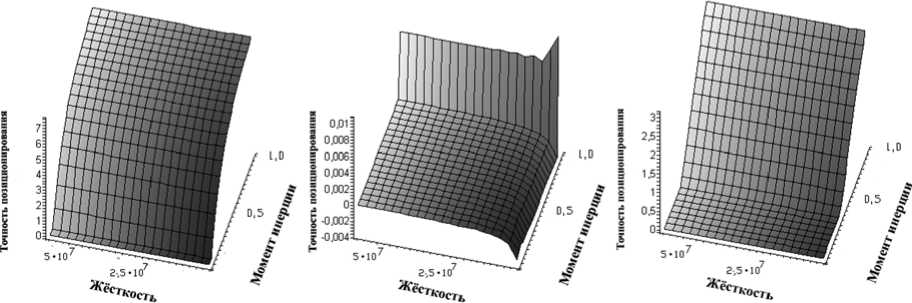
Для определения границ применимости, в которых модель устойчива, исследуем её поведение в следующих диапазонах изменения значений упруго-инерционных параметров: моментов инерции J=[0,05, 1,0] кг/м2, жёсткостей – c=[0,25 107, 5,0 107 Нм/рад. На рис. 5 изображены графики функции δmax(J,c) при различных замыкающих моментах и скоростных режимах. Для их построения была использована двухмассовая модель. Анализ приведенных зависимостей показывает, что при изменении параметров модели в исследуемых пределах зоны потери её устойчивости отсутствуют. Достаточно резкий рост δmax(J,c) (рис. 5 а, б, в) связан с разрывами в кинематической цепи объекта. Такую ситуацию следует расценивать как потерю работоспособности механизмом, которому соответствует данный объект.

б                            в

а

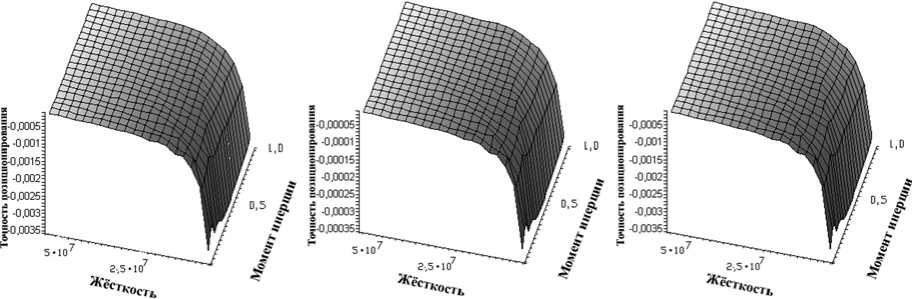
г                              д                      е

Рис. 5. К расчёту устойчивости модели: а – ν =1, М=600; б – ν =5, М=600, в – ν =10, М=600; г – ν =1, М=6000, д – ν =5, М=6000, е – ν =10, М=6000.