Разработка информационной системы для нахождения упругопластической границы стержней прокатного профиля

Введение. Нахождение упруго-пластической границы в скручиваемых металлических стержнях – важная научная задача. Ее решение, с одной стороны, позволяет более точно определять прочностные характеристики скручиваемого стержня, которые широко используются в различных конструкциях и механизмах. А это, в свою очередь, приводит к облегчению конструкций и повышает их эксплуатационные характеристики. С другой стороны, пластические деформации, которые возникают при скручивании, приводят к упрочнению стержней. Такой процесс широко используется в промышленной обработке элементов конструкций. При этом очень важно, чтобы пластическому деформированию подвергались только близкие к внешней поверхности слои металла и чтобы в процессе деформирования не произошло разрушение упрочняемого изделия и не ухудшились его эксплуатационные характеристики.

Перечисленные проблемы приводят к задаче нахождения упруго-пластической границы скручиваемых стержней [1]. До работ авторов [2–4] не существовало метода, который позволял бы решать эту задачу для стержней прокатного профиля. Использование законов сохранения для решения дифференциальных уравнений пластичности и упругости позволило получить аналитические формулы для нахождения упруго-пластической границы скручиваемых стержней. А это, в свою очередь, привело к созданию информационной системы, которая позволила бы использовать результаты научных исследований в практической работе инженеров-расчетчиков.

В работе [2] предложены формулы для аналитического определения величины касательных напряжений т xz = и , т _yz = v во всех внутренних точках стержня для случая кусочно-гладкой ориентированной границы поперечного сечения. Эти формулы выводятся из закона сохранения для уравнений упругости и пластичности и имеют вид

( А 1 J z( ^{f (} t ^)- x 0 ) V ^{( f} ' ( t ^{) ) 2 +} (Ф ' ⁽ t ^{) ) 2} u ( x 0. У 0 ) = - I ⁽----/ _{z x} 2       , _x 2

^П 0    V⁽ f ( t ) - x 0 ) + ^(ф ( t ) - y 0 )

+ af ' ( t ) arctg ^ф ( t ) y ⁰ ) dt ;

f ( t ) - X 0

f £ J ( Ф ( t )-У 0 ) У( f'( t ))2 + (Ф‘( t ))2 v ( x 0.y 0 )       I( n 0   V(f(t)-X0) + (ф(t)-y0)

+af ‘(t) ln(( f (t)-x 0)2+( ф (t)-y 0)2) dt, где a = -2G9 ; 9 - постоянная; G - модуль упругости при сдвиге; x = f(t), y = φ(t) 0 ≤ t ≤ T – уравнение граничного контура.

Точки, в которых выполняется условие и ² + v ² > 1, принадлежат пластической области, а те, в которых это выражение меньше единицы, – упругой.

Разработка информационной системы. Разнообразие видов поперечных сечений стержней и параметра, характеризующего кручение, требует сложных аналитических вычислений для каждого нахождения упруго-пластической границы стержня при кручении.

В [3; 4] авторами написаны программы для ЭВМ, позволяющие находить упруго-пластическую границу для стержней некоторых сечений при кручении.

Использование этих программ для расчетов показало, что непосредственное их применение не совсем удобно и требует дополнительной работы программиста, поэтому на их базе было решено разработать информационную систему для нахождению упругопластической границы стержней различных прокатных профилей, наиболее часто встречающихся на практике.

При разработке информационной системы пришлось столкнуться как с проблемами технического характера (выбор языка программирования, написание алгоритмов), так и с приведением формул расчета, выведенных авторами [2], к виду, приемлемому для использования в алгоритмах.

Первые расчеты производились с использованием системы компьютерной алгебры Sage [5; 6] – открытого программного обеспечения, альтернативного системам Magma, Maple, Mathematica и MATLAB.

Символьные вычисления – это преобразования и работа с математическими равенствами и формулами как с последовательностью символов. Они отличаются от численных расчётов, которые оперируют приближёнными численными значениями, стоящими за математическими выражениями. Системы компьютерной алгебры могут быть использованы для символьного интегрирования и дифференцирования, подстановки одних выражений в другие, упрощения формул и т. д.

Компьютерная алгебра (в отличие от численных методов) занимается разработкой и реализацией аналитических методов решения математических задач на компьютере и предполагает, что исходные данные, как и результаты решения, сформулированы в аналитическом (символьном) виде.

Выбор был сделан в пользу Sage, так как планировалось, что в будущем будет создаваться информационная система. В системе компьютерной алгебры Sage используется язык программирования Python [7–9], и алгоритмы, написанные для Sage, можно использовать при разработке информационной системы при минимальных изменениях. Помимо этого, был произведен анализ готовых библиотек, предоставляющих возможность использовать символьные вычисления. Была выбрана библиотека SymPy [10; 11], которая представляет собой открытую библиотеку символьных вычислений на языке Python.

Планировалось, что информационная система будет со временем развиваться – возможно добавление новых видов профилей, например с отверстием. Поэтому при создании информационной системы встал выбор, в каком виде создавать информационную систему.

В [12; 13] рассматривается, что в настоящее время активно развивается технология, получившая название облачные вычисления (Cloud Computing). Основная ее идея – предоставить пользователю программные и компьютерные ресурсы как интернет-сервисы, расположив при этом все приложения и их данные, необходимые для работы, на удаленном сервере в Интернете.

Различные модели облачных вычислений представлены на рис. 1. Software as a Service (SaaS) и Platform as a Service (PaaS) предоставляют программные компоненты, остальные – аппаратное обеспечение, серверы, сети и пр. SaaS объединяет так называемые законченные приложения, например, почтовые клиенты, текстовые и табличные редакторы, редакторы презентаций, карты различного назначения, онлайновые платежные системы, игры, виртуальные миры, поисковые системы, чаты и др. В отличие от SaaS, предназначенной для конечного пользователя, PaaS предоставляет сервисы разработчикам программного обеспечения.

Типичными примерами сред, представленных на рынке и основанных на концепции облачных вычислений, являются: Amazon AWS, Microsoft Azure, Google App Engine, Stax, 10gen, Google Wave, Force.com и др. Эти среды предназначены для профессиональных разработчиков программного обеспечения, поддерживают один или несколько языков программирования и, в некоторых случаях, специализированную платформу для разработки. Эти среды являются либо универсальными, либо ориентированы на какой-либо тип приложений. Так, универсальная среда Google App Engine поддерживает язык программирования Python и Java. Предлагаемая компанией среда исполнения включает полную реализацию возможностей самого языка Python и большинство функций из стандартной библиотеки языка. Универсальные среды Engineyard.com и Heroku.com. Engineyard, основанные на Amazon EC2 и Amazon S3, поддерживают язык программирования Ruby, Azure Services Platform предоставляет майкрософт-ориентированную инфраструктуру и инструменты разработки: в ней изначально присутствует поддержка Windows, NET Framework и среды разработки Visual Studio. Эта среда также поддерживает PHP, MySQL, Ruby, Python, Java, Eclipse и Zend.

Программное обеспечение как сервис (Software as a Servece)

Платформа как сервис (Platform as a Servece)

Инфраструктура как сервис (Infrastructure as a Servece)

Центр обработки и хранения данных (Data Center - Hardware, Servers, Networking)

Рис. 1. Модели облачных вычислений [14]

При разработке было решено использовать среду Google App Engine (GAE), так как она предоставляет возможность использовать язык Python и библиотеку Sympy при разработке информационной системы [15]. В связи с тем, что математические расчёты крайне требовательны к аппаратным ресурсам, а у среды GAE есть ограничения для бесплатной версии [16], было решено развернуть GAE на локальном сервере. К примеру, время построения упруго-пластической границы при кручении стержня с сечением вида двутавр составляет около 20 мин на рабочей станции с четырехядерным процессором Intel Core i5 – 3330.

Такое решение позволило максимально упростить доступ к информационной системе – любой человек, имеющий персональный компьютер или даже мобильное устройство, через веб-браузер получает доступ к информационной системе.

ПОСТРОЕНИЕ УПРУГО-ПЛАСТИЧЕСКОЙ ГРАНИЦЫ

ВЫБЕРИТЕ ВИД СЕЧЕНИЯ СТЕРЖНЯ

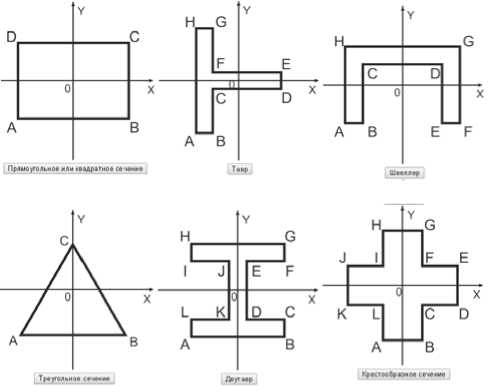
Рис. 2. Начальный интерфейс автоматизированной системы научных исследований по нахождению упруго-пластической границы стержней различных сечений

На рис. 2 представлен начальный интерфейс информационной системы для нахождения упругопластической границы стержней различных сечений. На рис. 3 представлен интерфейс задания границы стержня крестообразного сечения. На рис. 4 представлена расчетная задача для стержня прямоугольного сечения при a = –1,6. На рис. 5 представлена расчетная задача для стержня с треугольным сечением при a = –4,2. На рис. 6 представлена расчетная задача для стержня крестообразного сечения при a = –0,5. На рис. 7 представлен интерфейс задания границы для стержня с сечением вида тавр при a = –0,7. На рис. 8 представлена расчетная задача для стержня с сечением вида двутавр при a = –1,4. На рис. 9 представлена расчетная задача для стержня с сечением вида швеллер при a = –0,5. Звездами выделена пластическая область, круглыми точками – упругая область.

Примечание . При работе программы пластическая область выделяется красным, а упругая – синими точками.

Заключение. Приведенная в работе информационная система является полезным инструментом при экспериментальном определении упруго-пластических границ, поскольку из-за различных вкраплений и дефектов ее очень трудно определить визуально даже при наличии большого опыта проведения такого рода экспериментов. Работа в этом направлении еще не закончена. Следующим шагом будет информационная система, котор ая позволит определять упругопластические границы для стержней, сечение которых не является односвязным.

ПОСТРОЕНИЕ УПРУГО-ПЛАСТИЧЕСКОЙ ГРАНИЦЫ

ДЛЯ СТЕРЖНЯ КРЕСТООБРАЗНОГО СЕЧЕНИЯ

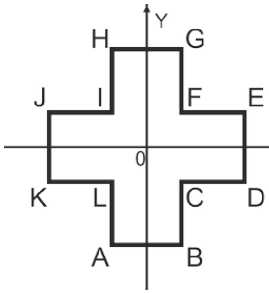
Пример! Примера Примерз Пр и мер 4 Центр тяжести фигуры должен распологаться в точке (0;0).

Введите координаты точек А, В', С, D, Е, F, G, Н как на рисунке выше.

Время расчета может занимать длительное время. Время расчета каждого из приведенных примеров около 14 минут.

АС ЕЕ ЭС ЕЕ Е^СЕ ЕЕ Е=Е ЕЕ Е^еЕ ЕЕ Е^еЕ ЕЕ :

^GE ЕЕ Е^нЕ ЕЕ Е^тЕ ЕЕ Е ^jE ЕЕ Е^еЕ ЕЕ E^lE ЕЕ :

Введите параметр характерезующий кручение, меньше О

Красные точки соответствуют пластической области, синие - упругой области

Построить границы

Вернуться к выбору вида стрежней

Рис. 3. Интерфейс задания границы

-2-1012

Рис. 4. Упруго-пластические границы стержня с прямоугольным сечением

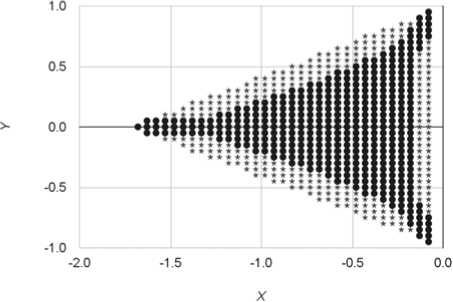
Рис. 5. Упруго-пластические границы стержня с треугольным сечением

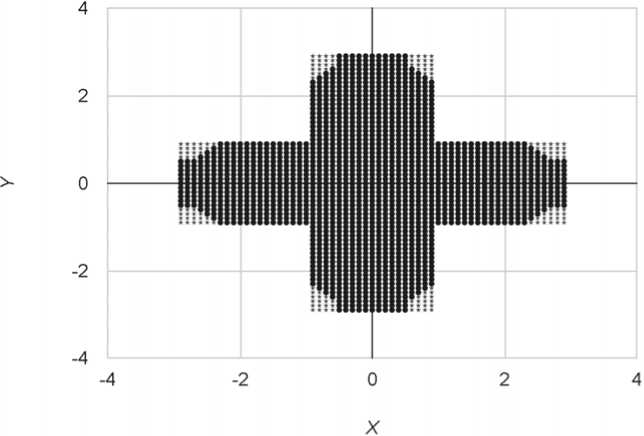
Рис. 6. Упруго-пластические границы стержня крестообразного сечения

4  .........

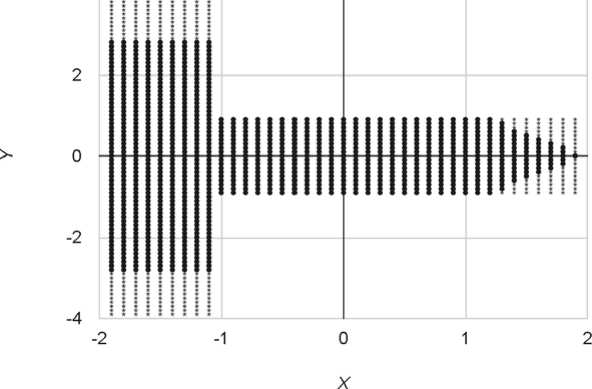
Рис. 7. Упруго-пластические границы стержня с сечением вида тавр

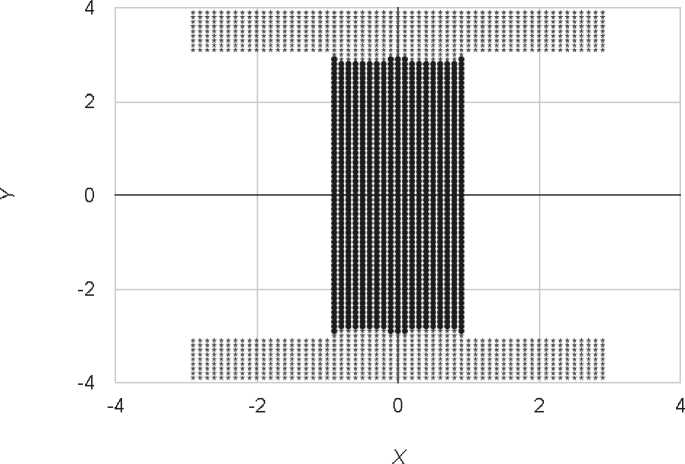
Рис. 8. Упруго-пластические границы стержня с сечением вида двутавр

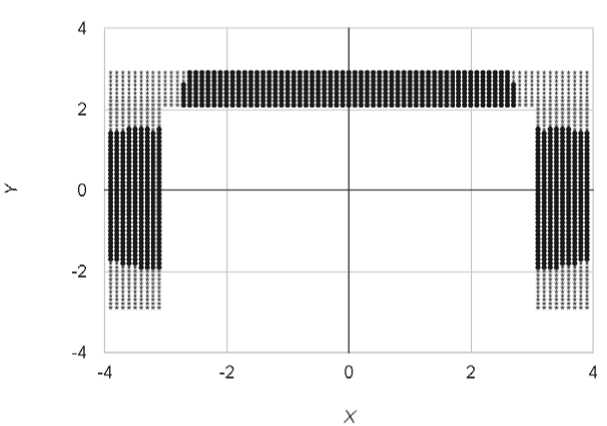
Рис. 9. Упруго-пластические границы стержня с сечением вида швеллер

Acknowledgments. This work was supported by the Ministry of Education and Science of the Russian Federation № Б -180-14.