Разработка интеллектуального алгоритма управления объектами типа перевернутый маятник
Автор: Золотов Александр Валентинович
Журнал: Горные науки и технологии @gornye-nauki-tekhnologii
Статья в выпуске: 8, 2012 года.
Бесплатный доступ
В данной статье рассматривается вопрос разработки алгоритма нечеткого управления объектами типа перевернутый маятник. Задача стабилизации перевернутого маятника является классической в теории автоматического управления. Но в нашем случае она решается при помощи нечеткого регулирования, которое является одним из современных актуальных технологий управления. Приводится анализ системы и ее математическая модель. Выполняется синтез нескольких нечетких регуляторов в среде MATLAB Fuzzy Logic Toolbox. Приводится моделирование автоматического регулирования средствами MATLAB Simulink и схемы моделирования. Приводятся результаты моделирования и выводы на их основе.
Автоматизация, интеллектуальное управление, нечеткая логика, перевернутый маятник, моделирование
Короткий адрес: https://sciup.org/140215553
IDR: 140215553 | УДК: 001.8
Текст научной статьи Разработка интеллектуального алгоритма управления объектами типа перевернутый маятник
- mL ф 2cos
Подставив выражение для H(t) из уравнения (5) в уравнение (4), получим:
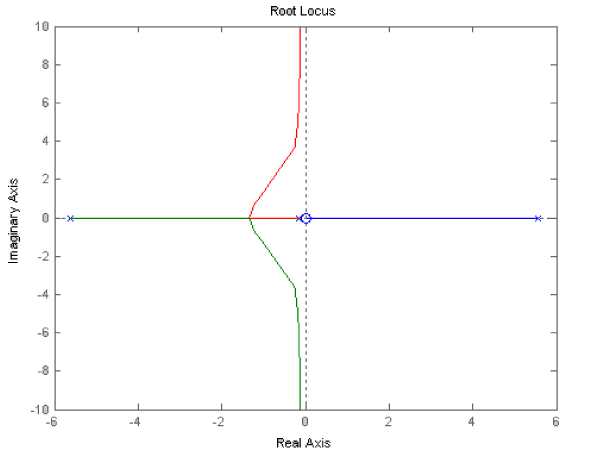
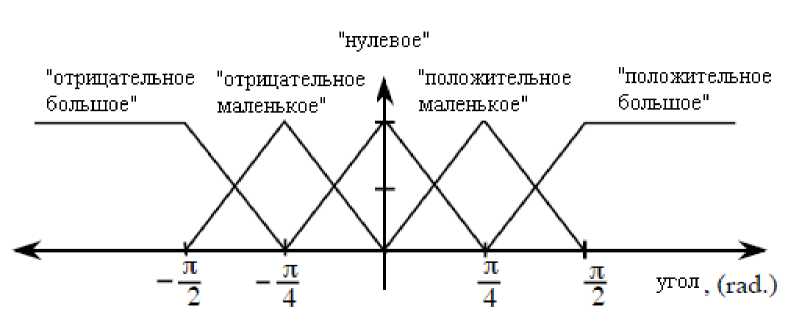
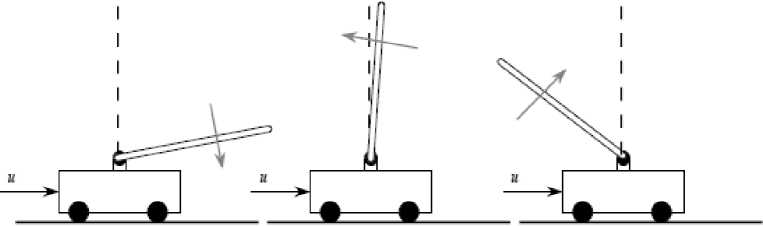
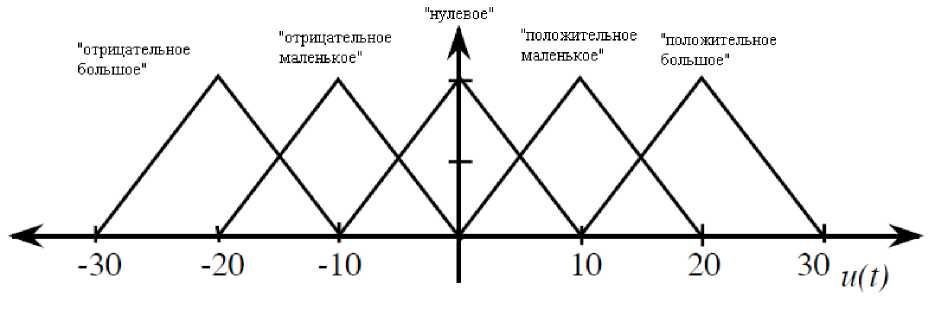
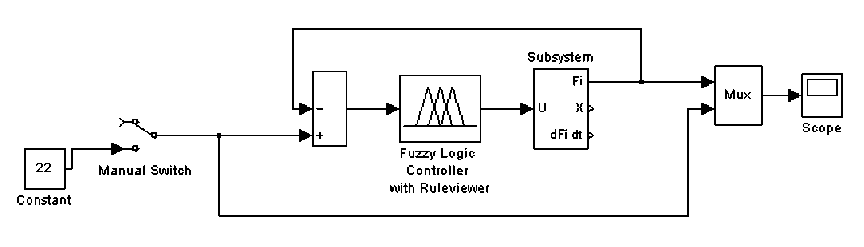
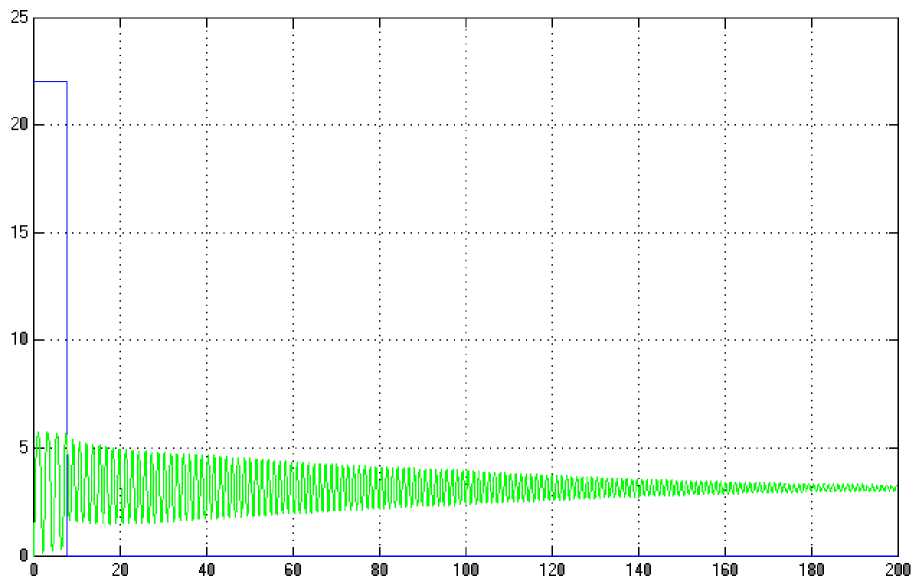
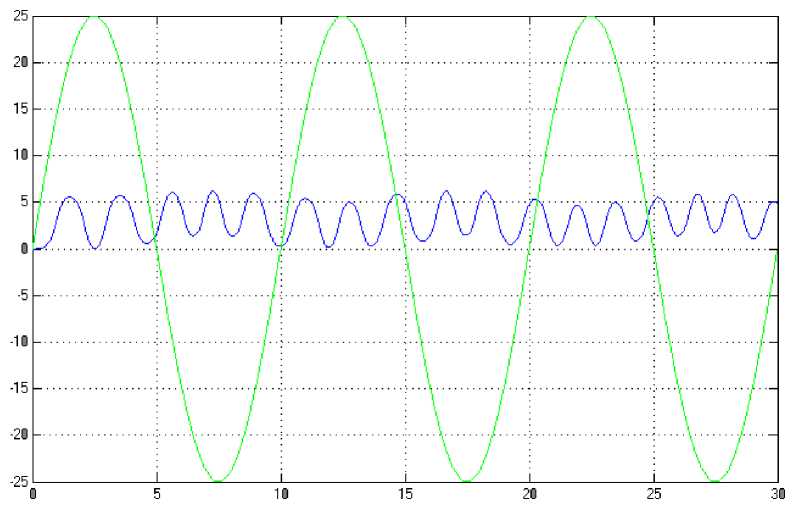
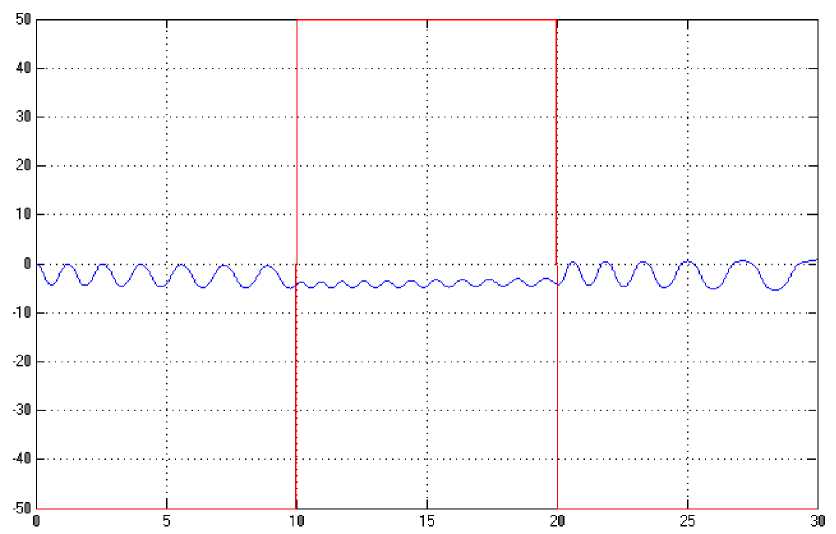
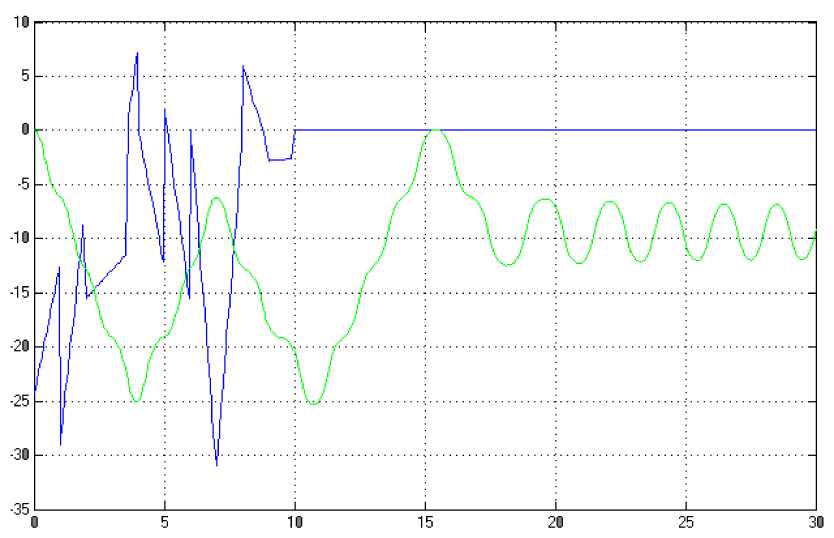
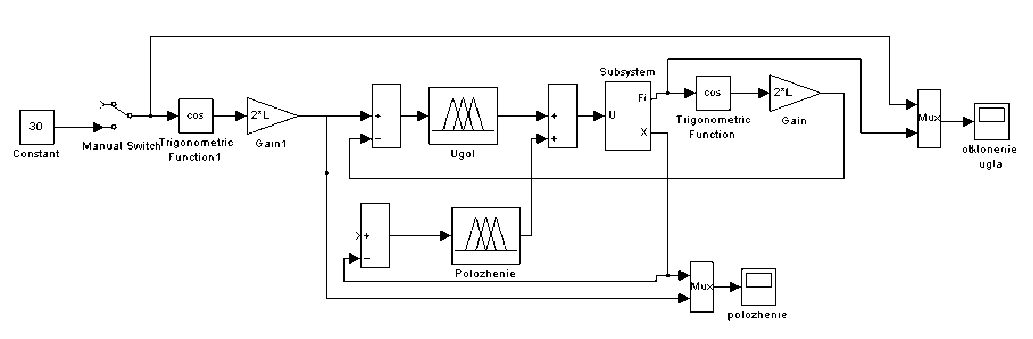
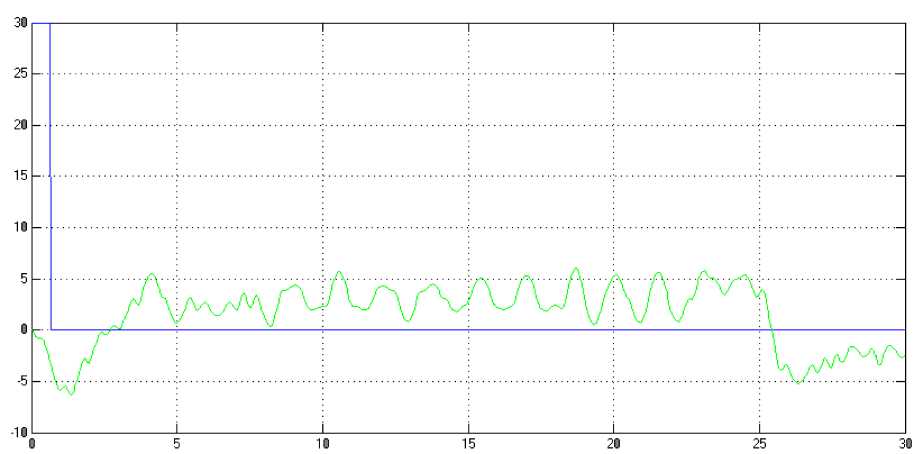
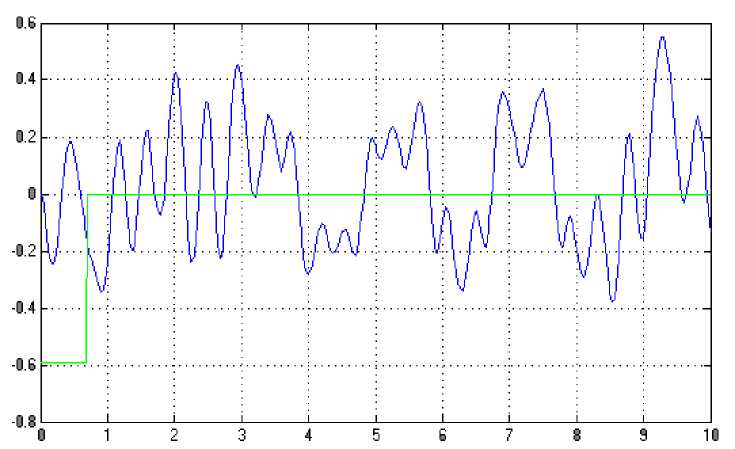
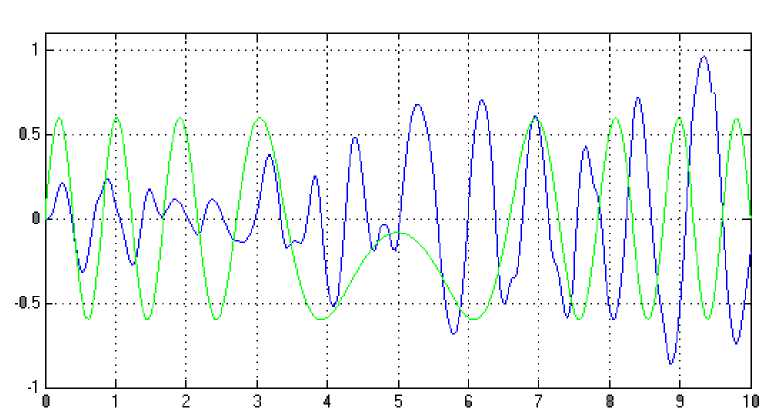
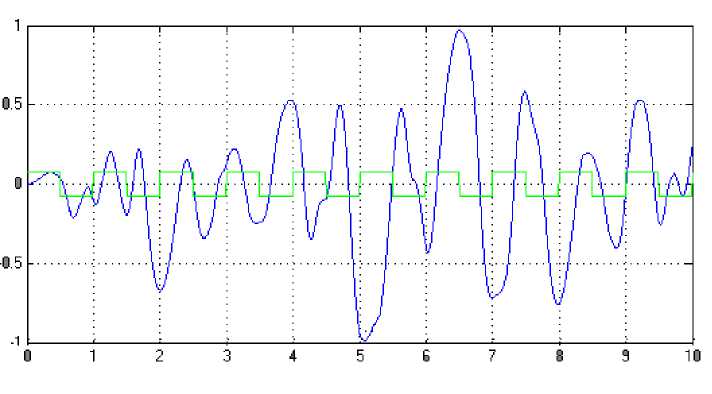
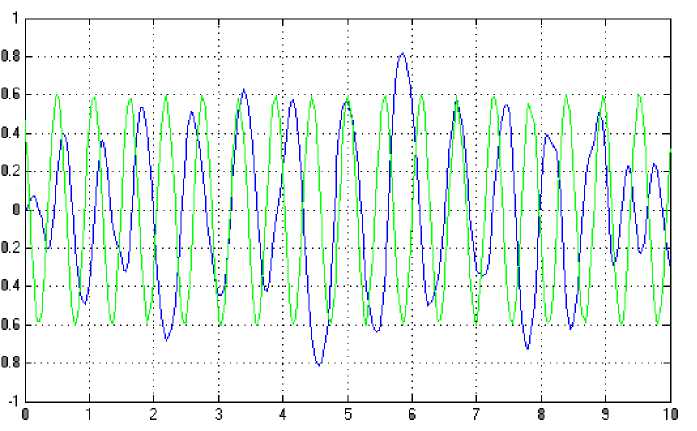
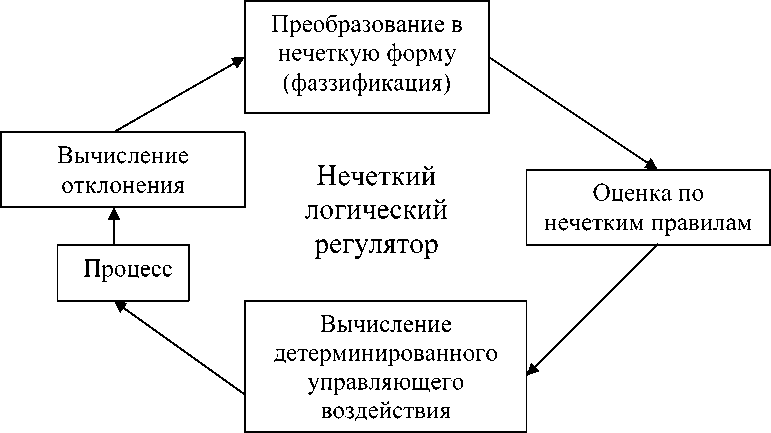
(M + m)x + bx-mLфcos Подставив выражения для H(t) из уравнения (5) и для V(t) из уравнения (6) в уравнение (3), получим: (J + mL2)ф- mLxcosф-mgsin ф .(8) Уравнения (7) и (8) являются нелинейными уравнениями, составляющими математическую модель перевернутого маятника на тележке. Далее исследуем систему на управляемость и наблюдаемость, а также проверим адекватность составленной нами математической модели, проверив систему на устойчивость. На данном этапе воспользуемся классическими методами теории автоматического управления. Исходя из этого необходимо линеаризовать уравнения (7) и (8) и записать их в форме уравнений в переменных состояния. Искомая передаточная функция системы имеет вид: mLp Где w (p) = (p^ =--------5— U(p) 2 , b(J + mL2)p2 r (M + m) mgL bmgL rr r = (M + m)(J + mL2) - m2L2. (14), Уравнения системы в переменных состояния. xi(t) x 2(t ) x 3(t ) x 4(t ) b ( J + mL2) J ( M + m ) + MmLL bmL J ( M + m ) + MmLL m2gL( M + m ) J (M + m ) + MmL2 0 mgL (M + m ) J (M + m ) + MmL2 J + mL2 B J ( M + m ) + MmLL 0 mL J ( M + m ) + MmL2 Поскольку в ходе исследования нас будут интересовать угол поворота маятника относительно вертикали ) и координата тележки x(t), то уравнение выхода запишется в следующем виде: y = Cx + Du (t) , где У(t) = У1(t) . У 2(t )J , C Т.к. порядок числителя передаточной меньше порядка знаменателя, то матрица D : 0 0 0 0 1 0J, функции нашей системы D . Построим отклик системы на импульсное воздействие (импульсную функцию) (рис. 3) и корневой годограф. А Б Рис 3. Импульсная функция (А) и корневой годограф (Б). Как видно из графиков, один полюс системы движется в положительной части комплексной плоскости, и это также говорит о том, что наша система без управления является неустойчивой. Построим график фаззификации, соответствующий функциям принадлежности: Рис. 4. Функции принадлежности входных переменных. Теперь словесно опишем последовательность действий человека, когда он, например, в ручную пытается удержать маятник на тележке в равновесии. Рассуждения выглядят так: а) "быстро" переместить б) "чуть-чуть" переместить тележку в) переместить тележку со "средней тележку в положительную сторону в положительную сторону сокростью" при маленьком при "большом положительном" при "нулевом положительном" отрицательном отклонении отклонении. отклонении Рис. 5. Управление перевернутого маятника человеком. Рис. 6. Функции принадлежности управления. Проведя указанные выше рассуждения, приступаем к непосредственному моделированию нечеткого регулятора. После создания нечеткого регулятора в пакете Fuzzy Logic Toolbox cобираем непосредственно схему моделирования (рис. 7). Рис. 7. Схема моделирования. Подавая различное отклонение угла, получаем следующие результаты моделирования: Рис. 8. Реакция системы на единичное отклонение в 22 градуса. Рис. 9. Реакция системы на гармоническое изменение входного параметра. Рис. 10. Реакция системы на прямоугольное изменение входного параметра. Рис. 11. Реакция системы на стохастическое изменение входного параметра. В процессе моделирования замечено, что стержень не падает, но за несколько десятков секунд тележка маятника теоретически перемещается на несколько метров. Поэтому в систему был введен нечеткий регулятор по положению. При его создании было наложено ограничение на перемещение маятника. Пусть маятник может перемещаться только в пределах двух метров. При отклонении маятника от вертикальной оси, он «отбрасывает» проекцию на горизонтальную ось. В общем случае выражение проекции на горизонтальную ось выглядит следующим образом: lx l sin a . (24) Графически данное выражение можно представить следующим образом: Рис. 12. Пример нахождения проекции на ось ОХ. Т.к. в нашей системе максимальный угол отклонения физически не может превышать 900, а длина маятника 2 L , причем L 0,3 то входная величина может изменяться в интервале [-0.6 0.6]. При вертикальном положении маятника его проекция на ось ОХ равна 0, при горизонтальном положении проекция равна 2 L -, т.е. длине маятника. Если взять регулятор по углу, , и изменить только функции принадлежности входной величины, то получится новый нечеткий регулятор с управлением по проекции маятника на горизонтальную ось. Соберем схему моделирования, состоящую из математической модели самого маятника и двух нечетких регуляторов по углу и по положению (рис. 14). Рис.13. Схема моделирования. Подавая различное отклонение угла, получаем следующие результаты моделирования: Рис. 14. Зависимость выходного значения угла от входа. Рис. 15. Изменение положения координаты тележки. Из графика видно, что за время моделирования тележка перемещалась в пределах интервала [-0.4 0.6], что удовлетворяет введенным нами ограничениям. Приведем перемещение тележки при различных видах входного воздействия. Рис. 16. Перемещение тележки при гармоническом изменении угла. Рис. 17. Перемещение тележки при прямоугольном изменении угла. Рис. 18. Перемещение тележки при пилообразном изменении угла. На основании результатов всех предыдущих пунктов сформулируем алгоритм нечеткого управления объектами типа перевернутый маятник (рис. 19). Рис. 19. Графическое представление алгоритма нечеткого управления объектами типа перевернутый маятник. Определение основных управляющих воздействий состоит из четырех основных этапов: 1. Получение отклонения. 2. Преобразование значения отклонения к нечеткому виду, такому как «большой», «средний» и т. п. 3. Оценка входного значения по заранее сформулированным правилам принятия решения посредством композиционного правила вывода. 4. Вычисление детерминированного выхода, необходимого для регулирования процесса. Данный алгоритм позволяет создать требуемый нечеткий регулятор по определенным заранее входным величинам.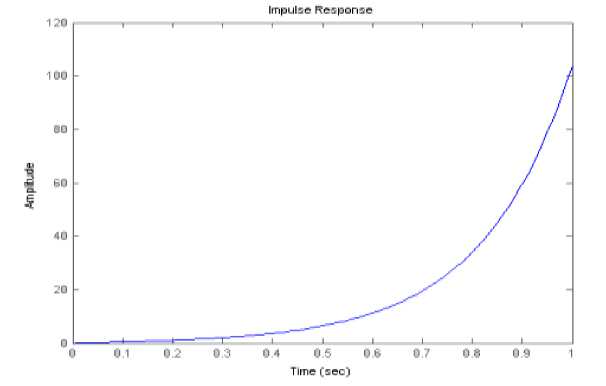
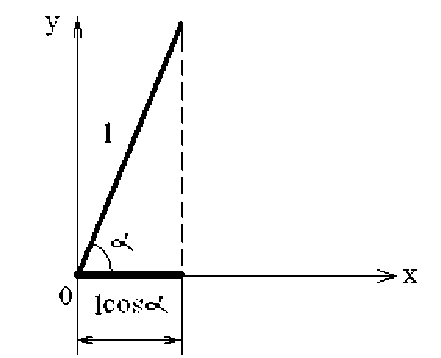
Список литературы Разработка интеллектуального алгоритма управления объектами типа перевернутый маятник
- Деменков Н.П. Нечеткое управление в технических системах. -М.: Издательство МГТУ им Н. Э. Баумана, 2005.
- Певзнер Л.Д., Чураков Е.П. Математические основы теории систем. -М.: Высшая школа, 2009.
- Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. -М.: Горячая линия -Телеком, 2006.
- Штовба С.Д. Проектирование нечетких систем средствами Matlab. -М.: Горячая линия -Телеком, 2007.
- Kevin M. Passino, Stephen Yurkovich. Fuzzy Control, Addison-Wesley, 1998.


