Разработка интерполирующего фильтра с многоканальной архитектурой

Передискретизация в теории цифровой обработки сигналов – процесс изменения частоты дискретизации цифрового сигнала. Алгоритмы передискретизации находят широкое применение при обработке аудиосигналов, радиосигналов и изображений. Отсчеты сигнала, полученного на новой частоте дискретизации, рассчитываются на основе уже имеющихся отчетов и не содержат новую информацию.

Передискретизация

Процесс увеличения частоты дискретизации называют интерполяцией, процесс понижения – децимацией.

В соответствии с теоремой Котельникова любой непрерывный сигнал со спектром, ограниченным сверху некой частотой Fn, может быть представлен как набор отсчетов дискретного сигнала с частотой дискретизации Fs ≥ 2 ∗ Fn(т.е. максимальная частота сигнала должна быть минимум вдвое меньше, чем частота дискретизации). Подобное представление является взаимно однозначным, т.е. при соблюдении вышеупомянутого условия любой дискретный сигнал можно представить в виде непрерывного сигнала с ограниченным спектром без искажений.

При проведении дискретизации отсчеты сигнала, взятого с частотой дискретизации FS1, вычисляются на основе известных отсчетов сигнала, взятого с частотой дискретизации FS2 . При этом выполняется условие теоремы Котельникова, т.е. при максимальной частоте спектральной составляющей сигнала Fn имеет место выражение FS1 ≥ 2 ∗ Fn, FS2 ≥ 2 ∗ FS2 . Таким образом, можно рассматривать передискретизацию как последовательность восстановления дискретного сигнала с частотой дискретизации FS1 в непрерывный сигнал с ограниченным спектром и дискретизацию этого непрерывного сигнала с частотой FS2 .

Математически интерполяция осуществляется с помощью цифровых фильтров, при этом выражение для неё принимает следующий вид:

y(t) = ∑x(ti) ∗ h(t - ti), где h(t) — импульсная характеристика соответствующего восстанавливающего фильтра, yi – выходной отчет фильтра, xi - входной отчет фильтра. Вид этого фильтра выбирается в зависимости от задачи.

Для общего случая данные вычисления являются затруднительными.

Тем не менее, существуют частные случаи передискретизации, для которых процесс получения новых отсчетов требует малого количества вычислений:

• •    децимация с целым коэффициентом, т.е. уменьшение частоты дискретизации в целое число раз;

• •    интерполяция с целым коэффициентом, т.е. увеличение частоты дискретизации в целое число раз;

• •    передискретизация в M/N раз.

Последний случай можно рассматривать как линейную комбинацию двух первых случаев передискретизации.

Типичный алгоритм интерполяции сигнала с целым коэффициентом (FS1 – старая частота дискретизации, FS2 = FS1 ∗ N – новая частота дискретизации, N – коэффициент передискретизации) выглядит так:

• 1.    В отсчеты сигнала с частотой сигнала F_S1 производится вставка нулевых отсчетов. Между каждыми двумя отсчетами вставляется

• 2.    Полученный сигнал фильтруется цифровым фильтром нижних частот. Поскольку цифровой спектр повторяется спустя F_S1 Гц, при увеличении частоты дискретизации в спектре сигнала появляются зеркальные спектральные составляющие;

• 3.    Поскольку до передискретизации и после мощность сигнала сохраняется, а количество отсчетов увеличивается в N раз, необходимо умножить выход фильтра аналогично в N раз для сохранения амплитуды сигнала. В качества альтернативы можно сразу умножить коэффициенты фильтра нижних частот в N раз.

N - 1 нулей. С этого момента происходит увеличение частоты дискретизации;

Структурно данная процедура изображена на Рис. Х. Сверху изображен сигнал в частотной области, снизу во временной области. На первой части изображен сигнал с частотой дискретизации FS1 = 800 МГц, на второй происходит вставка нуля между каждыми двумя отсчетами, при этом частота дискретизации меняется на FS2 = FS1 ∗ N = 800 МГц ∗ 2 = 1600 МГц. На третьей части рисунка происходит фильтрация сигнала от частотный составляющих.

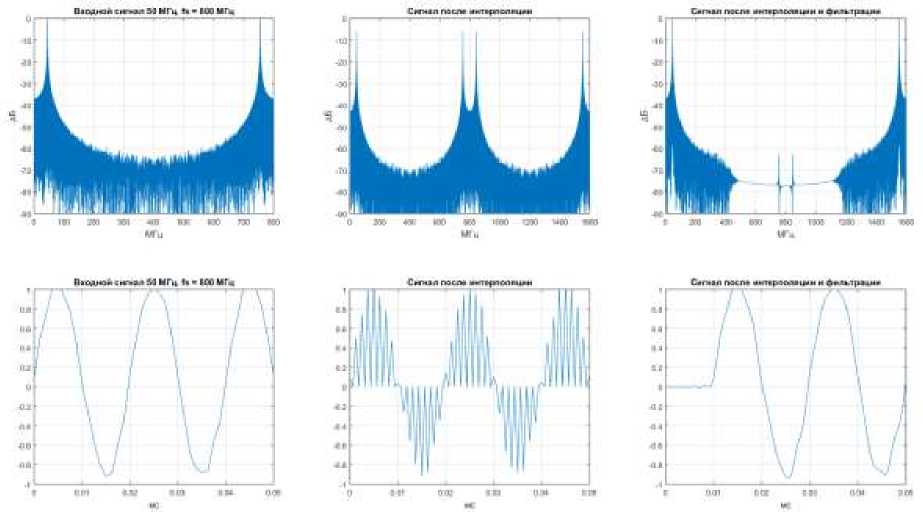
Рисунок 1. Интерполяция синусоидального сигнала

При программной реализации интерполяции нулевые отсчёты не участвуют в вычислении выходного сигнала фильтра, что позволяет оптимизировать процесс вычисления. При аппаратной реализации для экономии ресурсов возможно использование полифазных фильтров.

Проектирование фильтра-интерполятора

Рассмотрим простой пример реализации FIR фильтров. Как известно, существует два больших класса фильтров — БИХ, с бесконечной импульсной характеристикой и КИХ, с конечной импульсной характеристикой. Остановимся на втором типе: КИХ фильтрах (англ. FIR — «finite impulse response»). КИХ фильтр — это линейный цифровой фильтр, основной особенностью которого является ограниченность во времени его импульсной характеристики, то есть с определенного момента времени она становится равной нулю. Как правило, большинство КИХ фильтров выполнено без обратной связи, поэтому практически все КИХ фильтры — нерекурсивные.

На Рис. 2 представлена реализация КИХ фильтра в общем виде.

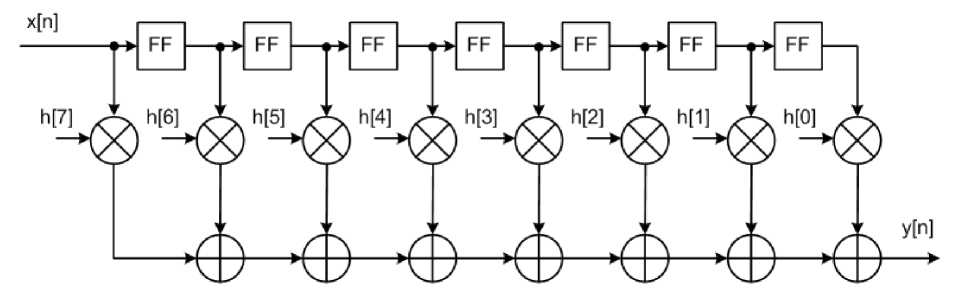
Рисунок 2. Структура КИХ-фильтра

В случае реализации фильтра с многоканальной архитектурой структурная схема значительно усложняется. При двух входных каналах и четырех выходных получается следующая структура:

• •    Два сдвиговых регистра для каждого из каналов;

• •    Четыре мини-фильтра, каждый из которых вычисляет выходное значение для каждого из выходных каналов.

Изначальная частота дискретизации равна тактовой частоте, умноженной на 2, новая частота дискретизации равна тактовой частоте, умноженной на 4.

Существует полифазная структура фильтра, позволяющая рассчитывать выходные отсчеты на низкой частоте дискретизации за счет разделения фильтров на несколько составляющих и дальнейшее переключение между ними с помощью выходного мультиплексора, чья тактовая частота равна новой частоте дискретизации.

Основное отличие полифазного фильтра от многоканального состоит в разном принципе разделения основного фильтра на мини-фильтры. При полифазной реализации каждый коэффициент входит в один из минифильтров всего один раз, в то время как в многофазной реализации в каждом из мини-фильтров присутствует ровно половина всех коэффициентов. Таким образом, методика построения многоканального фильтра является нетривиальной задачей.

Все КИХ-фильтры описываются следующими уравнениями:

y(n) = / h(k)x(ji — /с) k=o

N-l H^z) = h(k')z~k k = 0

где y(n) — выходной сигнал (функция текущего и прошедших значений на входе), x(n) — входное воздействие, h(k) — коэффициенты импульсной характеристики, N — длина фильтра (количество коэффициентов фильтра), H(z) — передаточная характеристика фильтра.

Самая важная особенность КИХ фильтров заключается в возможности получения точной линейной фазовой характеристики. Остановимся на этом моменте подробнее. Сигнал подвергается различным преобразованиям при прохождении через фильтр. В частности, изменяются амплитуда и фаза сигнала в зависимости от частотной характеристики фильтра (амплитудной, АЧХ и фазовой, ФЧХ). Для многочастотных сигналов недопустимо, чтобы при прохождении блоков обработки, фаза сигнала искажалась. Причем, если АЧХ в полосе пропускания сделать практически постоянной не составляет труда, то с ФЧХ возникают проблемы. Для оценки искажений фазы удобно ввести понятия фазовой и групповой задержек.

Фазовая задержка — это величина задержки для каждой из частотных компонент сигнала. Определяется как угол сдвига фазы, деленный на частоту. Групповая задержка — это средняя временная задержка всего многочастотного сигнала. Определяется как производная фазы по частоте. Математически фазовая и групповая задержки записываются следующим образом:

Tph = -6 (co)/соTg = — d6 (a)) / doo

Из формулы для групповой задержки становится очевидно условие линейности ФЧХ фильтра. Если ФЧХ — линейна, то групповая задержка после взятия производной равна константе, то есть постоянна для всех частотных компонент. Логично, что фильтр с нелинейной ФЧХ будет вносить искажения в фазу сигнала.

Таким образом, линейность фазовой характеристики — одна из важнейших особенностей КИХ-фильтров. Остановимся на изучении этого класса фильтров.

Проектирование КИХ фильтров

Под «расчетом FIR фильтра» в большинстве случаев понимают поиск его коэффициентов по значениям частотной характеристики.

При создании нового цифрового КИХ фильтра любой инженер проходит через определенные стадии разработки*:

• •    Спецификация фильтра. Задается тип фильтра (ФНЧ, ФВЧ, полосовой, режекторный), количество коэффициентов N, требуемая частотная характеристика, с допусками на нелинейность в полосе затухания и полосе пропускания и т. д.

• •    Вычисление коэффициентов. Любыми доступными способами и средствами вычисляются коэффициенты фильтра, удовлетворяющие спецификации из предыдущего пункта.

• •    Анализ следствий конечной разрядности. На этом этапе оценивается влияние эффектов квантования на коэффициенты фильтра, промежуточные и выходные данные.

• •    Реализация. На этой стадии происходит разработка фильтра на доступном языке программирования или реализация фильтра путем создания готовых IP-ядер.

* — этапы разработки могут быть несколько иными, но суть всегда остается та же.

Спецификация фильтра

На этой стадии производится поиск компромиссных решений для реализации требуемого фильтра с нужными параметрами. Их немного, но часто приходится жертвовать одним параметром для достижения требуемых значений по другим величинам.

Apass — неравномерность в полосе пропускания, дБ;

• •   Astop — уровень затухания в полосе подавления, дБ;

• •    Fpass — граничная частота полосы пропускания, МГц;

• •    Fstop — граничная частота полосы затухания, МГц;

• •    N — порядок фильтра (количество коэффициентов фильтра).

Значение Apass должно быть как можно меньше, Apass как можно больше, а отношение Fpass/Fstop в идеале стремится к единице (идеально прямоугольная АЧХ). Количество коэффициентов не зря вносится в спецификацию фильтра. Как будет показано далее, от порядка фильтра N и разрядности коэффициентов зависят параметры частотной характеристики фильтра, а также объем занимаемых ресурсов на ПЛИС или СБИС.

Предъявляемые к разрабатываемому фильтру-интерполятору требования:

• •   Apass — 0.01 дБ,

• •   Astop — 64 дБ,

• • Fpass — 300 МГц,

• •    Fstop — 500 МГц,

• •    N — не более 36.

Вычисление коэффициентов фильтра

В математическом пакете Octave было разработано несколько вариантов фильтра-интерполятора, в том числе с использованием оконного метода. В Табл. 1 представлена сравнительная характеристика разработанных фильтров, в том числе с помощью оконных методов.

Таблица 1. Сравнительная характеристика разработанных фильтров.

Методы синтеза фильтра
	Количество коэффициентов	Уровень подавления, дБ	Размер переходной полосы, МГц	Неравномерность в полосе пропускания, дБ
Желаемые показатели	Не более 36	Не менее 62 дБ	От 300 МГц до 500 МГц	Не более 0.001 дБ
Оконный метод Хэннинга	38	72	320 – 510	0.00058
Оконный метод Кайзера	36	68	280 – 430	0.0002
Метод частотной выборки	32	56	290 – 350	0.015
Метод наименьших квадратов	36	67	300 – 500	0.003
Метод равномерных биений	32	64	320 – 500	0.0006

Прямая и обратная каноническая форма фильтра

Существуют две формы реализации фильтра, так называемая прямая и обратная каноническая форма, изображенные на Рис. 3. Как видно по формуле, оба этих фильтра реализуют одну и ту же функцию.

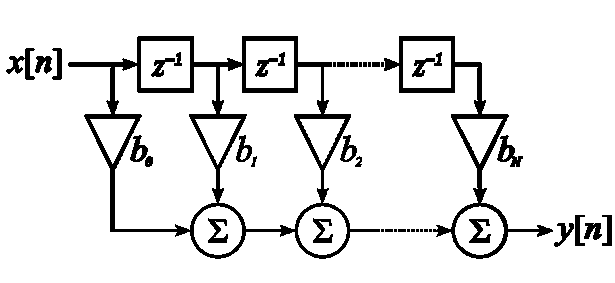
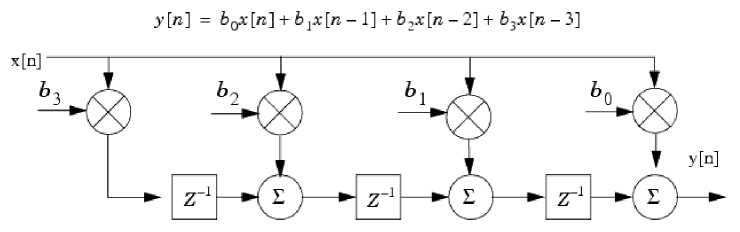
Рисунок 3. Прямая и обратная каноническая форма фильтра

В то время как прямая форма фильтра предлагает использовать отдельный умножитель для каждого коэффициента, обратная форма позволяет использовать некий комбинированный умножитель с несколькими выходами, что возможно благодаря тому, что во всех умножениях используется один и тот же операнд – входной отсчет. Для сравнения была использована библиотека TSMC 90 LP, синтез производился с использованием средства Synopsys Design Compiler. Результаты синтеза отображены в Табл. 2.

Таблица 2. Сравнение площади и потребления

Сравнение площади и потребления
	Фильтр с линиями задержки	Фильтр без умножителей
Мощность, mW	4.6034	5.3110
Площадь, мкм	35994	48470

Основываясь на Табл. 2, можно сделать вывод, что фильтр с линиями задержки имеет преимущество и по мощности, и по площади. Стоит заметить, что оба фильтра работают с одинаковой тактовой частотой 400 МГц, и оба фильтра укладываются в тайминг.

Вывод

В данной статье была рассмотрена интерполяция цифрового сигнала и архитектуры фильтров-интерполяторов. Были разработаны различные варианты фильтров, отличающиеся методикой расчета. После выбора наиболее подходящего под спецификации фильтра было рассмотрено две формы фильтра – прямая и обратная каноническая, и после синтеза средствами Synopsys Design Compiler была выбрана форма фильтра, имеющая меньшее потребление и меньшую площадь.