Разработка комбинированной модели ARIMA для прогнозирования спроса на продукцию металлургической отрасли

В настоящее время на предприятиях металлургической отрасли особую актуальность принимает процесс прогнозирования спроса на производимую продукцию [2, c. 35-37]. Исследование и прогнозирование спроса позволяет выработать ассортимент предлагаемых товаров так, чтобы обеспечить максимальную прибыльность деятельности и превзойти конкурентов [3, с. 73-82].

Целью данного исследования является разработка модели прогнозирования с помощью методики Бокса-Дженкинса, а также прогнозирования спроса на ближайший год.

Приступая к построению модели прогнозирования, рассмотрим исходные данные, эмпирическую и инструментальную базы исследования:

• •    временные ряды динамики спроса на продукцию металлургической отрасли (за 2015-2018 года);

• •    методика Бокса-Дженкинса построения ARIMA – моделей;

• •    программно-аппаратный модуль IBM SPSS для практической реализации процесса прогнозирования.

Все работы были проведены в программно-аппаратном модуле IBM SPSS, который позволяет автоматизировать расчетные операции процесса. По умолчанию для всех моделей был принят уровень значимости α = 0,05.

Для построения прогноза с помощью модели ARIMA были выбраны типы продуктов, для которых используемая модель не даёт достаточно точные результаты.

Для каждого временного ряда будет создана модель по методу ARIMA, экспериментальным способом (опираясь на результаты предварительного исследования) к ней были подобраны два набора (сезонных и несезонных) параметров p (авторегрессия), r (порядок интегрирования) и q (скользящее среднее).

Разработанные комбинированные модели ARIMA авторегрессии и скользящей средней с учетом сезонной компоненты имеют общий вид [1, с. 156]:

Vt = (« 1 + P 1 * y_t - 1 + P 2 * y_t - 2 + - + P k * y_t - k )

+ ⁽Et -41* E t- 1 + q₂ * E t-2 + - + kk * E t-k )

+ ⁽£ 1 + P 5 1 * У t -1 + P 5 2 * У _t - 2 + - + P kk* У t - k )

+ (E t — k 51 * E t-1 + q 52 * E t-2 + - + kSk * E t-k)

где y_t – прогнозируемое значение функции Y в момент времени t ;

y_t__T ,…, y_t—k – значение функции Y в момент времени t-k ;

s_t ,…, E_t-k – уровень «белого шума» в момент времени t ;

«! , ^1 – несезонная и сезонная константы;

Pl,…, Pk ; P^S1 ,…, PSk – несезонные и сезонные параметры авторегрессии;

Qi,…, 4k ; qs_T ,…, qSk – несезонные и сезонные параметры скользящей средней.

Проведём предварительный анализ динамики спроса на коммерческую оцинковку (рис.1).

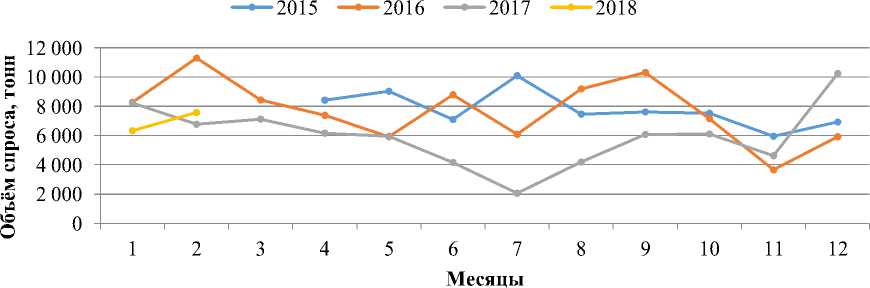
Рис. 1. Динамика объёмов спроса на коммерческий оцинкованный прокат

Анализируя график можно сделать вывод, что спрос на коммерческую оцинковку является сезонным. Наибольшие объёмы спроса – в январе, декабре и феврале, самые низкие – в июне, июле, августе.

Летом всплеск объясняется «оживлением» строительного рынка. В свою очередь зимой происходит падение цен и клиентам выгодно покупать металл на склад, при этом им необходимо компенсировать стоимость хранения.

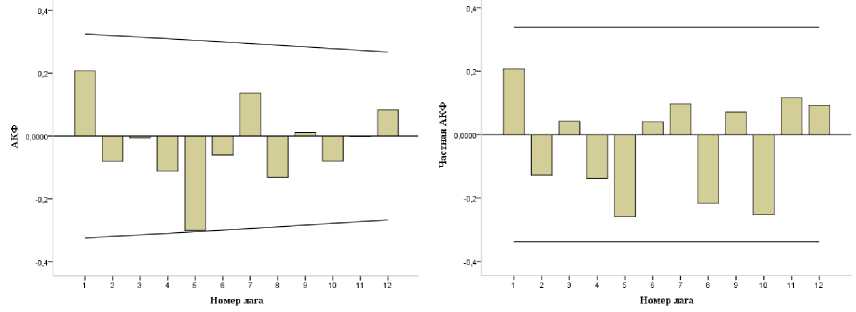
На основании данных лаговой переменной строим ЧАКФ (частная авто- корреляционная функция), которая послужит нам иллюстрацией регрессионной зависимости между показателями в одинаковые периоды (месяцы) разных лет и даст возможность экспертным методом определить значение коэффициента регрессии для итоговой модели. АКФ (автокорреляционная функция) и ЧАКФ по лаговой переменной представлены на рисунке 2 (на рисунках столбцами обозначены коэффициенты автокорреляции, а линиями обозначены верхний и нижний доверительные интервалы).

(а)                                         (б)

Рис. 2. Автокорреляционная (а) и частная автокорреляционная (б) функции для коммерческого оцинкованного проката

Анализируя графики функций можно сделать вывод о наличии достаточно высокого значении коэффициента регрессии между данными некоторых месяцев. Следует отметить, что временной ряд является стационарным. Варианты подбора параметров и полученные зна- чения коэффициентов представлены в табл.1 (были выбраны наиболее хорошие результаты). Далее проведём анализ полученных значений и выберем модель, которая даёт наилучшие значения по исследуемым параметрам.

Таблица 1. Набор параметров модели ARIMA для коммерческого оцинкованного проката

Модель	Значение параметра
	R-квадрат	Скорректированный R-квадрат	MAPE, %
ARIMA (3, 0, 1) (1, 0, 1)	0,49	0,325	23
ARIMA (2, 0, 1) (1, 0, 1)	0,683	0,412	18
ARIMA (2, 1, 1) (1, 0, 1)	0,323	0,223	45

Анализируя данные параметров видно, что наилучшие показатели для модели ARIMA (2, 0, 1) (1, 0, 1). Следует отметить, что точность прогнозирования выбранной модели составляет 82%.

Окончательный вариант модели прогнозирования спроса на коммерческую оцинковку имеет следующий вид:

yt=(33128,26+0,55∗yt_i-0,32∗yt_2)+(Et+0,42∗st-l) + (1773,64 +(El -0,91∗Et-1)․

-

0,96 ∗ Ус-i)

Произведём сравнение прогнозных и реальных значений за февраль, март и апрель, показатели данных периодов не

учитывались при составлении прогноза (рис. 3).

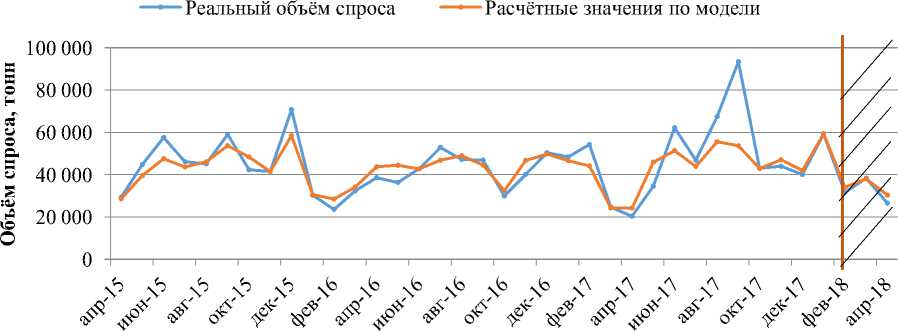
Рис. 3. Сравнение прогнозных и реальных объёмов спроса на коммерческий оцинкованный прокат

Пробный прогноз по модели ARIMA даёт положительные результаты. На февраль прогнозный объём спроса превышает реальный на 7%. В марте прогнозное значение меньше реального на

0,6%. В апреле значение данного показателя выше на 14%.

Прогноз спроса с февраля 2018 по март 2019 представлены на рис.4.

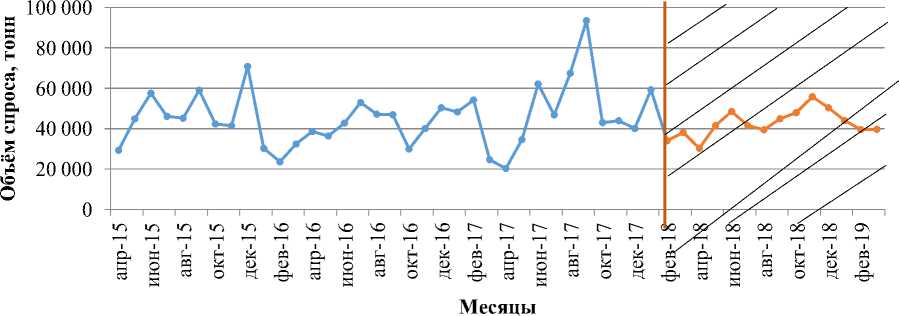
Рис. 4. Прогноз спроса на коммерческий оцинкованный прокат с февраля 2018 по февраль 2019 года

Анализируя результаты прогнозирования можно сделать вывод росте динамики спроса в августе-декабре 2018 года и о снижении в январе-феврале 2019 года.

Следует отметить, что точность прогнозирование модели составляет 82%, что говорит о достаточно высокой точности и возможности применения в процессе планирования разработанной модели.