Разработка концепции обобщенной нейронносетевой модели

Основное назначение искусственных нейронных сетей (ИНС) – имитация функций человеческого мозга [1], а именно: памяти, распознавания информации и ее предсказывание. Каждая нейронносетевая модель, вследствие особенностей ее обучения и функционирования, направлена на решение конкретных задач.

Данное обстоятельство является главным фактором, препятствующим созданию имитационных математических моделей (ИММ) с использованием ИНС как структурного элемента.

Создание подобных систем позволит объединить свойства входящих в них ИНС, обобщая алгоритм обработки входящей информации, и обеспечит адекватное реагирование на входящие сигналы из окружающей среды.

РАЗРАБОТКА КОНЦЕПЦИИ ОБОБЩЕННОЙ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ

Основой построения ИНС служит формальный нейрон [2], представляющий собой сумматор входных сигналов X, умноженных на вес нейрона W, передаваемых в функцию активации нейрона F и выдаваемого результирующего сигнала Y (рис. 1).

Обучением ИНС служит настройка весов ее нейронов таким образом, чтобы при прохождении входных сигналов получить желаемый результат. В противном случае алгоритм обратно-

Иванов Максим Викторович, аспирант кафедры И2 “Инжиниринг и менеджмент качества”.

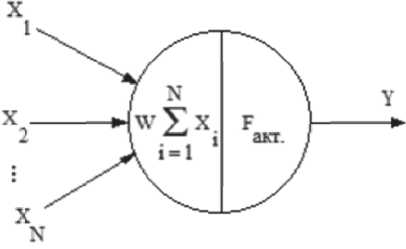
Рис. 1. Формальный нейрон го распространения ошибки меняет вес нейрона на величину разницы между желаемым и реальным выходными сигналами нейрона [3].

Рассмотрим ИММ со структурой, представленной на рисунке 2.

Структурными элементами данной ИММ являются ИНС, конфигурации которых представлены на рисунке 3.

В узком смысле ИНС-элементы системы - самостоятельные подсистемы, обученные выдавать конкретные решения в ответ на диапазон подаваемых в систему сигналов. В случае принятия ИНС-элементами незнакомого сигнала, они выдают результат, максимально близкий к их внутреннему представлению [4]. В широком смысле ИНС-элемент – это нелинейный преобразовательный элемент, нелинейность которого обеспечивается входящими в его нейроны функциями активаций [5].

Чтобы моделируемая система могла адекватно реагировать на входящие сигналы из внешней среды, необходимо, чтобы имелась обратная связь результирующих сигналов с входящими [6]. Подобный механизм реализован

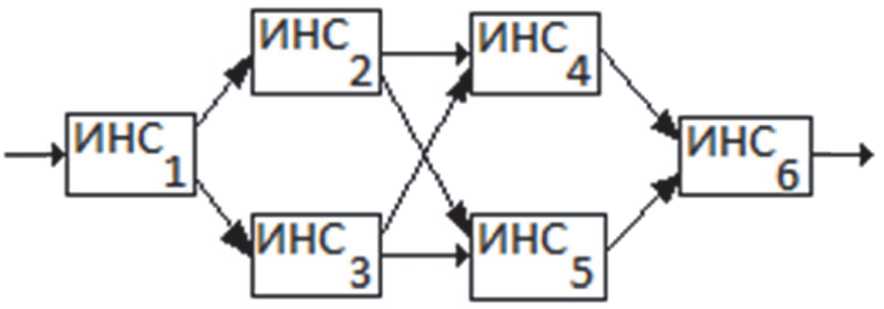
Рис. 2. Имитационная математическая модель со структурными элементами в виде искусственных нейронных сетей

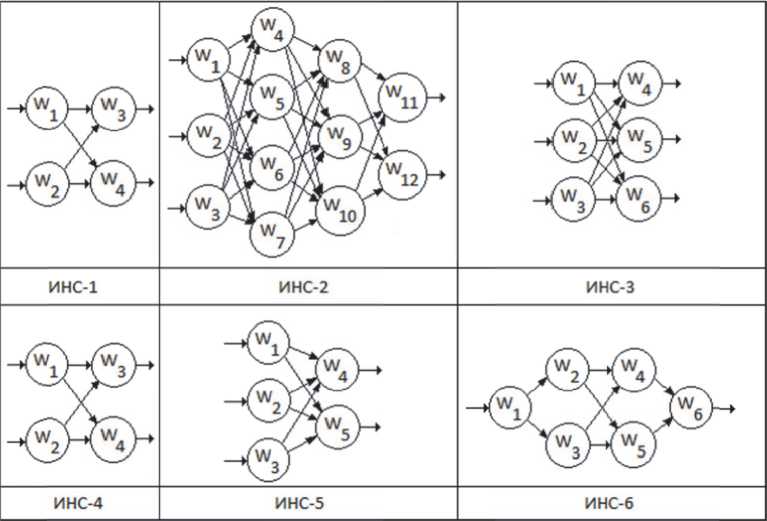
Рис. 3. Конфигурации искусственных нейронных сетей, входящих в имитационную математическую модель

в большинстве современных алгоритмов обучения ИНС [7], следовательно, целесообразно представлять рассматриваемую систему в виде ИНС, при этом, ее элементы будут также являться ИНС. Данную концепцию в дальнейшем будем называть обобщенной ИНС (ОИНС). В то время как ИНС решает конкретные задачи, на которые обучена, ОИНС в перспективе способна решать комплекс задач, определяемый набором ИНС, входящих в ОИНС. Для создания ОИНС необходимо сформулировать ряд принципов построения и правил распространения и обработки сигналов.

ИНС, как таковая, не обладает собственными весовыми характеристиками, необходимыми для функционирования внешней системы, как ОИНС. Следовательно, необходимо «наделить» ее такой характеристикой. Каким образом может быть получен вес ИНС?

Во внешнюю среду из ИНС выходят результаты Y обработки входных сигналов X. Поскольку ИНС представляет собой отдельный структурный элемент ОИНС, то полученный выходной сигнал из ИНС возможно представить как ее вес (рис.4). В дальнейшем сигналы, распространяемые внутри ОИНС будем обозначать как Z, а результирующий сигнал ОИНС - как Z0.

Очевидно, что для получения выходного сигнала Z внутри ОИНС или Z0 на выходе из ОИНС, необходимо обработать входные сигналы X или входящие сигналы Z соответственно с помощью внутренней ИНС, а затем повторно их обработать по алгоритму функционирования искусственного нейрона (рис. 5).

Руководствуясь данными положениями, представим рассматриваемую ИММ в виде ОИНС (рис. 6).

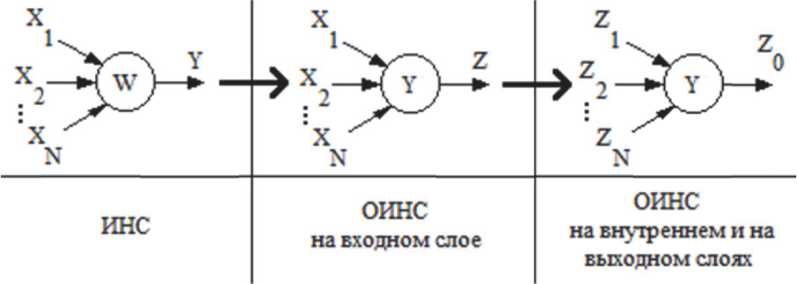
Рис. 4. Представление выходного сигнала ИНС как веса в масштабе ОИНС

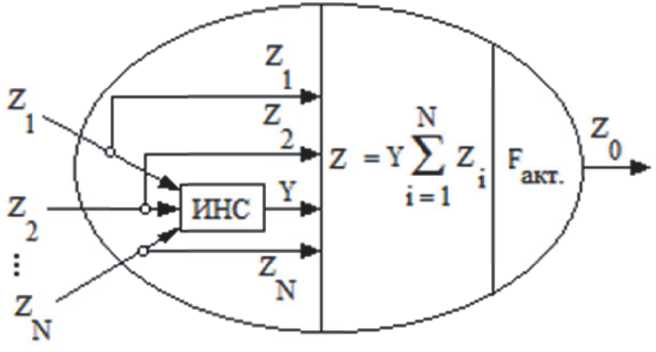
Рис. 5. Обработка сигналов элементом ОИНС

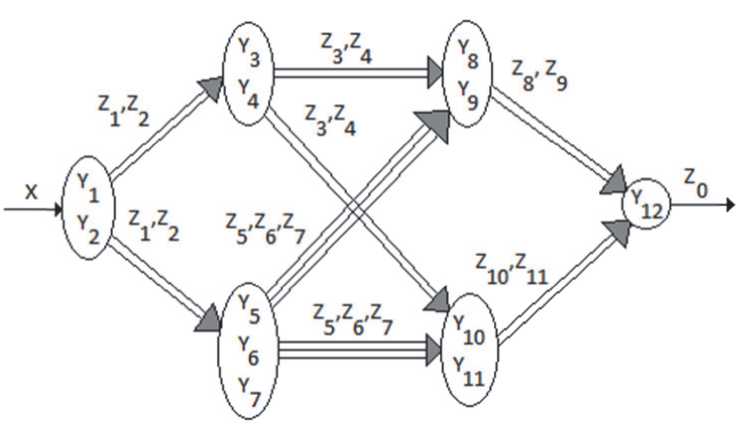
Рис. 6. ОИНС, содержащая несколько весов в каждом структурном элементе

Так как в рассматриваемых моделях ИНС присутствуют два и более выходных сигналов, то в полученной ОИНС имеются элементы с несколькими весовыми характеристиками, что противоречит теории ИНС, утверждающей, что искусственный нейрон может иметь только один весовой коэффициент. Руководствуясь данным принципом, приведем ОИНС к виду стандартной ИНС, в которой каждый вес пред- ставляет собой нейрон, содержащий в себе ту модель ИНС, из которой он был получен (рис. 7).

Таким образом, мы получаем двухуровневую нейронную сеть, пригодную для реализации любыми доступными на сегодняшний день инструментами по созданию ИНС-моделей.

Достоинством полученной модели является решение комплекса задач ОИНС, определяемого набором входящих в нее ИНС. При специфи-

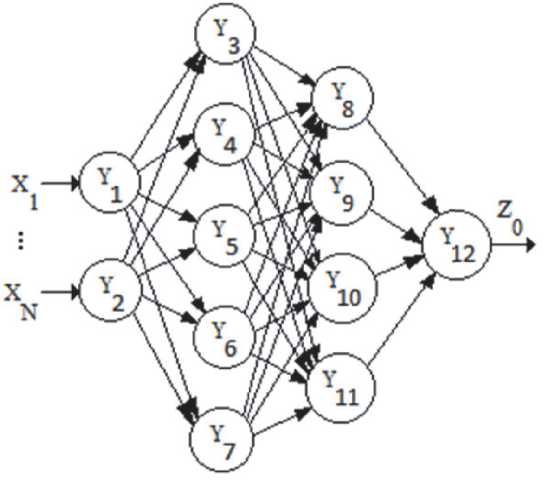
Рис. 7. ОИНС, приведенная к стандартному виду ИНС

ческом обучении ОИНС круг решаемых задач возможно расширить.

Существенным недостатком ОИНС является 5 значительное снижение ее быстродействия по сравнению с ИНС, вследствие последовательной многоуровневой обработки входящих в систему 6 сигналов.

ВЫВОДЫ

. Рассмотрена имитационная математическая модель, содержащая искусственные нейронные сети как отдельные элементы.

. Выявлены недостаток рассматриваемой модели в задачах построения адаптирующихся систем, а именно: узкий круг решаемых задач 1. входящими в систему искусственными нейронными сетями.

. Сформулированы правила и принципы построения обобщенных нейронных сетей, ре- ^2. шающих проблему построения адаптирующихся систем, содержащих искусственные нейронные сети в качестве структурных элементов.      3.