Разработка математических моделей динамики и оценки усталостной прочности лопаток турбомашин с учетом геометрической нелинейности

Известно, что лопатки турбомашин работают в тяжелых условиях, подвергаясь действию не только переменных аэродинамических нагрузок, но и высокой температуры и большой скорости вращения. Под влиянием этих факторов свойства материала и жесткость конструкции лопаток изменяются. Это приводит к изменениям начальных характеристик работы лопаток. Кроме этого, под действием переменных термомеханических нагрузок лопатки турбомашин часто разрушаются по усталостным причинам. В связи с этим разработка математических моделей для решения задач динамики и оценки долговечности лопаток турбомашин с учетом изменения жесткости конструкции лопаток от температуры и скорости вращения в соответствии с реальными условиями работы, а также обеспечение надежности работы лопаток турбомашин является актуальной проблемой.

В разработанной математической модели влияние температуры и скорости вращения на характеристики работы лопаток турбомашин учтено изменением параметров упругости материала в соответствии с температурой и изменением жесткости конструкции. Для учета изменения жесткости конструкции вследствие температуры и скорости вращения считается, что напряжения от температуры играют роль начальных напряжений конструкции и поэтому в общей матрице жесткости добавлена матрица геометрической жесткости [ K_G ], обусловленная этими начальными напряжениями. При этом уравнение колебания лопаток

турбомашин с учетом геометрической нелинейности имеет вид

ii i

[ M ] { 5 } + [ C № + ( [ K ] + [ K g D{⁵ } = { ^f ( t ) } , (1) где [ M ], [ C ] и [ K ] – матрицы масс, демпфирования и жесткости соответственно; { F } – вектор внешней

i ii узловой нагрузки; {5}, {5} и {5} - векторы узловых

перемещений, скоростей и ускорений ансамбля конечных элементов.

Матрица геометрической жесткости выражается как [1; 2]

[ K g ] = J [ G T ][ 5 ][ G ] dV ,            (2)

V где матрицы [S], [G] определяются следующими уравнениями для трехмерных и двухмерных элементов соответственно:

[ 5 ] =

[ G ] =

^ Xx [ 1 3 ]

4 [ 1 3 ]

^ z [ 1 3 ]

[ 1 3 ] - [ 1 3 ]

^[ 1 3 ] ^ 0 , [ 1 3 ]

4 [ 1 3 ] < [ 1 3 ]

[ 1 3 ] г d x

[ 1 3 ] '

d ,

[ 1 з ] I"

8 z J

[ N ];

[ 1 3 ] =

а Г д 1 0 0 [ 5 ] = ст xx 0 ст yx 0 ;[ Gz ] = 5x 5 [ Nb ], (4) xy yy J — дy где ст0,ст0ст0,ст0,ст0,ст0 - напряжения от темпе-xx yy zz xy yz zx ратуры и вращения. Они определены с помощью статического уравнения

[ ст ⁰] = [ D ]([ B ]{ 5 } - { 8 0 })              (5)

и известного уравнения напряжения

[K]{ 5 } = { F t } + { F },             (6)

где { F T },{ F _n }- векторы температурных и центробежных нагрузок. Векторы и матрицы { F T },{ F }, { 8 ₀},[ N ],[ N b ],[ D ],[ B ] подробно описаны в работах [1; 2].

В качестве объекта изучения рассмотрена реальная рабочая лопатка газовой турбины [1] (рис. 1). Конечно-элементная модель (КЭМ) на основе треугольных оболочечных элементов STIO18 c шестью степенями свободы в узле [1] представлена на рис. 2.

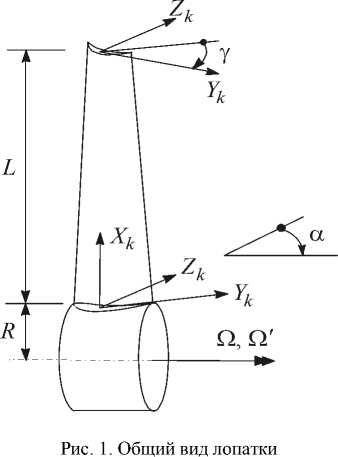
Проведен расчет модели лопатки со следующими характеристиками: длина – 0,328 м; хорда – 0,028 м. Лопатка изготовлена из стали 15X12BНМФ, которая имеет модуль Юнга – 2.16 105 Мпа; коэффициент Пуассона – 0,3; плотность – 7,85 103 кг/м3. Величины коэффициентов демпфирования для первых трех из-гибных форм и двух вариантов демпфирования LOW и HIGH показаны в табл. 1 [1]. Изменения температуры по хорде и высоте лопатки приближены к таковым в реальных условиях [3]: вдоль хорды профиля изменения температуры подчиняются квадратичному закону, по высоте лопатки температура постоянная (рис. 3).

Таблица 1

Коэффициенты демпфирования

Режимы	Коэффициенты демпфирования ζ
	Форма 1	Форма 2	Форма 3
LOW	0,000 75	0,000 94	0,001 1
HIGH	0,001 50	0,001 90	0,002 3

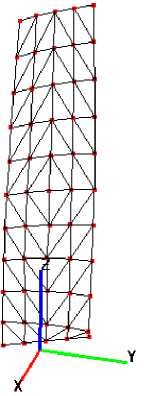
Рис. 2. Конечно-элементная модель лопатки

Были исследованы собственные и вынужденные колебания указанной лопатки. Рассчитаны формы колебаний лопатки (рис. 4). Изменения напряжений по времени в опасной точке показаны на рис. 5. Из этих данных видно, что результаты расчета (рис. 5, а ) и эксперимента (рис. 5, б [4]) практически совпадают. Это подтверждает достоверность разработанных алгоритмов и программ.

На основе результатов расчета изменения напряжений по времени с помощью техники схематизации случайных процессов нагружения (метод «дождя») и кривой усталости по гипотезе Corten–Dolan [1; 5] определена усталостная прочность лопатки. Результаты расчета долговечности лопатки турбомашины в двух случаях демпфирования (HIGH и LOW) без учета температуры показаны в табл. 2.

Таблица 2 Результаты расчета долговечности лопатки турбомашины в двух случаях демпфировании HIGH и LOW без влияния температуры

Режимы	Долговечность (число циклов)
Демпфирование LOW	0,992 7 E + 08
Демпфирование HIGH	0,854 1 E + 09

Видно, что число циклов до разрушения лопатки при демпфировании HIGH (0,854 1 E + 09) больше в сравнении с числом циклов при демпфировании LOW (0,992 7 E + 08).

Было исследовано влияние температуры и центробежных нагрузок на динамические характеристики и долговечность лопатки (табл. 3–5).

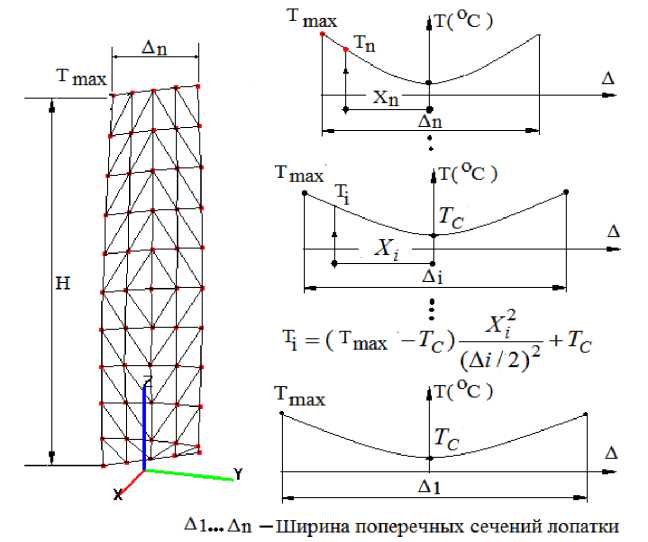
Рис. 3. Закон изменения температуры вдоль хорды профиля лопатки

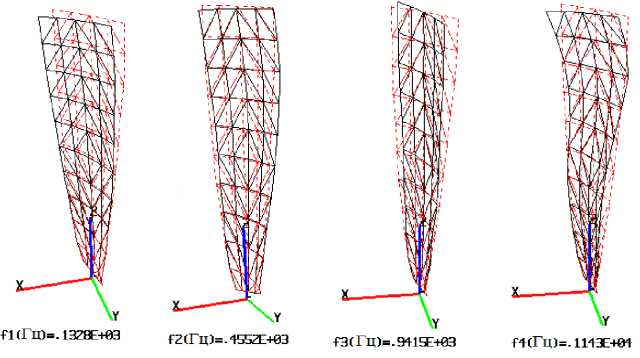
Рис. 4. Формы колебаний лопатки без влияния температуры

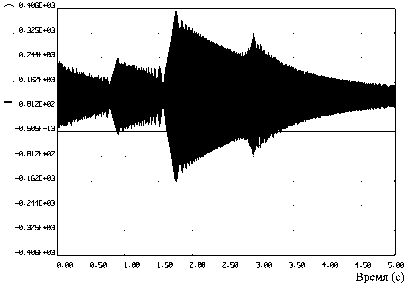
а

Рис. 5. Изменение напряжений по времени: а – при расчете; б – при эксперименте

Напряжение (МПа)

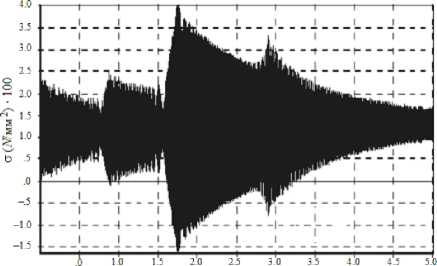
Time (s)

б

Таблица 3

Форма колебаний	Собственные частоты (Гц) в зависимости от температуры
	0 °C	100 °C	Δ f , %	200 °C	Δ f , %	300 °C	Δ f , %
f1 (1 И)	132,79	128,77	–3,03	120,47	–9,28	100,56	–24,27
f2 (2 И)	455,15	441,44	–3,01	433,94	–4,66	377,63	–17,03
f3 (1 К)	941,53	907,75	–3,59	890,96	–5,37	792,02	–15,88
f4 (3 И)	1142,6	1104,73	–3,31	1084,16	–5,11	1047,78	–8,30
Долговечность лопатки Демпфирование LOW	0,992 7 E + 08	0,102 58 E + 08		0,862 30 E + 07		0,904 7 E + 06
(число циклов)      Демпфирование HIGH	0,854 1 E + 09	0,141 0 E + 09		0,987 1 E + 08		0,861 3 E + 07

Таблица 4

Форма колебаний		Собственные частоты (Гц) в зависимости от температуры
		0 °C	100 °C	Δ f , %	200 °C	Δ f , %	300 °C	Δ f , %
f1 (1 И)		161,19	155,85	–3,31	150,11	–6,87	148,68	–7,76
f2 (2 И)		479,86	466,77	–2,73	459,58	–4,23	458,71	–4,41
f3 (1 К)		946,54	912,69	–3,58	895,92	–5,35	897,47	–5,18
f4 (3 И)		1164,56	1126,98	–3,23	1106,68	–4,97	1104,92	–5,12
Долговечность лопатки (число циклов)	Демпфирование LOW	0,692 7 E + 08	0,902 582 E + 07		0,162 30 E + 07		0,194 7 E + 06
	Демпфирование HIGH	0,354 1 E + 09	0,851 0 E + 08		0,127 1 E + 08		0,101 3 E + 07

Таблица 5

Форма колебаний		Собственные частоты (Гц) в зависимости от температуры
		0 °C	100 °C	Δ f , %	200 °C	Δ f , %	300 °C	Δ f , %
f1 (1 И)		224,39	211,9803	–5,53	210,787	–6,06	209,358	–6,70
f2 (2 И)		544,16	532,088	–2,22	525,593	–3,41	524,919	–3,54
f3 (1 К)		960,61	926,5323	–3,55	909,746	–5,30	911,528	–5,11
f4 (3 И)		1224,43	1187,194	–3,04	1167,31	–4,67	1166,21	–4,75
Долговечность лопатки (число циклов)	Демпфирование LOW	0,572 7 E + 08	0,802 58 E + 07		0,112 30 E + 07		0,174 7 E + 06
	Демпфирование HIGH	0,314 1 E + 09	0,755 0 E + 08		0,107 1 E + 08		0,991 3 E + 06

Собственные частоты колебаний и долговечность лопатки с различными величинами температуры при числе оборотов ротора Ω = 0 1/c

Собственные частоты колебаний и долговечность лопатки с различными величинами температуры при числе оборотов ротора Ω = 50 1/c

Собственные частоты колебаний и долговечность лопатки с различными величинами температуры при числе оборотов ротора Ω = 100 1/c

Данные таблиц показывают, что во всех случаях число циклов до разрушения лопатки уменьшается более чем в 6 раз при увеличении температуры на 100 °C (см. величины долговечности в табл. 3–5).

Следующим этапом расчета исследована замена стали 15X12BНМФ лопатки сплавами ЭИ-598 и ЭИ-437, которые имеют предел выносливости соответственно 250 и 305 МПа; число циклов до разрушения 108 [6]. Результаты расчета числа циклов до разрушения лопатки турбомашины для стали 15X12BНМФ и сплавов ЭИ-598 и ЭИ-437 без учета температуры представлены в табл. 6.

Видно, что чем выше предел выносливости материала, тем больше число циклов до разрушения лопатки.

Таким образом, установлено, что температура оказывает значительное влияние на динамические харак- теристики и число циклов до разрушения лопаток турбомашин. Собственные частоты колебаний уменьшаются от влияния температуры от 6 % – при максимальных оборотах вращения (100 1/c) до 24 % – при нулевом вращении. При увеличении температуры на 100 °C число циклов до разрушения лопатки уменьшается более чем в 6 раз для всех случаев.

Таблица 6

Результаты расчета долговечности лопатки турбомашины при использовании различных сплавов

Материал	Долговечность (число циклов)
15X12BНМФ	0,992 7 E + 08
ЭИ-598	0,450 41 E + 9
ЭИ-437	3,240 03 E + 9

Результаты расчета показывают, что изменение жесткости конструкции лопаток турбомашин, обусловленное температурой и центробежными силами, оказывает значительное влияние на их динамические характеристики и усталостную прочность лопаток. Поэтому при проектировании лопаток турбомашин для обеспечения их надежности необходимо учитывать изменение жесткости конструкции лопаток от температуры и центробежных сил.

Расчет на усталостную прочность лопатки с разными вариантами коэффициентов демпфирования показывает, что число циклов до разрушения лопаток может быть увеличено более чем в 9 раз путем увеличения демпфирования колебаний лопатки.

Результаты расчета на усталостную прочность лопаток турбомашин с учетом изменения жесткости конструкции лопаток от температуры и центробежных сил позволяют уточнить подходы к повышению их ресурса. Для повышения ресурса лопаток турбомашин необходимо применять демпфирование колебаний лопатки, снижать тепловой поток в материале лопатки, охлаждать лопатки.

К методам демпфирования колебаний лопаток относятся такие методы, как использование материалов, которые имеют свойства высокого демпфирования, например, стеклопластиков; методы механического демпфирования в замке и стыке лопатки (демпфирование трения); методы аэродинамического демпфирования.

К методам снижения теплового потока в материале лопаток относятся такие методы, как использование теплозащитных покрытий из керамических материалов с низкой теплопроводностью; использование покрытий для повышения жаростойкости материала (например, из окиси алюминия); использование металлических многокомпонентных покрытий для повышения жаростойкости материала (например, покрытия из четырех компонентов: никель–хром– алюминий–итрий).

К методам охлаждения лопатки относятся такие методы, как конвективный (путем съема тепла потоком воздуха с внутренних поверхностей охлаждающих каналов в лопатках и других деталях с последующим выпуском воздуха в проточную часть), пленочный (завесный, заградительный) и проникающий.