Разработка математических моделей для оценки амплитуды кромковой волнистости гнутолистовых тонких профилей при их серийном производстве

Для оценки влияния величин остаточных продольных деформаций растяжения в тонких краевых элементах профиля на значения амплитуды волнистости кромок, зададим функцию прогиба кромки полки от недеформированного состояния в синусоидальном виде (рис. 1):

to (x ) = ю _м sin(2 л x / T ), (1) где to M — амплитуда краевой волнистости (по кромке); x – продольная координата;

T – период волнистости.

Длину растянутой кромки l на длине периода Т определим по известному выражению дифференциальной геометрии:

+ 0,5 Т ,------------------------ l = | д/1 + [го^x )]2 dx

- 0,5 Т

Решим приближенно данный интеграл, разложив выражение под корнем в степенной ряд с точностью до четвертого порядка (сокращенный ряд Тейлора). Введя ряд упрощений и выполнив математические преобразования, получим: l = T [ 1 + 0,25 to M п ² Т ^-т + 4,68 - 10 ^{- 2} го М п ⁴ Т ^{- 4} ] .(3)

Тогда величина относительной деформации растяжения полки (по кромке) относительно недеформированной в продольном направлении зоны сгиба и неподгибаемых элементов равна:

si =[0,25гоМп2Т-2 + 4,68-10-2гоМп4Т-4 ]. (4)

Ввиду малости последнего члена выражения (4) получим равенство, связывающее значения относительных остаточных деформаций растяжения в кромке отформованной полки с амплитудой волнистости этой кромки равной to M при условии прямолинейности готового профиля [1]: s ,=^ m» M /2 T )².             (5)

Приравнивая выражение, полученное на основе геометрических параметров зоны плавного перехода и заготовки, угла подгибки за проход и механических свойств деформируемого материала, к равенству (5) имеем следующую зависимость амплитуды волнистости кромки ( с = b ) от режимов профилирования:

toM = (T/л)) - [0,5b 2(Д d(arcsin[sin(a) -

• •[(/ + C1)-cht +(C41-1)-sht]])/5t)2 -aSIE]0,5. (6)

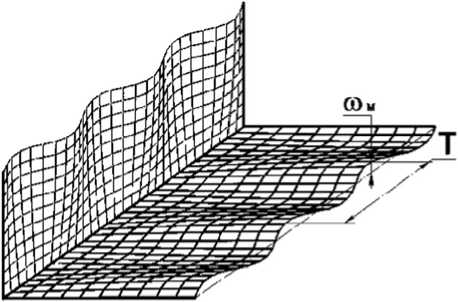
Рис. 1. Параметры синусоидальной кромковой волнистости

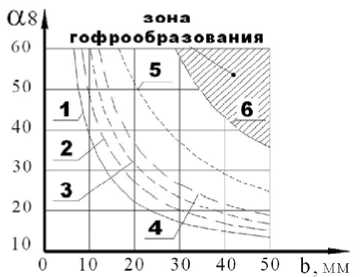
Рис. 2. Предельные углы подгибки при s, мм:

1- 0,4; 2 - 0,5; 3 - 0,6; 4 - 0,7; 5 - 1,0; 6 - 1,5

Графическая зависимость предельных углов подгибки за проход плоских элементов в роликовых парах представлена на рис. 2 (материал заготовки – В95АМ, А = 400 мм.).

Зависимость (6) позволяет оценить значения амплитуды синусоидальной краевой волнистости по кромкам отформованных полок в случае превышения критических углов, и показана графически на рис. 30а, в зависимости от ширины полок для углов подгибки равных 20°, 30°, 40° (соответственно прямые 1, 2, 3) и на рис. 3,б, в зависимости от углов подгибки за проход для ширины элементов 30, 40, 60 мм (соответственно кривые 1, 2, 3). Для обоих случаев материал заготовки – В95АМ, А = 400 мм. Длина периода волнистости Т = 2b .

Углы подгибки по временным параметрам можно выразить через гиперфункции в виде:

• b – ширина подгибаемого элемента;

• s₀ – толщина исходной листовой заготовки;

• A – межклетьевого расстояния;

С ₅ и Е - механических свойств профилируемой заготовки.

Для определения амплитуды кромковой волнистости (6) еще необходима длина периода волнистости Т , которая не всегда равна 2b .

Средняя равномерно распределенная по длине дуги кругового элемента остаточная деформация растяжения £_t :

b

St = b-1 ’J ^ ост (A b) dAb,     (8)

где A b - текущее положение точки на дуге кругового сектора криволинейной полки.

Для оценки значений относительных остаточных деформаций при допущении о полной разгрузке напряжений сжатия в кромках криволинейных полок рассмотрим участки изломов как волны с амплитудой по кромке to м длиной l и периодом Т (рис. 4):

to = toMexp (-а2 x2),        (9)

где а = 2 l ^-1 – коэффициент затухания функции прогиба при удалении от х = 0 .

Удлинение кромки на участке волны длиной l определим и используем интегральную зависимость длины кривой известную из дифференциальной геометрии:

ch (t) = (e + e-t)/2;

sh (t) = (et - e-t);

th (t) = sh (t)/ ch (t)   и т.д. (7)

Получим значения предельно допустимых углов подгибки плоских тонкостенных полок на данном технологическом переходе валковой пары в зависимости от основных параметров профилирования:

A l =

+ 1 /2

J

_ - 1 /2

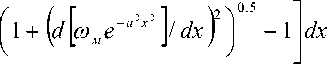
Длина кромки волны:

1 к =

'+ 1 /2

J[1 + (d[toM exp(-а2x2)]/

.- 1 /2

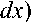
. (10)

На единице длины профиля общая длина кромки волн с количеством n = Т^-1 равна:

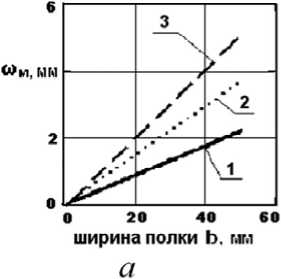
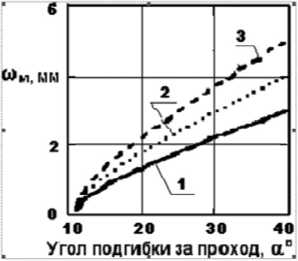
Рис. 3. Амплитуда кромковой волнистости:

а – в зависимости от ширины подгибаемой плоской полки; б – в зависимости от угла подгибки за проход

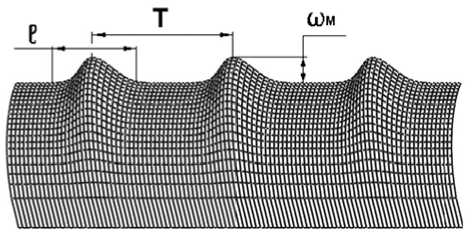
Рис. 4. Геометрия изломов на криволинейных отформованных полках

² l н = l • = l kT ^- .       (11)

Общая длина на единице длины невозмущенных частей кромки равна:

2 l -1- l -T¹ .               (12)

В итоге относительная остаточная деформа-

ция по кромке определится выражением

£ ост = [ 2 l н + 2 l k -1] =

= l _k•Т^-1 + (1 - l •Т^-1) –1 = Т^-1• ( l _k - l ) .

^£ ОСТ

= Т ^{- 1}

■+ 1 /2

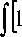
.- 1 /2

+ ( d to^ exp( - а ² x ² ) ] / dx ) ² p dx - 1

. (13)

На рис. 5а и рис. 5б показаны уровни средней продольной остаточной деформации в отформованных элементах в зависимости, соответственно, от амплитуды излома w_M и длины излома l .

Рис. 5а: Т = 50 мм; to М = 0_4,0 мм; кривые 1; 2; 3; 4 соответственно при l = 20 мм; 15 мм; 10 мм; 5 мм. Рис. 5б: Т = 50 мм; l = 5…20 мм; кривые 1; 2; 3; 4 соответственно при to М = 1,0 мм; 2,0 мм; 3,0 мм; 4,0 мм.

Для определения амплитуды to М изломов повторяющихся с периодом Т приравняем функциональную зависимость средних остаточных продольных деформаций (8) с выражением (7), и, решая полученное уравнение в системе UNIGRAPhics относительно амплитуды изломов to М , получим решение, показанное графически на рис. 6. Углы подгибки (по кромкам) криволинейных полок шириной b = 25 мм равны – 30°, 60°, 90° (соответственно кривые 1, 2, 3) при этом углы центральных секторов отформованной полки равны – 60°,120°,180°; материал заготовки В95АМ; А = 400 мм.

Амплитуда периодических изломов для углов подгибки 30° и 60° изменяется почти в 2 раза,

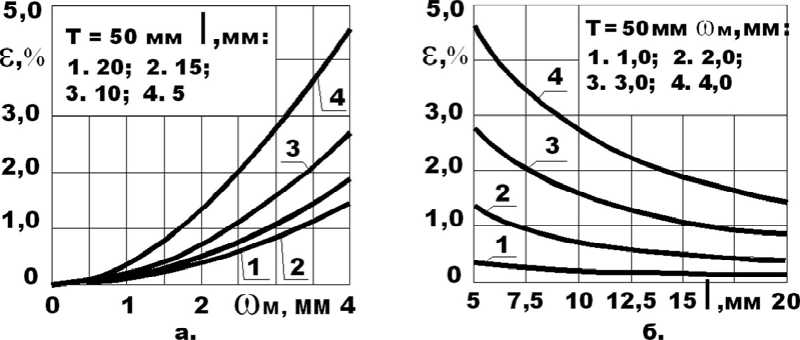
Рис. 5. Остаточная продольная деформация: а – в зависимости от амплитуды изломов; б – в зависимости от длины излома

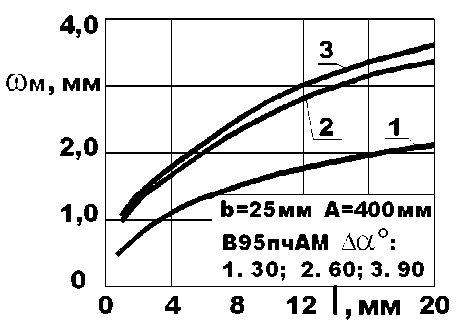
Рис. 6. Амплитуда периодических изломов

а для углов 60° и 90° - не более 10 %. Такое объясняется изменением средних продольных остаточных деформаций с 0,26% до 0,73 % - для первого случая, и с 0,73 % до 0,84 % - для второго случая. Далее оценим значения прогибов симметричных профилей , когда отмечается крутка асимметричных профилей от накопленных в процессе формообразования продольных остаточных деформаций.

Здесь криволинейные подгибаемые участки устойчивость не теряют и изломы не возникают.

Для симметричных профилей поводка (прогиб) величиной to у на одном погоном метре длины определит продольный радиус изгиба R_y и

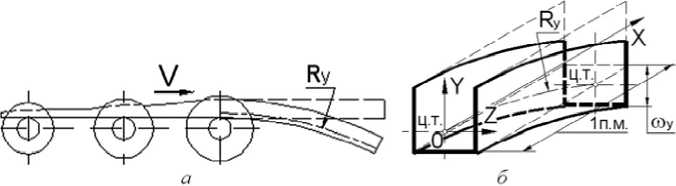
Рис. 7. Прогиб профиля от продольных остаточных деформаций: а – направление прогиба профиля после формообразования; б – расчетная схема для определения прогиба

центральный угол сектора ϕ с длиной дуги равной L = 1 метр из системы уравнений (рис. 7):

! ω _у = R_y (1-cos ϕ /2 );

IL= R y · ϕ .

Или, если приравнять длину дуги длине хорды: ! ω _у= R_y(1-cos ϕ /2);

L L = ^у 2R_y· ^y sin ϕ /2 .             (14)

Решая систему уравнений (14) относительно R_y и ϕ получим:

R_y = (0,25L² + ω ²_у) · (2 ω _у)^-1 _.   (15)

Изгиб профиля (прогиб) в вертикальной плоскости происходит относительно центра жесткости сечения профиля – для швеллера у_с=b² . (В +2b)^-1 [2] (рис. 8а), где В - ширина стенки швеллера. Деформация растяжения кромки т. А равна:

ε _А = (b - у_с)·R_y^-1 ,            (16)

где (b – у_с) – расстояние в вертикальной плоскости от центра тяжести готового профиля до кромок полок.

Принимая, что при прогибе профиля от неравномерного распределения остаточных продольных деформаций растяжения по ширине отформованных элементов (рис. 8б), происходит полная разгрузка продольных напряжений в сечении профиля, приравняем среднее значение остаточных деформаций к деформациям растяжения на кромке профиля при его изгибе в вертикальной плоскости (16). И определим прогиб профиля w при подстановке значения R из (15) в (16). ^{y y}

Решение задачи определения поводок графически представлено на рис. 9, где показаны значения прогиба на погонном метре длины профиля (рис. 9а) и радиуса продольной кривизны профиля (рис. 9б) в зависимости от отношения ширины стенки к ширине полки ( b = 50 мм) В/b

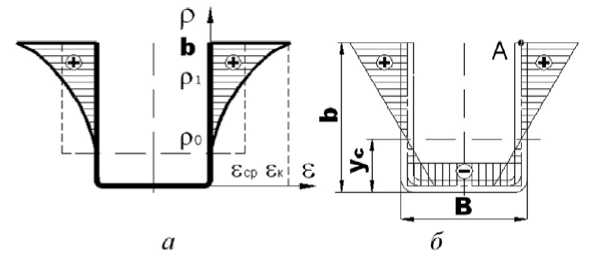
Рис. 8. Распределение продольных деформаций по ширине элементов швеллера: а - при прогибе вниз; б – остаточных после формовки профилированием

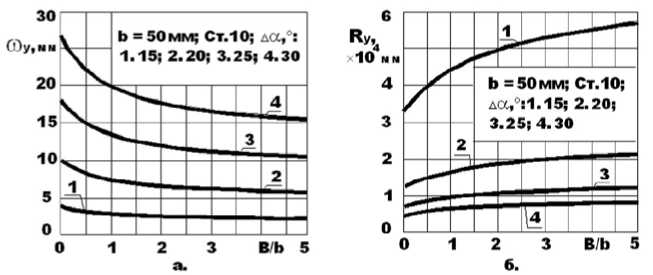
Рис. 9. Поводки равнополочных швеллеров после профилирования а – прогиб профиля на одном погонном метре; б – продольная кривизна профиля

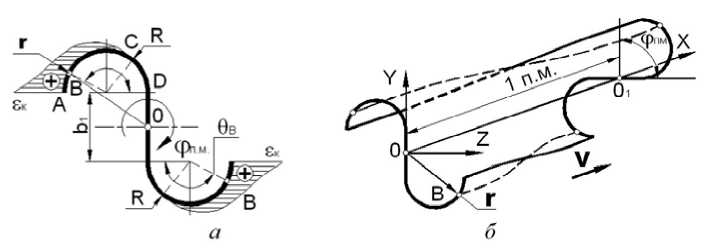
Рис. 10. Крутка асимметричного профиля от остаточных деформаций: а – поперечное сечение отформованного профиля;

б – крутка на одном погонном метре длины профиля

и угла подгибки за проход (15°, 20°, 25°, 30° – соответственно кривые 1, 2, 3, 4). Материал заготовки – Ст.10.

Крутка асимметричных профилей возникает при профилировании несимметричных и особо асимметричных профилей, на которых кроме прогиба возникают поводки типа саблевиднос- ти и крутки.

Распределение остаточной деформации по длине дуги кругового сектора имеет вид функциональной зависимости (рис. 10):

б ост = б ост (Ab). (17)

Расстояние от материальной точки угловых деформаций до точки, являющейся центром тяжести эпюры распределения продольных деформаций растяжения по ширине криволинейной полки Db_B вычислим из равенства:

A b B                    b

J 6(Ab)dAb = J 6(Ab)dAb

A b о                    ^A b B

где величина Db_B – расстояние от сопряжения уголковой зоны с плоским подгибаемым элементом до центра тяжести эпюры распределения остаточных деформаций – для плоских подгибаемых элементов или длина дуги от сопряжения криволинейного подгибаемого элемента с прямолинейным (не подгибаемым) элементом заготовки – для криволинейных подгибаемых полок.

Геометрическое расположение точки раздела зоны с остаточными продольными деформациями в отформованной полке и зоны без остаточных деформаций определено из равенства б ( А b о ) = 0 . Винтовая линия движения точки В лежит на цилиндрической поверхности радиуса r . Радиус r определим из геометрических параметров поперечного сечения (рис. 10а): r = [ ( 0,5 b + R sin ^ ) 2 + ( R ² cos²< 9 _S ^Р , (19)

,1             B                     B где 0B = AbBR-1 - угол местоположения точки В на круговом секторе; b1 – ширина плоского (не подгибаемого) участка.

В цилиндрической системе координат винтовую линию движения точки В представим в параметрическом виде уравнениями вида:

X = A • ф ; Y = r • sin ф ; Z = r • cos ф , где А = 1/ ф пм [M /°] - обратная величина углу крутки на погонный метр профиля.

Длину винтовой линии определим из дифференциальной геометрии как:

^ФПМ\,        х₂               42     оЮ’5                ч\05

L = J [ ( r cos ф )² + ( - r cos ф )² + A ² ] d ф = ( r ² + A ² ) • ф _ПМ .

Относительная продольная деформация растяжения материальных точек закрученных по винтовой линии с радиусом r будет равна: ^б ост =^{( L} - ! ) • 1 1 = ( [ ^ ПМ • r ^{) 2 +} 1 ]⁰ - ^{1 ) .}

Откуда имеем выражение для определения угла крутки профиля на единице длины в зависимости от средней остаточной деформации:

фПМ = r4 •[(бост + 1)2 - 1]0,5. (20)

Графическое отображение углов крутки одного погонного метра асимметричного профиля ( Z -образного сечения) от отношения ширины плоского недеформируемого участка стенки b₁ к длине дуги подгибаемой полки b = 25 мм (рис. 11). Материал заготовки Д16АМ, А = 400 мм. Кривые 1, 2, 3 соответствуют углам подгибки кромки криволинейной подгибаемой полки (в

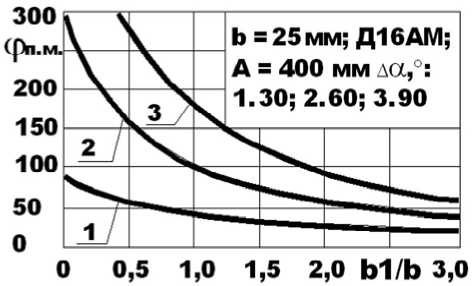
Рис. 11. Угол крутки Z-образного профиля после отформовки на предварительных переходах плане круговой сектор) на углы 30, 60, 90°.

На основании вышеизложенного вытекает необходимость проверки математических моделей для оценки амплитуды кромковой волнистости методом графоаналитического моделирования параметров технологического процесса изготовления тонкостенных гнутолистовых профилей.