Разработка математических моделей для прогнозирования падения усилий по основе и утку полушерстяных камвольных тканей в процессе термофиксации

Автор: Гапонова Т.А., Садовский В.В., Братченя Л.О.

Журнал: Вестник Витебского государственного технологического университета @vestnik-vstu

Рубрика: Технология и оборудование легкой промышленности и машиностроения

Статья в выпуске: 2 (39), 2020 года.

Бесплатный доступ

Статья посвящена исследованию изменения усилий (напряжений) по основе и утку полушерстяных камвольных тканей различного волокнистого состава, возникших при их двухосной деформации, после воздействия сухого горячего воздуха в течение определенного времени. Для проведения данного исследования был применен центральный композиционный ортогональный план, позволяющий построить уравнение регрессии второго порядка для трех факторов. По результатам исследования были получены математические модели, позволяющие прогнозировать падение усилия по основе и утку тканей при их деформации по основе и утку и времени воздействия горячего воздуха, построены графики зависимости падения усилий по основе и утку от времени воздействия горячего воздуха при постоянных величинах деформаций по основе и утку, а также двумерные сечения падения усилия по основе и утку от величин деформации в обоих направлениях при постоянном времени воздействия температуры. Было выявлено, что на величину падения усилия по основе и по утку будут оказывать влияние состав, поверхностная плотность, плотность ткани по основе и утку, линейная плотность нитей основы и утка, а также величины деформации ткани по основе и утку и время воздействия горячего воздуха. Результаты исследования позволяют определить оптимальные условия проведения процесса термофиксации.

Еще

Камвольная ткань, термофиксация, двухосное растяжение, релаксация усилий

Короткий адрес: https://sciup.org/142224656

IDR: 142224656 | DOI: 10.24411/2079-7958-2020-13903

Текст научной статьи Разработка математических моделей для прогнозирования падения усилий по основе и утку полушерстяных камвольных тканей в процессе термофиксации

WORSTED FABRIC, THERMAL FIXATION, BIAXIAL TENSION, TENSION RECOVERY

The article discusses the research of the stress decrease along the warp and weft of half-woolen worsted fabrics by biaxial tension and exposure to hot air for a certain time. Based on the results of the research, mathematical models were constructed that enabled to predict a change in the stress during its relaxation after biaxial deformation during thermal fixation. It was revealed that the structural characteristics of the fabric, its composition, the amount of deformation and the duration of exposure to hot air influence the magnitude of the stress decrease. It was established that the maximum value of the stress arising in the process of stretching is observed at the greatest deformation, and the maximum stress decrease occurs when exposed to temperature for 220-300 seconds, depending on the amount of deformation and the type of fabric.

утку и время воздействия горячего воздуха. Результаты исследования позволяют определить оптимальные условия проведения процесса термофиксации.

Важной частью отделки камвольных тканей является процесс термофиксации, целью которого является придание ткани фиксированных размеров по ширине, а также снятие внутренних напряжений в ее структуре. Для достижения этого ткань подвергается одновременной деформации на заданные величины по основе и утку и воздействию горячего воздуха в течение определенного времени. Указанные параметры можно регулировать, добиваясь максимального падения усилия (напряжения), возникающего в ткани при ее деформировании и тем самым находить оптимальные условия проведения процесса термофиксации.

Существует ряд работ, касающихся исследования деформационных свойств текстильных материалов, в том числе и камвольных тканей, различных по составу [1–3]. Однако исследований деформационных процессов камвольных тканей, содержащих в своем составе шерстяные волокна и полиэстер в различных сочетаниях, а также лайкру, при различных вариантах двуосного растяжения и воздействия температуры, не проводились. В связи с этим целью данной ра- боты была оценка и прогнозирование влияния деформационных и температурных воздействий на падение усилий по основе и утку указанных камвольных тканей. Для достижения данной цели была поставлена задача разработать математические модели, позволяющие оценить и спрогнозировать падение усилий по основе и утку камвольных тканей, состоящих из шерстяных волокон, полиэстера и лайкры в различном сочетании при их двухосной деформации и воздействии горячего воздуха.

Для изучения влияния величины деформации по основе и по утку, и времени воздействия горячего воздуха на падение усилий по основе и по утку было проведено исследование, которому подвергались камвольные ткани, характеристики которых представлены в таблице 1.

Перед экспериментом образцы тканей заваривались по методике, соответствующей производственной, высушивались и выдерживались в эксикаторе в течение 24 часов. Затем смачивались умягчающей и антистатической пропиткой, приготовленной по рецептуре, используемой на производстве: Гидроперм RSHA 30 грамм на 1

Таблица 1 – Характеристики исследуемых тканей
s z H ra м ra Q. VO О 01 z	о z о H о c о Q. c	Состав ткани	S 1 о л* я	Количество нитей на 10 см ткани		Состав нитей		Линейная плотность нитей, текс		Крутка, кр/м
s z H ra м ra Q. VO О 01 z	о z о H о c о Q. c	Состав ткани	S 1 о л* я	га СП о и о	о н >4	основа	уток	га СП о и о	о н >4	га СП о и о	о н >4
1	Саржа 2/1	Ш – 66 %, ПЭ – 34 %	280	310	238	Ш – 70 %, ПЭ – 30 %	Ш – 70 %, ПЭ – 30 %	50	50	550	550
2	Саржа 2/2	Ш – 27 %, ПЭ – 73 %	211	280	226	Ш – 30 %, ПЭ – 70 %	Ш – 30 %, ПЭ – 70 %	42	42	672	672
3	Саржа 2/1	Ш – 43 %, ПЭ – 55%, Л – 2 %	210	313	194	Ш – 50 %, ПЭ – 50 %	Ш – 48,1 %, ПЭ – 48,1 %, Л – 3,8 %	38	42,4	650	646

Примечание: Ш – шерсть, ПЭ – полиэстер, Л – лайкра.

литр воды смешанный с 30 % раствором уксусной кислоты в количестве 2 грамма на 1 литр воды. Эксперимент проводился на установке, позволяющей создавать различные варианты двухосной плоскостной деформации ткани, в том числе при воздействии температуры [4].

В качестве факторов воздействия были взяты: величина деформации по основе ( x₁ ), величина деформации по утку ( x₂ ) и время воздействия сухого воздуха при температуре 180 °C ( х₃ ).

Исследование проводилось на разработанной авторами установке, позволяющей создавать различные варианты двухосной плоскостной деформации ткани, в том числе при воздействии температуры, и при этом измерять усилия при деформировании, падение усилия после деформирования, воздухопроницаемость и пористость ткани при различных вариантах деформирования. Испытанию подвергались образцы тканей размером 100 х 100 ìì .

Параметрами выхода были: Y₁ – падение усилия по основе (%), Y₂ – падение усилия по утку (%), которые определялись следующим образом:

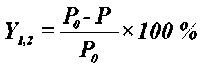
где P₀ – усилие, необходимое для растяжения ткани по основе (утку) на определенную величину деформации, Í ; P – усилие по основе (утку), зарегистрированное после воздействия сухого горячего воздуха в течение заданного времени, Í .

Параметры выхода Y1 и Y2 помогают установить, при какой длительности воздействия высокой температуры возникшее при деформировании ткани усилие максимально падает после прекращения деформирования.

Для проведения эксперимента использовался центральный композиционный ортогональный план (ЦКОП), позволяющий построить уравнение регрессии второго порядка для трех факторов.

Уровни варьирования факторов представлены в таблице 2, план эксперимента – в таблице 3.

Для того чтобы матрица планирования обладала свойством ортогональности, были введены столбцы с корректированными значениями уровня x', которые вычислялись по формуле:

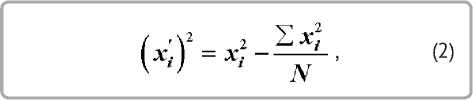
где N – количество опытов, равное 1.

Матрица для расчета коэффициентов уравнения представлена в таблице 4, в которой столбцы 2–11 представляют собой ортогональную матрицу планирования, столбцы 6–8 рассчитываются по формуле (2). Столбец 2 вводится для придания матрице ортогональности.

Величины падения усилия по основе Y₁ и падения усилия по утку Y₂ в процессе релаксации тканей, полученные после проведения соответствующего номера опыта в плане эксперимента (таблица 3) представлены в таблице 5. Опыт № 15 (центральная точка плана эксперимента) для определения ошибки воспроизводимости эксперимента повторялся трижды.

Коэффициенты уравнений регрессии рассчитывались в соответствии с данными таблиц 4 и 5 по известным формулам [5]. После проверки их значимости были получены и проверены на адекватность математические модели падения усилия по основе ( Y₁ ) и падения усилия по утку

Таблица 2 – Уровни варьирования факторов

Факторы	Код x_i	Уровни факторов					Интервал варьирования факторов
Факторы	Код x_i	-1,215	-1	0	+1	+1,215	Интервал варьирования факторов
Деформация ткани по основе, %	x₁	1,4	1,9	4,4	6,9	7,3	2,5
Деформация ткани по утку, %	x₂	1,4	1,9	4,4	6,9	7,3	2,5
Время воздействия воздуха при температуре 180 °C , с	x₃	59	80	180	280	302	100

Таблица 3 – План трехфакторного эксперимента

№ опыта	Натуральные значения факторов			Кодированные значения факторов
№ опыта	x₁	x₂	x₃	x₁	x₂	x₃
1	1,9	1,9	80	-1	-1	-1
2	6,9	1,9	80	+1	-1	-1
3	1,9	6,9	80	-1	+1	-1
4	6,9	6,9	80	+1	+1	-1
5	1,9	1,9	280	-1	-1	+1
6	6,9	1,9	280	+1	-1	+1
7	1,9	6,9	280	-1	+1	+1
8	6,9	6,9	280	+1	+1	+1
9	1,4	4,4	180	-1,215	0	0
10	7,3	4,4	180	+1,215	0	0
11	4,4	1,4	180	0	-1,215	0
12	4,4	7,3	180	0	+1,215	0
13	4,4	4,4	59	0	0	-1,215
14	4,4	4,4	302	0	0	+1,215
I 15	4,4	4,4	180	0	0	⁰ ____)

Таблица 4 – Матрица для расчетов коэффициентов уравнения регрессии для трехфакторного эксперимента
№ опыта	Матрица эксперимента
№ опыта	x₀	x₁	x₂	x₃	(x 1 ')²	(x 2 ')²	(x 3 ')²	x₁•x₂	x₁•x₃	x₂•x₃
1	2	3	4	5	6	7	8	9	10	11
1	+1	-1	-1	-1	+0,27	+0,27	+0,27	+1	+1	+1
2	+1	+1	-1	-1	+0,27	+0,27	+0,27	-1	-1	+1
3	+1	-1	+1	-1	+0,27	+0,27	+0,27	-1	+1	-1
4	+1	+1	+1	-1	+0,27	+0,27	+0,27	+1	-1	-1
5	+1	-1	-1	+1	+0,27	+0,27	+0,27	+1	-1	-1
6	+1	+1	-1	+1	+0,27	+0,27	+0,27	-1	+1	-1
7	+1	-1	+1	+1	+0,27	+0,27	+0,27	-1	-1	+1
8	+1	+1	+1	+1	+0,27	+0,27	+0,27	+1	+1	+1
9	+1	-1,215	0	0	+0,74	-0,73	-0,73	0	0	0
10	+1	+1,215	0	0	+0,74	-0,73	-0,73	0	0	0
11	+1	0	-1,215	0	-0,73	+0,74	-0,73	0	0	0
12	+1	0	+1,215	0	-0,73	+0,74	-0,73	0	0	0
13	+1	0	0	-1,215	-0,73	-0,73	+0,74	0	0	0
14	+1	0	0	+1,215	-0,73	-0,73	+0,74	0	0	0
15	+1	0	0	0	-0,73	-0,73	-0,73	0	0	⁰

Таблица 5 - Результаты измерения падения усилия по основе ( Y 1 ) и усилия по утку ( Y 2 ) тканей в процессе каждого опыта плана эксперимента

№ опыта	Номера образцов тканей
	1		2		3
	Y, %	Y, %	Y, %	Y, %	Y, %	Y, %
1	34,6	45,6	31,0	43,5	11,0	8,7
2	49,1	50,7	38,9	48,3	30,0	14,0
3	54,4	63,2	45,6	52,9	31,6	18,0
4	84,0	85,8	74,5	80,8	71,0	40,6
5	69,0	77,4	60,0	77,0	49,7	37,0
6	72,8	77,5	62,5	75,1	55,5	43,0
7	83,0	84,7	71,7	80,0	71,0	44,7
8	94,0	94,4	87,0	85,3	88,0	63,0
9	62,1	71,8	52,3	71,3	38,4	30,0
10	79,3	83,2	70,1	79,8	65,6	45,7
11	59,9	68,5	48,4	67,0	32,4	25,5
12	88,5	90,0	79,0	83,6	73,0	49,0
13	39,1	47,4	32,5	45,4	23,0	12,2
14	74,5	79,8	65,7	74,9	62,0	45,1
15	64,0	75,3	57,4	73,0	45,5	37,4

Таблица 6 – Математические модели падения усилия по основе ( Y₁ ) в процессе релаксации ткани
№ образца ткани	Уравнение регрессии
1	Y = 66,0 + 7,3 x₁ + 11,4 x ₂ + 12,8 x ₃ + 2,9 x ² + 5,3 x 2 - 6,5 x ₃ ² + 2,8 x₁ x ₂ - 3,7 x₁ x ₃ - 2,4 x ₂ x₃
2	1 1 = 57,5 + 7,0 x ₁ + 11,3 x ₂ + 12,0 x 3 + 2, 6 x ² + 4,3 x ₂ ² - 5,6 x ₃ ² + 4,2 x ₁ x ₂ - 2, 4 x ₁ x 3 - 1,8 x ₂ x 3
3	Y = 46,7 + 10,4 x ₁ + 15,1 x ₂ + 15,4 x ₃ + 3,4 x ² + 3,9 x ₂ ² - 3,0 x ₃ ² + 4,0 x ₁ x ₂ - 4,5 x ₁ x ₃ - 1,0 x ₂ x ₃

Таблица 7 – Математические модели падения усилия по утку ( Y₂ ) в процессе релаксации ткани
№ образца ткани	Уравнение регрессии
1	Y₂ = 75,2 + 4,7 x ₁ + 9,4 x ₂ + 11,7 x ₃ + 1,7 x 2 + 2,9 x 2 - 7,7 x ₃ ² + 3,4 x ₁ x ₂ - 2,2 x ₁ x ₃ - 3,6 x ₂ x ₃
2	Y ₂ = 73,2 + 4,2 x ₁ + 6,9 x ₂ + 11,7 x ₃ + 1,7 x ² + 1,5 x ₂ ² - 8,7 x ₃ ² + 3,8 x ₁ x₂ - 3,7 x ₁ x ₃ - 3,6 x₂x ₃
3	Y₂ = 36,5 + 6,5 x ₁ + 8,4 x ₂ + 13,4 x ₃ + 1,2 x ^ + 0,8 x 2 - 5,0 x ₃ ² + 3,7 x ₁ x ₂ - 1,0 x ₂ x ₃
к_________

( Y 2 ) исследуемых тканей, которые представлены, соответственно, в таблицах 6 и 7.

Анализируя полученные модели, можно отметить, что модель для ткани 3 отличается от моделей для тканей 1 и 2 отсутствием парного воздействия x 1 x₃ , в связи с его низкой значимостью. Вероятней всего, это связано с присутствием в утке ткани 3 лайкры, что повлияло на усилие, вызванное деформированием ткани, и в связи с этим на характер его падения в процессе релаксации.

Использовав полученные модели, были построены графики зависимости падения усилий по основе и утку от времени воздействия горячего воздуха ( х₃ ) при постоянных величинах деформаций по основе ( х 1 ) и утку ( х₂ ), которые представлены на рисунках 1 и 2.

Из графиков на рисунках 1 и 2 видно, что величины падения усилий по основе и утку в процессе релаксации после всех вариантов деформирования увеличиваются с увеличением времени воздействия горячего воздуха. При этом у тканей, не содержащих лайкру (1 и 2), они достигают максимальных значений по осно-

ве и утку при воздействии горячего воздуха в течение 220 секунд (при деформировании на 6,9 %) и 260 секунд (при деформировании на 1,9 и 4,4 %). При более длительном воздействии горячего воздуха падение усилий начинает заметно снижаться. Возможно это связано с сжатием (усадкой) тканей из-за длительного воздействия горячего воздуха. У ткани, содержащей лайкру (3), при деформировании на 6,9 % максимум падения усилий по основе и утку достигается за 300 с воздействия горячего воздуха.

Для прогнозирования падения усилий по основе и утку в процессе релаксации тканей при одновременном изменении двух факторов воздействия по полученным моделям построены двумерные сечения. В качестве переменных были взяты величины деформирования по основе ( х 1 ) и по утку ( х₂ ), а время воздействия температуры ( х₃ ) было постоянным, равным 220 с .

С учетом этого, математические модели, представленные в таблицах 6 и 7, были пересчитаны и в программе Wolfram Alpha Mathematica 11.3 построены двумерные сечения поверхностей отклика для всех исследуемых тканей

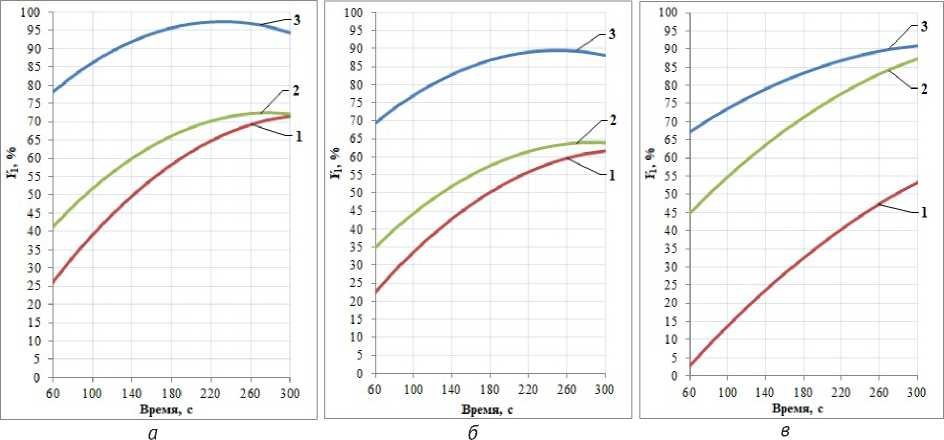
Рисунок 1 – Графики зависимости падения усилия по основе ( Y₁ ) тканей 1 (а), 2 (б), 3 (в) в процессе релаксации от времени воздействия горячего воздуха при различных величинах деформирования:

1 – x₁ = x₂ = 1,9 % ; 2 – x₁ = x₂ = 4,4 % ; 3 – x₁ = x₂ = 6,9 %

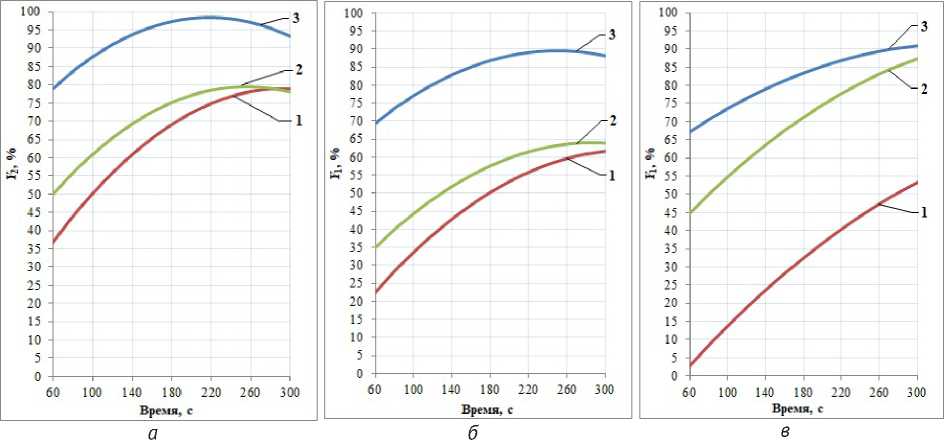
Рисунок 2 - Графики зависимости падения усилия по утку ( Y 2 ) тканей 1 (а), 2 (б), 3 (в) в процессе релаксации от времени воздействия горячего воздуха при различных величинах деформирования:

1 - х 1 = х₂ = 1,9 % ; 2 - х 1 = х₂ = 4,4 % ; 3 - х 1 = х₂ = 6,9 %

(рисунки 3 – 5).

Из сравнения двумерных сечений для разных тканей видно, что величины падения усилий по основе и утку в процессе релаксации тканей зависят не только от величин деформирования в данных направлениях, но также от линейной плотности нитей основы и утка и толщины (линейной плотности) этих нитей, которые в совокупности определяют величину усилия, необходимого для деформирования тканей на заданную величину. Естественно, что чем больше величина усилия деформирования, тем больше и величина его падения при релаксации.

Ткань 1 получена из нитей самой высокой линейной плотности в основе и утке (50 текс ) и имеет самые высокие плотности по основе и утку (соответственно 310 и 238 нитей/10 см ). Поэтому величина падения усилий по основе и утку у нее максимальная (до 95 – 97,5 %) среди исследуемых тканей (рисунок 3 а , б ).

У ткани 2 линейная плотность нитей в основе и утке ниже, чем у ткани 1 (42 текс ), также ниже и плотности по основе и утку (280 и 226 нитей/10 см ), вследствие этого величина падения усилий по основе и утку у нее меньше, соответственно, 85 и 90 % (рисунок 4 а , б ).

Ткань 3 в основе имеет нить с самой низкой линейной плотностью (38 текс ), а в утке нить с лайкрой (42,4 текс ). Наличие лайкры в утке при двухосном деформировании требует меньшего усилия не только по утку, но и по основе, а, следовательно, величина падения усилия при релаксации ткани также будет меньше. Поэтому при практически равных плотностях нитей по основе у тканей 1 и 3 (соответственно 310 и 313 нитей/10 см ), величины падения усилия при релаксации у них разные, соответственно, 95 и 85 % (рисунок 5 а ). Плотность по утку ткани 3 самая низкая (194 нити/10 см ), а также наличие лайкры являются причинами самого низкого падения усилия (до 60 %) при релаксации ткани (рисунок 5 б ).

Проведенное исследование показало, что максимальные величины падения усилия в процессе релаксации тканей достигаются при воздействии высокой температуры в течение 220 секунд и при деформировании их на максимальные величины. При этом величины падения усилий по основе и утку у тканей, не содержащих лайкру (1 и 2), близкие, а у ткани с лайкрой (3) они разные: по утку значительно меньше, чем по основе.

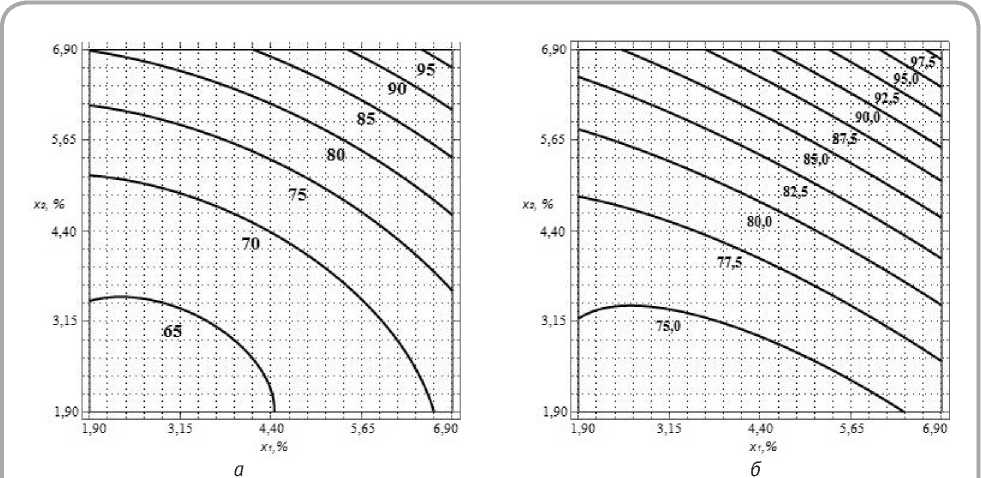
Рисунок 3 – Двумерные сечения поверхности отклика модели падения усилия по основе (а) и утку (б) в процессе релаксации ткани 1

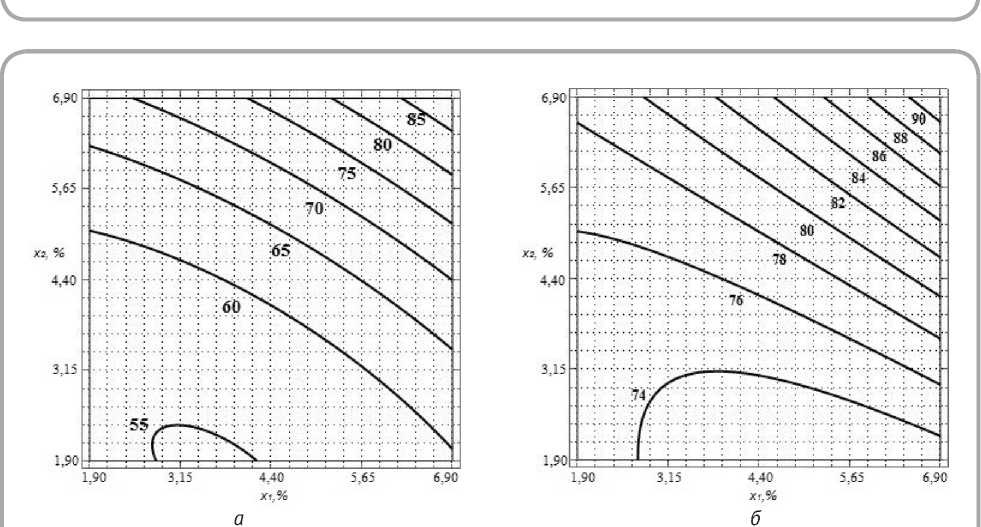
Рисунок 4 – Двумерные сечения поверхности отклика модели падения усилия по основе (а) и утку (б) в процессе релаксации ткани 2

ВЫВОДЫ

1. Разработаны математические модели и построены двумерные сечения поверхности отклика для оценки и прогнозирования падения усилий по основе и утку полушерстяных кам-
вольных тканей с различным содержанием шерсти и полиэстера, а также лайкры, после двухосного деформирования на различные величины и воздействия горячего воздуха в течение определенных промежутков времени.
2. Выявлено, что величины падения усилий по основе и утку камвольных тканей зависят от их структурных характеристик: волокнистого состава, плотности тканей по основе и утку, линейной плотности нитей основы и утка, причем у ткани с содержанием лайкры в утке величина падения усилия во время релаксации ткани наименьшая.
3. Определено оптимальное время воздействия горячего воздуха, при котором усилие по основе и утку максимально падает и замедляется, либо прекращается, что говорит об окончании релаксационного процесса в тканях.
4. Установлено, что при максимальных величинах деформирования ткани по основе и утку величины падения усилия соответственно при релаксации будут максимальны.

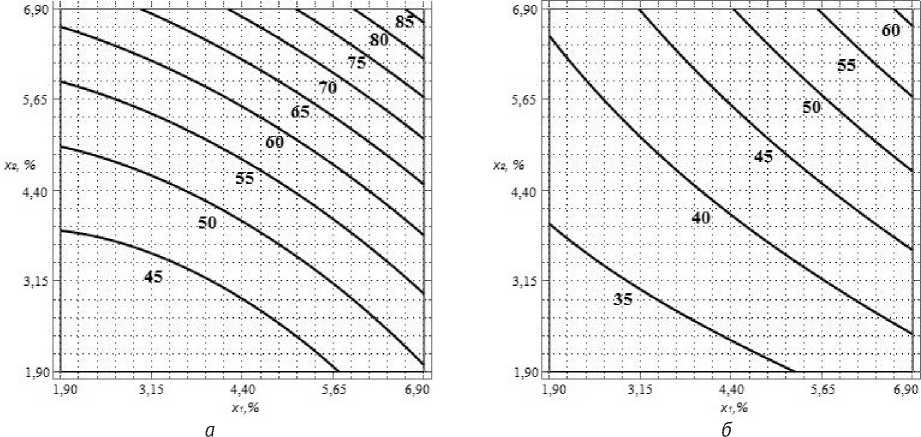
Рисунок 5 – Двумерные сечения поверхности отклика модели падения усилия по основе (а) и утку (б) в процессе релаксации ткани 3

Список литературы Разработка математических моделей для прогнозирования падения усилий по основе и утку полушерстяных камвольных тканей в процессе термофиксации

Денежкина, О. А., Иванцова, Т. М. (2005), Исследование термомеханических свойств шерстяных тканей с вложением нитей полиуретана, Известия ВУЗов. Технология текстильной промышленности, 2005, № 5 (286), С. 10-12.
Лисиенкова, Л. Н., Кирсанова, Е. А. (2010), Анализ деформационного состояния материалов для одежды в условиях пространственного растяжения, Известия ВУЗов. Технология текстильной промышленности, 2010, № 2 (323), С. 29-30.
Юферова, Л. В. (2002), Исследование формовочных способностей текстильных материалов, Сборник материалов международной научно - технической конференции "Современные наукоемкие технологии и перспективные материалы текстильной и легкой промышленности", Иваново: ИГТА, 2002.
Гапонова, Т. А., Садовский, В. В., Братченя, Л. О. (2020), Исследование релаксации усилий в полушерстяных камвольных тканях при двухосном растяжении, Минск, Вестник БГЭУ, 2020, № 3, С. 47-56.
Гайдарин, А. Н., Ефремова, С. А. (2008), Использование метода композиционного планирования эксперимента для описания технологических процессов. Методические указания, Волгоград, 16 с.

Статья научная