Разработка математических моделей системы «технологическое оборудование - груз» поворотного лесопогрузчика в режиме подтягивания груза

Расчетная схема системы “технологическое оборудование – груз” представлена на рисунке. Рассматриваемый режим может иметь место при работе манипулятора в качестве технологического оборудования лесопогрузчиков, валочно-трелевочных машин, машин для бесчокерной трелевки деревьев и других лесосечных и лесотранспортных машин.

После захвата груза рабочим органом он подтягивается к машине перемещением подвижных секций телескопической стрелы при помощи механизма выдвижения секций (МВС) и поворотом колонны относительно оси О. При этом стрела совершает сложное движение: секции стрелы совершают поступательное движение относительно оси Х и одновременно стрела совершает поворот относительно оси К и оси О. Полости гидроцилиндра подъема стрелы находятся в плавающем положении, что обеспечивает свободное перемещение груза по поверхности пути.

Данный режим позволяет сократить время цикла и повысить производительность поворотного лесопогрузчика. Однако следует учитывать, что при этом возникают динамические нагрузки, которые необходимо учитывать при проектировании.

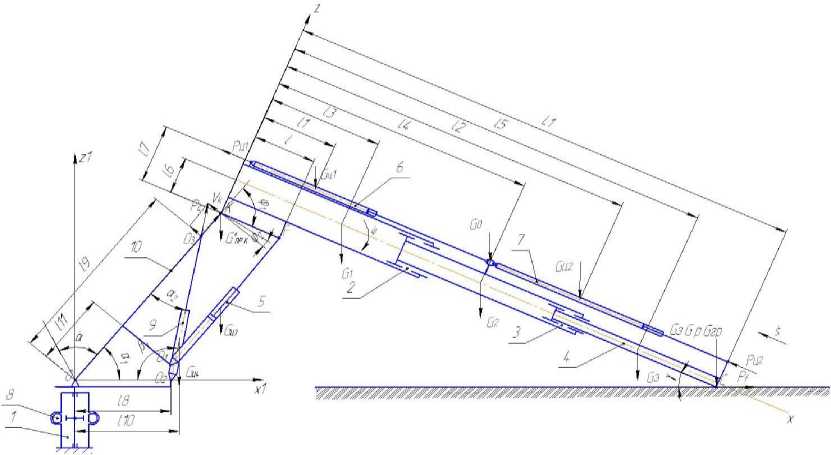
Расчетная схема системы “технологическое оборудование – груз” (манипулятор с отклоняющейся колонной); 1 – опорно-поворотное устройство; 2, 3, 4 – наружная, средняя, внутренняя секции телескопической стрелы; 5 – гидроцилиндр подъёма стрелы; 6, 7 – гидроцилиндры МВС; 8 – механизм поворота манипулятора в горизонтальной плоскости; 9 – гидроцилиндр поворота колонны; 10 – колонна

На рисунке приняты следующие обозначения: G 1 , G 2 , G 3 – силы тяжести наружной, средней и внутренней секций стрелы; G З , G гр , G р – силы тяжести захвата, груза и ротатора, приведенные в точку С – точку подвеса ротатора к стреле; G 0 – силы тяжести механизма изменения вылета, приведенные к центру массы средней секции; G Ц1 , G Ц2 – силы тяжести гидроцилиндров выдвижения секций стрелы. Принимаем G Ц1 = G Ц2 ; G Ц3 , G Ц4 – силы тяжести гидроцилиндров подъема стрелы и поворота колонны; G ПР.К – суммарная сила тяжести элементов конструкции колонны, приведенная к точке K; P С – усилие на штоке гидроцилиндра поворота колонны; P Ц1 , P Ц2 – усилия на штоках гидроцилиндров механизма изменения вылета, P Ц1 = P Ц2 ; P f – сила сопротивления перемещению дерева; L 1 – размер стрелы при выдвинутых секциях; l 1 , l 2 , l 3 , l 4 , l 5 – расстояния от оси вращения стрелы К до центров тяжести элементов конструкции; l, l 6 , l 7 , l 8 , l 9 , l 10 , l 11 – размеры элементов конструкции манипулятора; а - угол поворота колонны в плоскости Z 1 OX 1 ; а - угловая скорость вращения колонны; S - ход телескопического устройства стрелы; S - скорость поступательного движения секций; ф -угол поворота стрелы в плоскости ZKX; р - угловая скорость вращения стрелы; V k - скорость перемещения колонны; γ и γ 1 – вспомогательные углы.

Стрела совершает вращение с одновременным втягиванием секций в плоскости ZKX, колонна вращается в плоскости Z 1 OX 1 . Углы поворота α и φ, а также величина перемещения секций S, однозначно определяют положения данных элементов системы в плоскостях вращения. Исходя из этого, данную систему можно рассматривать как систему с тремя степенями свободы (K=3) с обобщенными координатами α,S и φ.

Для составления уравнений движения данной механической системы воспользуемся уравнениями Лагранжа 2-го рода. В соответствии с числом степеней свободы системы записываем три уравнения Лагранжа:

^d( ^{∂ T}) -^{∂ T} = Q ; ^d( ^{∂ T} ) -^{∂ T} = Q ; ^d( ^{∂ T} ) -^{∂ T} = Q α S ϕ

dt да да       dt дS   дS      dt др  др

где T – кинетическая энергия системы; Q α – обобщенная сила, соответствующая обобщенной координате α; Q s – обобщенная сила, соответствующая обобщенной координате S; Q φ – обобщенная сила, соответствующая обобщенной координате φ.

Кинетическая энергия рассматриваемой системы равна сумме кинетических энергий колонны, стрелы и груза:

T = T K + Т ГР + T C ,

где T K – кинетическая энергия приведенной к точке К массы колонны и элементов конструкции, смонтированных на ней (гидроцилиндров поворота колонны и подъема стрелы и других частей гидропривода); T ГР – кинетическая энергия груза, захвата и ротатора; T C – кинетическая энергия массы стрелы.

Кинетическая энергия колонны равна:

T = I O ® = ^т ПР. К ^L K ^a

.

K22

Получено выражение приведенной к точке К массы колонны и элементов конструкции:

l2

.

т_ПР к = 0,25 т_к + 0,125 т_{ц 3} •    + 0,125 т_{ц 4} • 4

.                     Ц  L2K          Ц

Подставив (4) в (3), получим выражение для определения кинетической энергии колонны:

(0,25 m_K + 0,125 m,_r, •    + 0,125 m,_{r 4} • 4) Lid²

K           Ц3   2           Ц4   2

=_________________ ^LK ___________ L K _____

.

K ₂

Так как захват, ротатор и груз перемещаются по поверхности погрузочной площадки, их кинетическая энергия равна:

_т _ (m p + m + mrpWk

ГР                2             , где VГС – скорость горизонтального перемещения масс mр, mз, mгр по поверхности погрузочной площадки.

Скорость V ГС величина переменная, напрямую зависящая от значения угла φ. Она определяется по следующим выражениям:

При у >  90 ° и / ₂ = у - 90 ° V rc = Vk cos( y + y 2 ) + Scos у .

Скорость перемещения колонны V K определяется из выражения:

Vk =a Lk .(8)

Таким образом, кинетическая энергия груза, захвата и ротатора для данного случая будет определяться из выражения:

_T _ ⁽ m p ^{+ т}з ^{+ т}гр )( ^a L K ^cos( Y ⁺ Y 2 ) ^{+ S cos} Y ^{) 2}

Trpi =                            2                            .

При ф<90° и y2 = 90°-ф Vrc = Vkcos(Y2 — Y) + ScosY•(10)

Для данного случая кинетическая энергия равна:

_T _ ( ^m _P + m 3 + m rp ^{)( a} L K cos( Y - у ) + S cos у )

^Т ГР2 =                          ,                            .                               ⁽¹¹⁾

Элементы конструкции стрелы движутся с постоянной скоростью V C , которая определяется из выражения:

V_ci = V2 + S ² + 2V_K:S cos y₂ = у/ ос ² L²_K + S ² + 2 a SL_K cos у₂

Кинетическая энергия системы в конце первого этапа определяется следующим выражением:

^Т 1 = |^{< P ²[⁽ m 3 r 5 ^{2 +} m

^₂ r ² + mr ² + mr ² + m^r ² + m^²) + ( m ₃ (- r₅S + 0,25 S ²) +

+ m_{4 2}(-0,5 r₂S + 0,0625 S ²)] + [ a² L ^( m ₃ + 0,5 m ^ ₂ + m ₂ + m ₀ + m_v j + m ) + S ²( m ₃ + 0,5 m ^ ₂) +

+ 2 aL_KS cos у ₂ ( m ₃ + 0,5 m ^₂)] + [( a ² L²_K cos² ( у + у ₂))( m_P + m₃ + m_rP) +

+ (2 aL_K cos(у + у ₂) S cos у )( m_p + m₃ + m_rp) + ( S ² cos² у )( m_p + m₃ + m_r p)] + [ m_npKL²_Ka ² ]}.

Кинетическая энергия системы в конце второго этапа определяется по выражению:

Т ₂ = ~{

2[(m1 ^гз + m_Ц 1 Г2 + m₂r₄²+ mоr₄²+ m₃^rs + m_Ц2r₂²) + (m_Ц 1(—0,5r1 S + 0,0625S²) +

+ m₂ (—r₄S + 0,25 S²) + m₀(-r₄S + 0,25 S²) + m₃ (-2 r₅S + S²) + m_{Ц 2} (-1,5 r₂S + 0,5625S²)] +

+ [a²L!(m, + m₉ + m, + 0,5 m_TT, + m_{rr 9} + m_n ) + S²(m-, + m. + 0,5 m_TT, + m_{rr 9} + m_n ) + L       KV 1       2       3      ,     Ц 1       Ц 2       0/         V 2       3      ,     Ц 1       Ц 2       0/

+ 2a L_KS cos у₂(m₂+ m₃+ 0,5m_Ц 1 + m_Ц2+ m₀)] + [(a²LK cos²(у₂— у))(m_p + m₃ + m_rP) +

+ (2a L_K cos(у₂— у) Si cos у)(m_p + m₃ + m_rp ) + (S²cos²у)(m р + m₃+ тгр )] + [тПР.К L²_Ka²]}

Для получения уравнений движения системы на первом и втором этапах производим дифференцирование выражений (13) и (14) по составляющим уравнений Лагранжа. Далее подставляем результаты дифференцирования кинетической энергии в левые части уравнений Лагранжа (1).

Так как гидроцилиндры подъема стрелы находятся в плавающем положении, то сила тяжести стрелы в любой момент времени распределяется между точками K и C. Составляющие силы тяжести стрелы: G^K – часть силы тяжести стрелы, передающаяся на колонну; G^C – часть силы тяжести стрелы, передающаяся на захват, ротатор и груз.

Точка приложения равнодействующей сил тяжести частей стрелы может быть определена из выражения, составленного на основании теоремы Вариньона:

£ Gili = GcLc ,(15)

где Gi – силы тяжести составных частей стрелы; l – координаты центров тяжести частей Gi относительно точки К; Gc - сила тяжести стрелы, равная сумме сил тяжести составных частей; L_c - координата центра тяжести стрелы относительно точки К.

LC = ^’l ■(16)

GC

Значение G^C определим из уравнения равновесия стрелы относительно точки К:

^Мк = 0 ; — GCLC — GCL = 0 ; GC = GCLC ■(17)

“L

Значение GK = G_c- GC.

Значения G^C и G^K величины переменные, зависящие от размеров L1 и L^', поэтому при моделировании режима движения стрелы с грузом их необходимо определять на каждом шаге варьирования факторов.

Сила сопротивления перемещению дерева, сил тяжести стрелы, захвата и ротатора:

Pf = (Gд + G3 + Grp + GCC) f.

На первом этапе движения стрелы обобщенная сила Q равна сумме проекций всех сил, совершающих работу в направлении обобщенной координаты S, то есть Q_sх= УF_sх.

Составляющая силы сопротивления Pf на первом этапе движения Pf1 на направление координаты S:

Pf 1S = Pf 1 cos y = (Gд + G3 + G_rp + GC ). f cos y.

Отсюда обобщенная сила, соответствующая обобщенной координате S для первого этапа 0 ≤ ΔS ≤ 0,5S, будет равна:

Qs 1 = У Psi = Рц 2 - [(0,5Gц 2 + G3 + Gp + G3 + Grp) • sin Y + Pf 1 ’ cos %].

Обобщенная сила Q в конце первого этапа движения равна сумме моментов всех сил относительно точки К, совершающих работу в данном направлении:

Q,1 = у MK = [-Gц2(12 -0,25S) - Gз(15 -0,5S) - (Gp + G3 + Grp)(L₁- 0,5S) -- G_o1₄- G₂1₄- G^ l, - G, l₃ ]cosy - P_f sin y(L, - 0,5S) - (Gy, + G_o + Gy₂)l₇ sin y + + (G, + G₂+ G₃+ G_p + G₃ + G_rp)16 sin y - Pf cosyl6.

Обобщенная сила Q равна сумме моментов всех сил, совершающих работу относительно оси вращения колонны:

^Qa1 = У ^MO = ^PC sin ^a2 ¹9  ^[(GC^{+ G}np. К ) ^LK^{cos a}1 ^{+ P}f^{cos y (L}K^{+ 1}6^)].

По аналогии получены обобщенные силы для второго этапа движения стрелы:

Qs2 = У Psi = Рц 1 - [(Gц2 + 0,5G^ 1 + G3 + G2 + G0 + Gp + G₃ + Grp) • sin y + Pf 2 • cos y].

Q_v2 = У Mk = [-Gц2( 12 - 0,75S) - Gз( 15 - S) - (Gp + G3 + G^)(L1 - S) - G₀( 14 - 0,5S) - G2 ( 14 - 0,5S) - Gy₁ (1, - 0,25S) - G1₃ ]cos y - P_f sin y(L, - S) - (в_ц, + G_o + Gy₂) 1, sin y +

+ (Gt + G₂ + G₃ + G_p + G₃ + G_r)11₆ sin y - P_f cos y1₆.

^Qa2 =У ^MO = ^PC sin «2 ¹9 ^{- [(G}C⁺G^p.К )^LK cos «1 ^{+ P}f cos у^(LK^{+ 1}6^)]’

Подставив выражения обобщенных сил Q_sj , Q_s2, Q^_x , Q₂, Q_a , Q_a2 в правые части уравнений Лагранжа (1), получим полные уравнения движения системы “рабочее оборудование – груз” для первого и второго этапов 0 ≤ ΔS ≤ 0,5S и 0,5S ≤ ΔS ≤ S.

Математическая модель движения системы “рабочее оборудование-груз” для первого этапа движения (0 ≤ ΔS ≤ 0,5S) имеет следующий вид:

|5(m₃+ 0,5m^₂) + a(m₃L_K cos y + 0,5mu^Lp cos Y) -

— a(m^L^ sin y • Y + 0,5m_rr-,L^ sin Y • Y) + 3 K      2   2         Ц2 K      2   2

+ a(im_pL_K cos(Y + Y ) cos Y + m.₃Lk cosY + Y ) cos Y + m._rL^k cos(Y + Y ) cos Y) — ^{— a(m}pLK^sin(y + Y₂⁾⁽Y⁺Y2)' ^cosY⁺ m3LK^sin(Y + Y₂⁾⁽Y + Y2)' ^cosY⁺

+ mrpLk sin(y + Y2)(Y + Y2)' cosY)— a(mpLk cos(y + Y2)sin Y' Y+

+ im₃L_K cos(Y + Y ) sin Y' Y + im_rL^K cos(Y + Y ) sin Y' Y) +

+ S(m_r cos²y + m3 cos²Y + mpp cos²Y) —

— 2S(m_r cos y sin Y ' Y + m3 cos y sin Y ' Y + mpp cos y sin Y ' Y)] —

— [m (m₃(—r + 0,5S) + m,,₂(—0,5r + 0,125S))] =

= РЦ2 — [(0,5G_Ц2 + G3 + G_P + G₃ + G_rP) ' sin Y + Pf 1 ' cos y] , ф[ m₃ (r₅²— r₅S + 0,25 S²) + m_{0 2}(r₂²—0,5 r₂S + 0,0625 S²) +

+ m₂r2 + m_or2 + myr²+ m^²] + m[m₃ (r₅S + 0,25 • 2S ' S) +

+ m₀₂(0,5r₂S + 0,0625 • 2S • S)] = [—G_o(ll₂ — 0,25S) — G₃(l₅ — 0,5S) —

— (Gd + Gq + G^d) (Li — 0,5S) — G0 14 — G2 14 — Gq 111 — G113 ] cos y —

— P_f sin y(Lr — 0,5S) — (G_oi + G_o + G_o)ll, sin y +

+ (Gi + G₂ + G₃ + G_B + G_e + G_a-)ll₆ sin y — P_f cos y1₆

[a( L 2 m₃ + L 20,5 m_L!2 + L 2 m₂ + L ²_K m^ + L 2 mp 1 + L 2 mi) +

+ S(m₃LK cos y₂+ 0,5m_Ц2LK cosy₂) — S(m₃LK sin y₂Y₂ + 0,5m_Ц2LK sin y₂Y₂) +

+ d(m Р L²Kcos²(Y + Y₂) + m₃L²Kcos²(Y + Y₂) + m_rPL²Kcos²(Y + Y₂)) -

^— 2d ⁽m p L²KCo^s(Y⁺Y 2)sin( Y⁺Y 2⁾⁽Y⁺Y 2)' ⁺

⁺m 3L²Kc^os(Y⁺Y 2^)sin(Y⁺Y 2⁾⁽Y⁺Y 2)' ⁺

⁺m _rpL²K^cos(Y⁺Y 2 ^)sin⁽Y⁺Y 2⁾⁽Y⁺Y 2)') ⁺

+ S(m_pL_Kcos(Y + Y₂)cosy + m₃L_Kcos(Y + Y )cosY + m_rPL_Kcos(Y + Y )cosY) —

— S(m_p L_Ksin( y + Y₂)(Y + Y₂)'cosY + m₃ L_Ksin( y + Y₂)(Y + Y₂)'cosY +

⁺m_ГрLKsin⁽y⁺Y2⁾⁽Y⁺Y2) ^cosY) ^—

— S(m_pL_Kcos(Y + Y₂ )sin yY + m₃L_KcosY + Y₂ )sin yY + m_rPL_Kcos(Y + Y )sin YY) +

+ dm_rlp„L² ] = P sin a, l„ — [(GK + G К_р „) L„ cos a + P_f cos y (L„ +1,)].

ПР.К K      C       2 9       C      ПР.К K       1     f          K    6

Математическая модель движения системы “рабочее оборудование – груз” для второго этапа движения (0,5S ≤ ΔS ≤ S) имеет следующий вид:

[S(m₂ + m₃ + 0,5m_L(3 + my₂ + m₀) + a(m₂L_K cos y + m₃L_K cos y +

+ 0,5my_XL_K cos y + my₂L_K cosy + m₀L_K cosy) — a(m₂L_K sin y ' Y₂ +

+ m₃L_K sin y ' Y₂ + 0,5myL_K sin y ' Y₂ + my₂L_K sin y ' Y₂ + m₀L_K sin y ' Y₂ ) +

+ a(m_pL_K cos(Y — Y)cosy + m₃L_K cos(Y — Y)cosy + m_rpL_K cos(Y — Y)cosy) —

— a(m_pL_K sin( y — Y)(Y — Y)' cosy + m₃L_K sin(y — Y)(Y — Y)' cosy +

+ m_PPL_K sin(y — Y)(Y — Y)' cos Y) — a(m_pL_K cos(Y — Y)sin Y ' Y' +

+ m₃L_K cos(Y — Y)sin Y ' Y + m_PPL_K cos(Y — Y)sin Y ' Y ) +

+ S (mp cos2 y + m3 cos2 y + mPp cos2 y) — 2S(mp cosysin y • y' + m3 cos ysin y • Y' + m2

+ m_PP cosysm y • Y )] — [^{my₃(—0,5r + 0,125S) + m₂(—r + 0,5S) +

+ m₀ (—r + 0,5 S) + m₃ (—2 r + 2 S) + my₂(—1,5 r₂ +1,125 S)}] =

= Pyj — [(Gy₂ + 0,5Gyj + G₃ + G₂ + G_o + G_P + G₃ + G_rP) • sin y + P_{f 2} • cos y]

^[mr²+ m₀((r²-0,5^S + 0,0625S2) + m₂(r₄²-r₄S + 0,25S²) +

+ m₀ (r₄²- r₄S + 0,25S²) + m₃ (r₅²- 2r₅S + S²) +

+ m₀₂ (r₂²-1,5r₂S + 0,5625S²)] +

0,

(0,5^S + 0,0625 • 2S • S) +

+m₂ (r₄S + 0,25 • 2S • S) + m₀ (r₄S + 0,25 • 2S • S) +

+ m₃(2r₅S + 2S • S) + m₀₂ (1,5r₂S + 0,5625 • 2S • S)] =

= [-Go2 (12 - 0,75S) - Gз( 15 - S) - (G_B + G_q + G_Ab) (L - S) -

• - G_o(l₄-0,5S) - G₂ (l₄- 0,5S) - G_B(lЦ - 0,25S) - G l₃]cosу -

• - P^ sin y(Lt - S) - (GBj + Go + GB 2)l7 sin у +

+ (Gt + G₂ + G₃ + G_B + G_Q + G_aJl₆ sin y - P_f cos yl₆

[a(L²m, + L2m₂ + LIm₃ + Lt0,5m  + L²m_rr2 + L2,m_n) + S(mL cosy + m₃L_p cosy +

K 1    K 2    K 3     K      Ц1    K Ц2    K 0         2 K      2    3 K      2

• + 0,5m_UtL_K cos y₂ + m_U2L_K cos y₂ + m₀L_K cos y₂) - S(m₂L_K sin y₂ • y₂ +

+m₃L_K sin y₂ • Y₂ +0,5m₄L_K sin у • y₂ + m_If2L_K sin у • y₂ + m₀L_K sin у • Y₂) +

+ d(m_PL2 cos²(y₂ - у) + m₃L2 cos²(y₂ - у) + m_rpL²_K cos²(y₂ - у)) -

• ^-2d⁽mpLK c^os(Y2 ^-y^)sin(y2 ^-Y⁾⁽Y2 ^-Y)' ^{+ m}3^LK ^cos(Y2 ^-Y^)sin(Y2 ^-Y⁾⁽Y2 ^-Y)' ⁺

+ mrpLK ^cos(Y2 ^-Y)^sin(Y2 ^-Y⁾⁽Y2 ^-Y)')^{+ S(m}PLK^cos(Y2 - Y^)cosY⁺

+m₃L_kcos(y₂ - Y)cosy + m_rpL_kcos(y₂ - Y)cosy) - S(m_PL_K sin(y₂- Y)(Y₂- Y) cos y +

+m3LK^sin⁽y2 ^-Y⁾⁽Y2 ^-Y)'^cosY⁺mrpLK^sin(Y2 ^-Y⁾⁽Y2 ^-Y)'^cosY)^-

-S(m_PL_Kcos(y - Y)sin Y• Y + m₃L_Kcos(y - Y)sin Y• Y +

= P_r sin a₂ L - [(GK + GК_Р )LL_p cos a, + P_f cos y (L_p + L)]. C       2 9       C      ПР.К   K       1     f           K    6

Заключение. В результате проделанной работы получены математические модели движения системы “технологическое оборудование – груз” поворотного лесопогрузчика в режиме подтягивания груза, позволяющие исследовать влияние на уровень динамических нагрузок на элементы конструкции конструктивных и эксплуатационных факторов (скорость поступательного движения секций, угловая скорость вращения стрелы, угловая скорость вращения колонны и т.д.).