Разработка математической модели асинхронного двигателя с фазным ротором в Comsol Multiphysics® для оценки энергетических параметров в стационарном режиме

На сегодняшний день многие технологические процессы зависят от качества и надёжности станков и других технологических устройств на базе электропривода (ЭП). Это создаёт необходимость в более качественном подборе элементов ЭП и систем их управления. В [1] рассматриваются основные критерии эффективности их работы. Наиболее важным критерием отмечается тепловое состояние элементов ЭП. При этом там же отмечается, что большинству критериев отвечает ЭП на базе двигателя двойного питания (ДДП).

В результате глубоких теоретических исследований ЭП с ДДП были синтезированы энергоэффективные алгоритмы управления [2]. Однако эффективность алгоритмов рассматривалась с учётом ряда допущений при синтезе математической модели двигателя. Кроме этого, оценка производилась без учёта его теплового состояния при заданных режимах работы. Для устранения данного пробела в исследованиях и подтверждения адекватности их результатов необходимо провести анализ теплового состояния двигателя при реализации энергоэффективных алгоритмов управления.

Большинство тепловых моделей двигателей синтезированы с помощью методов эквивалентных схем (МЭС) с сосредоточенными параметрами. Данные модели хорошо себя зарекомендовали для проведения оценки состояния двигателя за счёт простоты и возможности интеграции в системы защиты. Однако в связи с принимаемыми допущениями при их синтезе для ряда задач их адекватность ставится под сомнение. Наиболее интересными в рамках проводимых исследований являются модели, полученные с помощью метода конечных элементов (МКЭ) [3].

В МКЭ математическая модель строится на основе следующих компонентов: физическая модель, геометрическая модель, математическая модель и граничные условия для них. Таким образом, модели МКЭ можно использовать только для анализа исследуемого объекта или его полного аналога. Появление отклонений от исходного объекта в каком-либо из компонентов приведёт к результатам моделирования, не отвечающим требованиям оценки адекватности. Это приводит к дополнительным трудностям для исследователей, так как полученные результаты могут быть справедливы только для конкретной модели.

Тепловой анализ двигателя в целом является нетривиальной задачей. Модели МКЭ позволяют более точно произвести оценку. Однако программное обеспечение, позволяющее построение подобных моделей, производит тепловой расчёт с использованием начальных и граничных условий источников тепла. Получить необходимые параметры для теплового расчёта можно из электромагнитных моделей, полученных с помощью МЭС, как показано в [4], либо с помощью МКЭ, показанного в [5]. Это приводит к тому, что адекватность оценки теплового состояния двигателя будет определяться адекватностью электромагнитной модели.

В статье приводится разработка двухмерной электромагнитной модели асинхронного двигателя с фазным ротором (АДФР) 4AK160M4Y3 в программе COMSOL Multiphysics ^® . Предлагаемая модель будет использована в дальнейшем для оценки теплового состояния двигателя при реализации энергоэффективных алгоритмов управления.

Разработка геометрии модели

Паспортные данные АДФР 4AK160M4Y3 представлены в табл. 1. На их основе были произведены расчёты геометрии и электрических параметров двигателя по предлагаемой методике в [6]. Результаты расчётов необходимых параметров для построения модели представлены в табл. 2.

На основе расчётов была построена геометрическая модель с использованием стандартного функционала COMSOL, показанная на рис. 1. Учитывать изоляцию фазных обмоток и пазов двигателя в геометрии модели для электромагнитных расчётов нет необходимости. Данные параметры будут учтены в модификации геометрии для теплового расчёта.

Таблица 1

Паспортные данные двигателя 4AK160M4Y3

Table 1

Motor data sheet for 4AK160M4Y3

Количество фаз	3
Число пар полюсов	2
Номинальная мощность, кВт	14
Фазное напряжение статора ∆ / Y , В	220/380
Синхронная скорость вращения, об/мин	1500
Номинальное скольжение, %	3,7
Критическое скольжение, %	32,1
КПД, %	88,5
cosφ	0,87

Таблица 2

Результаты расчётов параметров двигателя 4AK160M4Y3

Table 2

Calculation results for the parameters of the 4AK160M4Y3 motor

Параметр	Статор	Ротор
Внешний/внутренний диаметр сердечника, мм	272/185	184/78,88
Длина сердечника, мм	180	180
Тип стали	2212	2212
Толщина листа стали	0,5	0,5
Односторонний воздушный зазор, мм	0,5	0,5
Число пазов	48	36
Число эффективных проводников	30	6+6
Число элементарных проводников	2	4
Число параллельных ветвей	2	1
Диаметр проводника, мм	1,4	1,4
Вид обмотки	Однослойная концентрическая	Двухслойная петлевая равносекционная
Шаг обмотки в зубцовых делениях	11;9	7
Вид пазов	Полузакрытый трапецеидальный	Полузакрытый глубокий
Высота паза, мм	18,5	26,3
Ширина шлица, мм	3,7	3,7
Высота клина, мм	1	1
Наибольшая ширина паза в штампе, мм	9,9	9
Наименьшая ширина паза в штампе, мм	7,3	4,5
Число витков в фазе	120	72
Фазный ток, А	27,55	45,84
Длина воздушного зазора, мм	119
Магнитный поток в воздушном зазоре, Вб	8,318∙10–3
Магнитная индукция в воздушном зазоре, Тл	0,755
Крутящий момент, Нм	102,43

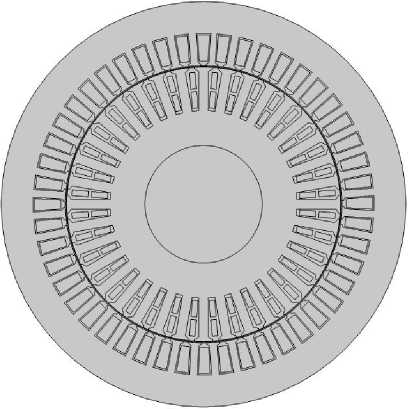
Рис. 1. Двухмерная геометрическая модель двигателя 4AK160M4Y3 Fig. 1. 2D geometric model of the 4AK160M4Y3 motor

Математическое описание модели

Электромагнитное поле в асинхронном двигателе описывается уравнениями Максвелла, имеющими вид:

divB = 0,(1)

где B – плотность магнитного потока;

rotE = -—,(2)

dt где E – электрическое поле;

rotH = J,(3)

где H – магнитное поле; J – плотность тока.

Совокупность уравнений (1)–(3) с определяющими соотношениями для свойств материалов даёт следующие уравнения, которые решаются в рамках физики вращающихся машин в COMSOL [7]:

dA    —_ — — о — + rotH - оv х B = J ;(4)

d t rotA = B,

где A – вектор магнитного потенциала; σ – электропроводность; v – скорость проводников; Je – плотность тока, создаваемая внешним источником.

Внешняя плотность тока для паза статора модели асинхронного двигателя с многовитковой обмоткой описывается как

NI

J e A e ,

где N – число витков в обмотке статора; I – фазный ток статора; A – общая площадь поперечного сечения обмотки; e – векторное поле, представляющее направление обмотки в пазу.

Ввиду того, что ротор в данном двигателе является фазным и многовитковым, приведённые формулы справедливы и для его описания.

Внутренний момент двигателя рассчитывается с помощью тензора напряжений Максвелла для двумерной модели по формуле

T = ^~(BBrBe dS9, (7) δμ0 Sδ где δ – толщина воздушного зазора; μ0 – магнитная проницаемость вакуума; r – радиус до точки, в которой плотность магнитного потока имеет радиальную компоненту Br и тангенциальную компоненту Bθ ; Sθ – поперечное сечение поверхности воздушного зазора.

Связь геометрии моделии параметров двигателя

Расчёт модели ведётся с учётом параметров и характеристик материалов для заданных областей, а также их расположения. Поэтому необходимо вводить параметры двигателя в модель точно согласно его конструкции. В табл. 3 приведено соответствие элемента модели двигателя с его материалом.

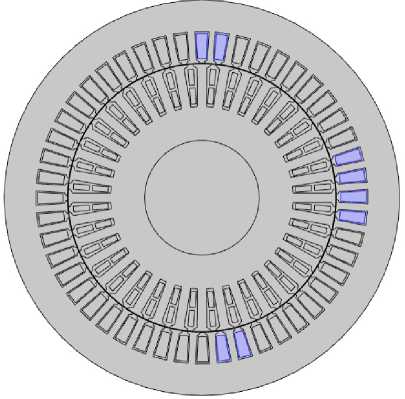
Фазные обмотки электрической машины играют важную роль в создании вращения. Правильное отображение обмоток также окажет влияние на результаты моделирования. Необходимо учесть тип обмотки, обмоточный шаг и параллельность её ветвей. На рис. 2 и 3 показаны обмотки статора и ротора для фаз А и U с учётом их параметров из

Таблица 3

Соотнесение материалов элементов двигателя 4AK160M4Y3 с геометрической моделью двигателя

Table 3

Assigning materials to the elements of the 4AK160M4Y3 motor geometric model

Обмотки фазы Воздушный зазор Сталь статора и ротора Вал

Copper Air Rusteel 2212 Structural steel

а)

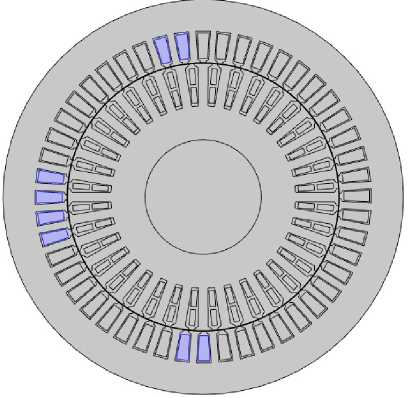
Рис. 2. Выбор областей в геометрической модели для обмотки статора фазы А : а – первая параллельная ветвь; b – вторая параллельная ветвь

Fig. 2. Selecting regions for stator phase A winding: a – first parallel branch; b – second parallel branch

b)

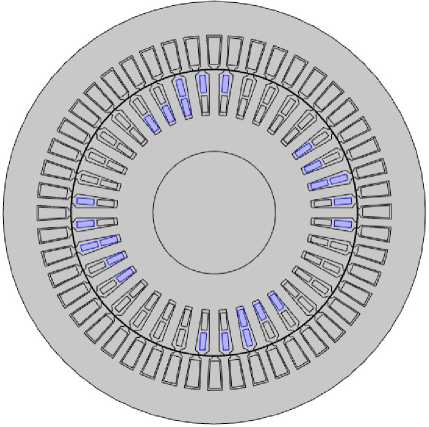
Рис. 3. Выбор областей в геометрической модели для обмотки ротора фазы U

Fig. 3. Selecting regions in the geometric model for the winding of phase U of the rotor

табл. 2. Для остальных фаз подобное отображение также справедливо с учётом их смещения на соответствующее полюсное деление.

Результаты моделирования

Моделирование проводилось для номинального режима работы двигателя со следующими параметрами:

• •    постоянная скорость вращения – 1440 об/мин;

• •    электрическая частота статора – 50 Гц;

• •    электрическая частота ротора – 5 Гц;

• •    фазный ток статора – 27,54 А;

• •    фазный ток ротора – 45,84 А.

На рис. 4 показано распределение плотности магнитного потока и магнитных линий. Согласно ему магнитное поле создаёт четыре магнитных полюса, что означает правильное расположение обмоток машины.

Одна из задач, решаемая переходом к МКЭ, – это учёт непостоянства и пульсаций магнитного потока в воздушном зазоре. На рис. 5 показано полученное распределение магнитного потока в воз-

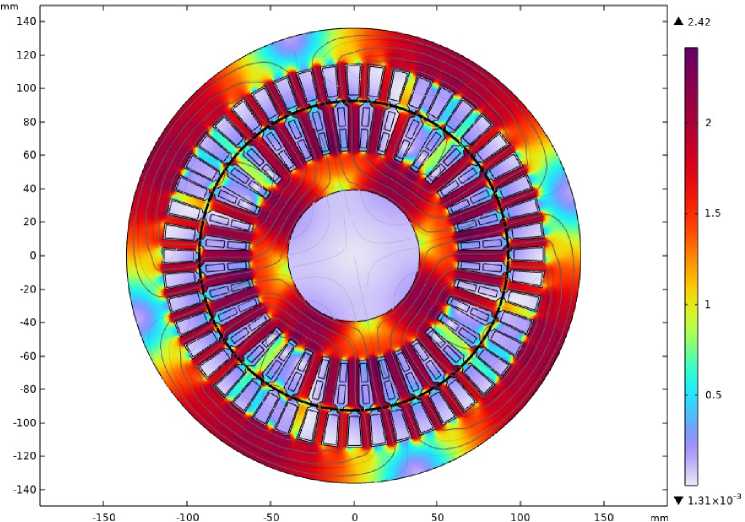
Рис. 4. Распределение плотности магнитного потока и магнитных линий в двигателе Fig. 4. Distribution of magnetic flux density and magnetic field lines in the motor

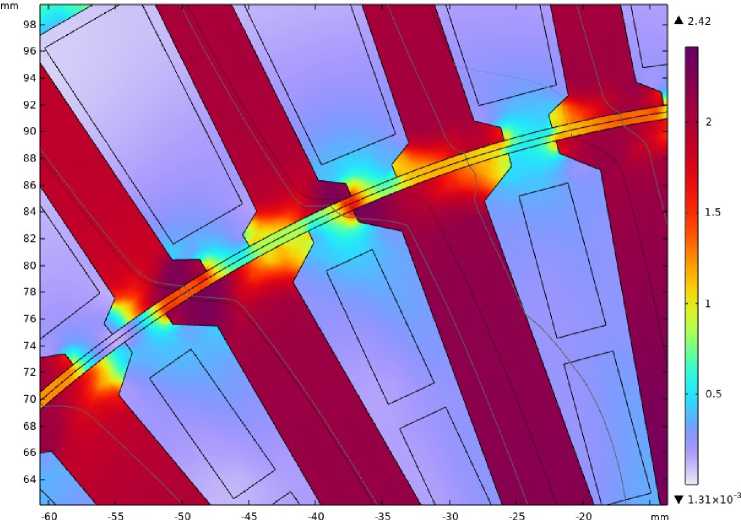
Рис. 5. Распределение магнитного потока в воздушном зазоре Fig. 5. Magnetic flux distribution in the air gap

Таблица 4

Сравнение результатов эксперимента и моделирования двигателя 4AK160M4Y3

Table 4

Comparison of experimental and simulation results for the 4AK160M4Y3 motor

Параметр Эксперимент Модель Погрешность, % Крутящий момент, Нм 101,91 99,71 2,21 Фазный ток статора, А 26,63 27,54 3,3 Фазный ток ротора, А 43,68 45,84 4,7 Линейное напряжение ротора, В 195,8 189 3,6 душном зазоре. Очевидно, что магнитный поток в полученной модели не является постоянным и его максимальное значение достигается в зубцовой зоне, что отвечает теории электрических машин.

В табл. 4 приведено сравнение электромагнитных параметров, полученных в ходе эксперимента и моделирования. Экспериментальный стенд включает в себя: АДФР 4AK160M4Y3, преобразователь частоты «ОМЕГА 55 ПЧ-ТТПТ-125-380-50-1УХЛ4», промышленный компьютер NI-PXI-1042Q [8]. Как видно из табл. 4, между значениями имеются незначительные различия.

Вывод

Модель трёхфазного асинхронного двигателя с фазным ротором была выполнена в COMSOL Multiphysics®. Для ускорения и упрощения расчётов было выбрано квазитрёхмерное построение модели. Полученные результаты имеют допустимую погрешность, что говорит об адекватности полученной модели. Данная модель будет использована для дальнейших исследований по оценке режимов работы двигателя в составе электропривода при реализации энергоэффективных законов управления.