Разработка математической модели динамики атмосферы и распространения вредных выбросов над г. Красноярском

ной системе уравнений Рейнольдса для слабосжимаемой среды с переменной температурой. Фазово-осредненные уравнения для переноса импульса (1), тепла (2) (в форме потенциальной температуры) и влаги (3) являются основой для модели на нестационарных уравнениях Рейнольдса (U-RANS):

Q _ Dt dxt " Pd>Xt + ^^‘(^^^   ^ref), (1) РСП _ axej (2) Dt --a---- , dxt D{H) d?hj (3) -- = Dt -----. dxt Так как в крупномасштабных атмосферных течениях влияние турбулентной диффузии на- много сильнее, чем молекулярной, то последней можно пренебречь.

Нестационарные уравнения (1-3) формулируются в форме разложения, в котором переменные Ф^^^ раскладываются на часть, отфильтрованную по времени (с периодом фильтра, пропорциональным шагу по времени), обозначенную угловыми скобками, и стохастическую часть. Уравнения замыкались через многопараметрическую модель, где для рейнольдсовых напряжений использовалась гипотеза турбулентной вязкости, а для турбулентного потока тепла использовалось дополнительное слагаемое с амплитудой пульсаций температуры. Применяли следующий вид для тензора рейнольдсовых напряжений т j и турбулентных потоков тепла ( т_в j ) и влаги ( т _h j ):

ашл ашаХ  2.^

^-П^Ь^^(4)

T9i = 0ut = -Сф^(ти^ + 5те,~ + ^^^

9X19X1

тм - nu,     сф <£> ^ту д^ + ^rhj д^ j,(ш где Vt = С^(к)2 /(f) - турбулентная вязкость; в — коэффициент теплового расширения.

Выражения (4)-(6) получены из точных уравнений для вторых моментов, с сохранением структуры всех источниковых членов. Отметим, что в отличие от температуры влажность представлялась как пассивная примесь, что отражено в отсутствие слагаемого с гравитацией в выражении (6). Величины в фигурных скобках имеют значение отфильтрованных по времени трехмерных полей, получаемых решением соответствующих эволюционных уравнений: для кинетической энергии турбулентности, ее скорости диссипации и квадрата пульсаций температуры.

В итоге, добавляя к системе (1)-(6) уравнения для кинетической энергии турбулентности, ее скорости диссипации и квадрата пульсаций температуры (трехпараметрическую модель к—е—92), получаем замкнутую систему дифференциальных уравнений [2].

Для дискретизации системы дифференциальных уравнений используется метод конечных объемов, реализованный для расчета на произвольных совмещенных неструктурированных расчетных сетках. Аппроксимация всех членов уравнений (нестационарных, конвективных, диффузионных) осуществляется схемами второго порядка точности. Взаимосвязь поля давле-– 1002 – ния и поля скорости происходит через процедуру расщепления Simple-C. Для решения системы алгебраических уравнений используется многосеточный метод.

Тестирование

Для тестирования математической модели рассмотрено несколько тестовых задач о свободной конвекции. Первая задача представляет собой задачу о развитии свободноконвективного течения в зазоре между цилиндрами. Внутри цилиндра радиусом 46,3 мм расположен другой цилиндр радиусом 17,8 мм. Пространство между цилиндрами заполнено воздухом. Стенки внутреннего цилиндра имеют постоянную температуру 100 ºС, стенки внешнего – 54 ºС. Система находится в поле сил тяжести, в результате в полости между цилиндрами формируется ламинарное конвективное течение. На рис. 1 изображена общая картина течения, распределение поля температуры и график температуры в сравнения с экспериментом.

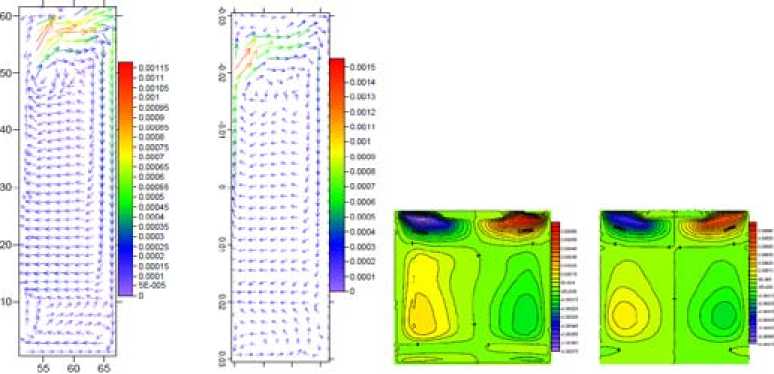
Вторая тестовая задача посвящена формированию турбулентного течения в замкнутой пространственной полости с нагреваемой стенкой. На рис. 2 представлены результаты сопоставления картины течения в камере с нагреваемой стенкой, полученные расчетом и экспериментально PIV-методом в ИТ СО РАН.

Результаты моделирования

Красноярск расположен по берегам реки и окружен предгорьем Саян и холмами. Для построения расчетной области брали геодезические данные. Для предварительного моделирования использовалась расчетная область размером 32x17x2 км, на которой строилась сетка, состоящая из около 5,6 млн узлов (рис. 3).

При задании граничных условий считалось, что река является источником влаги и имеет постоянную температуру ~ 0 ºC. Температура окружающей поверхности земли менялась со временем по синусоидальному закону, имитируя суточный цикл. Данные по суточной динамике температуры брали из осреднения данных городских метеостанций [3]. При моделировании учитывалось движение реки, полученное из предварительного 2D-расчета течения

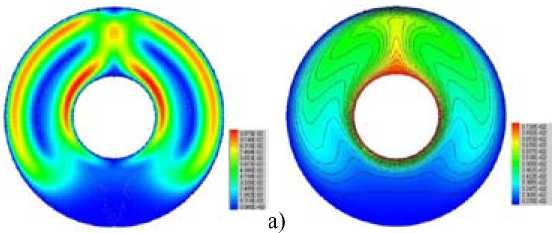
Рис. 1. Течение в зазоре между цилиндрами: а – модуль скорости; б – поле температуры; в – распределения температуры вдоль вертикальной линии над внутренним цилиндром

б)

Fig. 1. The flow in the gap between the cylinders: a – the velocity modulus; b – the temperature field; c – the temperature distribution along the vertical line above the inner cylinder

а)

б)

в)

г)

Рис. 2. Турбулентное течение в полости. Поле скорости в центральном сечении: а – численный расчет; б – PIV-измерение. Компонента скорости U: в – расчет; г – PIV-эксперимент

Fig. 2. Turbulent flow in the cavity. The velocity field in the central section: a – numerical calculation; b – PIV-measurement. Component of velocity U: c – calculation; d – PIV-experiment

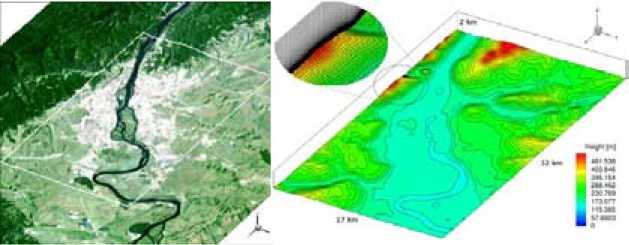
Рис. 3. Расчетная область атмосферы над г. Красноярском и расчетная сетка

Fig. 3. The calculated atmospheric region above the city of Krasnoyarsk and the calculated grid воды в реке. Основными источниками выбросов в атмосферу в городе выступают предприятия энергетики, металлургии и транспорт. Данные по температуре поверхности и источникам загрязнений основывались на анализе литературных источников и данных натурных измерений (рис. 4).

В результате расчета получаются данные о суточной динамике атмосферы над городом и распространении вредных примесей (рис. 5). Усредненные по времени (за сутки) поля концентрации примеси, полученные при моделировании, показаны на рис. 6.

Время расчета единичного варианта на одном процессоре класса Intel 7 составляет порядка 300 ч. В дальнейшем предполагается реализовать модель для параллельных расчетов на высокопроизводительной кластерной системе, что позволит выполнять моделирование в режиме реального времени.

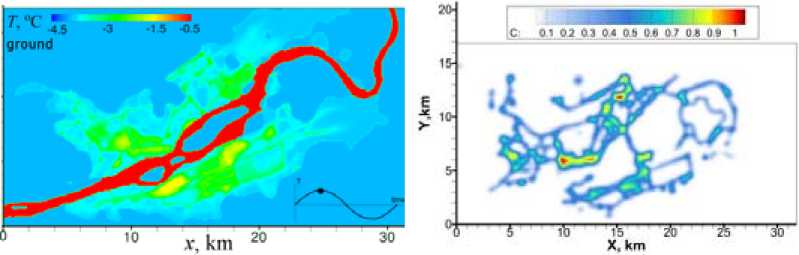
а)                                                            б)

Рис. 4. Характерные распределения: а – температуры вблизи поверхности земли в ноябре; б – источники загрязнений

• Fig. 4.    Characteristic distributions: a – temperatures near the surface of the earth in November; b – sources of pollution

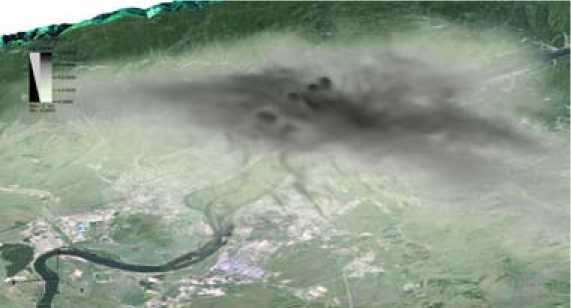
Рис. 5. Результат модельного расчета распространения вредностей над г. Красноярском

• Fig. 5.    The result of calculation of the spread of hazards over the city of Krasnoyarsk

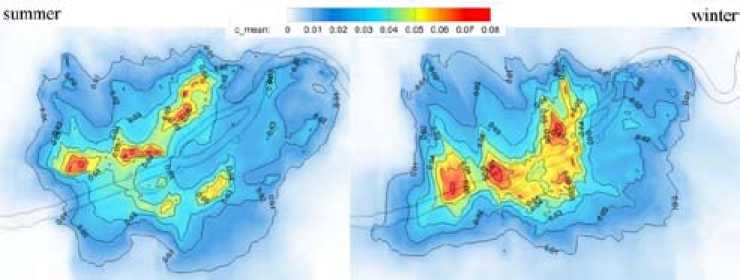
summer winter

Рис. 6. Расчетные усредненные концентрации загрязняющих веществ на высоте 50 м над землей. Левый рисунок – в летний период, правый – в зимний

• Fig. 6.    Average concentrations of pollutants at a height of 50 m above ground. The left drawing is in summer, the right one in winter

Заключение

В статье представлена математическая модель динамики атмосферы и распространения загрязнений над г. Красноярском. Приведены результаты тестирования модели и предварительные результаты расчетных исследований. Показана необходимость развития модели для возможности ее использования на высокопроизводительных кластерных системах с целью проведения расчетов в реальном режиме времени.

Исследование выполнено при финансовой поддержке РФФИ, Правительства Красноярского края, Красноярского краевого фонда поддержки научной и научно-технической деятельности в рамках научных проектов № 16-41-240788 р_а и 16-41-242156 р_офи_м.