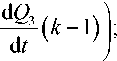Разработка математической модели пневматической системы термостабилизации

В статье представлен метод расчета пневмоэлектрического устройства для проведения полимеразной цепной реакции деления молекулы ДНК — пневматического амплификатора. Особенностями данной системы являются высокие скорости изменения температуры рабочего тела — воздуха при одновременном обеспечении точности изменения температуры биологического образца в пластиковой микропробирке. Целью исследований является моделирование тепловых процессов для создания оптимальных условий для проведения реакции деления молекулы ДНК. Представлена математическая модель расчета, основанная на методе сосредоточенных параметров. Описан экспериментальный стенд. Приведены результаты расчетнотеоретических исследований и их сравнение с результатами экспериментальных исследований. Показано, что предложенный метод позволяет оценить масштабы переходных процессов, протекающих в пневматическом амплификаторе. Сделан вывод о необходимости разработки математической модели, основанной на методах описания систем с распределенными параметрами.

ВВЕДЕНИЕ                     Возможны самые различные варианты реализа ции конструктивной схемы с точки зрения приме-

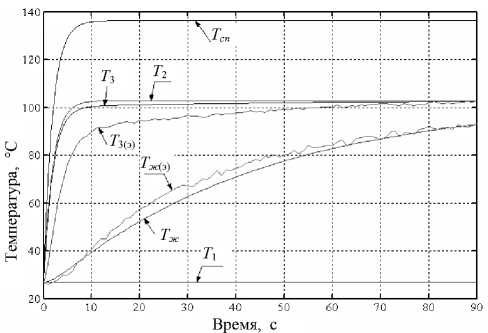
В современной технике широко применяются системы термостабилизации, предназначенные для поддержания определенной температуры объекта с заданной точностью. В настоящее время появился новый класс технических задач, в которых термостатирующие устройства не только поддерживают заданную температуру объекта но изменяют ее по заданной программе с требуемой скоростью и точностью. Данные устройства применяются в приборостроении, электровакуумной технике, медицине и т. д. По роду используемого рабочего тела, предназначенного для подвода и отвода тепла от объекта теплового воздействия, термостабилизирующие устройства могут быть: твердотельными; жидкостными и газовыми (пневматическими). В данной статье рассматривается вопрос разработки математической модели пневматической системы на примере термостатирующего устройства медицинского назначения. К таким устройствам относятся так называемые ам-плификаторы ДНК [1–3], в которых температура исследуемого образца должна изменяться циклически с высокой точностью и по программе, задаваемой пользователем. В основе большинства выпускаемых сегодня амплификаторв ДНК заложена твердотельная схема [4], но в связи с тем, что к этим устройствам сегодня предъявляется очень сложное требование — повысить скорость изменения температуры исследуемого образа до 10 ºС/с и выше, разработчики данного оборудования обратили внимание на пневматическую систему термостабилизации [5].

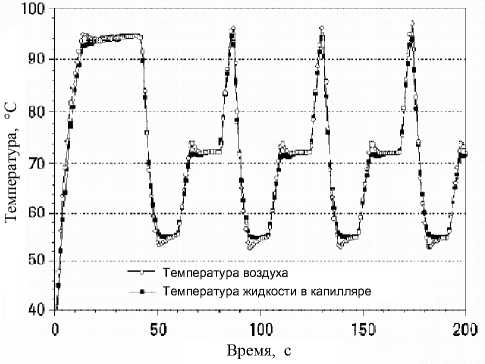
няемого газа. Но наиболее высокие потребительские свойства будут иметь конструкции, в которых в качестве рабочего тела используется воздух из окружающей среды и без предварительной подготовки. В устройствах данного типа побудитель расхода обеспечивает перемещение рабочего тела через преобразователь энергии, в котором происходит подвод тепла, и затем оно вступает в тепловой контакт с объектом теплового воздействия для его нагрева. Для охлаждения объекта происходит замещение горячего воздуха холодным.

Разработка математической модели пневматической системы термостабилизации проводилась на примере системы для изменения и термостабилизации температуры жидкости, размещенной в стандартной, тонкостенной пластиковой микропробирке.

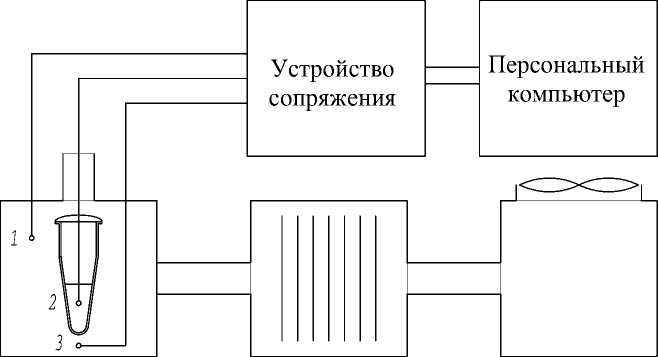
Расчетная термодинамическая схема данной установки приведена на рис. 1. Система состоит из набора условных проточных пневматических емкостей, разделенных между собой и отделенных от подводящих и отводящих магистралей условными дросселями. На входе в первую емкость установлен побудитель расхода (вентилятор), во второй емкости расположен преобразователь энергии — проволочный электронагреватель, а в третьей емкости размещается микропробирка с исследуемым образцом.

С позиции классической термодинамики рассматриваемое устройство представляет собой открытую термодинамическую систему [6, 7], границы которой проницаемы как для потока вещества,

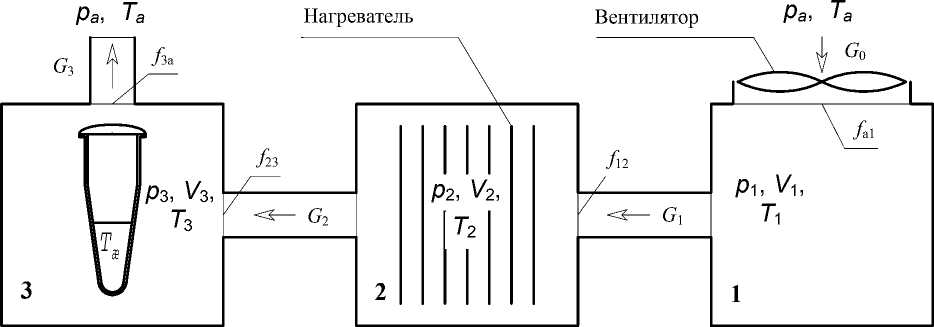
Рис. 1. Расчетная схема пневматической системы термостабилизации.

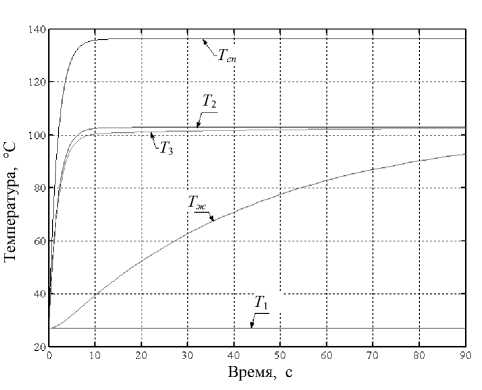
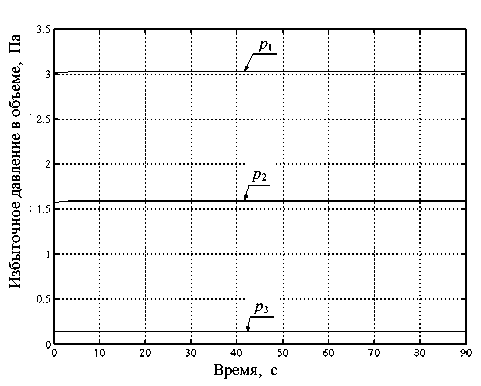
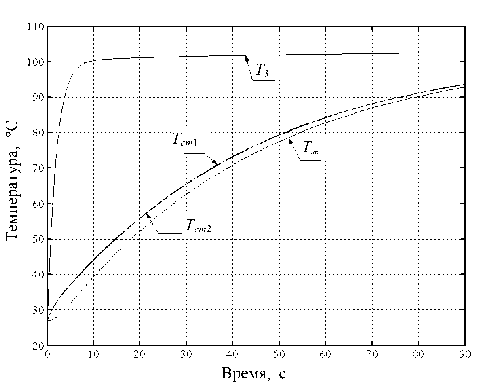
1 — первая (входная) емкость с вентилятором, с параметрами воздуха: давлением p ₁ , объемом V ₁ , температурой T 1 ; 2 — вторая емкость (преобразователь) с электронагревателем, с параметрами p 2 , V 2 , T 2 ; 3 — третья емкость с микропробиркой и образцом в ней (жидкость) с температурой T ж , с параметрами p 3 , V 3 , T 3 ; G 0–3 — потоки воздуха; p а , T а — параметры атмосферы; f a1 , f 12 , f 23 , f 3a — дроссели

так и для теплового взаимодействия. В представленной системе протекают процессы различной физической природы: термо- и газодинамические, теплопереноса и преобразования электрической энергии в тепло. Математическое описание данных процессов может быть основано на использовании системы уравнений в частных производных (при учете распределенных параметров) или обыкновенных дифференциальных уравнений, что возможно только при описании системы с сосредоточенными параметрами. Модель с сосредоточенными параметрами применима в случае квазиста-тических процессов. Известно, что изменение состояния можно рассматривать как квазистатиче-ское, если скорости протекания рабочих процессов тела малы по сравнению со скоростью распространения звука в газе при данных условиях [6]. При решении данной задачи изменения состояний можно с допустимой погрешностью считать ква-зистатическими, поскольку скорость потока рабочего тела и темпы изменения параметров системы как минимум на два порядка меньше указанной скорости звука. Система с распределенными параметрами по своей сущности ближе к реальным физически процессам и наиболее полно и точно описывает переходные процессы, протекающие в конкретных физических устройствах. Однако трудоемкость написания математических моделей и программ расчета данных систем, как правило, существенно превосходят трудоемкость для систем с сосредоточенными параметрами. Учитывая данный фактор, а также приемлемую точность расчетов с применением модели с сосредоточен- ными параметрами, рабочие процессы, протекающие в пневматической системе термостабилизации, описаны системой обыкновенных дифференциальных уравнений.

ОСНОВНЫЕ ЗАВИСИМОСТИ, ИСПОЛЬЗУЕМЫЕ ДЛЯ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ПНЕВМАТИЧЕСКОЙ СИСТЕМЕ

ТЕРМОСТАБИЛИЗАЦИИ

Зависимости для расчета изменения давления и температуры газа в открытой термодинамической системе при условии наличия теплообмена между рабочим телом и окружающей средой (рассчитываемая модель графически представлена рис. 2) описываются уравнениями [6, 7]:

dp dt

= kf RTnpGnp - RTG - pdV + dQ(k -1)1, (1) V l пр пр ух ух г d t     d tI dTT

--=X dtpV xf pdV+Vdp -RT(G.p - Gyx)+ dQ(k -1)), (2) ttt где p — давление газа, Па; T — температура газа, К; V — объем газа, м3; k — показатель адиабаты; R — газовая постоянная, Дж/(кг-К); G.p — массовый расход приходящего газа, кг/с; Gyx — массовый расход уходящего газа, кг/с; Q — количество теплоты, подводимое к газу, Дж.

Зависимость для определения расхода газа в условном дросселе, соединяющем соседние емкости системы, (модель на рис. 3) для докритиче-ского режима течения [7]:

G = f Ц Р 1

2 k 1

k - 1 RT

Р 2 A k

Р 1 ,

k + 1

Р 2 A k Р 1 ,

при Р кр < — <  1, p ₁

где f — площадь поперечного сечения в условном дросселе, м ² ; ц — коэффициент расхода; p ₁ — давление газа в емкости, из которой вытекает газ, Па; p ₂ — давление газа в емкости, в которую поступает газ, Па; T ₁ — температура газа

dQ

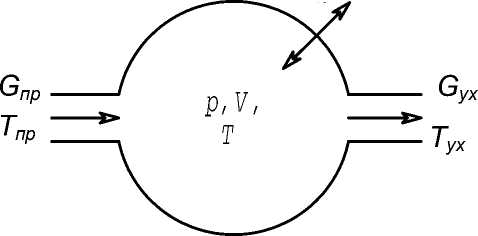
Рис. 2. Рассчитываемая модель открытой термодинамической системы при условии наличия теплообмена между рабочим телом и окружающей

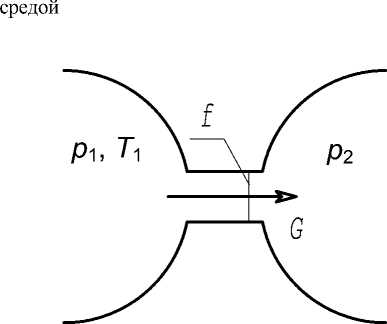
Рис. 3. Рассчитываемая модель соединения соседних емкостей системы через условный дроссель в емкости, из которой вытекает газ, К.

Зависимость для определения расхода газа в условном дросселе, соединяющем соседние емкости системы, для сверхкритического режима течения [7]:

G = f Ц Р 1

k + 1

k ( 2 A k - 1

RT₁ ( k + 1 J

при 0 <  p ² <  в . (4) p ₁

В пневматической системе термостабилизации вентилятор обеспечивает прокачку рабочего тела через электрический нагреватель, состоящий из нихромовой нити, подключенной к источнику тока.

Рассмотрим процесс передачи теплоты от электрического нагревателя к рабочему телу. Тепловой баланс электрического нагревателя (без учета теплообмена излучением):

Q = Q + Q ,             (5)

эл    СПсп    кОнвнв , где Qэл — количество теплоты, выделяемое в электрическом нагревателе, Дж; Qcп — количество теплоты, расходуемое на нагрев спирали, Дж; QK0He — количество теплоты, затрачиваемое на нагрев рабочего тела через конвективный теплообмен, Дж.

Количество теплоты, выделяемое в электрическом нагревателе:

Q = U . I. t = 12 . R . t =--t = P. t, эл

где P — мощность, прикладываемая к спирали, Вт; U — напряжение, прикладываемое к спирали, В; I — ток, протекаемый по спирали, А; t — время, с.

Количество теплоты, расходуемое на нагрев спирали:

Q = с -т -NT ,              (7)

сп сп сп сп , где СсП — теплоемкость материала спирали, Дж/(кг-К); тсп — масса спарили, кг; АТсп — разность между конечной и начальной температурой спирали, К.

Количество теплоты, затрачиваемое на нагрев рабочего тела через конвективный теплообмен [10]:

Q kohb = а • S • ( Т сп - T 2 ) • t               (8)

где а — коэффициент теплоотдачи, Вт/(м ²- К); S — площадь поверхности теплообмена, м ² ; Т сп — температура спирали, К; T ₂ — температура газа, К.

Дифференцирование приведенных выше зависимостей по времени дает

d Q эл	= d Q с n + d Q kohb .	d^ ЭЛ. = р ;
d t	d t d t	d t		(9)
d Q сп d t	d T = с сп ■ т сп ■ -; d t	d QKOHB _    ■ /т d t сп	- Т 2 ) •

Дифференциальное уравнение изменения температуры спирали:

d T„ _ P - aS ( T en — T 2 ) d/ cm сп сп

Рассмотрим процесс передачи теплоты от рабочего тела к жидкости, находящейся в пробирке. Пробирка рассматривается как тело цилиндрической формы, направление оси которого совпадает с направлением потока. Процесс переноса теплоты от рабочего газа к жидкости через разделяющую их стенку пробирки (рис. 4) включает в себя [11]:

• •    передачу теплоты от рабочего тела с температурой T ₃ к внешней стенке пробирки с температурой T_{ст 1} путем конвективного теплообмена

Т з - Т ст 1 = Ql ( « 1 • S ) = Q • R a ;         (11)

• •    передачу теплоты от внешней стенки пробирки с температурой T_{ст 1} к внутренней стенке пробирки с температурой T_{ст 2} путем теплопроводности

Тст 1 - Тст 2 = Q ■ Rx;(12)

• •    передачу теплоты от внутренней стенки пробирки с температурой T_{ст 2} к жидкости с температурой T_ж путем конвективного теплообмена

Тст 2 - Тж = Ql («2 ■ S2 ) = Q ■ R« 2.(13)

При стационарном режиме тепловой поток Q во всех трех процессах одинаков и равен

Q _   Тз — Тж_

• R « 1 + R x + R « 2

• ₌______________ Т з - Тж _______________

11 d ₁    1 ^, (14)

1 In +

• a1 ■ n ■ d 1 ■ 11 2 ■ n ■ X ■ 11 d 2 a 2 ■ n ■ d2 ■ 12

где R _{a 1} — термическое сопротивление теплоотдачи от рабочего тела к внешней стенке пробирки, Вт/К; R _x — термическое сопротивление теплопроводности от внешней стенки пробирки к внутренней стенке пробирки, Вт/К; R _{a 2} — термическое сопротивление теплоотдачи от внутренней

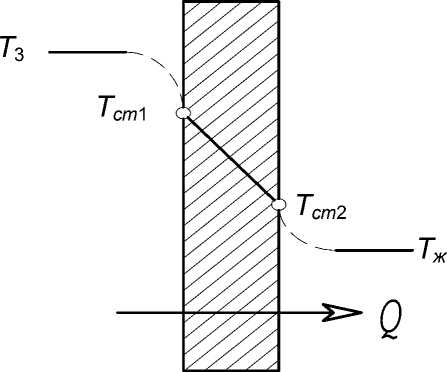
Рис. 4 . К расчету переноса теплоты от рабочего газа к жидкости в пробирке через разделяющую их стенку пробирки

стенки пробирки к жидкости, Вт/К; а , — коэффициент теплоотдачи от рабочего тела к внешней стенке пробирки, Вт/(м ² -К); а ₂ — коэффициент теплоотдачи от внутренней стенки пробирки к жидкости, Вт/(м ² -К); X — коэффициент теплопроводности материала пробирки Вт/(мּК); d ₁ — внешний диаметр пробирки, м; d ₂ — внутренний диаметр пробирки, м; l ₁ — длина пробирки, м; l ₂ — высота жидкости в пробирке, м.

Температура на внешней стенке пробирки T_{ст 1} и температура на внутренней стенке пробирки T_{ст 2} определяются по следующим зависимостям:

Т ст 1 = Т з - Q ■ R « 1 , Т ст 2 = Т ст 1 - Q ■ R x . (15)

Задача о нахождении теплового потока Q и температур стенок пробирки T_{ст 1} и T_{ст 2} решается методом последовательных приближений. Вначале для расчета значений а 1 и а ₂ приходится задаваться температурами поверхностей пробирки из условия Т ₃ >  Т_ст 1 >  Т_{ст 2} >  Т ж . Затем рассчитывается тепловой поток через цилиндрическую стенку пробирки по зависимости (14) и уточняются значения температур поверхностей стенок пробирки по зависимостям (15).

Наиболее проблематичной в предложенной постановке решения задачи является определение теплового контакта между преобразователем энергии и рабочим телом, а именно коэффициента теплоотдачи между нагревательным элементом и потоком воздуха. Несмотря на то что данный вопрос

а

б

в

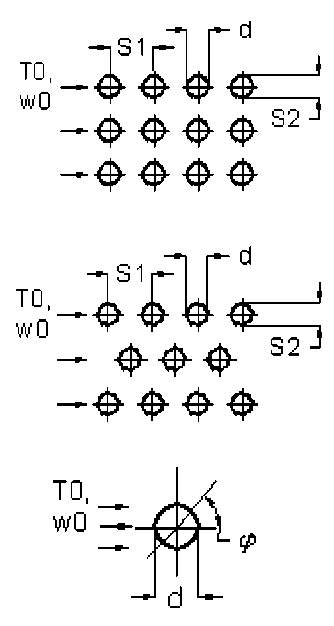
Рис. 5. К расчету обтекания системы цилиндрических тел (ЦТ) [12].

а — коридорный пучок ЦТ; б — шахматный пучок ЦТ; в — цилиндр, обтекаемый под углом атаки φ . Воспроизводится по [12]

достаточно хорошо изучен и освещен в технической литературе, моделирование процесса теплообмена при решении сопряженной задачи остается достаточно сложной проблемой, требующей экспериментальных исследований в каждом конкретном случае.

Обычно при решении большого класса задач коэффициент теплоотдачи между нагревательным элементом и потоком газа определяется через число Нуссельта:

a • d                       Nu • X

Nu =---- и, следовательно, a =-----, (16)

X                                d ' '

где d — характерный определяющий размер, м; X — коэффициент теплопроводности газа Вт/(мּК).

Расчетные зависимости или численные значения числа Нуссельта широко представлены в технической литературе по тепломассообмену. Обычно это экспериментальные данные, полученные для решения различных случаев обтекания твердых тел рабочим телом. Аналог, близкий ре- шаемым задачам — обтеканию электрического нагревателя, представляющего собой пучок тел цилиндрической формы, и обтеканию пробирки, представляющей собой цилиндрическое тело, — имеется в работах [6, 7, 9–13].

В работе [12] приводятся зависимости для определения числа Нуссельта для случая обтекания тел цилиндрической формы, в которых определяющим размером является диаметр цилиндра. Ниже приводим их, геометрия модели дана на рис. 5.

Коридорный пучок цилиндрических тел (рис. 5, а):

NU = 1.2Re^{0 33} • Pr/Pr4 Г5 при

l /Prc J sy^ < 1.25, s2d < 1.25, 10 < Re < 150;

Nu = 0,26Re0.65 • Pr033 • f d

0.15

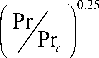
при

1.24 <  s/ d

< 4, 1.24 <  s ²/ < 4, 10 3 <  Re <  10 ⁵ d

Nu = 0.02Re ^0.84 • Pr ^0.36 •( ^Pr4

l / ^Pr c

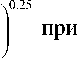
(18) ;

1.3 d

< 2.5,

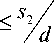
< 2.3,

10 ⁵ < Re < 10 ⁶ , 0.7 < Pr < 500.

Шахматный пучок цилиндрических тел (рис. 5, б):

Ж = 1.8Re ⁰³³ • Pr ⁰³³/ ^P% Г при

Pr l Z cJ                       (20)

sd <  1.25; s 2 d <  1.25, 10 <  Re <  200;

Nu = 0.41 Re ^0.6 • Pr ^0.33 •f Pr    ) • E s при

l rc J

• 1.3 <  s i/ <  2.6, 0.6 <  s 2/ <  4, d ^, d ^,

0.25

103

E_s = 1.12 при sV > 2;

s₂

Nu = 0.021 Re^0.84• Pr^0.36•[ ^Pr4 I при l /^Prc J

1.2 < sV,< d

2.5, 0.9 < s2d< 1.5, 10⁵< Re < 10⁶.

Обтекание цилиндра (рис. 5, в):

Nu = 0.5Re0.5 - Pr^0.38 -^fP% ) при I /Prc I ^F

5 < Re < 10³;

0.25

Nu = 0.026Re0.6- Pr^0.38-I ^Pr£ I при I /Prc I ^F

10³< Re < 2-10⁵;

0,25

Nu = 0,023 Re⁰’⁸- Pr^0,37-1 PrZ I при

I r I

3 -105 < Re < 2 -106.

В предварительно турбулезированном потоке, который соответствует рассматриваемому устройству (за вентилятором — побудителем расхода), теплоотдача на 50–60 % выше расчетной [12]. Если угол φ между направлением потока и осью цилиндра (угол атаки) меньше 90°, значение коэффициента а следует умножить на поправочный коэффициент

Еф = 1 - 0.54 - cos2 ф .(26)

В работе [13] для расчета теплоотдачи тела цилиндрической формы потоком воздуха приводятся следующие зависимости:

Nu = 0.49Re0.5 при 103 < Re < 2 -105;(27)

NU = 0.0245 Re0.6 при Re > 103.(28)

В работе [13] для расчета теплоотдачи проволочного нагревателя используется обобщенная формула

Nu = c -(Gr- Pr)n, где:

c = 0.5, n = 0 при (Gr-Pr) = 1-10-4...1-10-3, c = 0.5, n = 18 при (Gr- Pr) = 1 -10-3...5 -102, c = 0.54 , n = 14 при (Gr- Pr) = 5 -102...2 -107, c = 0.135, n = 13 при (Gr-Pr) = 2-107...1-1013.

Обработка экспериментальных данных по обтеканию тела цилиндрической формы потоком воздуха, полученных из различных источников, позволила автору работы [12] предложить следующую приближенную расчетную формулу:

где nb, n_w — коэффициент вязкости при средней и текущей температуре потока соответственно.

Анализ приведенных выше зависимостей для определения коэффициентов теплоотдачи позволил выбрать зависимости, наиболее полно описывающие процесс теплоотдачи между нагревательным элементом и рабочим телом, а также процесс теплоотдачи между рабочим телом и пробиркой.

Коэффициент теплоотдачи между нагревательным элементом и потоком газа определяется по следующей зависимости:

Nu ж - X а =----- d

где Nuж — значение числа Нуссельта; X — коэффициент теплопроводности газа при определяющей температуре, Вт/(м-К); d — диаметр проволоки спирали, м.

Определяющим размером является диаметр проволоки спирали. Определяющей температурой является температура T = (Т₂+ Т_сп)/2 (Т₂ — средняя массовая температура газа, К; T_сп — температура спирали, К).

Число Нуссельта определяется по критериальной зависимости для поперечного обтекания пучка тел цилиндрической формы, расположенных в шахматном порядке [10]:

Nuж = 0.41 - Re ⁰⁶- PrJ.3³-e_s;   Re,, = —;

жжs   ж

v

^£s =(^s1 I^s2)^1/6при ^s1 I^s2<2;                     ⁽³²⁾

Es = 1.12        при s1 /s2 > 2, где w — средняя скорость газа в самом узком сечении пучка, вычисленная при определяющей температуре, м/с; Prж — значение числа Прандтля для газа при определяющей температуре; Prс — значение числа Прандтля для газа при температуре спирали; v — кинематический коэффициент вязкости газа при определяющей температуре, м2/с;

Коэффициент теплоотдачи между потоком газа и пробиркой определяется по следующей зависимости:

Nu ж - X

Nu = ^0.4 - Re0.5 + 0.06 Re23) - Pr0.4 - при ;< Re< 105, 0.7 < Pr< 300I

Пь

Vw

0.25

где Nuж — значение числа Нуссельта; X — коэффициент теплопроводности газа при определяющий температуре, Вт/(м-К); d₁ — наружный диаметр пробирки, м.

Определяющим размером является наружный диаметр пробирки. Определяющей температурой является температура Т = (Т₃ + Тпр 1)/2 (Т₃ — средняя массовая температура газа, К; T_пр1 — температура внешней стенки пробирки, К).

Число Нуссельта определяется по критериальной зависимости для поперечного обтекания одиночной цилиндрической трубы [11]:

Nu ж = (0.43 + 0.55 • Re0/ • Pr/³⁸)• ^; ^ж.        ^ж.

w • d_x

Re. =-----1,

ж

v

где w — средняя скорость газа, вычисленная при определяющей температуре, м/с; Pr_ж — значение числа Прандтля для газа при определяющей температуре; v — коэффициент кинематической вязкости газа при определяющей температуре, м²/с; е_ф = 0.5 — коэффициент учитывающий угол между направлением течения потока и осью трубы.

Коэффициент теплоотдачи между пробиркой и жидкостью определяется по следующей зависимости:

а₂=

Nu ж • X

d₂

где Nu ж — значение числа Нуссельта; X — коэффициент теплопроводности газа при определяющей температуре, Вт/(м^К); d₂ — внутренний диаметр пробирки, м.

Определяющим размером является внутренний диаметр пробирки. Определяющей температурой является температура Т = (Тж + Т_пр2)/2 (Тж — средняя температура жидкости, К; T_пр2 — температура внутренней стенки пробирки, К).

Число Нуссельта определяется по критериальной зависимости для естественной конвекции [9]:

Nu ж = 1.18 -(Gr- Pr )^V8;

g • в •( Тст 2 - Тж )• d2            ⁽³⁶⁾

, v2

где Gr — значение числа Грасгофа; Pr — значение числа Прандтля для жидкости при определяющей температуре; v — коэффициент кинематической вязкости газа при определяющей температуре, м²/с; g = 9.81 м/с²— значение ускорения свободного падения; в — температурный коэффициент объемного расширения, 1/К.

Тепловой баланс пробирки (без учета теплообмена излучением):

Q- = Qnp + Qж,                (37)

где Q_конв — количество теплоты, затрачиваемое на нагрев системы "пробирка—жидкость" через конвективный теплообмен, Дж; Q_пр — количество теплоты, расходуемое на нагрев пробирки, Дж; Q_ж — количество теплоты, затрачиваемое на нагрев жидкости, Дж.

Количество теплоты, затрачиваемое на нагрев системы "пробирка—жидкость" через конвективный теплообмен:

Qkohb = Q • t.                       (38)

Количество теплоты, расходуемое на нагрев пробирки:

Q = c -m -NT ,            (39)

пр пр пр пр , где cпр — теплоемкость материала пробирки, Дж/(кгК); тпр — масса пробирки, кг; АТпр — разность между конечной и начальной температурой пробирки, К.

Количество теплоты, затрачиваемое на нагрев жидкости:

Q = c -m -M ,           (40)

жжж ж, где сж — теплоемкость жидкости, Дж/(кг!К); тж — масса жидкости, кг; АТж — разность между конечной и начальной температурой жидкости, К.

Дифференцируем приведенные выше зависимости по времени:

dQKOHB = dQnp + dQж .  dQKOHB dtdtdtdt

dQпр	dTпр	dQ	dTж
= с„• m„„	•----------------;	-----= с, • m„„
dt    спр mпр	dt	dt	dt

Для получения упрощенной записи дифференциального уравнения изменения температуры жидкости принимается допущение о равенстве скоростей изменения температуры жидкости и температуры пробирки dТж dtt = dТпр /dt, и дифференциальное уравнение изменения температуры жидкости принимает вид dT       Q

ж

+ пр пр ж ж

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ, ПРОИСХОДЯЩИХ В ПНЕВМАТИЧЕСКОЙ СИСТЕМЕ ТЕРМОСТАБИЛИЗАЦИИ

ловных дросселях:

w = 0 ;     G0 = G1 = G₂= G₃= 0.        (45)

Давление рабочего тела в полостях устройства равно давлению окружающей среды:

Уравнения модели

P1 = P2 = P3 = Pа •               ⁽⁴⁶⁾

Для исследования переходных процессов разработана математическая модель, основанная на использовании системы обыкновенных дифференциальных уравнений. Перед составлением математической модели процессов, протекающих в исследуемом объекте, вводится ряд допущений:

• •    рабочее тело — идеальный газ, подчиняющийся термодинамическому уравнению состояния;

• •    процесс истечения — адиабатический (без теплообмена);

• •    поток газа — установившийся;

• •    течение газа происходит без трения (отсутствуют диссипативные силы).

Система обыкновенных дифференциальных уравнений, описывающих переходные процессы, протекающие в системе:

Напряжение на электрическом нагревателе отсутствует:

U = 0.                     (47)

Граничные условия

Тепловое взаимодействие рабочего тела с электрическим нагревателем описывается граничными условиями третьего рода:

Q = a * S *( Ten - T2) •               (48)

Тепловое взаимодействие рабочего тела с пробиркой описывается граничными условиями третьего рода:

Q = a1 *S1 (T3 -Тпр 1 ) = a2 *S2 •(Тпр2 -T.).     (49)

dP1 = — (RTG0 - RTG); dt V1 ( a 0

dT1 dt

=t (V^ -^RT(Ga^-G1⁾];

dTen _P - aS (Ten - T2).

----=------------------; ----= a * dt          cспmспd dp2 = — frtg - rt2g. dt V, (   112

dQ²(k -1) dt⁽     )

dT²= — ^fV—-RT₂(G, -G) + dQ²(k-1)); d t p₂V₂( ²d t^{2 ( 1 2}) d t⁽)y

Конечные условия

Конечным условием расчета является достижение заданной температуры жидкости в пробирке:

T =T жк^.

Решение

Решение полученной системы представляет собой задачу Коши для однородных дифференциальных уравнений. Такая задача формулируется в следующем виде:

dT.=____Q____; dQ = Q dt cm + cm     dt пр пр ж ж dp3 dt

—I RT₂G₂- RT₃G₃

^V3 V

dT³= -T³-^fV dp³- RT₃ (G₂ - G₃) - dQ³(k -1)' dt p₃V₃ V ³dt^{3 ( 2 3}) dt⁽ J

Начальные условия

В начальный момент времени температура спирали и температуры газа в объемах равны температуре окружающей среды:

T = T = T = T_c„ = T = Т_ж = T .       (44)

12   3 сп пр ж а

Скорость рабочего тела равна 0 и соответственно отсутствуют расходы рабочего тела в ус- dy

— = f (y, t),   t G[ t0, tn ],    y(t0) = y 0, dt

y(t) e Rm, f (y, t) e Rm.

В некоторых системах однородных дифференциальных уравнений (ОДУ), являющихся математическими моделями физических систем, возникает так называемое явление жесткости. Оно возникает в случае, когда в физических системах, описываемых этой системой ОДУ, протекают процессы с существенно отличающимися постоянными времени. Система ОДУ, описывающих переходные процессы, протекающие в пневматической системе термостабилизации является жесткой, т. к. постоянные времени процессов изменения давления и температуры в газовых емкостях различаются на несколько порядков.

Для решения жестких систем ОДУ использу- ются специальные жестко-устойчивые методы (методы Гира). Введение понятия жесткой устойчивости метода позволило сконструировать группу методов, в которых величина шага интегрирования выбирается так, чтобы быстро затухающие и не оказывающие существенного влияния компоненты решения аппроксимировались устойчиво, тогда как для компонент с большими постоянными времени гарантировалась точность аппроксимации. Наиболее распространенным классом линейных многошаговых методов для жестких задач являются "формулы дифференцирования назад" (более общее название — методы Гира). Вычислительная формула методов Гира основывается на интерполяционной формуле Лагранжа для правой части системы ОДУ:

^{f (}tm+1,ym+1)      ,    ^i=0 aiym-i+1 ;

hm+1

ai = t m tm-1. П tm tm-p , i = 1,2,...,k;

t -t . Л^Л -t m     m - i p=1, p * i m - i     m - p a о =-X k==1 aj •

Табл. 1. Физические свойства сухого воздуха при давлении p_а= 1.013 -10⁵Па

t, °С	р, кг м3	X-102, Вт/ (мхК)	v-106, м2с	Pr
0	1.293	2.44	13.28	0.707
10	1.247	2.51	14.16	0.705
20	1.205	2.59	15.06	0.703
30	1.165	2.67	16.00	0.701
40	1.128	2.76	16.96	0.699
50	1.093	2.83	17.95	0.698
60	1.060	2.90	18.97	0.696
70	1.029	2.96	20.02	0.694
80	1.000	3.05	21.09	0.692
90	0.972	3.13	22.10	0.690
100	0.946	3.21	23.13	0.688
120	0.898	3.34	25.45	0.686
140	0.854	3.49	27.80	0.684
160	0.815	3.64	30.09	0.682

Выражение, приведенное выше, представляет собой нелинейное уравнение относительно ym+1. Для вычисления начального приближения ym^j по значениям y_m, y_m-1,...,y_m-_k строится интерполяционный полином k-го порядка для функции y(t) и посредством экстраполирования вычисляется значение ym^. Следует заметить, что по этим формулам можно вести интегрирование с переменным шагом. Вместе с тем при фиксированном шаге коэффициенты a_i не изменяются, что существенно упрощает метод.

РЕЗУЛЬТАТЫ РАСЧЕТНО-ТЕОРЕТИЧЕСКИХ ИССЛЕДОВАНИЙ

В пневматической системе термостабилизации в качестве рабочего тела используется сухой воздух со следующими характеристиками: R = 287 Дж/(кгхК), к = 1.41. В табл. 1 приведены физические свойства сухого воздуха, используемые в расчете, в зависимости от температуры.

Параметры окружающей среды принимаются равными нормальным условиям (температура окружающей среды Т_а = 300 К, давление окружающей среды p_а= 1.013 -105 Па ).

Термодинамическая расчетная схема пневматической системы термостабилизации (рис. 1) представлена в виде набора трех газовых емкостей, разделенных между собой, (объем первой емкости V= 5 -10^-5м³, объем второй емкости

V₂= 3.5 -10 6 м³, объем третьей емкости V3 = = 9 -10^-6м³).

Газовые емкости отделены от подводящих и отводящих магистралей условными дросселями (площадь условного дросселя, соединяющего первую и вторую газовые емкости, f₁₂ = 2 -10^-4м²; площадь условного дросселя, соединяющего вторую и третью газовые емкости, f ,₃= 2 -10^-4м²; площадь условного дросселя, соединяющего третью газовую емкость с окружающей средой, f „ = 6.5 -10^-4м²).

В качестве побудителя расхода используется вентилятор с максимальным расходом, равным G₀= 0.25 -10^-3м³/с.

В качестве электрического нагревателя используется проволока из нихрома (диаметр проволоки: d = 0.3 -10^-3м, общая длина проволоки: L = 0.5 м, теплоемкость нихрома: снихром = 448 Дж/(кг^хК), плотность нихрома: рнихром = 8800 кг/м³). Мощность, подводимая к электрическому нагревателю, составляет P = 8 Вт.

Пробирка изготовлена из полипропилена. Коэффициент теплопроводности полипропилена Хпр = 0.2 Дж/(мхК). Теплоемкость полипропилена спр = 1927 Дж/(кгхК). Внутренний диаметр пробирки d₂= 3 -10^-3м. Внешний диаметр пробирки d 1 = 3.5 -10^-3м. Длина пробирки l = 1 -10^-2м .

Табл. 2. Физические свойства воды на линии насыщения

t, °С	X • ю2, Вт/ (мхК)	v •Ю6, м2с	Pr	в •Ю4, 1K
0	55.1	1.789	13.67	–0.63
10	57.4	1.306	9.52	+0.70
20	59.9	1.006	7.02	1.82
30	61.8	0.805	5.42	3.21
40	63.5	0.659	4.31	3.87
50	64.8	0.556	3.54	4.49
60	65.9	0.478	2.98	5.11
70	66.8	0.415	2.55	5.70
80	67.4	0.365	2.21	6.32
90	68.0	0.326	1.95	6.95
100	68.3	0.295	1.75	7.52

Рис. 6. Зависимость температуры элементов расчетной схемы (рис. 1) от времени.

Tсп — температура спирали; T1 — температура газа в первом объеме; T2 — температура газа во втором объеме; T3 — температура газа в третьем объеме; Tж — температура жидкости в пробирке

Масса пробирки m = 3 -10"⁵кг . В пробирке находится жидкий биологический препарат, физические параметры которого сходны с физическими параметрами воды. Теплоемкость воды c = 4200 Дж/(кгхК). Масса воды m = 5 • 10^-5кг . В табл. 2 приведены физические свойства воды на линии насыщения, используемые в расчете, в зависимости от температуры.

Рис. 7. Зависимость избыточного давления газа в объемах от времени (расчет).

p₁— избыточное давление газа в первом объеме; p₂— избыточное давление газа во втором объеме; p3 — избыточное давление газа в третьем объеме

Рис. 8. Зависимость температуры элементов 3-й емкости от времени (расчет).

T3 — температура газа в третьем объеме, Tж — температура жидкости в пробирке; Tст1 — температура наружной стенки пробирки; Tст2 — температура внутренней стенки пробирки

На основе предложенной математической модели проведены расчетно-теоретические исследования переходных процессов, происходящих в пневматической системе термостабилизации. Результаты представлены на рис. 6, 7, 8.

Рис. 9. Конструктивная схема экспериментального стенда

ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТЕОРЕТИЧЕСКИХ ДАННЫХ, ПОЛУЧЕННЫХ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Нагреватель установки (рис. 1, 9), обеспечивающий нагрев рабочего тела, и вентилятор, обеспечивающий прокачку рабочего тела, потребляют энергию от внешних источников питания.

Регулирование температуры внутри рабочей камеры происходит двояко:

• •    изменением напряжения на нагревателе, что приводит к изменению его температуры, а следовательно, и температуры рабочего тела;

• •    управлением расхода вентилятора путем изменения напряжения, подаваемого на вентилятор, а следовательно, и скорости вращения вентилятора.

Все изменения температуры фиксируются термодатчиками, расположенными в рабочей зоне и в пробирке, и передаются для обработки и визуализации на ЭВМ (рис. 9). Сигнал с термодатчика поступает в устройство сопряжения, представляющее собой аналого-цифровой преобразователь, где он из аналогового сигнала преобразуется в цифровой. Цифровой сигнал кодируется и по последовательному интерфейсу передается в персональный компьютер, который декодирует полученную информацию и выводит ее на монитор в виде графика изменения температуры.

Датчик 1 и датчик 3 фиксируют температуру газа в третьем объеме. Датчик 2 фиксирует температуру жидкости в пробирке. В эксперименте использовались датчики фирмы HONEYWELL Hel 700-Txx со следующими характеристиками:

• •    Диапазон рабочих температур:   -200^+540 °С;

• •    сопротивление при 25 °С:       100 Ом;

• •    время ответа:                    0.01 с;

  

  Рис. 10. Зависимость температуры от времени (эксперимент).

  Т1 — температура газа в первом объеме; Т2 — температура газа во втором объеме; Т3 — температура газа в третьем объеме; T_сп — температура спирали;

  Т_ж — температура жидкости в пробирке; Т3(э) — температура газа, измеренная датчиком 1;

  Тж(э) — температура жидкости в пробирке, измеренная датчиком 2

  
  

• •    точность температуры:

• •    рекомендуемый измерительный ток:

• •    чувствительность:

  ±0.2 °С;

  1 мА;

  0.3 Ом/град.

  
  

Экспериментальные результаты представлены на рис. 10.

Фирма Roch [15] в качестве емкостей для жидкости использовала вместо стандартных полипропиленовых пробирок тонкостенные капилляры

Рис. 11. Динамика температуры жидкости в тонкостенном капилляре в зависимости от температуры наружного воздуха. Данные фирмы Roch диаметром 1.5 мм и максимальным объемом 20 мкл. Капилляры имеют большее отношение площади поверхности капилляра к объему капилляра по сравнению с полипропиленовыми пробирками, что позволяет достигать больших скоростей нагрева и охлаждения. Об этом свидетельствуют данные, приводимые фирмой (рис. 11).

ВЫВОДЫ

Как видно из рис. 6, температура в 1-й газовой емкости практически не изменяется и равна 20 °С, т. е. равна температуре окружающей среды. Температуры во второй и третьей газовых емкостях практически равны между собой в каждый момент времени.

Как видно из рис. 7, максимальное избыточное давление соответствует первой емкости и составляет чуть более 3 Па. Следовательно, можно пренебречь распределением давления по газовым емкостям и считать его постоянным и равным давлению окружающей среды:

p1 = p2 = p3 = p_а= 1.013 -105 Па = const.

Скорость нагрева жидкости в полипропиленовой пробирке меньше скорости нагрева воздуха, которым омывается пробирка. Этого не наблюдается при использовании тонкостенного капилляра с большим отношением площади поверхности капилляра к объему капилляра. Там температура жидкости практически не отстает от температуры газа (рис. 11). Для достижения больших скоростей нагрева и охлаждения необходимо использовать тонкостенные капилляры.

Предложенная математическая модель позволила оценить масштабы переходных процессов, протекающих в пневматической системе термостабилизации в режиме нагрева. Средняя скорость повышения температуры жидкости меньше средней скорости повышения температуры воздуха, которым омываемся пробирка с жидкостью.

Для более полного исследования процессов, протекающих в пневматическом амплификаторе, необходимо прибегнуть к математической модели, учитывающей распределенные параметры.

Работа выполняется при частичной поддержке госконтракта № 02.467.11.3005. с Федеральным агентством по науке и инновациям.