Разработка математической модели распределения сил натяжения по ширине полосы при горячей прокатке в непрерывной группе стана 2800

Как известно, в процессе прокатки листа его толщина непрерывно изменяется как в направлении длины проката – продольная разнотол-щинность, так и в направлении его ширины -поперечная разнотолщинность. Существуют эффективные системы регулирования толщины по длине полосы, и их теория хорошо разработана [1]. Иное положение с поперечной разно-толщиностью и связанного с ней показателя, называемого планшетностью.

Планшетность характеризует соответствие изделия плоской форме. Если поверхности, ограничивающие полосу с прямоугольным сечением по толщине, являются плоскими, то говорят что она планшетная [2] (рис. 1 а). Если же полосу невозможно ограничить по толщине прямоугольными поверхностями, то говорят о её не-планшетности (рис. 1 б).

Непланшетность вызвана неравномерным распределением обжатий по ширине полосы, что приводит к несоответствию профиля полосы до и после деформации. Более деформируемые участки полосы испытывают большую деформацию в продольном направлении, и “тянут” за собой менее обжатые участки, которые естественно “сопротивляются” этому воздействию, т.е тормозят развитие деформации в продольном направле-

нии. В результате в менее обжатых участках возникают растягивающие напряжения, а в соседних сжимающие, что приводит к короблению листа или непланшетности (рис. 2).

Особая сложность по определению и устранению непланшетности возникает при горячей прокатке в непрерывных многоклетьевых станах (рис. 3).

В таких станах полоса выглядит плоской даже тогда, когда неравномерность деформации по ширине листа уже достигла уровня потери устойчивости. Говорят, что в этом случае имеет место скрытая непланшетность, которая геометрически будет проявляться во время холодной прокатки. О наличии скрытой непланшетности при прокатке в непрерывной группе стана можно судить только по неравномерности распреде-

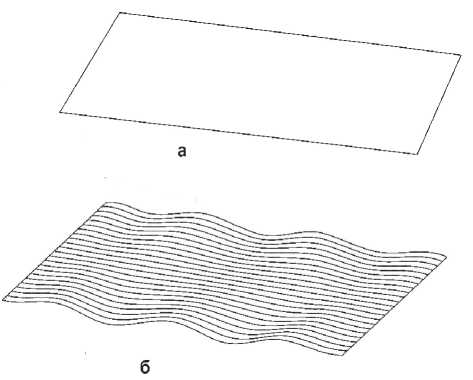
Рис. 1. Форма полосы:

а – полоса планшетная; б – полоса, на которой наблюдается непланшетность

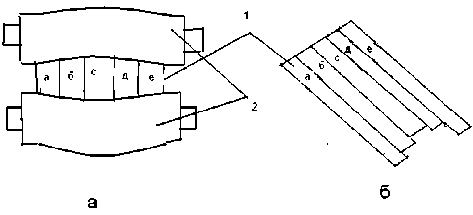
Рис. 2. Механизм образования непланшетности: а – полоса в очаге деформации; б – схема развития деформации;

1 – валки; 2 - полоса

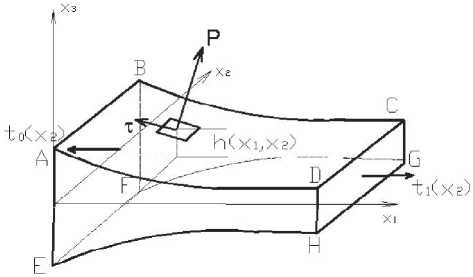
Рис. 4. Схема очага деформации при прокатке в непрерывной группе

ления продольных сил натяжения по ширине полосы. Другими словами, данные о распределении величины удельного натяжения по ширине полосы равносильны информации о планшетности.

В связи с этим разработка математической модели определения продольных сил натяжения по ширине полосы при горячей прокатке в непрерывной группе стана 2800 весьма актуальна.

Рассмотрим деформацию прокатываемой полосы в непрерывной пяти-клетьевой группе стана 2800 (рис. 4). Известными величинами здесь являются: геометрические параметры профиля проката на входе в стан; размеры рабочих валков; обжатие получаемое металлом в каждой клети, а так же предел текучести материала и мощность привода стана. Необходимо определить распределение продольных сил натяжения, изменение геометрических размеров валка и величину давления на металл на выходе из каждой клети.

Профиль валка зададим следующей функцией

5 h ( x 1 , x ₂ ) — величина упругой деформации валков;

H₀ i , H 1 i - заданные входная и выходная номинальные толщины.

Введем допущение, что скорость полосы по x ₃ можно задать линейно изменяющейся и равной v₃=0 на плоскости симметрии x 1 Ox ₂ . Находим, её по следующему выражению

v 3

( дh     дh ) x3

—v 1 + v 2 — vdx 1      дx 2 J h ’

где v1, v2, v3 – скорость полосы на осях 1,2 и 3

соответственно

Таким образом, задача сводится к определению проекций скорости полосы на плоскость

x _l Ox ₂

^f v i ⁽ x x 2)' ,v , ( x i , x , ),

Для того, чтобы найти их, разо-

x ₃ = h ( x 1 , x ₂) =

(x L д )

R

+ H _u + 8г ( x i , x 2 ) , (1)

где R – радиус рабочего валка;

Lд– длина недеформированной дуги контакта

L Д =V( H « i - H J* R ;

Рис. 3. Пятиклетьевая непрерывная группа прокатного стана “Кварто 2800”

бьем плоскость x 1 Ox ₂ на прямоугольные девятиузловые конечные элементы [3] (рис. 5).При этом скорости v 1 ( x 1 , x ₂ ) и v ₂ ( x 1 , x ₂ ) будут определяться во всех девяти узлах конечного элемента а давление у₀ (х₁,х₂) только в четырех узлах (1, 2, 3, 4) (рис. 6.)

Как следует из метода конечных элементов [4] непрерывная функция в узлах области решения аппроксимируется по следующей формуле.

V = [ N i , N j , N k ....^ [ ^ ] . (3)

где ^ - значения искомой величиныв узлах элемента;

N – функция формы элемента с соответствующим номером узла в = i, j. к и.т.д.

В нашем случае функции формы элемента в локальных координатах для девяти узлов записываются следующим образом

N 1 = 4( 5 ² - 5 )( п ² - п ) ,

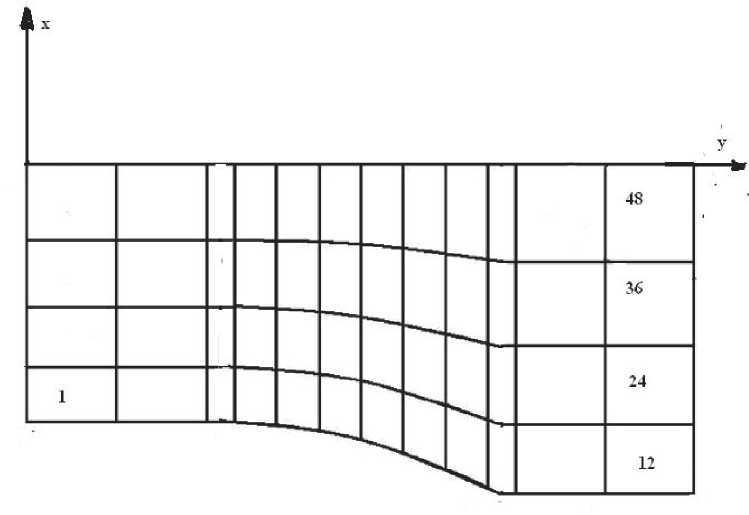
Рис. 5. Разбиение области решения на конечные элементы

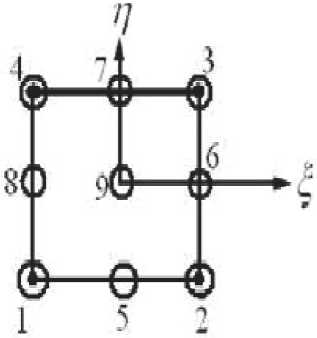
О Узлы в которых находиться только скорость

0 Узлы в которых находится скорость и давление

Рис. 6. Девятиузловой конечный элемент

( П , 5 — локальные оси координат в конечном элементе)

N з = 1( 5 2 + 5Хп ² + п ) , N 4 = 1( 5 ² - 5 ) П 2 + П ) , N 5 = |<1 - 5 ²Хп² + п ) , N 6 = 4( 5 ² + 5 X1 - п ’), N 7 = 4(1 - 5 П² + п ) , N 8 = 1(5² - 5 X1 - п ² ) , N 9 = 1 ^{( 1} - 5 ² I¹ - п ² ) .

Зададим уравнения для определения неизвестных функций. Это будут два уравнения равновесия по осям x ₁ и x ₂ и условие неразрывности. При этом исходим из допущения что проекцией давления металла на валок на ось x ₂ можно пренебречь:

Q x ₁

+ д(^12 h) - p дh +     АЧ

^ x 2        ^{d x} 1    -J A v₁ 2 + v ₂ 2

т = 0 ;(5)

d ( ^ ]h ) d ( ^₂ h ) v₂ ^X T⁺

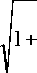
т = ⁰ ;(6)

V^{d x} 1 J

(5 h )

5 x ₁        5 x ₂

где <7₁₁ , CT ₂₂, CT ₁₂ — компоненты тензора напря-(4) жений, ct ₁₃ = ст ₂₃ = 0 ;

p - величина нормального давления металла на валок.

A v 1 = V - v i , V В ^- линейная скорость валка.

T - напряжение трения касательное к поверхности валка.

Принимаем следующий закон трения: т = mos, где m - показатель трения, os - предел текучести материала.

Граничные условия для уравнений (3), (4), (5) ст_п = t i ( x 2 );                   (8)

t 1 ( x 2 ) — равномерное натяжение (известное из начальных условий) на поверхностях ABFE и DCGH,

Для того чтобы воспользоваться уравнениями (5, 6, 7) в методе конечных элементов, необходимо привести их к уравнениям следующего вида:

j N^L ( ф ) dR = 0 , р = i, j, к....,      (9)

R где R – область интегрирования;

L( у ) - дифференциальное уравнение, определяющие у .

Затем мы аппроксимируем функцию ^ в узлах конечного элемента с помощью формулы (3), где ^ - узловые значения искомой величины.

Для того чтобы привести уравнения (5, 6, 7) к дискретному виду, воспользуемся методом взвешенных невязок с весовыми функциями w_p ( x 1 , x ₂ ) - для уравнения неразрывности и W 1 ( x 1 , x ₂ ) , w ₂ ( x 1 , x ₂ ) - для уравнений равновесия. Через A обозначена область интегрирования, представляющая собой пересечение плоскостью x ₁ Ox ₂ .очага деформации (фигура ABCDEFGH на рис. 2). Тогда интеграл взвешенных невязок запишется следующим образом

ных выше преобразований выражение (10) запишется следующим образом:

¹ = ¹ 1 ^{+ 1} 2 ^{+ 1} 3 ^{+ 1} 4 ^{+ 1} 5 ,

где I, = I ^{v 11} —- + ——— I w„dx,dx₂

¹        ( d x 1          d x ₂ ) ^{p 1 2}

I 2

-If h

A

I 3

I 4

V

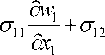
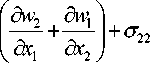
a w i ' d x _{2 V}

w 1 dx 1 dx ;

c ° 11 h ) + < ^hv )

d o h ) d o h )    c h A v   )

₊ 1'' — p — ₊ i т wdxdx + G x   e x   e x ^Ati^ )

f| ( ⁰ ) A ^{0 h} -   ^V 2

A ( G x     G x   ^ Av + V ₂ 2

(d h )

1+1 , I ^T Wdxdx

(e x ) V

В выражении (7) применяем интегрирование по частям. Для второго и третьего интегралов применяем формулу Грина [4] чтобы исключить производные по компонентам тензора напряжений. Для удобства записи выражение (10) представим как сумму I = I 1 + 1 ₂ + 1 3 + 1 4 . С помощью ввода в выражение (10) интеграла I₅ учтем граничное условие о 1 1 = t 1 ( x ₂ ); . Через г обозначена область интегрирования, представляющая собой пересечение прямоугольника DCGH (плоскости выхода металла из очага деформации, на котором мы задаем базовое значение натяжения) c плоскостью x ₁ Ox ₂ . С учетом описан-

d h A v

P--- /       ¹ т

2~

A (  ^d x ¹    д/^А V 1 ⁺ V 2    )

w ₁ dx ₁ dx ; (11)

-Л

A

v ₂

V A V 12 + V 2 2

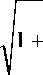
[f ^h

V^d x 1

t w ₂ dx 1 dx

2 ^;

1 5 = if ht 1 ( x ₂ ) w 1 d Г г

Предполагаем, что материал жестко пластический. Cледовательно, зависимость напряжений от деформаций можно выразить так:

0- 11 = a ₀ +п£и ; a ₂₂ = a ₀ +ns 22 ; cr₁₂ = nf 12 ; (12)

СУ eq n = —— Oeq - интенсивность девиатора напряжений, 3 £ eq

_{£ eq} - интенсивность тензора скоростей де .

формации. Зависимость y _eq от £ _eq может быть получена по результам лабораторных испытаний на осадку или кручение.

Компоненты тензора скоростей деформации выражаются через скорости

■       d v,      ■       d v₂      ■ ■       1 (d v, d v ₂)

£ 11 = —1; е 22 = —; £ 12 = е 21 =-I — ¹ +—I;

e x j          O x ₂               2 (e x ₂    e x j )

Компонента тензора деформации

( d h

d h ^

⁰ 33 = ⁰ 0 ⁺ П —v 1 ⁺ —v 2

V d x 1       d x ₂    )

.

Используя (12, 13 и 14) и предполагая p = — 0 33 интегралы 1 2 и 1 ₃ из выражения (11) можно переписать так:

¹ 2 =

( 3 3              ^

ff ^{h o} 0 ^{( £} 11 ⁽ w ^{)+ £} 22 ⁽ w " +■ dx 1 ^dx 2 ⁺ jj ^{2r h} УУ й , ⁽ w k^{( v )} w f ^dx 1 ^dx 2

A                                   A    V i = 1 j = 1             V

Я (д h 1 ) , ,       1 (d h d h ) , ,

— - ^y 0 w ] dx ! ^dx 2 ⁺ | XT)- —^V 1 ⁺ — ^v 2 w 1 ^dx 1 ^dx 2 e x, h h hk a x,      a x₇

A 1                       A 1         2

Тогда сумма интегралов I выражается через неизвестные функции v 1 ( x 1 , x 2 ) , v 2 ( x 1 , x 2 ) и — 0 ( x 1 , x 2 ) и соответствующие им весовые функции w_p , w ₁ , w ₂ .

Теперь уравнения вида (11) приведенные к виду (9) аппроксимируем в соответствии с уравнением (3):

f

V T d h \ '

^[ K vv ^] - JJ - 2 n h ^{([ B ] T [ B} ] ) +^{( [} N v ■ m 2)) /^ h-

\ d x₂

V ' 2

v ₁ e ₁

[ N v ] dx 1 dx 2

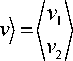
- [ N ] v‘ -

^— o

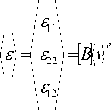
N e x

2 ay E 2

N 1 0 N ₂ ... 0 N 9 0

. 0 N 0 N 2 .. N 8 0 N 9 _

e ^v 21

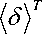
V

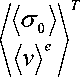
^{7 —} 01 ,... ^— 0 np , ^v 1 ,...., ^v 2 nv^

; (24)

...

;

^v 91

^v 9 ^e 2

- ( N ") - 0) = ( n 1 p , N p , N 3 ,

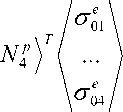
0	N		a y.	0	1 ve 1
	e x		e x		e
а\ ]	0	a\ 8	0	a y,	/ v 2i
e x	..	e x		9(2	E.'
2 a\f	2 a\2	2 a \,	2 a y,	2 a y,	e
22 e x	22 9(2	22 9(1	22 9(2	22 9 ] _	\v^

(18.а)

Для вычисления интеграла I5 по поверхности Г аппроксимируем натяжение на поверхности DCGH следующим выражением:

t1e t (x2 ) = (N], N2, NBf t2 .    (19)

t 3 ^e

Теперь, когда функции представлены дискретными величинами согласно методу конечных элементов [4], построим матрицу жесткости.

[0] [K« ]1[[K„ ] [Kv ]J

где

^[ K - v ^] ' = JJ ( ^N')

A

'

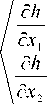
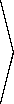
Tri.

[ N ] + hm [ B ] dx , dx 2 ; (21)

[ K - ]— JJ | h ( [ Bm ) \   -[| h 1 И N^v ] ^Tm ₂)) N P ) I . dx 2 ;

A V                 V^ x h )               )

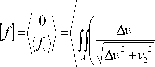
[ N ] ^Tlm2) +     v ² 2 [ N ]T( m ,)j dx i ^dx2 + J hN BT t 1 ) d ^r

■^ A v ] + v 2             ) Г /

Граничные условия (8) учтены интегралом по контуру Г , с использованием криволинейных аппроксимирующих, функций составляю-

щих вектор N B .

Чтобы составленная с помощью матрицы жесткости система уравнений имела решение введем еще одно допущение. Предполагаем, что на поверхности DCGH действуют только напряжения у11 = t(x2) и у33.

В таком случае тензор напряжений примет вид

[-]-

t ( x ₂ )

^{0   -} 33

Тогда условие пластичности и формулу для определения нормального всестороннего сжатия у0 для указанных поверхностей можно записать как

t ( x ₂ ) 2 - 1 ( x ₂ ) — ₃₃ + — ₃ ² ₃ - — _т ² / 3 ; (27)

^- 0 ^- 3^{( -} 1 ^{+ -} з ) ,          (28)

здесь — _т предел текучести. Разрешая (27) относительно — ₃₃ и подставляя полученное значение в выражение (28) получаем

- 0 (x 2)-

Модифицируем систему уравнений (21) следующим образом: удаляем все уравнения соответствующие узлам — 0, лежащим на границе DCGH, Столбцы матрицы [Kv— ], соответствующие этим узлам, умножаем на значения полученные по (29) и переносим в правую часть, модифицируя вектор f . Таким образом, мы определяем силовые условия в узлах, примыкающих к DCGH и система уравнений становится разрешимой.

В результате решения системы уравнений (21) получаем вектор гидростатических давлений и скоростей течения металла (20). При моделировании прокатки в непрерывной группе клетей количество элементов для всех клетей выбираем одинаковым. Эти скорости зависят от распределения межклетьевых натяжений по ширине задаваемых граничным условием (8). Введем в рассмотрение функцию, представляющую собой рассогласование указанных скоростей

^Ф ij ^ t 1 ,---, t N ^ = v j - vi + 1 j ,      (30)

где N – количество клетей непрерывного стана;

Vj - выходная скорость в узле j клети i стана; о vi+1 j - входная скорость в узле j клети i + j t – вектор узловых значений переднего натяжения для клети i

Искомым распределением натяжений будет такое при котором

Ф j^ t — ,..., t N , V j ... V n ) = 0 . (31)

Кроме того, интегралы удельного натяжения по поверхности DCGH должны быть равны полному межклетьевому натяжению T i , заданному как исходное данное в условиях задачи, в соответствии с (21)

NeB T

ZJ ^Ns (t)dx 2 = T i .       (32)

¹ г

Число неизвестных в уравнениях (31),(32) равно количеству узлов в которых заданы натяжения, во всех клетях плюс количество клетей. Распределение натяжений, которое обеспечивает выполнение все этих равенств является решением при форме межвалкового зазора заданного выражением (1). Система уравнений (31) (32) нелинейная. Для ее решения применим последовательные приближения. В качестве начального приближения можно принять равномерное распределение натяжения. Допустим, что на очередном шаге вычислений распределение натяжений по клетям задано последователь-

/ - 0       - 0 \ ностью векторов (t 1,....,tN )и скоростей

VV1°..V_N У Тогда следующее приближение найдем из линеаризованной формы (31), (32):

УФ V - Vk )+Z к д Vk kl

^Ф - ( t„

6 t kl

-

t

0 kl

+ Ф ij

(-     -A

10     10  7/07/0

t 1 ,..., tN ’ V 1.. V N vУ

= 0 ;

NeB T

ZJ(N«) (t)-(t0>2 = 0, q г где k – номер приближения q – номер сечения в котором находится значение натяжения.

Частные производные вычисляем как конечные разности, для этого решаем систему (18) при малых изменениях только одного из узловых значений натяжений. Расчет заканчиваем по достижению сходимости по модулю векто-

0 ра разности \t] - ( t ).

После каждого решения (18) производим пересчет упругих деформаций валков 5 h ( x 1 , x ₂), пользуясь известными методиками и аналитическими решениями для упругих деформаций полубесконечного тела под действием поверхностных нагрузок [5]. Таким образом, с помощью полученной математической модели можно определить распределение значений натяжений и давлений метала на валок по ширине прокатываемой полосы. Алгоритм реализации математической модели представлен на рис. 7.

ВЫВОДЫ

• 1.    Образование непланшетности и разнотол-щинности листов и лент при горячей прокатке является следствием разной степени обжатия по ширине прокатываемой полосы, возникающей из-за упругой деформации валков.

• 2.    Разработана конечно-элементная модель прокатки алюминиевой полосы в пятиклетьевом непрерывном стане горячей прокатки, позволяющая на основе заданных технологических параметров определить требуемую величину меж-клетьевого натяжения прогиб и упругую деформацию валков обеспечивающие равномерные обжатия по ширине полосы.

• 3.    Предложен алгоритм компьютерной реализации математической модели.