Разработка математической модели системы оценивания полисостава газовых сред и алгоритма оценивания ее параметров по данным натурного эксперимента

Контроль наличия и количества различных примесей в атмосфере является весьма актуальной задачей, например, при экологическом мониторинге, при обнаружении утечек бытового газа или при управлении технологическими процессами на химических производствах. При выборе методов и средств оценивания состава газовых сред (концентрации компонентов сред) обращается внимание на достижение достаточной чувствительности, стабильности и в итоге — точности, что в значительной степени зависит от принятой модели средства оценивания состава газовых сред. Эта задача существенно усложняется при оценивании полисостава среды, то есть при одновременном оценивании концентрации ряда компонент, составляющих среду или присутствующих в атмосфере.

В известных работах [1, 2, 3] и др. для решения указанной задачи предлагается использовать сенсорные матрицы и сенсоры с температурным программированием. Во всех указанных работах предполагается использовать по одному каналу (датчику, сенсору, фильтру) для оценивания каждой компоненты. При этом характеристики каналов так или иначе линеаризируют. Такой подход — достаточно грубое приближение к решению поставленной задачи.

В действительности же каждый канал испытывает воздействие в той или иной степени всех компонентов газовой среды. Поэтому возникает задача разработки нового, более обобщенного метода оценивания компонентов на основе универсальной математической модели многоканальной системы, каждый канал которой имеет большую чувствительность к одной компоненте и менее чувствителен к другим, но влияние которых должно быть учтено на основе натурных экспериментов (градуирования системы). Это позволит повысить точность оценивания каждой компоненты и одновременно — получить интегральную оценку состава всей газовой среды.

Таким образом, основу предлагаемого метода составляют процедуры градуирования системы и ее математическая модель. Суть градуирования будет ясна в процессе синтеза математической модели. Поэтому уделим особое внимание модели.

Под математической моделью целесообразно понимать функцию преобразования всей системы (не отдельного канала), содержащую при этом линейную и нелинейную части типа:

y = y o + k • x + c • x⁹ .

Степень нелинейности варьируется в широком диапазоне. В общем случае для практических приложений показатель нелинейности g >  0 , g = 1 .

ТРУДЫ МФТИ. — 2011. — Том 3, № 3 Аэрокосмические исследования, прикладная механика 89

Будем полагать, что суммарный состав газовой среды содержит n различных составляющих, каждая из которых различным образом воздействует на канал (датчик, фильтр, сенсор) системы (рис. 1).

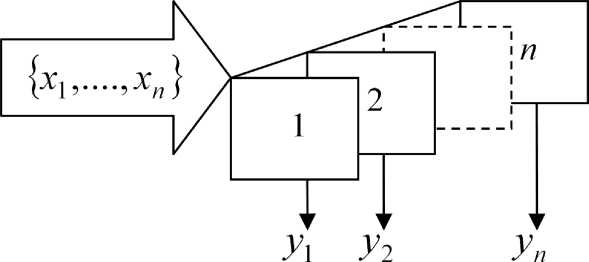
Рис. 1. Схема системы определения состава газовой среды

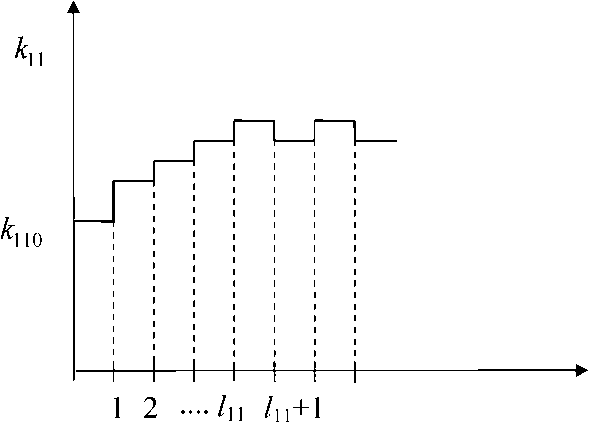
Рис. 2. Графики процесса итераций параметра k ₁₁ . Индекс l ₁₁ обозначает момент начала колебания значения параметра относительно определенного уровня

Пусть имеем { x 1 ,...,x n } — суммарный состав (полисостав) газовой среды, воздействующей на вход системы; y 1 — выходной сигнал с первого канала, y 2 — выходной сигнал со второго канала, y _n — выходной сигнал с n -го канала.

В связи с тем, что исследуемая среда воздействует на все каналы, то их функции преобразования можно записать вначале в упрощенном виде как систему линейных уравнений:

n

У з = У 0 + ^Lk ji X i j ^е { 1,2,...,n } ,

i =1

где x i — неизвестные величины — элементы (составляющие) полисостава, которые следует измерить (определить);

y 1 ,...,y _n — выходные сигналы каналов;

y ₁ ⁰ ,...,y _n ⁰ — начальные выходные сигналы каналов;

k 11 ,k 12 ,...,k 1 _n — чувствительности первого канала к x 1 ,...,x _n ;

k n 1 ,k n 2 ,...,k nj, ...,k nn — чувствительность n -го канала к x 1 ,...,x n ;

y 0 ,k ji — определяются в процессе индивидуальных градуировок всех (j ) каналов по каждой x i составляющей полисостава, j Е { 1,2,...,n } .

Последнее пояснение раскрывает особенности градуирования системы.

Решение поставленной задачи в виде решения системы (1) — весьма тривиально: оно не учитывает нелинейные составляющие выходных сигналов. Поэтому систему (1) приведем к нелинейному виду.

Для этого функцию преобразования каждого j -го канала представим по компоненте x 1 так:

У 11 = У 01 + k ii x i + C 11 x g ¹¹ ; ... ^;

, У п 1 = y n i + k n 1 x i + C n i x ^{g n1}

где y ₁ ⁰ ₁ ,...,y _n ⁰ ₁ — начальные выходные сигналы каждого канала;

y ii ,...,y _n1 — выходные сигналы 1,...,n каналов, обусловленные x 1 -й составляющей;

c 11 — коэффициент при нелинейной составляющей первого канала, выраженной степенной функцией x ^g ₁ ¹¹ ;

g 11 — показатель степени, соответствующий первому каналу для первой составляющей x 1 ;

c _n1 ,g _n1 — аналогичные коэффициент и показатель для n -го канала при x = x 1 .

Аналогичные функции преобразования можно записать для всех xi составляющих. Так, для xn получим yin = y0n + kinXn + cinxn1 n;

...;

y _nn = y _nn + k _nn x _n + c _nn x _n ⁿⁿ .

Для промежуточных систем вида (3) для x i , i Е { 1,...,n } будет использоваться символика y 1 i ,...,y _ni .

Теперь, используя (2), (3), систему (1) запишем в уточненном виде так:

nn yi = у0 + У^ kiiXi + У2 с^У;

i =1          i =1

У п = у П + У2 k ni X i + 52 C ni X g ni , i =1           i =1

n

0 = 1 V 7,0 • yi n / у y i i ;

i =1

где

...;

y n =

1 n

В системе

n

V y 0 i .

i =1

(4) неизвестны следующие параметры: y ⁰ , которые определяются через неизвестные

y 0 i ,...,y ni , а также неизвестные k _{i i} ; c _ii ,

...

^,k ni ; c ni ; ^g 1 i ^, '" ^,g ni ^.

Для нахождения этих параметров необходимо выполнить натурный эксперимент — произве-

сти градуировку системы по каждой составляющей газовой среды по определенной методике. Рассмотрим особенности методики градуирования системы.

Она будет состоять из n этапов, каждый из которых определяется тем, что подаются на вход системы отдельно x1,x2,...,xn составляющие и снимаются соответственно со всех каналов сигналы yi; У2; •••; yn. Эти данные позволяют записать с учетом (3) частные функции преобразования для каждого канала по xi(xi Е {xii,xi2,...,xii,...,xim}):

y ii i = Уп + k ii x i i + c ii (x i i ) ^{g 11} ;

ynii — yn1 + knixii + cn1(x1i)gn1, где индекс i соответствует i-му значению x1 , заданному при градуировке (xi Е {xii,xi2,...,xii,...,xim}), m — соответствует числу точек, взятых по шкале xi.

При градуировке по другим компонентам x2,...,xn действия аналогичны. Так, при градуировке по xn(xn Е {xni,xn2,...,xni,...,xnm}) будем иметь аналогичные выражения частных функций преобразования в виде yini = y0n + kinxni + Cin(xni)g1n;

•••;

^y nni = ^y nn ⁺ k nn x ni ⁺ c nn ^(x ni

) ^{g nn} .

Теперь, имея значения { x ii ,x i2 ,...,x i i ,...,x i _m } ; ...; { x n i ,x _n 2 ,...,x ni ,...,x _nm } и соответствующие значения

{yiii,yii2 v,yiii,...,yiim}; ..4 {ynni,ynn2,...,ynni,...,ynnm}, можно определить параметры частных функций преобразования, если воспользоваться алгоритмом (аппаратом) решения систем условных уравнений, предложенным авторами.

Под алгоритмом в рассматриваемом случае будем понимать совокупность (последовательность) процедур, представленных лингвистически или аналитически: в виде математических выражений в соответствии с известными работами академика А.Н. Колмогорова, которая использовалась авторами в [4]. При разработке алгоритма воспользуемся математической моделью

ТРУДЫ МФТИ. — 2011. — Том 3, № 3 Аэрокосмические исследования, прикладная механика 91 системы, рассмотренной авторами выше, и используем при этом системы условных уравнений, предложенные авторами.

Систему условных уравнений для частной функции преобразования (для первого канала) по x 1 (первого уравнения системы (5)) представим в виде суперпозиции приближенного выражения функции преобразования и вариаций по всем параметрам:

y ii i = Уп 0 + k ilo x i i + C iio (x i i ) g ¹¹⁰ + a + ^y TT¹ в + ^d y ¹¹ Y + ^"i 5, V i,         (7)

¹¹⁰                               ∂y ₁⁰₁       ∂k 11       ∂c 11       ∂g 11

где производные имеют очевидные выражения:

∂y 11 i ∂y ₁ ⁰ ₁ ∂y 11 i ∂k 11 ∂y 11 i ∂c 11 ∂y 11 i ∂g 11

= 1;

— xi i ;

g 11

= x 1 i ;

— C 11 (ln X 1 i )X i 11 .

С учетом модели функции преобразования канала и конкретных значений параметров (y ⁰ i — y ⁰ i0 , k ii — k ilo , c ii — c iio , g ii — g iio ), введенных в (7), можем записать:

a + хив + x gi ¹⁰ Y + c ii (lnx i i )x i i ¹⁰ 5 — Ay ii i o , V i,                         (9)

Ay ii i o — y ii i - y iio - k iio x i i - c iio x i ¹¹⁰ ,                            (10)

где i E { 1,2,...,m } — индекс, задающий номер градуировочного значения на шкале градуировки. Крайний правый нижний индекс «0» означает начальное приближение.

Выражение (9) — линейная неоднородная система с неизвестными α,β,γ,δ . Ее решение — тривиальная задача, но пока для этого не найдены значения y ₁ ⁰ ₁₀ , k 110 , c 110 и g 110 .

Можно эвристически (приближенно) оценить g 110 : если графики градуировочных данных, допустим, вогнуты, то g iio > 1 , и его можно принять равным любому числу больше 1, например, 1,5 . Значения же y ₁ ⁰ ₁₀ , k 110 , c 110 оценим как решение следующей системы (линейной и неоднородной):

yoio + xiikiio + (xii)g110 ciio — yiii, где i E {1; m/2; m}. Это соответствует методу выбранных точек. Система (11) конкретно представится так:

y ^o io + x ii k iio + (x ii ) g ¹¹⁰ c iio — y iii ;

< y^o io ^{+ x} i m/ 2 k iio ^{+ ( x} i m/ 2 ^{) g} 1 ¹⁰ c iio ^— y ii m/ 2 ;                            ⁽¹²⁾

. y ^o io + X i m k iio + (x i m ) g ¹¹⁰ C iio — y ii m -

Далее необходимо найти оптимальные значения α,β,γ,δ , соответствующие всем данным натурного эксперимента (градуирования). Для решения этой задачи составим сумму квадратов:

m

S i — X P i (a + хив + X g ¹¹⁰ Y + C iio (ln хц)х ^д П ⁰ 5 - Ay ii i o ) ² ,                (13)

i =1

где Pi — вероятность появления данных (хц; yiii). Если данные равновероятны, то Pi — mi, и ее можно из рассмотрения исключить. Последнее соответствует равномерному заданию x1i . При неравномерном шаге

x 1 - x 0

Pi — ------ xm - x0

P m/ 2 —

x m/ 2 - x m/ 2 - 1 x _m - x 0

Неизвестные параметры α,β,γ,δ в сумме квадратов (13) должны быть выбраны так, чтобы S _i ^ min .

Необходимое условие min известно:

∂S 1

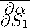
∂β ∂S 1 ∂γ ∂S 1 ∂δ

— 0;

— 0;

— 0;

— 0,

92 Аэрокосмические исследования, прикладная механика ТРУДЫ МФТИ. — 2011. — Том 3, № 3 которое представится в виде следующей системы:

' mm

X Pi[a + Хив + xfi10 Y + Ciio(ln xi^xfi10 5] = X Pi Ay°ii; i=ii mm

X P i [a + Хив + X i i ¹⁰ Y + c iio (lnx i i )x f i ¹⁰ 5] • x i i = X P i Ay iuoxu ;

i=1

m                                                   m(

X P i [a + Хив + Х ?Г ° Y + c iio (lnx i i )x i 1 ¹⁰ 5] • хЦ¹⁰ = X P i Ay ii i o x i ¹¹⁰ ;

i=i mm

X P i [a + Хив + x i i ¹⁰ Y + c iio (lnx i i )x f i ¹⁰ 5] • (Inx i i )x f _i ^{1 1} ° = X P i Ay ii i o (lnxjx f i ¹⁰ .

, i=i

Путь решения системы известен, например, по правилу Крамера или Гаусса. Пусть получим решение в виде значений а = a i , в = в 1 , Y = Y i , 5 = 5 i . Тогда уточненные значения (первое уточнение) параметров функции преобразования первого датчика найдутся таким образом:

' y ^o ii = y ^o io ^{+ a} i ; k iii = k iio + в 1 ; c iii = C iio + Y i ;

. g iii = g iio ^{+ 5} i .

Далее процесс итерации продолжается с учетом полученных уточнений (16). Для этого выражение (10) перепишем так:

Ayiiii = yiii - yiU - kiiixii - ciiixfi111, а (15) — в виде

X P i [a + X 1 i в + ■     Y + c iii (ln x i i )x ^g i ¹ i ¹¹ 5] = XX P i Ay ii i i ;

i=i mm y^ Pi[a + X1iв + xi111 Y + ciii(lnXii)xi11115] • xii = ^ PiAyiiiiXii;

• *   imi                                                        i=im

  X P i [a + X 1 i в + X i i ¹¹ Y + c iii (ln x i i )x ^{g 111} 5] • x f i ¹¹ = X P i Ay ii i i x f i ¹¹ ;

i=i

X P i [a + X 1 i в + x^ ¹¹ y + c iii (lnx i iK ¹¹¹ 5] • (lnx i^ ¹¹¹ = X P i Ay_U i i (lnx i )x ? 1 ¹¹ .

, i=i

Её решение составят числа a = a 2 , в = в 2 , Y = Y 2 , 5 = 5 2 .

С учётом этого вторично уточним значения параметров функции преобразования. При этом получим yii2 = yiii + a2; kii2 = kiii + в2;

c ii2 = c iii + Y 2 ; g ii2 = g iii + 5 2 .

Таким образом, определенная итерация продолжается до тех пор, пока не наступят колебания значений каждого параметра относительно определенных значений. Покажем это на графике, например, для кц (рис. 2).

Далее определим средние уточненные значения параметров функции преобразования первого канала: .П = ^N, (»)

где l — номер итерации.

ТРУДЫ МФТИ. — 2011. — Том 3, № 3 Аэрокосмические исследования, прикладная механика 93

Аналогично находятся k ii ,c ii ,g ii .

Далее изложенный процесс необходимо повторить для каждой оставшейся нерассмотренной компоненты X2,...,xn. После этого функция преобразования первого канала для совокупности всех компонент газовой среды может быть выражена с учетом частных функций преобразования по каждой компоненте в виде y1 = У11 + y12 + ... + yij + ... + yin =

= y ⁰ + (k 11 X 1 + k 12 X 2 + ... + kyX i + ... + k 1 n X n )+                      (20)

+ (C 11 X ^{9 1}1 + C 12 x 2 12 + ... + C 1 i X ^{9g 1j} + ... + С 1 п х П ^1п ),

• -0    ^y0 1 + ^y0 2 + ."+ ^{y 0}₃+ ."+ ^y0n •       9 X

где y ⁰ =----------- n-j--------, j € { l ^{, 2 ,} ... ^,n } .

Повторяя изложенные процедуры для всех каналов, получим совокупность их моделей — функций преобразования. Так, для канала с номером f выражение (20) по структуре останется таким же, но с измененной символикой, учитывающей конкретный канал:

y f = y f 1 _⁺ y f 2 ⁺ _." ⁺ y fj ⁺ ... + y fn =

= yf + (kf 1X1 + kf 2X2 + ... + kfiXi + ... + kfn Xn)+ + (Cf 1xgf1 + Cf 2x|f2 + ... + Cfixgfj + ... + CfnXnfn), где y0 =

y ⁰ i + y ⁰ 2 + ... + y ⁰ j + ... + y ⁰ n

n

.

Придавая произвольные значения f € { 1,2,...,n } , получим любую модель — функцию преобразования, соответствующую каналу с номером f .

Таким образом, нами изложена суть нового метода на основе разработанной математической модели многоканальной системы оценивания полисостава газовой среды, которая представляет собой систему взаимосвязанных функций преобразования отдельных каналов по всем компонентам газовой среды, включающих как линейные, так и нелинейные составляющие модели системы.

При этом функция преобразования каждого канала носит комплексный характер, так как учитывает воздействие на канал всей суперпозиции компонент газовой среды. Это выражает суть предложенного метода. Данный метод при разработке соответствующих алгоритмов обработки экспериментальных данных (данных градуирования — данных натурного эксперимента) позволяет повысить точность одновременного оценивания полисостава газовой среды.

Разработанный алгоритм оценивания параметров многоканальной системы оценивания полисостава газовой среды позволяет свести решение системы нелинейных уравнений к решению системы линейных неоднородных уравнений, что значительно облегчает решение поставленной задачи, а также учитывает все имеющиеся экспериментальные (натурные) данные градуирования и позволяет путем последовательных итераций определить указанные параметры с требуемой точностью. Перечисленные аспекты выражают достоинства разработанного алгоритма.