Разработка математической модели стадии нагрева резиновой смеси и синтез алгоритма управления нагревом с использованием принципа максимума Понтрягина

Приготовление и обработка резиновых смесей – важнейшая операция в шинном и резиновом производствах, от которой зависят пластоэластические и прочностные свойства, структура и гомогенность, а также технологичность смесей резиновых и резинокордных полуфабрикатов [1, 2]. На одном из участков в ЗАО «Воронежский шинный завод» используется резиносмеситель РС-270. Процесс приготовления резиновой смеси начинается с дозирования и загрузки сыпучих материалов из приемных бункеров в резиносмеситель. Заполнение производится системой шнековых питателей и весовых дозаторов. После происходит загрузка жидких ингредиентов, подогретых до необходимых температур. Часть операций производится в ручном режиме. Для отработки рецептов предусмотрен контроллер Siemens S-300 с дискретными и аналоговыми модулями расширения. Контроллер управляет дозированием компонентов, а также выгрузкой резиновой смеси по температуре и времени смешения.

Система управления нагревом резиновой смеси значительно устарела. С целью ее модернизации и повышения качества управления предлагается разработать математическое описание стадии нагрева и синтезировать алгоритм управления с использованием принципа максимума Понтрягина, который позволит снизить энергозатраты на нагрев резиновой смеси.

Результаты

Для стадии нагрева характерен интенсивный нагрев резиновой смеси в резиносмесителе до оптимальной температуры, путем подачи в него циркулирующего греющего теплоносителя (воды), который подается из теплообменного аппарата, а также за счет преобразования механической энергии (сил трения) в тепловую. Теплообменный аппарат обеспечивает нагрев теплоносителя путем подачи в него греющего пара высокой температуры. Греющий теплоноситель циркулирует в системе (вода после выхода из рези-носмесителя через циркуляционный насос попадает обратно в теплообменник), поэтому при составлении математической модели первой стадии также необходимо учитывать и теплообменный аппарат как орган управления. Так как теплообменный аппарат и резиносмеситель по своей структуре довольно схожи – продукт взаимодействует с теплоносителем через разделяющую стенку, то математическое описание для них будем выполнять по одной структуре.

Особенностью модели будет являться то, что выход теплообменного аппарата будет являться входом для смесителя и наоборот, а также будет необходимо учесть выделение тепла в результате перехода механической энергии смесителя в тепловую (при работе смесительных роторов).

Основная часть

Разработано математическое описание стадии нагрева [3–5], представляющее собой уравнения тепловых балансов для малого интервала времени ∆ τ и описывающее процессы нагрева теплоносителя в теплообменнике и дальнейшего нагрева им смеси в резиносмесителе:

для конденсата

Gp ⋅ I ⋅∆ τ = Gk ⋅ Tk ⋅ ck ⋅∆ τ +

+ Stp ⋅ α ts ⋅ ( Tk - Ts ) ⋅∆ τ + Mk ⋅ ck ⋅∆ Tk ;

для воды, нагреваемой в теплообменнике

Gv ⋅ Tvo ⋅ cv ⋅∆ τ + S ⋅ α ps ⋅ ( Ts - Tv ) ⋅∆ τ =

= Gv ⋅ Tv ⋅ cv ⋅ ∆ τ + Mv ⋅ cv ⋅ ∆ Tv ;

для стенки между конденсатом и водой в теплообменнике

S ⋅ α ts ⋅ ( Tk - Ts ) ⋅∆ τ =

= S ⋅ α ps ⋅ ( Ts - Tv ) ⋅∆ τ + Ms ⋅ cs ⋅∆ Ts ;

для воды, выходящей из резиносмесителя (после теплообмена)

Gv ⋅ Tv ⋅ cv ⋅∆ τ = Gv ⋅ Tvo ⋅ cv ⋅∆ τ + S 2 ⋅

⋅ α 2 ts ⋅ ( Tvo - T 2 s ) ⋅∆ τ + Mvo ⋅ cv ⋅ ∆ Tvo ;

для стенки между водой и резиновой смесью в резиносмесителе

S 2 ⋅ α 2 ts ⋅ ( Tv - T 2 s ) ⋅∆ τ = S 2 ⋅ α 2 ps ⋅

⋅ ( T 2 s - Tvo ) ⋅∆ τ + M 2 s ⋅ cs ⋅∆ T 2 s ;

для резиновой смеси, нагреваемой в рези-носмесителе

N ⋅ Kp ⋅ Msm + S 2 ⋅ α 2 ps ⋅ ( T 2 s - Tvo ) ⋅

⋅∆τ= Msm ⋅ csm ⋅ ∆Tsm, где Gp – массовый расход пара; Gv – массовый расход воды; I – энтальпия пара; Tk – температура конденсата на выходе теплообменника; Tv – температура воды на выходе теплообменника и входе резиносмесителя; Tvо – температура воды на выходе резиносмесителя и входе теплообменника; ck, cv, cs, csm – теплоемкости конденсата, воды, стенки и резиновой смеси; Mk, Mv, Mvo, Ms, M2s, Msm – массы конденсата в теплообменнике, воды в теплообменнике и резиносмесителе, стенки между конденсатом и водой в теплообменнике, стенки между водой и смесью в резиносмесителе, а также смеси; Ts, T2s – среднее значение температуры стенок между конденсатом и водой, среднее значение температуры стенок между водой и смесью; S1, S2 – площади стенок в резиносмесителе и теплообменнике; αts, αps, α2ts, α2ps – коэффициенты теплоотдачи от конденсата к стенке, от стенки к воде, от воды к стенке и от стенки к резиновой смеси; N – мощность электродвигателя рабочего органа смесителя; Kp – коэффициент полезного действия привода резиносмесителя; τ – время.

Запишем уравнения (1)–(6) в виде уравнений Коши. Для этого разделим левые и правые части уравнений на Δτ, перенесем производную в левую часть уравнений, а все остальное – в правую, и получим систему дифференциальных уравнений:

dTk _ Gp • I Gk • Tk • ck Stp • ats • (Tk - Ts) dT ~Mk • ck   Mk • ck        Mk • ck’ dTv _ Gv • Tvo • cv + S • aps • (Ts - Tv) Gv • Tv • cv ;

• d r     Mv • cv        Mv • cv        Mv • cv

dTs _ S • ats • (Tk - Ts) S • aps • (Ts - Tv) , ---------- ---;

• d r        Ms • cs           Ms • cs

dTvo Gv • Tv • cv Gv • Tvo • cv S 2 • a 2 ts • (Tvo - T 2 s) -------------- ---;

• d r Mvo • cv    Mvo • cv         Mvo • cv

dT2s_S2• a2ts• (Tv-T2s) S2• a2ps• (T2s-Tvo) . --------------- ---;

• d r          M 2 s • cs              M 2 s • cs

dTsm _ N • Kp • Msm ^ S 2 • a 2 ps • (T 2 s - Tvo ) d T Msm • csm        Msm • csm

Рассчитаем динамические характеристики

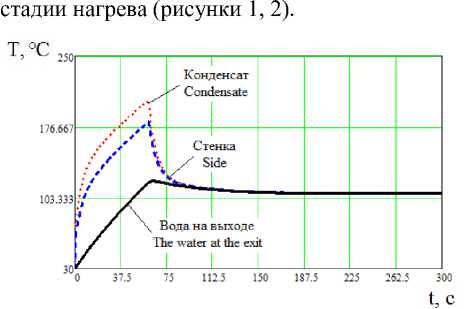
Рисунок 1. Динамические характеристики по температуре теплообменного аппарата

Figure 1. The dynamic characteristics of the temperature of heat exchanger

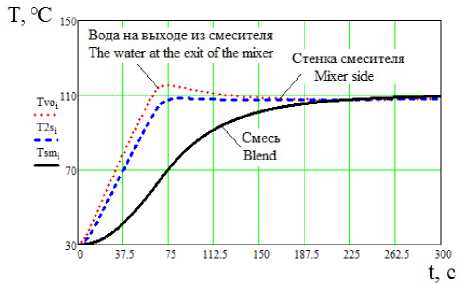
Рисунок 2. Динамические характеристики по температуре резиносмесителя

Figure 2. Dynamic characteristics by Rubber mixer temperature

Для синтеза алгоритма оптимального управления стадией нагрева воспользуемся принципом максимума Понтрягина. Задача оптимизации сводится к определению оптимального управления (подача греющего пара) и оптимальной траектории выходной координаты объекта (температура смеси), обеспечивающих минимальный расход пара при нагреве резиновой смеси за ограниченное время (при ограничении на управляющее воздействие).

Приведем уравнения системы (7) к матричной форме:

dX

----A • X + B • U + C • Z , dt

где X, U, Z – векторы переменных состояния, управления и возмущения; А, В, С – матрицы коэффициентов.

В качестве управления выступит расход пара Gp , а выделение тепла N·Kp (в результате перевода механической энергии в тепловую) станет возмущением.

В уравнениях вектор переменных состояния имеет вид { Tk Tv Tvo T2s Tsm } T ; вектор управления - { Gp о о о 0 } ^T ; вектор возмущений - { N • Kp 0 0 0 0 } ^T . Так как заведомо предполагая, что расход поступающего греющего пара Gp равен расходу конденсата, выходящего из теплообменного аппарата, то можно заметить, что система уравнений нелинейна. Но если организовать управление подачей греющего пара в двух состояниях: греющий пар подается в максимальном расходе или не подается совсем, то система уравнений (7) в каждом

из состояний управления перестает быть нелинейной. В результате мы получаем две системы линейных уравнений.				В соответствии с векторами переменных состояний запишем матрицы коэффициентов для каждого состояния управления:
	" 81D + Gk^ck		8kD	0	0	0
		Mkck	Mkck
		8kD	8k D + Gv-cv	Gv^cv	0	0
		Mv^cv	Mv^cv	Mv^cv
A1 :=		0	Gv^cv	82^a2ts + Gv	cv        82^ a2ts	0
			Mv2^ cv	Mv2^cv	Mv2^cv
		0	0	82^ a2ts Ms •cs	82^ (a2ts + a2ps) Ms •cs	82 • a2ps Ms • cs
	-	0	0	0	82^a2ps Msm- csm	82^a2ps Msm-csm	, (9)
		Skats Mk ck	Skats Mkck	0	0	0
		8kaps    81	aps + Gv cv	Gv cv	0	0
		Mv^cv	Mv^cv	Mv^cv
		0	Gv cv	S2^a2ts + Gv	cv        82^ a2ts	0
A2	•-		Mv2^cv	Mv2^ cv	Mv2^cv
		0	0	S2^a2ts	82^(a2ts + a2ps)	82^a2ps
				Ms •cs	Ms •cs	Ms • cs
		- 0	0	0	82^a2ps Msm- csm	82^a2ps Msm-csm _	.

Также з	апишем	векторы	управления
и возмущения:	^ Ipar A Mk^ ck 0	< 0 0 0
B •=	0 0 I 0 J	‘-    ■         1101 NKP ,        V cs J .

Чтобы получить математическое описание в виде зависимости выхода объекта Tsm от управления G p и возмущения N • Kp или в виде соответствующих передаточных функций, можно исключить из уравнений (7) промежуточные переменные Tk , Tv , Tvo , T 2 s и получить одно уравнение пятого порядка для Tsm . Это проще всего выполнить, переходя к преобразованиям Лапласа:

Так как уравнение записано для приращений, все начальные значения переменных равны нулю, что удовлетворяет требованиям для передаточной функций [7–9].

Из уравнения (11) достаточно найти вектор X (s), используя операции с матрицами в системе Mathcad. После нахождения передаточных функций для выхода объекта, находим корни характеристических уравнений для двух состояний управления:

( -3.3092024252193001718 A

-.50525582941656373523

Z1 :=   -.19599241914230279279

-.24858249769714896775e-1

V -.20955764521184033564e-2 J

(           0            A

-3.3092023859043633231

X ( $ , u , z ) - ( E • s - A1 ) 1 • B • u + + ( E • s - A 2 )^- 1 • C • z ,

где Е – единичная матрица; s – комплексная переменная Лапласа.

X 2 :=   -.50357336558886473926

-.16758754463218023878

v-.23707838501281881098e-1 v

Функция Гамильтона для данной системы будет выглядеть как:

H = ¥ 1 •

S 2 • a 2 ts . M 2 s • cs

Gp • I Gk • ck + Stp • a ts _ ---• Tk Mk • ck Mk • ck

¥ 3 •

+ ¥ 2 •

Gv • cv       Gv • cv + S • a ps

--Tvo---Tv

Mv • cv           Mv • cv

Gv • cv       Gv • cv + S 2 • a 2 ts        S 2 • a 2 ts

• Tv -                   • Tvo +-- T 2 s

Mvo • cv          Mvo • cv           Mvo • cv

S 2 • a 2 ts   .    S 2 • a 2 ps • ( T 2 s - Tvo )

• Tv---T 2 s--

M 2 s • cs              M 2 s • cs

+ ^

+

+

N • Kp • Msm S 2 • a 2 ps • ( T 2 s - Tvo ) Msm • csm        Msm • csm

В соответствии с принципом максимума Понтрягина оптимальное управление должно обеспечивать максимум функции Гамильтона в каждый момент времени в явном виде, т. е.

f a , если ^ b Kim >  0 u = <

[ b , если ^ 1 • Kim <  0

Поскольку все корни характеристического уравнения для стадии подачи греющего пара действительные и разные, решение его при постоянном управляющем воздействии uc можно записать как:

y ( t , C , uc ) = C 1 • e ¹⁴ + C ₂ • e^{s 2} t +

+ C ₃ • e^{s 3} t + C 4 • e^{s 4} t + C 5 • e^{s 5} t +       (15)

+ Ko • uc + Q .

Первая и последующие производные при постоянном входном воздействии равны:

dy ( t , C , n ) = C 1 • s 1 ⁿ • e^{s 1} t +

+ C ₂ • s 2 ⁿ • e^{s 2} ^ t + C ₃ • s 3 n • e^{s 3} t +       (16)

+ C ₄ • s 4 n • e^{s 4} t + C ₅ • s 5 n • e^{s 5} t .

Решение для стадии без подачи греющего пара будет иметь вид:

y ( t , C , uc ) = C 1 + C ₂ • e^{s 22} t +

+ C 3 • e^{s 33} • t + C ₄ • e^{s 44} • t +                (17)

+ C ₅ • e s ⁵⁵ t + Q .

Первая и последующие производные при постоянном входном воздействии для стадии без подачи пара равны:

dy ( t , C , n )

f C ₂ • s 22 ⁿ • e^{s 22} t + C ₃ • s 33 n • e ³³ t + C ₄ • s 44 n • e ⁴⁴ ' t + C ₅ • s 55 ⁿ • e ⁵⁵ t + Q , если n = 1; [ C ₂ • s 22 n ^ e^{s 22} t + C ₃ • s 33 ⁿ • e s ³³ t + C ₄ • s 44 ⁿ • e s ⁴⁴ ' t + C ₅ • s 55 ⁿ • e s ⁵⁵ t , если n >  1.

Для построения управления и траектории необходимо найти четыре временных точки переключения, значения пяти постоянных интегрирования С для пяти интервалов постоянства управления. Итого, необходимо найти двадцать девять неизвестных величин, составив и решив систему из двадцати девяти нелинейных алгебраических уравнений. Эту задачу можно решить только численным методом, задав достаточно близко начальное приближение неизвестным величинам. Чтобы это выполнить, приближенные значения будем задавать и уточнять последовательно (по участкам).

Примем в начальный момент управление положительным и равным а . Рассчитаем выход объекта при управлении u=uc для первого участка постоянства управления (рисунок 3) .

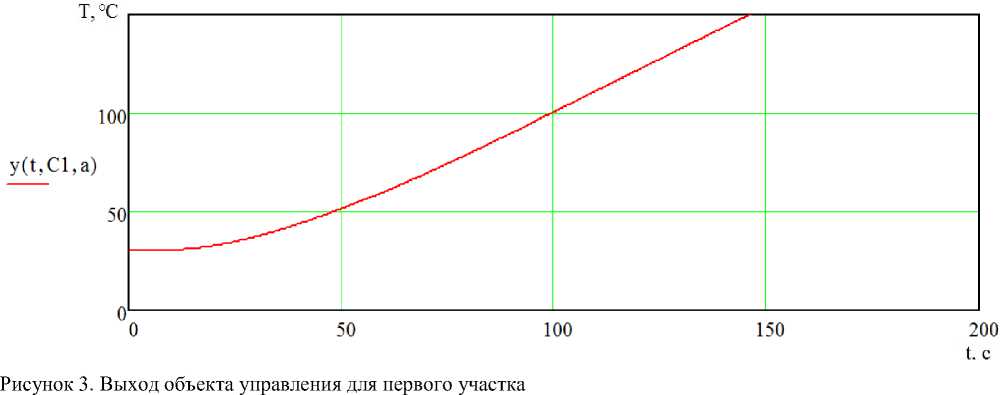
Figure 3. The output of the control object for the first section

Задавая последовательно точки переключения в пределах положительных значений у , определим начальные приближения констант интегрирования по участкам постоянства управления. Для второго участка в качестве начального приближения для констант интегрирования С2 возьмем С1 , рассчитанные для первого участка.

[ y 1 ( 1 - 1 1, C 2, b ) , если t >  t1

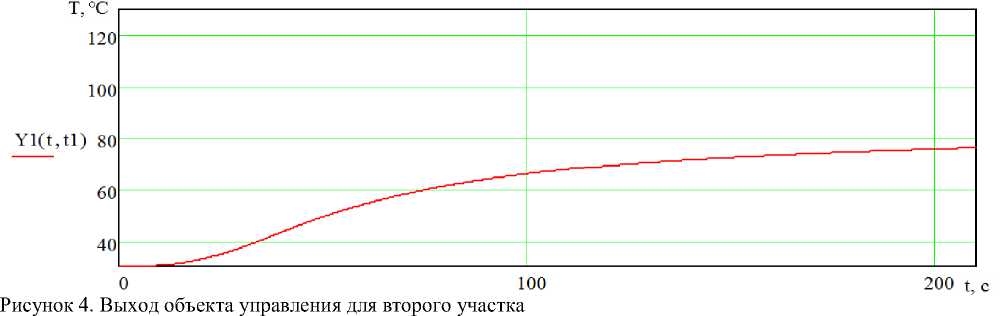
Figure 4. The output of the control object for the second section

Для третьего участка принимаем вектор констант С3=С2 . Точку переключения также задаем приближенно по графику: t2 =80.

Выражение для выхода объекта при управлении u=uc для третьего участка будет иметь вид (рисунок 5) :

Выражение для выхода объекта при управлении u=0 для второго участка будет иметь вид (рисунок 4) :

_{z 4}    f y ( 1 , C 1, a ) , если t <  t1

Y 1 ( t , 1 1 ) = 1    /

Для четвертого участка принимаем вектор констант С4=С3 . Точку переключения также задаем приближенно по графику: t3 =85.

Выражение для выхода объекта при управлении u =0 для четвертого участка будет иметь вид (рисунок 6) :

Y 2 ( t , t 1, t 2 )

Y 1 ( t , 1 1 ) , если t <  t2

y ( t - 1 2, C 3, a ) , если t >  t2

, _x    f Y 2 ( t , 1 1, 1 2 ) , если t <  t3

Y 3 ( t , 1 1, 1 2, 1 3 ) = ^   ,             _x                  (21)

[ y 1 ( t - 1 3, C 4, b ) , если t >  t3

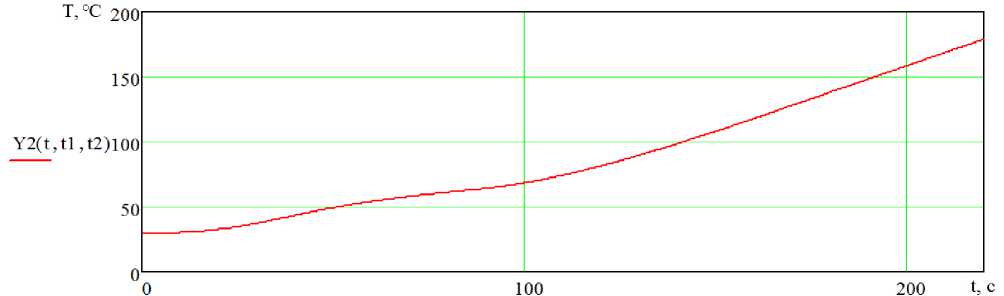
Рисунок 5. Выход объекта управления для третьего участка

Figure 5. The output of the control object for the third section

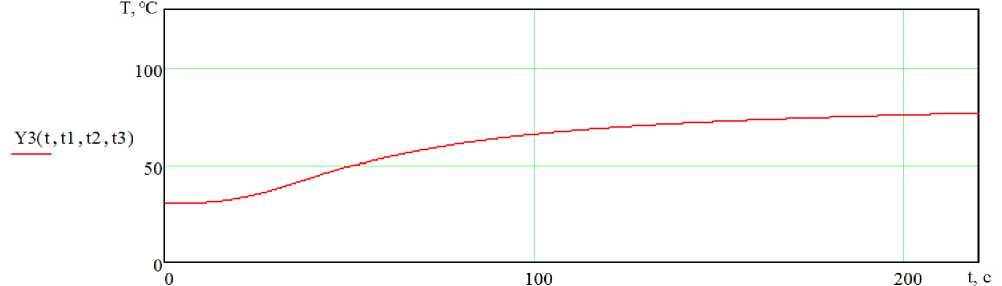
Рисунок 6. Выход объекта управления для четвертого участка

Figure 6. The output of the control object for the fourth section

Для пятого участка вновь принимаем вектор констант С5=С4 . Точку переключения также задаем приближенно по графику: t4 =100.

Выражение для выхода объекта при управлении u=uc для пятого участка будет иметь вид (рисунок 7) :

Описания координаты у и функций управления u (рисунки 8, 9) :

y ( t , C 1, a ) , если t <  t1;

y 1 ( t - t 1, C 2, b ) , если t <  t2 л t >  t1;

Y ( t ) = - y ( t - 1 2, C 3, a ) , если t <  t3 л t >  t2;

Y 4 ( t , t 1, t 2, t 3, t 4 )

Y 3 ( t , t 1, t 2, t 3 ) , если t <  t4 y ( t - t 4, C 5, a ) , если t >  t4

После этого уточняем окончательно все точки переключения, конечную точку (согласно техническому регламенту tk =130), константы для всех участков (исключая первый) и рассчитываем оптимальное управление и траекторию выхода объекта.

y 1 ( t - 1 3, C 4, b ) , если t <  t4 л t >  t3;

y ( t - 1 4, C 5, a ) , если t >  t4;

a , если t <  t1;

UU ( t ) =

b , если t <  t2 л t >  t1;

• a ,    если t <  t3 л t >  t2;

• b ,    если t <  t4 л t >  t3;

a , если t >  t4.

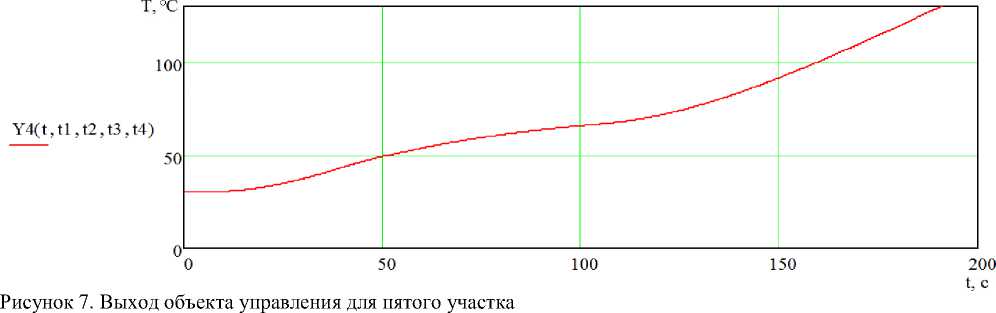
Figure 7. The output of the control object for the fifth section

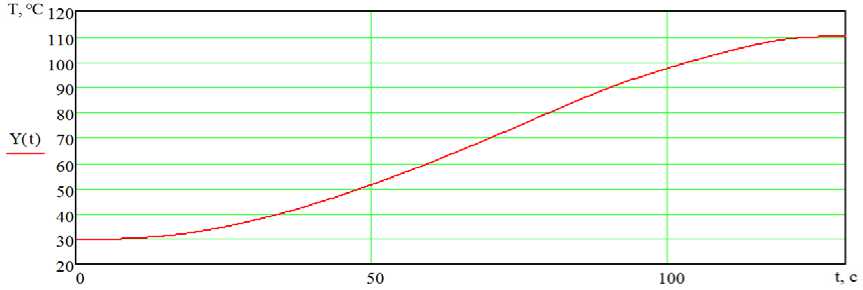
Рисунок 8. Оптимальная траектория выхода объекта управления (температура смеси)

Figure 8. The optimal path of the control object’s output (temperature of the compound)

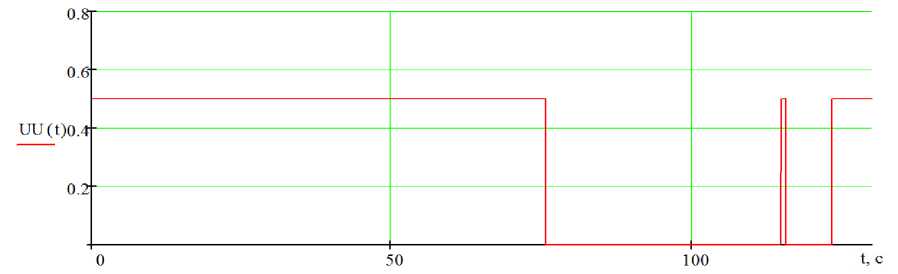
Рисунок 9. Оптимальное управление объектом (подача греющего пара)

Figure 9. Optimal control of the object (supply of the heating steam)

Сравнивая результаты (при постоянной подаче греющего пара в теплообменный аппарат и при реализации оптимального управления), установлено, что время необходимое для разогрева резиновой смеси до 110 °С при постоянной подаче пара составляет 110 с (с общим количеством поданного пара 55 кг), а при оптимальном управлении – 130 с (с общим количеством поданного пара 41,5 кг). Таким образом, экономия греющего пара составила 24,4%.

Выводы и рекомендации

Анализ результатов моделирования и проведения испытаний на предприятии при