Разработка математической модели сушки семян амаранта в аппарате со взвешенно-закрученным слоем

Процессы тепло- и массообмена в сушильных аппаратах в значительной мере определяются гидродинамической обстановкой в его внутреннем объеме. Учитывая сложность геометрии и структуры поля скорости во взвешенно-закрученном слое, которое в общем случае является существенно трехмерным, необходимо декомпозировать гидродинамическую задачу на две суперпозиционные части. Из анализа физической картины следует, что траектории линий тока близки к семейству винтовых кривых. Поэтому логично рассмотреть структуру течения в поперечных сечениях аппарата и наложить на определенную таким образом картину течения осевую составляющую, которую положить близкой к структуре идеального вытеснения.

Это правомочно допустить ввиду значительной скорости осевого потока.

Процесс сушки семян амаранта рассмотрим для одиночного семени амаранта, а затем с учетом суммирования итоговых потоков влаги для всех семян найдем макрокинетиче-ские закономерности [4].

На рисунке 1 представлена расчетная схема аппарата. Для анализа выберем цилиндрическую систему координат, расположив ось oz по оси аппарата и пренебрегая массовыми силами, тогда уравнение движения в цилиндрических координатах (г, 6, z) запишется в виде (1) с учетом постоянства плотности сушильного агента р и его динамической вязкости ^ :

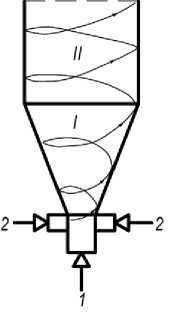
Рисунок 1. Расчетная схема: 1 - осевая подача теплоносителя; 2 - тангенциальная симметричная подача воздушного потока; I - конусная часть аппарата; II - цилиндрическая часть аппарат

( ди     ди и ди

Р —- + и —- + —--- +

V д t        д r    r дб

+ ^ 2

-

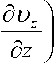
д Р

д r

-

¹2(„ ) + ¹ ®т» r д r   ^rz r дб

дт zz дz

а уравнение неразрывности:

1 д        1 ди  ди

--( r u _r ) +-- ^б + — z- = 0,       (4) r д r       r дб   д z

где   и , и_б , и  - компоненты радиальной,

ди   ди и ди

—r_ + и —- + —--- дt      дr r  дб

- 4+

r

угловой и осевой скорости соответственно; т - тензор напряжений, компоненты которого для неньютоновских жидкостей таковы:

+ и

-

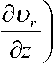
д Р

-

д r

¹ ^( r ^T rr ^{) +} (1)

r д r

_пди 2z х ^т" =" ^ [ ²17 ^- 3 ^(VU )

1 ^дт б    ^Т бб    ^дT rz

1 r дб r д z

ди   ди U ди ии

Р ^б + и ^б + — • ^б + ^ ^ +

V д t        д r    r    дб      r

+ U

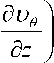
1 д Р r дб

1 д / ₂

—  (r тб r  д r

) + (2)

^Т 99 = -б

1 ди  дц. )

--^б + —- I r дб   д r )

- 2 ( V-U ) ] ;

^T zz =А ^{2 д}Ц ^- 1 ^{(V U} ")

^т г б = ^т б г = ^- б

^™

₊ ^{1 дт} 99 r дб

Т99 , дт9z r    дz

д ( и ^  1дц r — I — I + — дr V r ) r дб

( ди  1 ди I

^T 9 z = ^T z 9 =-б\ — + - — I; V д z   r дб )

( ди  ди I

^T rz = ^T zr =^-б\ — ⁺ — I; V д r д z )

„ _  1 д /   \  1 д и  ди

V-u = --( r u r ) +--- + —-   (11)

r д r       r д-   д z

При стационарном течении семена амаранта двигаются по кольцевым траекториям и компоненты скорости и_г и и равны нулю. Кроме этого считаем, что течение теплоносителя стационарное и градиенты давления вдоль координаты - отсутствует. В этом случае все члены уравнения (4) равны нулю, а (1) - (3) с учетом (5) - (11) принимают вид:

Поэтому среднее значение будет:

!    1 f 'я

Ue = - ^ие^{д r} =

r

¹ 0

w o r o 1 r ^{3 2}

2 r1    1 r r = -WO—.

10  2/1

Осевая составляющая скорости и / находится (считая потери на сопротивление потоку несущественными) из формулы:

Р - S 1 ,

-

Р^и =

r

-

дР. д r ’

где G_n - массовый расход через осевой подаю

n d 1 д / х

⁰=т т^{( r u} - ) ; dr r д r

;

0 =

—

д P д z

•

Общее решение (13) таково

» . = ¹ rC + ¹ C 2 , 2       r

щий патрубок; S j - площадь поперечного сечения цилиндрической области II .

Из (17) и (18) следует оценка скорости движения сушильного агента в цилиндрической области сушильного аппарата:

и = РмР +W ² =

где N_x и 7₂ - константы интегрирования, требующие интегрирования, они могут быть найдены из условий: при r =0 для сохранения физичности С ₂ =0; при r = r ( r_o - радиус поперечного сечения) и₆ = w _f ( w_f - скорость тангенциального потока, которая определяется как:

w, = Go^- ,

0 р - s где G - массовый расход тангенциального потока, S - площадь поперечного сечения закручивающего патрубка), тогда скорость будет r                   „

U = w o

•

< r o )

Пусть r_o - входной радиус области I , а r - радиус цилиндрической области (считаем, что входная область аппарата представляет собой правильный усеченный конус), тогда скорость в тангенциальном направлении при входе в цилиндрическую часть II будет:

‘

Г Л r

^и е = W - .

X r 1 )

Значение w, найдем из уравнения: сохра- rowo wl =-----,

r нения, то есть:         1

тогда:

^w o ^r o ^r

U- =    2  , rl

¹ w o r o

\ 12 r

)

+

G

_np r _

,

по которой можно рассчитать локальные значения коэффициентов тепло- и массоотдачи.

Расчет процесса сушки выполним из следующих соображений. Будем рассматривать этот процесс для семени амаранта, считая его форму близкой к сферической. Затем с учетом суммиро-

вания итоговых потоков влаги для всех семян найдем макрокинетические закономерности.

Для этого вначале на основе линейной термодинамики явлений переноса в капиллярно-пористых телах обобщенная система дифференциальных уравнений диффузионнофильтрационного тепло- влагопереноса записывается в следующем виде [5]:

— = a V ² u + ( a ^T _ml + a ^₂ ) v ² 1 + k p- V ² p ; (20) m           m 1      m 2

^дт                          P o

д t дт

*

Г

r ^£ w2

=--- a m V u + a_

, ___ *

+ s r

c

X

q

+

*

s r

a

m

c

S V ² 1 + )

a m S p V ² p ; c

^д Р =-^ a m- V 2 u - ^ a m- S V 2 1 + ^дт      c p          c p

^{+ a}, X

^{s a}m S p

c p

V ² p ,

где u - влагосодержание, кг/кг; t - темпера

тура, К; p - давление влажного воздуха, Па;

т - время, сек.; a_m - коэффициент диффузии

влаги во влажном материале, м²/с; К р - коэффициент фильтрационного переноса влаги; р - плотность материала, кг/м³; r - удельная теплота испарения жидкости, Дж/кг; с - удельная теплоемкость частиц материала, Дж/(кг·К); d - коэффициент температуропроводности частиц материала, м²/с; £ - коэффициент, характеризующий отношение потока жидкости и пара при нестационарном влагопереносе, £ = d_m1 / a m , d m 1 - коэффициент диффузии парообразной влаги во влажном материале, м²/с; 5_р = К_р /( a_p • р ) - относительный коэффициент фильтрационного потока влаги; a_p = Кр /( с_р • Р ) - коэффициент конвективной фильтрационной диффузии, м²/с; п_р - коэффициент емкости влажного воздуха, Id ¹; V ² - оператор Лапласа.

Будем считать, что на распределение вла-госодержания и температуры внутри частицы давление не оказывает существенного влияния ввиду малоинтенсивности процесса сушки. Поэтому система (20)-(22) упростится до вида:

Уравнения (23)-(28) образуют математическую модель.

В силу интенсивного перемешивания семян амаранта в аппарате будем считать поверхность семени равнодоступной для тепловых и массовых потоков, поэтому можно рассматривать математическую модель в зависимости от одной радиальной координаты. В этом случае в координатном виде система (23), (24) будет выглядеть:

д и

— = a дт ‘

^{+ ( a}, 1

д t дт

^д ² и 2 д и

--у +--+

(д r2   r д r J т /д2t 2д t)

⁺ a m 2 ЬТТ ⁺ "^

(д r   r д r J

m

;

I p = a m ^{v 2 u +(} a m i + a m 2 ^{)v 2} t ; д т

*

r £

=---a

m

c

*

\

£r „

⁺-- a m ⁵

^C     J

^д ² и   2 д и )  /

++ (

(д r ²    r д r J  ^V

Га ² 1   2 д t )

+ --7 +--

₍д r²   r д r ₇

;

.a q ⁺

где r - текущий радиус частицы дисперсного материала.

Начальные условия примут вид:

и ( r ,0 ) = и_о , t ( r ,0 ) = t_o ;

Условия симметрии будут выглядеть:

д t дт

*

г

*

д и ( 0, т )    д t ( О, т )

-------=------= О.

= r £ a m V ² и + a q + ^£^a m 5 V ² 1 (24)

(

c

J

К системе (23), (24) добавляются начальные условия:

u|    = u ₀ , t|    = t₀

I т = 0       ⁰’   т = 0      ⁰

где u ₀, t₀ - начальное влагосодержание и температура частиц материала. Условия симметрии частицы из-за сферической симметрии:

V и\ОО = VАОО = 0

Граничные условия теплообмена на поверхности частицы:

- Л q ( V t ) n + j_q ( т ) - (1 - £ ) r * j m ( т ) = 0, (27) где Л - теплопроводность семян амаранта; j_q ( т ) - плотность теплового потока через поверхность семени амаранта за счет конвективного теплообмена с окружающей средой; j_m ( т ) - плотность потока массы влаги через поверхность семени амаранта.

Граничное условие массообмена на по-

верхности семени амаранта:

Л ( V u + SV t )| , + j m ( Т ) = О,

где Л - массопроводность семян аммаранта.

д r

д r

С учетом того, что тепловой и массовый потоки по определению есть соответственно:

jq ^{( т} ) = ^a q ( tc ^- t n ) ^jm ^{( т} ) = ^a m ^{( u}n - ^Uc ) , где a - коэффициент теплоотдачи от окружающей среды к поверхности семени амаранта; t_c - температура дисперсной среды; t„ - температура поверхности семени амаранта; a_m - коэффициент теплоотдачи от поверхности семени амаранта к окружающей среде; и_п - влагосодержание поверхности семени амаранта; и_с - влагосодержание окружающей среды; то условие (27) примет вид:

—

—

1 ^д t ⁽ r o ^{, т} ) '

^{( 1 - £ )} rX;

⁺ « q ^{[ t}c - t ⁽ r o ^{, т )]}-

[ u ( r o ^{, т} ) - u_c ] = О,

л,

а условие (28)станет:

"^{6 и (} r o ^т ) + 5 f t c r o ^ rl"

д r

д r

+

⁺ « ж [^{U (} r o ^{, т )- U}c ^] = ⁰.

Система уравнений (29)-(34)

образует

окончательный вид математической модели конвективной сушки сферического семени амаранта.

Запишем систему (29)-(34) в безразмерном

виде с помощью относительных переменных:

г          a_aт    , X    [ t ( гт ) - L I

R = -; Fo = ^ ; T ( R , Fo ) = ^{L V,} oo ¹;

Г о          - 02                 Vc — t o )

a t (1 Fo) dR

+ Biq [1 - T (1, Fo )]-

- ( 1 - 8 ) Bi m KoLu [ U ( 1, Fo ) - 1 ] = 0,

U ( R , Fo ^fcM- u J, ^{( u}c — ^uo )

То есть:

a u __L a Fo ” ^u

( а^т

+ LuPn —7 +(ay?2

■

r ar )

2 a t )

+

R dR )

;

d T d Fo

FeLu ( d ² U 2 d U )

Pn

+ ( 1 + FeLu

+

+

+

;

ar

5 U (1F ) + Pn ar

d T (1, Fo) + dR

где Lu = a_m I a_q - критерий Лыкова, характеризующий отношение скоростей переноса массы и тепла диффузией; Pn = J ( t_c - t_o )I( u_c - u_o ) - критерий Поснова, характеризующий отношение термодиффузионного переноса влаги к диффузионному переносу; Fe = 5 r * г I c - критерий Федорова, характеризующий отношение теплосодержания переносимой жидкой и парообразной влаги к теплосодержанию высушиваемого материала; Bz' = a r I X - теплообменное число Био;

q qo q

Bi_m = a r / X - массообменное число Био;

*

^Ko = r ⁽ u c ^- u o ) ^{|( c}p ⁽ t c ^- t o )) - критерий ^Кос-совича, характеризующий зависимость между количеством теплоты, затраченным на испарение жидкости и на нагревание влажного тела.

Предлагаемая математическая модель позволяет проводить расчет процесса сушки, а также получать кривые процесса сушки семян амаранта во взвешенно-закрученном слое. Данная модель базируется на фундаментальных уравнениях А. В. Лыкова, описывает тепло- вла-гоперенос в капилярнопористых средах в линейном термодинамическом приближении учитывая конвективный способ подвода теплоты и ма-

лые размеры высушиваемого материала.