Разработка математической модели возбуждения высокочастотных осевых вибраций корпуса комбинированного насоса c шестеренным качающим узлом

• ¹    Самарский государственный аэрокосмический университет

• ²    Институт акустики машин

В статье исследуются причины повышенных осевых вибронагрузок комбинированного насоса, включающего подкачивающую шнекоцентробежную и основную шестеренную ступень. Представлена разработанная математическая модель. Проведен расчет осевых сил с целью исследования влияния осевых сил на подшипниковый узел насоса, действующих в шестеренной ступени.

Надежность и работоспособность авиационного двигателя во многом определяется функционированием его систем и, прежде всего, системы топливопитания и регулирования. Наиболее нагруженным элементом такой системы является насосный агрегат. Качающие узлы данных агрегатов являются, с одной стороны, основными источниками колебаний давления и вибраций не только системы топливоподачи, но и коробки приводов агрегатов в целом. С другой стороны, топливные насосы сами испытывают значительные динамические перегрузки. В настоящей работе исследуются причины повышенных осевых вибронагрузок комбинированного насоса, включающего подкачивающую шнекоцентробежную и основную шестеренную ступень (рис. 1).

Интенсивное осевое вибронагружение ротора подкачивающей ступени вызывает повышенный износ подшипникового узла насоса.

Установлено, что основным источником осевых вибронагрузок является шестеренная ступень агрегата. Существенному увеличению переменных осевых сил в зоне зацепления шестерен способствует несимметричная (в осевом направлении) гидравлическая разгрузка запертого объема, обусловленная наличием подвижного и неподвижного подпятников.

Гидравлическая компенсация торцевых зазоров с применением подвижного подпят- ника сокращает утечки, а следовательно, и повышает объемный к.п.д., а также сохраняет к.п.д. неизменным в течении длительной эксплуатации насоса. Гидравлическая компенсация обеспечивается за счет поджатия торцов подпятников к торцам шестерен при помощи жидкости, подводимой с линии нагнетания.

Подвижный подпятник меняет свое положение в зависимости от давления в шестеренной ступени и тем самым, при изменении давления, вызывает высокочастотную осевую вибрацию. Высокочастотная вибрация от подвижного и неподвижного подпятников передается на корпус через подшипники, и далее происходит вибровозбуждение ротора подкачивающей ступени.

Рис. 1. Конструктивная схема комбинированного насосного агрегата:

1– корпус; 2 – шнек; 3 – центробежное колесо;

4 – шестеренная ступень; 5 – привод; 6 – датчик

На рис. 2 представлен спектр вибрации на фланце подвода топлива при разных давлениях на выходе из шестеренной ступени.

Силовой анализ работы шестеренной ступени и процессов, проходящих в зоне защемления, показал, что основной причиной высокочастотной осевой вибрации является нескомпенсированность осевых сил, действующих со стороны рабочей жидкости на подвижный и неподвижный подпятники. Исследования показали, что процессы происходящие в запертом объеме носят импульсный характер. Подвижный подпятник, за счет наличия демпфирующей полости, несколько позже подвергается воздействию осевой силы. Отсутствие демпфирующей полости привело бы к одновременному восприятию осевой силы подвижным и неподвижным подпятниками в противоположных направлениях (Fл/Fпр) (рис. 3). Необходимость наличия демпфирующей полости приводит к временной нескомпенсированности. Разрабатываемая модель учитывает нескомпенсирован-ность сил по времени.

С целью исследования и уменьшения влияния осевых сил на подшипниковый узел насоса был проведен расчет осевых сил, действующих в шестеренной ступени, с рядом допущений:

Торцевой зазор принят постоянным по всей поверхности, что в действительности нарушается биением соприкасающихся тор-

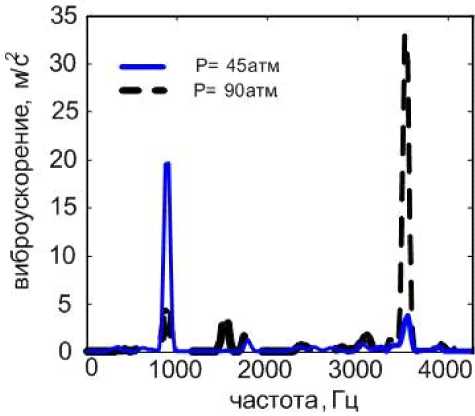
Рис. 2. Спектры вибрации на фланце подвода топлива при различных давлениях

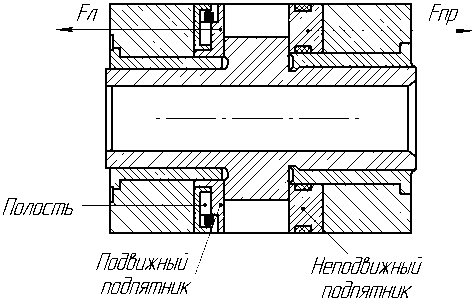
Рис. 3. Схема действия осевых сил на подпятники цевых поверхностей шестерен и уплотняющих деталей и неточностью изготовления этих плоскостей.

Давление нагнетания достаточно велико и влияние вращения одной из торцевых плоскостей с угловой скоростью щ на величину давления в зазоре незначительно, что подтверждается экспериментальными данными при давлении нагнетания около 100 атм.

Изменением давления во впадине зуба в радиальном направлении пренебрегаем. В действительности такое изменение имеет место за счет центробежных сил инерции вращающихся частиц жидкости, а также вследствии утечки жидкости в радиальном направлении через торцевой зазор. Этим градиентом давления можно пренебречь, вслед-ствии его малого значения.

Учитывая ламинарный характер течения жидкости в узких щелях, давление в направлении течения от периферии к центру падает от Рнагн до Рвс по логарифмическому закону.

Значения геометрических и режимных параметров качающего шестеренного узла, принятых в расчетах, приведены в табл. 1.

Давление разбивается на три зоны (рис. 4): 1-я - зона полного давления нагнетания Рнагн ( ψ =90°);

• 2-я - переходная зона от нагнетания к всасыванию, где давление падает от Рнагн до Рвс пропорционально углу ( ϕ =180°);

• 3-я зона давления всасывания Рвс ( χ =90°);

Каждая зона, в свою очередь, разбивается на два участка:

• 1-й участок, ограниченный радиусами головок Rе и впадин Ri, т.е. участок, охваты-

• Таблица 1. Основные геометрические и режимные параметры качающего шестеренного узла

  № п/п	Геометрические параметры	Значение
  1	Число зубьев z	11
  2	Модуль зацепления т, мм	6
  3	Зазор по спинкам зубьев, мм	0,5
  4	Ширина шестерни b, мм	21
  5	Диаметр окружности головок De , мм	84
  6	Диаметр начальной окружности D, мм	72
  7	Диаметр делительной окружности DДЕЛ, мм	66
  8	Диаметр основной окружности Do, мм	62
  9	Диаметр окружности впадин Di, мм	57,9
  10	Межцентровое расстояние А, мм	72
  11	Угол зацепления α , град	30,527
  12	Угол зацепления по вершинам зубьев αe , град	42,4
  13	Угол дуги по начальной окружности φгеом, град	15,966
  14	Высота зуба h, мм	13
  15	Шаг зацепления по основной окружности t0, мм	17,7
  16	Толщина зуба у вершины, мм	1,9
  17	Коэффициент перекрытия ε	1,1338
  18	Радиальный зазор в запертом объеме, мм	1,04
  19	Минимальный радиус контакта r2, мм	20
  20	Угол зоны полного давления нагнетания ψ, град	90
  21	Угол переходной зоны от нагнетания к всасыванию φ, град	180
  22	Угол зоны давления всасывания χ, град	90
  23	Давление нагнетания Pнагн, МПа	10
  24	Давление всасывания Рвс, МПа	1
  25	Частота вращения n, об/мин	4800
  26	Круговая частота ω, 1/сек	502,6

вающий высоту зуба, на котором давление принимаем постоянным;

2-й участок, ограниченный радиусами впадин Ri и минимальным радиусом контакта r2, на котором давление падает по логарифмическому закону.

F 1 = ^р Н^АГн •^V , ( Re² - Ri² ) .

стке

Сила давления жидкости на втором уча-1-й зоны:

(

I

Задаем P(t) = to-t                  (1)

Сила давления жидкости на первом участке 1-й зоны [1]:

F 2

РНАГН " V

Ri

2 Ri² - r2 2

к

2-lnIR I к r2 J J

. (3)

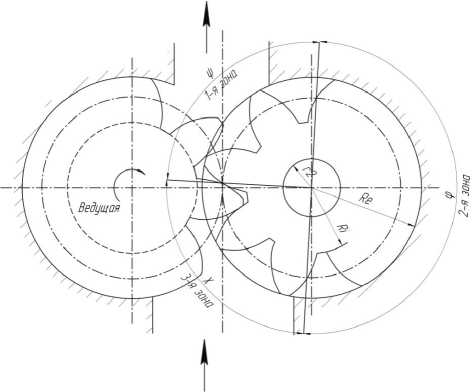
Рис. 4. Схема разбиения шестерен на расчетные зоны

Значение суммарной силы для 3-й зоны определяется по формуле:

FIII = F5 + F6.(10)

Полное значение силы определяется (рис. 5):

Fпoлн = FI + FII + FIII.(11)

Угол запертого объема рассчитывается по формуле:

2 ■ n ezap = —— •(£ -1) .(12)

Площадь одного рассматриваемого элемента:

Значение суммарной силы для 1-й зоны определяется по формуле:

FI = Fi + F2.(4)

Сила давления жидкости на первом участке 2-й зоны:

,.                   z . Re2- Ri2

F3(t) = РНАГН ■ Ф(О ■     4•

Сила давления жидкости на втором участке 2-й зоны:

S = Pzoh ^ ( Re² - Ri 2 ) + pzoh ^ ( Ri 2 - r2 2 ) ,

(13) где угол одного межзубового объема

ezah = и .

(               A

, _x P     ■ ®(t)

НАГН

F 4 (^t) =        3

Ri2

-

Ri² - r2²

Для построения математической динамической модели шестеренной ступени предполагаем, что осевая сила, действующая на неподвижный подпятник, описывается следующей зависимостью:

Для первого зуба (рис. 6):

_ . I Ri I

2 ■ ln\ — I

I r2 ))

Значение суммарной силы для 2-й зоны определяется по формуле:

F(t) =

( ^РНАГН  ^РвС ) ■ S ■ e (t) + Р ВС . S

ϕ

FII(t) = F_$(t) + F₄(t) .     (7)

Сила давления жидкости на первом участке 3-й зоны:

F 5 = ^PbCL ^ ^X ■ ( Re² - Ri 2 ) .       (8)

Сила давления жидкости на втором участке 3-й зоны:

(                A

F 6

РВС ■ X

■

Ri2

Ri2 - r22

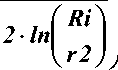
НАГН S

(P  ■ S - Fr)■ 2              (P ■ S - Fr )■ 2 , x lL_ ■ e (t) + Fe -     —У— ■ (Ф+ф)

βZAP                       βZAP l Рве ■ S

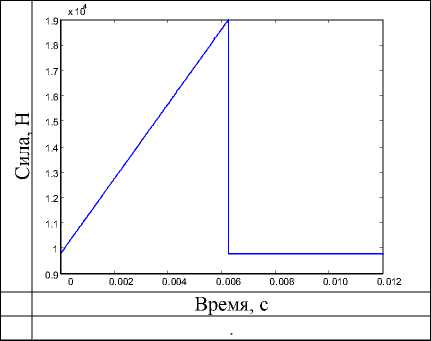
Рис. 5. График полной силы

Время, с

Рис. 6. Осевая сила первого зуба, действующая на неподвижный подпятник где Fe - k ■ Рнагн ■ ^ ,(16)

предполагаемый скачок осевой силы в момент образования запертого объема; k=4.

Для второго зуба (рис. 7):

e2(t) = e(t) + A,(17)

где межзубовый угол A - (18)

Время, с

Рис. 7. Осевая сила второго зуба, действующая на неподвижный подпятник

F2(t) -

⁽ Р нАгн  ^РВ^С ) ■ ^S ■ e 2(t) + Р ВС . S

ϕ

^РНАГН ■ ^S

⁽ Р ве ■ S - F e У 2

β ZAP

■ e 2(t) + F e -

⁽ Р ве ■ S - F e ) • 2

β ZAP

^фФ ⁺ V )

^Рве ■ ^S

^{( Р}нлгн ^{- Рве} ) ■ ^S ■ e 2(t) + Р ВС . S -Г ^{( Р}Н^{лГН - Рве} ) ■ ^S . ^> + V + x ) ф                        L ф                  .

Fsu^m(t^{) -} 2 F i ^(t) .     (20)

i - 1

Для подвижного подпятника вводим учет временной задержки Дt=0,000284с (четверть времени существования межзубового объема)

t1(t) - t + At ,          (21)

es(t) - №■ t1(t) .       (22)

Осевая сила, действующая на подвижный подпятник, описывается следующей зависимостью:

Для первого зуба (рис. 9):

Fs(t) -

Аналогично для остальных зубьев смещение на Д.

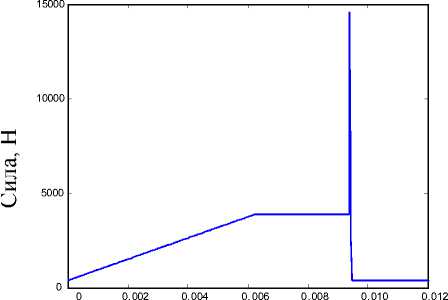
Суммарная осевая сила, действующая на неподвижный подпятник (рис. 8):

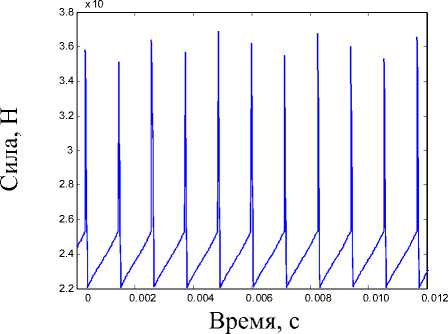
Рис. 8. Суммарная осевая сила, действующая на неподвижный подпятник

( ^РНАГН ^Рве ) • ^S . es(t) + Р ВС . S

ϕ

НАГН

( Р_в,. ■ S - F_B ) ■ 2                 ( Р_в,. ■ S - F_B ) ■ 2 ,      .

. es(t) + F e -           ^e-F_ . ( ф + V )

β ZAP                        β ZAP

. Р ве ■ S

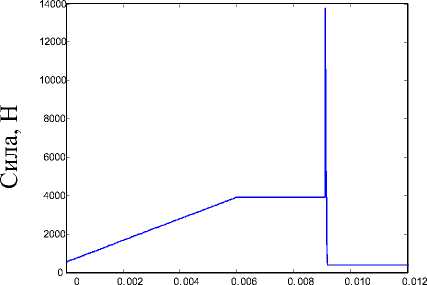
Время, с

Рис. 9. Осевая сила первого зуба, действующая на подвижный подпятник

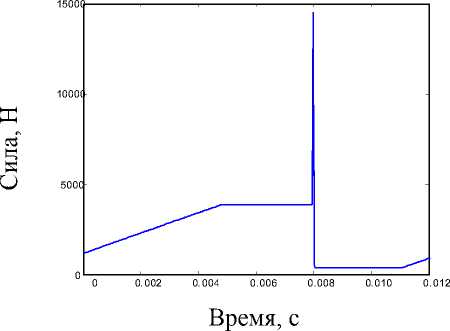
Рис. 10 . Осевая сила второго зуба, действующая на подвижный подпятник

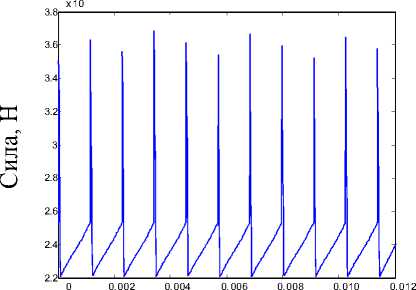
Время, с

Рис. 11 . Суммарная осевая сила, действующая на подвижный подпятник

Для второго зуба (рис. 10):

Аналогично для остальных зубьев сме-

F2s(t) =

e2s(t) = es(t) + A ,       (24)

^{( р} НА ^{гн Р} ВС ) • ^S . e 2s_(t) + р ВС • s ^ϕ

^РНАГН • S

( P bc • S - F e ) • 2

β ZAP

• ^e 2s(t) + F e

-

( P bc • S — F e ) • 2

β ZAP

•⁽ 9 ⁺ V )

P bc • S

^{( Р} Н ^{АГН - Р} ВС ) • ^S • e 2s(t) + Р ВС . S -[ ^{( Р} Н ^АГН — ^Pbc ) • ^S . ^> + V + X )

9                         L 9                  _

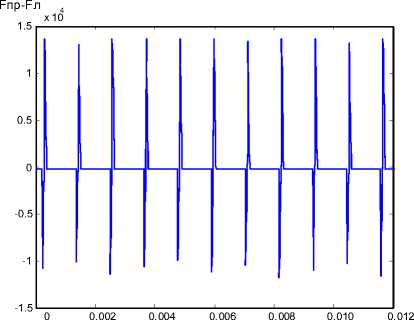
щение на Д.

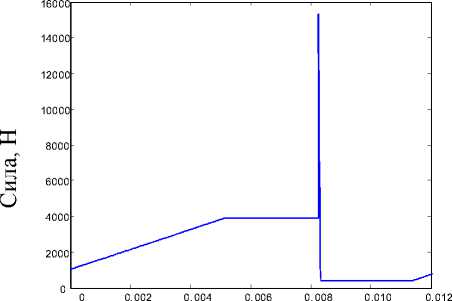
Суммарная осевая сила, действующая на подвижный подпятник (рис. 11):