Разработка математической модели зависимости удельного объемного электрического сопротивления изоляции СИП-4 от факторов, влияющих на ее надежность

DOI:

Денисов И. В. Разработка математической модели зависимости удельного объемного электрического сопротивления изоляции СИП-4 от факторов, влияющих на ее надежность. Вестник МГТУ. 2024. Т. 27, № 4. С. 501–510. DOI:

Denisov, I. V. 2024. Development of a mathematical model of dependence of specific volumetric electrical resistance of SIW-4 insulation on factors affecting its reliability. Vestnik of MSTU, 27(4), pp. 501–510. (In Russ.) DOI:

Как один из способов повышения безотказной работы оборудования, используемого при передаче электрической энергии и электрических проводников, следует рассматривать методики, имеющие возможность прогнозировать остаточный ресурс. Полученные результаты оценки остаточного ресурса позволят применить к соответствующему оборудованию или упреждающий ремонт или его замену, чтобы не допустить отказа функционирования. При написании научной работы автором статьи были рассмотрены модели старения изоляции Журкова, Крайна, модифицированная модель старения изоляции проводов, основанная на законе Аррениуса и обратной степенной модели, а также модель старения изоляции Г. С. Кучинского, которая учитывает два основных фактора – температуру и электрическое поле ( Дубяго, 2021; Поляков, 2017 ). Однако большинство рассмотренных моделей не имеют возможности косвенного определения остаточного ресурса, используя для этого, к примеру, параметры работоспособности системы, такие как сила тока, напряжение, мощность, температура и т. д. Это затрудняет их использование в реальных эксплуатационных условиях. Использование предлагаемой автором методики прогнозной оценки остаточного ресурса материала изоляции СИП-4 позволит посредством разработанной математической модели осуществить мгновенную оценку значения удельного объемного электрического сопротивления изоляции и скорректировать ее безопасную эксплуатацию по времени.

В статье рассматривается один из этапов реализации предлагаемой методики, а именно результаты проведения полного факторного эксперимента, в процессе которого получена математическая зависимость удельного объемного электрического сопротивления от действия внешних факторов, таких как переменный электрический ток, температура окружающей среды и продолжительность эксплуатации.

Материалы и методы

Анализ математических моделей, дающих прогнозную оценку остаточного срока эксплуатации, позволил установить два наиболее значимых фактора – напряжение и напряженность электрического поля. Поскольку напряжение в сети составляет 230 В согласно ГОСТ 29322-20141, то варьировать им при проведении многофакторного эксперимента не имеет смысла. При потреблении электрической энергии потребители, как правило, могут увеличить мощность потребления, следовательно, электрический ток в сети увеличится прямо пропорционально. В результате анализа ГОСТа 31946-10122 и ТУ 16-705.500-20063 получена следующая информация: допустимая токовая нагрузка СИП-4 2х16, рассчитанная при температуре окружающего воздуха (среды) 25 °С, скорости ветра 0,6 м/с и интенсивности солнечной радиации 1 000 Вт/м2, составляет не более 100 А. Значение силы тока короткого замыкания при условии действия его в течение 1 с составляет не более 1,5 кА. В нашем многофакторном эксперименте мы не будем брать в расчет электрический ток короткого замыкания, так как это уже относится к разрушающим методам контроля, а воспользуемся таблицей 9, находящейся в ТУ 16-705.500-2006 (табл. 1).

Согласно табл. 1 максимальная температура, для которой представлен поправочный коэффициент, составляет 50 °С.

Таблица 1. Поправочные коэффициенты расчета электрического тока в зависимости от температуры окружающей среды

Table 1. Correction factors for calculating electric current depending on the ambient temperature

Температура токопроводящей жилы, °С	Поправочные коэффициенты при температуре окружающей среды, °С
	–5 и ниже	0	5	10	15	20	25	30	35	40	45	50
90	1,21	1,18	1,14	1Д1	1,07	1,04	1,00	0,96	0,92	0,88	0,83	0,78

В принципе, согласно пункту 6.1 ТУ 16-705.500-2006 СИП-4 допускается эксплуатировать при температуре окружающей среды от минус 60 °С до плюс 50 °С, этим объясняется отсутствие поправочных коэффициентов выше указанной температуры. Однако в пункте 1.6.4 ТУ 16-705.500-2006 написано, что изолированные провода должны быть стойкими к комплексу атмосферных факторов при их циклическом воздействии и допускаемая температура воздействия составляет 70 °С. Проведенный анализ характеристик материала изоляции провода из сшитого полиэтилена установил, что температура 90 °С является нормальной рабочей температурой данного материала, а температура в 130 °С допустима в режиме перегрузки, не превышающем 8 ч. При этом максимальная температура нагрева материала изоляции из сшитого полиэтилена в режиме короткого замыкания, не превышающем 5 с, может достигать 250 °С. На основании изложенного можно предположить, что при температуре токоведущей жилы 90 °С изоляция СИП может разогреваться также до 90 °С ввиду действия внешних факторов, таких, например, как солнечная радиация. Солнечные лучи могут разогревать материал изоляции СИП до температуры 75–80 °С. Безусловно, такой перегрев материала изоляции будет способствовать ускоренному его старению.

На рис. 1 представлены экспериментальные и теоретические зависимости поправочного коэффициента от температуры нагрева изоляции СИП.

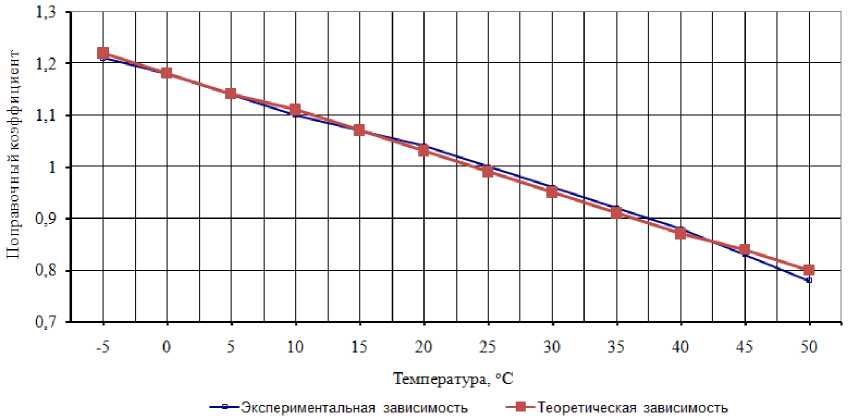
Рис. 1. Экспериментальные и теоретические зависимости поправочного коэффициента от температуры нагрева изоляции СИП

Fig. 1. Experimental and theoretical dependences of the correction factor on the heating temperature of the SIW insulation

Используя метод наименьших квадратов, получена формула теоретической зависимости вида y = kx + b :

y = - 0,00767 T + 1,1817. (1)

Используя полученную формулу зависимости поправочного коэффициента от температуры окружающей среды, можно определить допустимую токовую нагрузку. Так, для температуры окружающей среды 90 °С допустимая токовая нагрузка составляет 49,1 А, а для температуры 130 °С уже 18,4 А, что составляет эквивалент активной мощности 4,23 кВт.

Таким образом, минимально допустимая токовая нагрузка будет нами принята равной 4,0 А (нижний уровень), что соответствует 1 кВт активной мощности, а максимальная токовая нагрузка – 16,59 А (верхний уровень), что соответствует активной мощности в 4 кВт.

В пункте 6.1 ТУ 16-705.500-2006 дана информация о диапазоне температур эксплуатации СИП, она составляет диапазон от минус 60 °С до плюс 50 °С. Однако ввиду сложности проведения многофакторного анализа при отрицательных температурах условимся считать нижним уровнем температуру, равную 20 °С. Проведенный анализ верхней и нижней токовой нагрузки позволяет нам принять за верхний уровень температуру, равную 130 °С. Это максимально близко воспроизведет наиболее тяжелые условия эксплуатации, характерные для жаркого летнего периода. Именно в данный период времени происходят наиболее активные термохимические реакции разрушения молекул полиэтилена, составляющие материал изоляции СИП-4.

В исследовании использовалось 30 м СИП-4, приобретенные в магазине, также несколько десятков метров бывшего в употреблении СИП-4 было предоставлено сотрудниками АО "ОРЭС – Владимирская область". Дата производства наиболее "свежего" СИП-4 – март 2024 г., "старого" – июль 2009 г. Таким образом, нижний уровень периода эксплуатации составляет 0,16 года. Верхний уровень периода эксплуатации СИП-4 равен 14,4 года. Данный фактор позволит учесть влияние накопленной наработки, что эквивалентно приобретенным за этот период усталостным разрушениям материала изоляции от действия как совокупности атмосферных факторов, так и перенапряжения и напряженности электрического поля, которые способствовали разрушению молекул полиэтилена, а следовательно потере изоляцией диэлектрических свойств. В процессе отбора исследуемые образцы СИП-4 подвергались визуальному осмотру на предмет механического повреждения изоляции. У образцов, чей срок службы составлял 10 и более лет, на поверхности изоляции в местах закругления можно было наблюдать "паутину", что говорит об образовании мельчайших трещин, впоследствии переходящих в макротрещину (рис. 2).

Изоляция таких проводов характеризовалась повышенной жесткостью и твердостью, что говорило о снижении пластических свойств. Выполненные измерения твердости поверхности изоляционного материала дюрометром (твердость по Шору, методом вдавливания) подтверждают этот факт. Образец СИП-4 производства 2024 г. имеет твердость поверхности изоляции 44,9 HD, а образец 2012 г. 60,1 HD. Установленная повышенная твердость изоляции в последующем приведет к появлению микротрещин при воздействии циклических знакопеременных нагрузок, в дальнейшем – к образованию макротрещин, а учитывая переход через ноль при попадании в них влаги, это будет способствовать ускоренному ее разрушению и, как следствие, снижению электрического сопротивления.

Рис. 2. Снимок поверхности материала изоляции исследуемого образца СИП-4 производства 2012 года под микроскопом

Fig. 2. The surface of the insulation material of the studied SIW-4 sample produced in 2012. The photo made by a microscope

Жесткость – это способность сопротивления деформации, а твердость – способность сопротивления проникновению, но поскольку СИП подвергается механическим знакопеременным нагрузкам, это приводит к ломкости материала изоляции. Это отчетливо видно на образцах, чей срок службы переходил рубеж в 10 лет. Кроме этого, образцы, имеющие следы прокола от прокалывающего ответвительного зажима, также имели по результатам измерений меньшее значение сопротивления, что можно объяснить отсутствием у этих проводов водоблокирующего элемента. Алюминиевая жила у таких проводов имела следы коррозионного воздействия. Также в процессе визуального осмотра изоляции проводов попадались образцы, на поверхности изоляции которых находились следы химической коррозии. Удельное объемное сопротивление таких проводов было значительно меньше указанного значения по ГОСТ 31946-20124.

Для проведения линейного полного факторного эксперимента в качестве объекта исследования был взят СИП-4 2 x 16 с изоляцией из светостабилизированного сшитого полиэтилена. Измерения удельного объемного электрического сопротивления выполнялись мегаомметром МЕГЕОН 13125. Данный измерительный прибор позволяет выполнить замеры сопротивления изоляции проводов при испытательном напряжении от 100 до 2 500 В, при этом диапазон измеряемого сопротивления составляет от 100 кОм до 50 ГОм. Погрешность измерения сопротивления ±8 % (для диапазона 100 кОм – 10 ГОм) и ±10 % (для диапазона 10–50 ГОм). Для определения температуры материала изоляции подконтрольных образцов при проведении линейного полного факторного эксперимента будет применен бесконтактный инфракрасный термометр Benetech GM320, имеющий диапазон измерения температуры от минус 50 °С до плюс 400 °С. Точность измерения прибора составляет ± 1,5 °С в диапазоне 0 ~ +400 °С; ± 3,0 °С в диапазоне –50 ~ 0 °С; спектральный диапазон 5–14 мкм.

Для проведения полного факторного эксперимента были отобраны образцы в количестве 8 штук и каждый длиной 4 м. Образцы, которые будут подвержены температурному воздействию, предварительно свернуты в бухту диаметром 220 мм. Длина образца в 4 м взята из расчета измерения сопротивления изоляции провода непосредственным погружением в воду, концы образца должны отстоять от поверхности воды на расстоянии не менее 0,5 м. В воде производились замеры удельного объемного электрического сопротивления. Испытательное напряжение прикладывалось между токонесущей жилой и водой, непосредственно контактируемой с изоляцией, что позволяло увеличить площадь контактирования и учесть невидимые глазу повреждения изоляции. Методика измерения электрического сопротивления изложена в ГОСТ 31946-20125 и ГОСТ 20.57.4066 (метод 201-1.2). Длительность воздействия температуры в 130 °С составляет 5 ч, после чего образец постепенно остывал (не менее часа) до установления температурного баланса с окружающей средой. Перед выполнением замера сопротивления каждый образец помещался в емкость с водой и находился в ней не менее 30 мин. В качестве нагрузочного сопротивления в целях безопасности проведения эксперимента были использованы тепловентиляторы с общей мощностью 2 кВт с возможностью ступенчатого регулирования. Мощность первой и второй ступени составляет 1 кВт, что в сумме дает нагрузку в 2 кВт. Последовательно в электрическую цепь был подсоединен амперметр.

Определим интервалы варьирования исследуемых факторов, а также найдем основной уровень каждого из них. Напомним, что основной уровень фактора подразумевает собой значение, под которым мы будем понимать исходное в плане проведения эксперимента. Следует отметить, что выбор значения основного уровня указанных факторов должен соответствовать получаемому значению функции отклика. Полученные значения интервалов варьирования указанных факторов, а также верхний, нижний и основной уровни приведены в табл. 2 ( Задорожная, 2018 ).

Таблица 2. Верхний, основной и нижний уровни факторов Table 2. Upper, main and lower levels of factors

**Показатели *Уровни факторов	I , А	T , °С	L , год
ВУ(max)	16,5	130	14,4
НУ(min)	4	20	0,16
ОУ = (ВУ – НУ)/2	10,25	75	7,28
ИВ = ВУ – ОУ	6,25	55	7,12

Примечание. * ВУ – верхний уровень фактора; НУ – нижний уровень фактора; ОУ – основной уровень фактора; ИВ – интервал варьирования; ** I – электрический переменный ток, А; T – температура окружающей среды, °С; L – период эксплуатации, год.

Составим матрицу планирования полного факторного эксперимента (табл. 3).

Таблица 3. Матрица планирования факторного эксперимента типа 23

Table 3. Matrix for planning the factorial experiment of type 23

Фактор	Порядок проведения опыта
	3	5	1	7	6	4	2	8
Х 0	1	1	1	1	1	1	1	1
Х 1	1	–1	1	–1	1	–1	1	–1
Х 2	1	1	–1	–1	1	1	–1	–1
Х 3	1	1	1	1	–1	–1	–1	–1
Х 1 Х 2	1	–1	–1	1	1	–1	–1	1
Х 2 Х 3	1	1	–1	–1	–1	–1	1	1
Х 1 Х 3	1	–1	1	–1	–1	1	–1	1
Х 1 Х 2 Х 3	1	–1	–1	1	–1	1	1	–1
*Параметр оптимизации
Y 1 ·1011	6,18	9,38	14,9	13,22	11,52	12,79	16,64	17,06
Y 2 ·1011	6,39	8,95	14,5	13,65	11,94	12,37	15,78	17,49
Y 3 ·1011	6,39	8,74	14,9	13,65	11,94	13,22	16,64	17,06
Y ·1011	6,32	9,03	14,7	13,51	11,80	12,79	16,35	17,20

Примечание. * Значения параметра оптимизации (функции отклика) представлены в виде удельного объемного электрического сопротивления (размерность Ом·см) из расчета D = 7,7 мм; d = 4,6 мм; L = 350 мм; R – текущее значение сопротивления подконтрольного участка провода, МОм.

Определим дисперсию опыта по данным n параллельных опытов

n

S 2 = — £ (Y n - Yrf,                              (2)

n - 1 n^

где n - число параллельных опытов, n = 3; Y_n - значение параметра оптимизации, полученное в результате опыта; Yj - среднее значение параметра оптимизации.

На основании проведенных расчетов получаем: S 2 = 1,51-10²⁰; S 2 = 1,06-10²¹; S 2 = 6,06-10²⁰;

S 2 = 6,06-10²⁰; S 2 = 6,07-10²⁰; S 2 = 1,82-10²¹; S 2 = 2,43-10²¹; S 2 = 6,07-10²⁰.

Определим ошибку опыта по формуле

n

S 2=] —Т £ ( Y n - Y j )².                                  (3)

• V n -1 n - 1

Получаем: S = 12,31^10 9 ; S₂ = 32,58-10 9 ; S₃ = 24,63-10 9 ; S₄ = 24,63-10 9 ; S = 24,63-10 9 ; S₆ = 42,66-10 9 ;

S₇ = 49,26-10 9 ; S = 24,63 40 9 .

Проверим однородность дисперсии по критерию Кохрена max

G p   <г² + s² + s² + s² + s² + s² + s² + s² ’                                   ⁽ )

• ^S 1 ^{+ S} 2 ^{+ S} 3 ^{+ S} 4 ^{+ S} 5 ^{+ S} 6 ^{+ S} 7 ^{+ S} 8

где S Lx - максимальная дисперсия.

Используя таблицу значений критерия Кохрена для доверительной вероятности, равной 0,95, находим G T = 0,51. Расчетное значение критерия Кохрена G p , выполненное по формуле (4), равно 0,0192, т. е. G p <  G T . Это означает, что дисперсии однородны и исследуемая величина y_n подчиняется нормальному закону распределения.

Следующим шагом будет определение дисперсии воспроизводимости

n

S V = 7 £ ^S2 ,                                     (5)

N i = 1

где N - число опытов в матрице планирования, N = 8.

Тогда S 2 = 9,86 4 0²⁰

На основании результатов проведенного эксперимента определим коэффициенты модели по формуле

N bo = N £ Yj-                                       (6)

Получим: b ₀ = 12,7340^п.

Коэффициенты регрессии, характеризующие эффекты взаимодействия, определяются по формуле

N bi =N £  ■                                        (7)

Получаем: b 1 = -4,09-10¹⁰; b 2 = -2,73-10¹¹; b 3 = -1,81-10¹¹; b 12 = -5,1640¹⁰; b 23 = Ц98-10¹⁰; b 13 = 5,33• 10⁹; b 123 = -4,8-10¹⁰.

Выполним проверку значимости коэффициентов путем сравнения абсолютной величины коэффициентов с доверительным интервалом. Дисперсию коэффициента определяем по выражению

|b 1 = 1,81-Ю¹¹ > 1,3640 10 => коэффициент значим;

|b_n | = 5,1640¹⁰< 1,3640¹⁰ => коэффициент значим;

I b 231 = 4,98^10 10 > 1,36^10 10 => коэффициент значим;

|b ₁₃1 = 5,33 409 > 1,36401 |b ₁₂₃1 = 4,840¹⁰< 1,3640

=> коэффициент незначим;

=> коэффициент значим.

Выполним проверку значимости коэффициентов с помощью t -критерия Стьюдента. Вычислим t р -критерий по выражению

t„ = p   S(bi)

.

После этого сравним его с табличным t T . Выполним расчет критерия Стьюдента по формуле (10) t_р0 = 198,58 > 2,12 => коэффициент значим;

t_р1 = 6,37 > 2,12 => коэффициент значим;

t р2 = 42,71 > 2,12 => коэффициент значим;

t р3 = 28,28 > 2,12 => коэффициент значим;

t_р12 = 8,04 > 2,12 => коэффициент значим;

t р23 = 7,76 > 2,12 => коэффициент значим;

t р13 = 0,83 < 2,12 => коэффициент незначим;

t_р123 = 7,48 > 2,12 => коэффициент значим.

Определим дисперсию адекватности по формуле

S ad

N n Ё (Yi — Y )2

i = 1

N - (k +1) ,

где k – число факторов.

Найдем Y i по полученному уравнению

Y_i = b ₀ + b ₁ X ₁ + b ₂ X ₂ + b ₃ X ₃ + b ₁₂ X ₁ X ₂ + b ₂₃ X ₂ X ₃ + b ₁₂₃ X ₁ X ₂ X ₃.

Тогда

Y 1 = 6,28·10¹¹; Y 5 = 11,85·10¹¹;

Y 2 = 9,08·10¹¹; Y 6 = 12,74·10¹¹;

• Y 3 = 14,73·10¹¹; Y 7 = 16,41·10¹¹;

• Y 4 = 13,56·10¹¹; Y 8 = 17,15·10¹¹.

Теперь рассчитаем дисперсию адекватности: S 2 = 1,7^10 20 .

Произведем проверку гипотезы адекватности найденной модели по F -критерию Фишера

F = Sad- p    Sv2 .

Если F р <  F Т для принятого уровня значимости и соответствующих чисел степеней свободы, то модель считается адекватной. В противном случае гипотеза адекватности отвергается. Для определения табличного значения F Т критерия Фишера необходимо найти значение коэффициентов f 1 и f 2 . Значение f 1 равно числу факторов, в нашем случае f 1 = 3. Значение f 2 равно N – k –1, т. е. f 2 = 8–3–1 = 4. В итоге табличное значение критерия Фишера F_Т = 6,6, расчетное значение критерия Фишера F_р = 0,173, т. е. F_р <  F_Т (0,173 < 6,6), следовательно, модель адекватна.

Результаты и обсуждение

Теперь получим окончательное уравнение удельного объемного сопротивления изоляции СИП

p = 1,274012 - 4,09 ■Ю10 ■

I - ОУ

-

ИВ

2,74■Ю¹¹ ■

T - ОУ

ИВ

-

1,81-Ю11 ■

L - ОУ

ИВ

-

-5,16-1010 ■

I - ОУ )( T - ОУ

■

-

ИВ

ИВ

4,98 - 10¹⁰ ■

T - ОУ ^( L - ОУ

■

-

ИВ

ИВ

-4,8-1010 ■

I - ОУ ^( T - ОУ ^( L - ОУ

■

■

ИВ

ИВ

ИВ

.

В табл. 4 представлены результаты расчета удельного объемного электрического сопротивления изоляции СИП в зависимости от переменного электрического тока, температуры окружающей среды и продолжительности эксплуатации.

Таблица 4. Результаты расчета удельного объемного электрического сопротивления изоляции СИП-4 Table 4. Results of calculation of specific volumetric electrical resistance of SIW-4 insulation

Удельное объемное электрическое сопротивление изоляции, Ом·см	Фактор I , А	Удельное объемное электрическое сопротивление изоляции, Ом·см	Фактор T , °С	Удельное объемное электрическое сопротивление изоляции, Ом·см	Фактор L , год
9,08·1011	4	14,73·1011	20	11,86·1011	0,16
8,63·1011	6	13,19·1011	40	10,96·1011	2,46
8,18·1011	8	11,66·1011	60	10,05·1011	4,76
7,73·1011	10	10,12·1011	80	9,15·1011	7,06
7,28·1011	12	8,58·1011	100	8,25·1011	9,36
6,83·1011	14	7,04·1011	120	7,35·1011	11,66
6,38·1011	16	5,50·1011	140	6,44·1011	13,96

На рис. 3–5 построены графики зависимости среднеарифметического отклонения удельного объемного электрического сопротивления изоляции СИП-4 от выше исследуемых факторов.

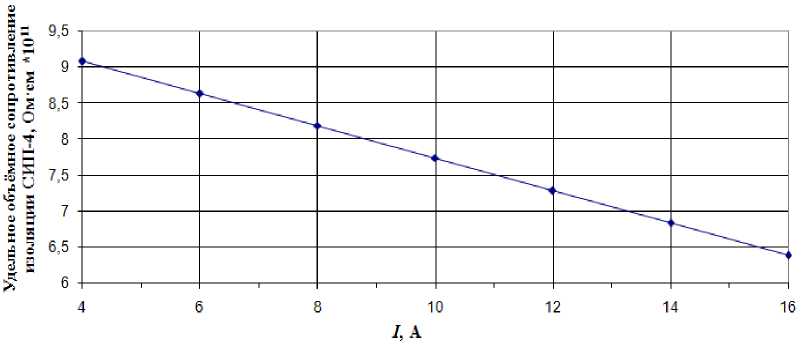
Рис. 3. График зависимости среднеарифметического отклонения удельного объемного электрического сопротивления изоляции СИП-4 от переменного электрического тока Fig. 3. Graph of the dependence of the arithmetic mean deviation of the specific volume electrical resistance of SIW-4 insulation on alternating electric current

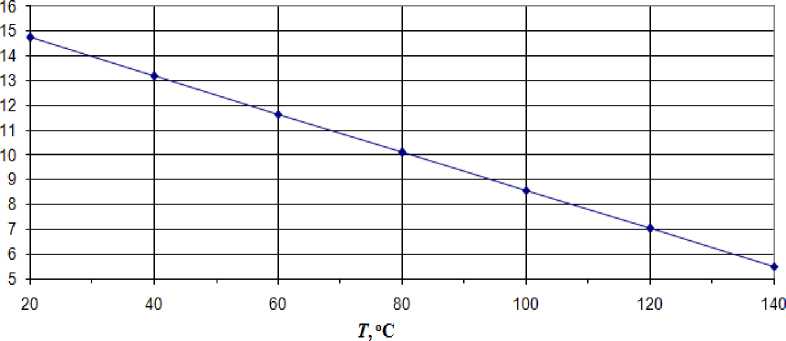
Рис. 4. График зависимости среднеарифметического отклонения удельного объемного электрического сопротивления изоляции СИП-4 от температуры окружающей среды Fig. 4. Graph of the dependence of the arithmetic mean deviation of the specific volume electrical resistance of SIW-4 insulation on the ambient temperature

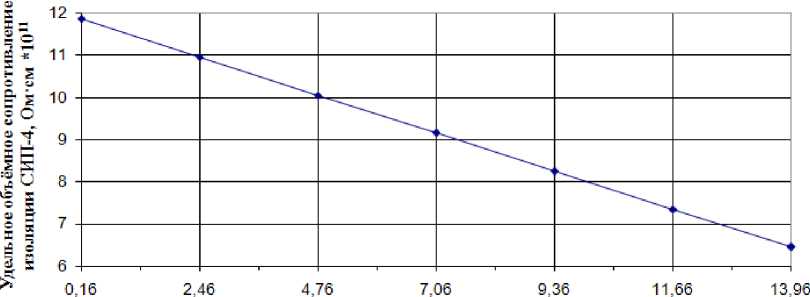
■С; ГОД

Рис. 5. График зависимости среднеарифметического отклонения удельного объемного электрического сопротивления изоляции СИП-4 от периода (продолжительности) эксплуатации Fig. 5. Graph of the dependence of the arithmetic mean deviation of the specific volume electrical resistance of SIW-4 insulation on the period (duration) of operation

На основании выполненных исследований определены верхние и нижние уровни исследуемых факторов: переменный электрический ток, НУ – 4 А, ВУ – 16,5 А; температура окружающей среды, НУ – 20 °С, ВУ – 130 °С; период (продолжительность) эксплуатации, НУ – 0,16 год, ВУ – 14,4 год (лет). Подобраны необходимые измерительные инструменты, обеспечивающие точность проведения полного факторного эксперимента. Так, для измерения сопротивления материала изоляции СИП-4 был использован мегаомметр МЕГЕОН 13125, обеспечивающий достаточную точность в измерении, для измерения температуры исследуемых образцов СИП-4 – бесконтактный инфракрасный термометр Benetech GM320, для контроля параметров переменного электрического тока – два амперметра АМА-801. Проведен линейный полный факторный эксперимент, в результате которого получена математическая модель, отображающая зависимость удельного объемного электрического сопротивления изоляции СИП-4 в зависимости от исследуемых факторов. Данная модель проверена на адекватность по F -критерию Фишера. Построены графики, отображающие зависимость среднеарифметического отклонения удельного объемного сопротивления изоляции СИП-4 от исследуемых факторов.

Заключение

В результате проведения линейного полного факторного эксперимента получена математическая модель, отображающая зависимость удельного объемного электрического сопротивления материала изоляции СИП-4 от действия внешних факторов: переменного электрического тока, температуры окружающей среды и продолжительности эксплуатации. Полученная математическая модель может быть использована для моделирования мгновенного значения удельного объемного электрического сопротивления материала изоляции СИП-4. Полученное значение удельного объемного электрического сопротивления конкретного участка СИП-4 позволит в дальнейшем принять соответствующее управляющее техническое воздействие, необходимое для обеспечения вероятности безотказной работы электрической сети на уровне 0,95, и не допустить внезапного отказа.

Автор выражает благодарность своему коллеге канд. техн. наук, доценту Максимову Юрию Павловичу за консультации по вопросам электропроводимости диэлектрических материалов в процессе подготовки и реализации плана научного исследования в области влияния эксплуатационных факторов на надежность изоляции СИП-4.