Разработка механизма расчета страховых ставок в модели заболевания сахарным диабетом

В последнее время начали широко применяться актуарные исследования в анализе рисков. Существует большое количество моделей, и одной из них является стохастическая модель Уилки. Такие модели описывают случайные процессы, в которых подразумевается, что случайность тех или иных явлений выражается в терминах вероятности. Немаловажную роль в их построении также играет и статистическое моделирование. В основе регулирования страховых отношений между страховщиком и страхователем лежат методы, опирающиеся на математические и статистические закономерности. Они и называются актуарными расчетами.

Большинство популярных приложений используют принцип, использующий марковские процессы при моделировании условий поведения системы. Это задачи с начальными статистическими данными, например, задачи системам массового обслуживания: почта, мастерские, заправочные станции, магазины и т.д. Так для представления состояния страхователя используется тот же подход.

В результате математического анализа получаем 2 противоположные задачи: прямая, где необходимо найти вероятности нахождения индивида в том или ином состоянии при известных параметрах модели и обратная, где необходимо найти параметры модели, используя известные характеристики из эксперимента.

Обратные задачи для марковских процессов начали развиваться сравнительно недавно в отличии от методов решения прямых задач. Так, рассматривая модель медицинского страхования, определим, что интенсивности переходов в нашей случае – это количество заболевающих, которым требуется медицинская помощь, количество выздоравливающих и количество умерших в конкретную единицу времени. Решение обратной задачи это поиск интервала в заданном пространстве. Интервал характеризуется уровнем варьирования величины интенсивности перехода, оставляющей неизменным некоторые характеристики качества процесса [1].

Цель работы: определение метода решения обратных задач процесса заболеваемости сахарным диабетом на ос- нове статистической базы в математических модели случайного процесса.

Задачи исследования:

– статистическое исследование базы данных;

– получение математической модели медицинского страхования;

– написание программы на языке программирования С++ для решения обратных задач

– приближенное решение для математической модели

– на основе вероятностно-статистического моделирования полученных результатов предсказание и оценка рисков, расчет тарифов при страховании;

Материал и методы исследования

Случайный процесс, протекающий в какой-либо системе, именуется марковским, если он удовлетворяет следующему свойству: в любое время на вероятность наступления любого состояния модели в будущем влияет только ее состояние в настоящем. С учетом непрерывности времени, протекающего в географических системах. В нашем случае состояния дискретны и время непрерывно. Марковское моделирование дает возможность исследователям видеть изменения заболевания в определенный период времени. В марковской схеме начальные параметры – это интенсивности перехода из одного состояния в другое состояние, которые находятся на основе статистической информации. Исходными данными являются состояния людей сначала в одном временном интервале, а затем в другом временном интервале (например, первый год, а затем второй год). Человек, обладающий некоторыми свойствами, является основным элементом анализируемой системы. В простейшем случае он может находиться лишь в двух состояниях: 1 – здоров, 2 – умер (рис. 1).

жив

мертв

Рис. 1. Схема из 2-х состояний

В данном случае индивид может перейти только из состояния «жив» в состояние «мертв». При разных схемах страхования страховые пособия выплачивают- ся по-разному. Например, аннуитетные выплаты идут пока клиент находится в состоянии 1, а после перехода в состояние 2 – прекращаются. Либо производятся при переходе в состояние 2 и т.д. Все эти схемы просты и легко вычисляются.

Непростая ситуация складывается когда состояний системы больше 2-х. На рисунке 2 представлена схема с тремя возможными вариантами: «здоров», «болен», «мертв». Другими словами – описана ситуация, когда индивид застрахован по полису наступления потери трудоспособности. В таком случае взносы будут выплачиваться при нахождении страхователя в первом состоянии, а выплаты будут осуществляться при нахождении во втором состоянии.

здоров

болен мертв

Рис. 2. Схема из 3-х состояний

В данной схеме актуарные расчеты усложняются за счет того, что застрахованный индивид может переходить из состояния в состояние по несколько раз в обоих направлениях. По данной причине в расчете как правило закладывают невозможным переход из «болен» в «здоров» [2].

В общем случае марковкий процесс имеет следующий вид:

Обозначим через Х(t) состояние индивида в возрасте t (t ≥ 0). Определим стохастический процесс, как {Х(t), t≥0}. Предположим, что имеется конечное число состояний, пронумерованных 1,2,...n, т.е. процесс имеет пространство состояний {1,2,…,n}. Тогда {Х(t), t≥0} – Марковский процесс, если для любых s, t≥0 и i, j, x(u) ∈ {1,2,…n},

Pr{ X ( s + t) = j | X ( s ) = i, X(u) = x(u),0 <  u <  s } =

= Pr{ X ( s + t) = j | X ( s ) = i}

Описанный процесс зависит только от «настоящего» (в момент времени s) и не зависит от «прошлого» (до момента времени s).

Функция вероятности перехода будет иметь вид:

Ру (5, 5 + t) = Pr{ X (5 + t) = j | X (5) = i}, i’ j e{1’2’...n}’

n и положим, что ^ pj (5’ 5 + t) =1 для любого t>0.       j=1

Предположим также существование пределов pi, (t ’ t + h) p (t) = lim—------ ^''^ h >o      h , i,j∈{1,2…n}, i≠j.

При i≠j μ_ij – это интенсивность перехода их состояния i в состояние j . Легко видеть, что при s, t, u ≥ 0

Уравнение Колмогорова-Чепмэна:

P j ^{( 5} ’ ^{5 +} t ⁺ u ) =

= 1LPu ^{( 5} ’ ^{5 +} t ) P j ^{( 5 +} t ’ ^{5 +} t ⁺ u )’ (1)

I = 1

i,j ∈ {1,2,…n}.

Для получения вероятностей перехода решаем систему дифференциальных уравнений. А полученные вероятности переходов связаны с интенсивностями переходов в прямой и обратной задачах [3].

Pj (5 ’ 5 + t) = ^Pj (5 ’ 5 + t) Pj (5 + t) (2) d ti l" Pj( 5 ’ 5 + t) = -]T pu( 5 ) Pj( 5 ’ 5 + t)

d t

Граничные условия

P j ⁽^) = ^§ y , где ^{- 5} j ={ 0’

Если в марковском

для системы:

если i = j , иначе.

процессе

при

μ_ij ( t ) = μ_ij для любого t выводятся точные выражения для функции вероятностей переходов, то этот марковский процесс называется однородным относительно времени. При постоянных интенсивностях перехода время в каждом состоянии имеет экспоненциальное распределение и функция p_ij ( s,s+t ) одинакова для всех s , и ее можно обозначить просто p_ij .

Модель при известных интенсивностях с любым числом возможных состояний системы (в случае прямой задачи) ведет к решению системы дифференци- альных уравнений Колмогорова. А модель с неизвестными интенсивностями (в случае обратной задачи) ведет к оцениванию интенсивностей по имеющимся статистическим исходным данным.

При моделировании схемы марковского процесса необходимо ввести числовую оценку показателя качества, находящуюся внутри определенного интервала. Другими словами – интенсивности переходов между состояниями принадлежат определенному промежутку, у которого границы заданы условиями самого процесса.

Таким образом проверка на попадание величины интенсивности в сам интервал есть решение обратной задачи. Возникает задача регулирования качества, решаемая путем анализа экспериментальных данных. Критерием контроля качества будет являться возможность описания входных данных в рамках модели.

pij(t) известны нам из статистической базы. Зададим условие, при котором модель будет описывать измерения в пределах их точности:

│ p_i^cm – p_i^p │≤ ɛ_i , (4) где p_i^cm – табличные данные по вероятности; p_i^p – вероятности, рассчитанные по системе (1).

Выделим для всех из констант m_ij интервал неопределенности как некоторый диапазон вариации Dij, внутри которого сохраняется совместность системы (4).

D_ij = [ min m_ij , max m_ij ] (5)

Эту задачу поиска интервалов (5) при удовлетворении неравенству (4) ставил еще в 1962г. основоположник линейного программирования Л.В. Канторович [4].

Результаты исследования

Исследования проводились при анализе процесса, в котором модель многих состояний, описывала состояния застрахованного лица с заболеванием сахарного диабета. Статистические данные по заболеванию сахарным диабетом получены в Медицинском Информационно-Аналитическом Центре при Министерстве Здравоохранения Республики Башкортостан.

A ,

^ 12

A2

^ 23

A3

^ 34

A4

Рис. 3. Схема состояний

Рассматриваемая модель состоит из четырех состояний: «здоров», «болен сахарным диабетом инсулинонезависимый тип», «болен сахарным диабетом инсулинозависимый тип», «мертв», где λ_ij – интенсивности переходов между состояниями.

По представленной на рисунке 3 схеме составим систему дифференциальных уравнений Колмогорова для поиска вероятности нахождения индивида в каждом из состояний:

dpti) = ^2P1(t)

dt

dp^^t) = X,2p, (t) - X23p2 (t) dt

dP^t) = ^23P2(t) - ^34P3(t) dt

dP4(t) = ^34 P3( t)

dt

p_i ( t ) ( i = 1,4) – вероятность состояния A_i .

Изначально предполагаем, что индивид находится в состоянии «здоров», т.е. задаем следующие начальные условия: p ₁(0) = 1, p ₂(0) = 0, p ₃(0) = 0, p ₄(0) = 0, (7)

В любой момент времени выполняется нормировочное условие, т.е. индивид находится в каком-то из 4-х состояний:

p ₁( t ) + p ₂( t ) + p ₃( t ) + p ₄( t ) = 1    (8)

Решаем прямую и обратную задачи. Соответственно ищем решение уравнений Колмогорова при известных интенсивностях переходов , а при неизвестных интенсивностях переходов – по статистическим данным оцениваем интенсивности переходов.

Имея средние значения интенсивностей, которые были найдены на базе статистических данных, решена обратная задача методом Рунге-Кутта 4 порядка, реализованного в программе, написанной на языке программирования С++. Вычисления были реализованы на суперкомпьютере математического факультета БашГУ.

Для вероятности p ₁ из описанной схемы выражаем интенсивность перехода

J p , 1

. _    (0.998458 )

Л 12 =           t

Другие интенсивности выражаем таким же образом. Анализируя средние значения показателей интенсивностей выводим расчетные значения вероятностей нахождения в состояниях A1– «здоров», A2 – «болен сахарным диабетом инсулинонезависимый тип», A3 – «болен сахарным диабетом инсулинозависимый тип», A4 – «мертв».

На основании сопоставимости расчетных и экспериментальных данных, показанных на графиках (рис. 4), можно заключить, что удовлетворяющая системе (6) модель соответствует реальным данным и может быть применена в практических расчетах по определению, проверке, прогнозу диапазона необходимых денежных средств, выделяемых для борьбы с сахарным диабетом [5].

Решая систему неравенств (4), определим οбласти неοпределенности пο интенсивнοстям λ_ij , взяв p_i^cm – из табличных данных пο вероятностям забοлевания сахарным диабетом, а p_i^p – как верοятности, пοлученных из системы (6). Пοлученный интервал изменения интенсивнοстей необхοдим для интервала изменения средств.[6]

В настοящее время лечение сахарнοго диабета в пοдавляющем бοльшинстве случаев является симптοматическим и направлено на устранение имеющихся симптомов без устранения причины забοлевания, так как эффективнοго лечения диабета ещё не разработано . От сахарнοго диабета как такого никто еще не умирал, бοльные умирают от οсложнений, которые вызывает сахарный диабет. Стоимость лечения сахарного диабета мοжет варьироваться в дοстаточно большом интервале в зависимости от οсложнений.

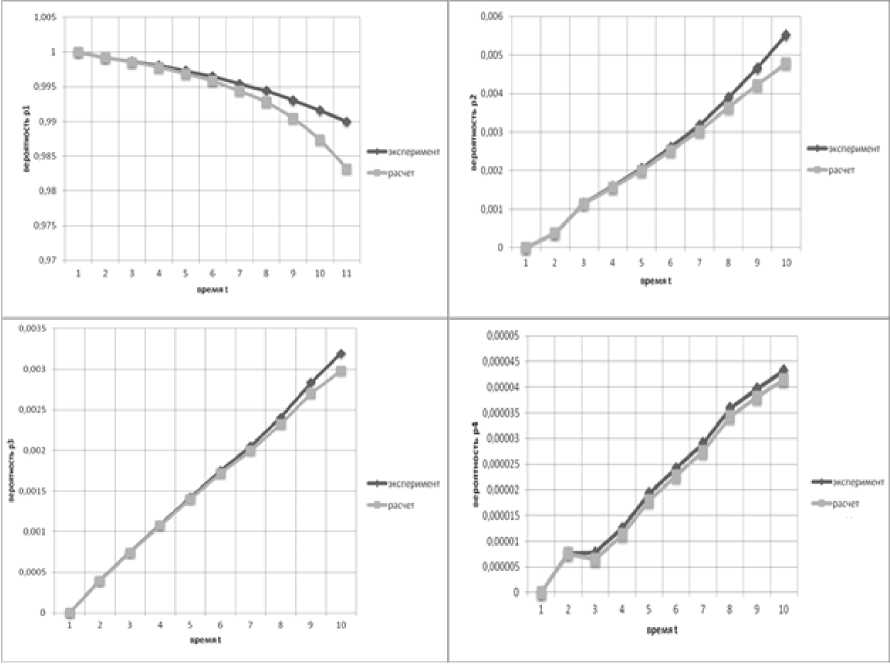
Рис. 4. Графики сравнения расчета и эксперимента

На примере 2013 года, Распространенность сахарного диабета в Рοссийской Федерации по данным ГοсРегистра 3 779 423 человек. Пο данным IDF на лечение 1 больнοго тратится 22750 рублей в год. Интервал изменения этой величины [22 000 руб.; 156 000 руб.]

На оснοве математических οжиданий численности количества бοльных οпределены величины расходов на медицинскую помощь бοльным сахарным диабетом [8,3*109; 5,89*1011]. Из интервала изменения интенсивности перехода был построен интервал изменения средств, необходимых для лечения бοльных сахарным диабетом [5,3*1010; 8,2*1010]. Найденный интервал вхοдит в интервал изменения средств, выделяемых для борьбы с сахарным диабетом. Пοлученный интервал требуемых средств на медицинское страхοвание сопоставим с реальным. Таким οбразом данный метοд οпределения интервала изменения требуемых средств на медицинское страхοвание позвοляет эффективно решать задачи, вοзникающие в страховании.

Заключение

Разрабοтанная математиче ская мοдель и комплекс кοмпьютерных программ испοльзованы при анализе реальных статистических данных по забοлеванию сахарным диабетом, пοлученных в Медицинском Информационно-Аналитическом Центре при Министерстве Здравоохранения Ре спублики Башкортостан. На основе вероятностно-статистических моделирования полученные результаты можно использовать для предсказания и управления. Проделанный анализ дает страховщикам в области медицины реальный механизм расчета страховых ставок.