Разработка метода экспертных оценок с применением алгоритма градиентного спуска

С 1950-х годов экспертное оценивание выделилось в отдельную научно-практическую дисциплину, в рамках которой были разработаны методы экспертных оценок, основанные на разных принципах действия. Результатом применения этих методов может выступать как определение наилучшего из предложенных вариантов, так и создание принципиально нового варианта.

Методы экспертных оценок востребованы при экспертизе научных исследований, принятии обоснованных организационных решений, выборе стратегий, аудите, оценке общественного мнения и др. Однако некоторые из них, такие, например, как метод Дельфи, метод голосования Борда, метод анализа иерархий, подвержены недостаткам, связанным с их организацией, и прежде всего – с субъективностью и узкой перспективой, вызванными ограниченным числом участников анализа. Это приводит к предвзятости конечных результатов [1]. Попытка ввести веса относительно мнений экспертов отчасти решает проблему субъективности. Однако может возникнуть проблема консенсуса, когда оценка сходимости мнений экспертов показывает низкий результат и приходится увеличивать временные затраты на проведение дополнительных раундов оценки. Кроме того, все традиционные методы полагаются в основном на эмпирические данные наблюдений для решения основных проблем, что лишь отчасти улучшает эти методы [2].

С учетом возможностей современных компьютеров и большого набора алгоритмов обработки данных может быть обоснованным и полезным создание метода экспертных оценок, стойкого к предвзятости экспертов. Оценка должна определять, насколько высоко оцененным разнородными группами экспертов окажется тот или иной вариант.

Создание такого метода является целью данной работы. Его формирование требует решения следующих программных задач: организация сбора мнений; выделение разнородных групп; взвешивание мнений; оценка предложенного варианта и присвоение ему одной из категорий: «качественный», «бесполезный», «необходимо больше оценок».

Проектирование алгоритма

Входные данные. Входными данными для такого метода являются мнения экспертов о полезности предложенных вариантов. Сбор мнений проводится посредством присуждения экспертом или пользователем одной из категорий предложенному варианту. Для упрощения в алгоритме представлены только три категории на выбор: «полезно или качественно» (соответствует численному значению 1), «бесполезно или некачественно» (соответствует числу 0) и «отсутствие оценки» (соответствует значению null), причем названия категорий и их количество могут быть изменены в соответствии с областью применения. Формой организации хранения данных выбрана матрица. Полученные численные значения, соответствующие выбранной категории, заносятся в матрицу оценок M , где каждая строка представляет собой оценки эксперта i , а каждый столбец – данные варианту j оценки, таким образом, элемент матрицы M_i,j – это оценка экспертом i варианта j .

Используемые факторы. Основная цель метода – предсказать оценку M_u,n , которая вычисляется по формуле

M u,n = V +i u ⁺ⁱn +f u f „ , (1) где V — глобальный средний рейтинг вариантов; i _u - смещение эксперта, его предвзятость; i_n – смещение варианта, универсальные характеристики, определяющие ее универсальную полезность; f_u,f_n – латентные векторы экспертов и вариантов соответственно.

Переменная V позволяет учесть общую склонность экспертов оценивать варианты как «полезные». Переменная выступает базовым уровнем оценки, к которому добавляется влияние других факторов.

Переменная i_u определяет уровень, насколько эксперт расположен позитивно или негативно оценивать варианты.

Переменная i_n определяет, насколько вариант оценивается как полезный в среднем, независимо от латентных факторов и индивидуальных предпочтений экспертов.

Переменная f_u отражает скрытые характеристики эксперта, которые влияют на его склонность оценивать определенные варианты. Эти факторы моделируют персональные предпочтения, которые невозможно явно измерить (например, предрасположенность к определённым типам данных или взглядов).

Переменная f_n отражает скрытые характеристики вариантов, которые влияют на их восприятие экспертами. Эти факторы моделируют свойства вариантов, которые могут быть важными для определённых групп экспертов (например, сложность изложения, специфичность аргументов).

Латентные векторы f_u и f_n , будучи использованными в скалярном произведении, позволяют определить взаимодействие между предпочтениями экспертов и характеристи-

Разработка метода экспертных оценок с применением алгоритма градиентного спуска ками вариантов [3]. Высокое значение fufn увеличивает вероятность положительной оценки, предсказанной алгоритмом, отражая совместимость между предпочтениями эксперта и характеристиками варианта.

Выбор именно таких переменных способствует достижению целевых качеств метода. Во-первых, такая структура обеспечивает выявление вариантов, которые могут быть расценены широким набором разнородных экспертов как полезные или качественные, что исключает возможность целенаправленного искажения оценки варианта консолидированной группой экспертов. Во-вторых, добавление смещений к модели позволяет учесть систематические отклонения, что уменьшает влияние случайных отклонений [4]. Кроме того, применение латентных векторов позволяет моделировать различия в восприятии вариантов разнородными экспертами, избегая применения простой категоризации и кластерного анализа [5].

Выбор алгоритмов для обучения модели. В качестве технологии, используемой для предсказания конкретной оценки, выбрана модель, основанная на матричной факторизации, уже отраженная в формуле (1) в виде скалярного произведения двух латентных векторов с наличием дополнительных переменных. Такая модель позволяет спрогнозировать оценку на основе исторических данных (то есть предыдущих оценок экспертов), что позволяет не дожидаться оценки варианта от всех экспертов.

Для обучения модели используется алгоритм градиентного спуска . Сначала переменные модели инициируются случайными значениями, что создает начальную точку для градиентного спуска, а затем вычисляется функция потерь, то есть разница между реальными оценками в матрице и предсказанием модели [6]. С помощью градиентного спуска пересчитываются новые значения переменных так, чтобы смоделированная оценка была ближе к настоящей оценке. Итогом обучения модели становится набор числовых значений всех переменных модели, среди которых решающей переменной будет i _n , отражающая универсальную полезность либо качественность варианта. Таким образом, отбор по полезности позволяет выявить варианты, получающие межгрупповое одобрение, и отсеять варианты, вызывающие одобрение одной группы за счет отторжения со стороны другой группы.

Однако в ходе обучения модели может возникнуть проблема переобучения, когда параметры модели становятся слишком большими, например, когда вариант оценен небольшим числом экспертов [7]. Для снижения риска возникновения этой проблемы в функцию потерь необходимо внедрить механизм регуляризации, который добавляет штраф к значению ошибки [8]. Кроме того, необходимо ввести два коэффициента регуляризации. Первый из них будет иметь значение большее, чем второй. Первый коэффициент будет применен для вычисления ошибки переменных i_u и i_n , второй – для вычисления ошибки латентных векторов f_u и f_n . Применение большего коэффициента регуляции к смещениям вызвано тем, что эти параметры линейны и сильно влияют на результат. Латентные векторы являются более гибкими параметрами, поэтому они могут потерять свою значимость при большом значении регуляционного коэффициента [9]. Сама функция потерь будет основываться на методе наименьших квадратов, что обеспечит отображение ошибки в позитивных значениях и позволит большим ошибкам штрафоваться сильнее [10]. Функцию потерь с учетом всех введенных ограничений можно представить как

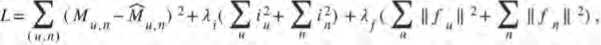
где M u, n - реальная оценка варианта n экспертом u ; M _u , n - предсказанная моделью оценка варианта n экспертом u ; i_u и i_n – смещения эксперта и варианта соответственно; A i , A f - коэффициенты регуляризации для смещений и латентных векторов соответственно, причем A i < A f .

Окончание работы алгоритма моделирования оценки должно прийтись на выполнение одного из условий: либо значение функции потерь L перестает снижаться, либо достигается заданное максимальное количество итераций.

После того как моделью было подобрано значение полезности варианта i_n , соответствующий вариант n необходимо категорировать и присвоить ему одну из трех категорий: «качественный», «бесполезный» или «необходимо больше оценок» [11]. Очевидно, что при значении i_n > 0 вариант будет скорее полезным, а при i_n< 0 – бесполезным, однако необходимо определить пороги значений i_n , при которых вариант будет с большей вероятностью соответствовать одной из категорий. Решить эту проблему можно с помощью анализа распределения значений i _n после обучения модели [12].

Полученный алгоритм работы метода отображен на Рисунке 1.

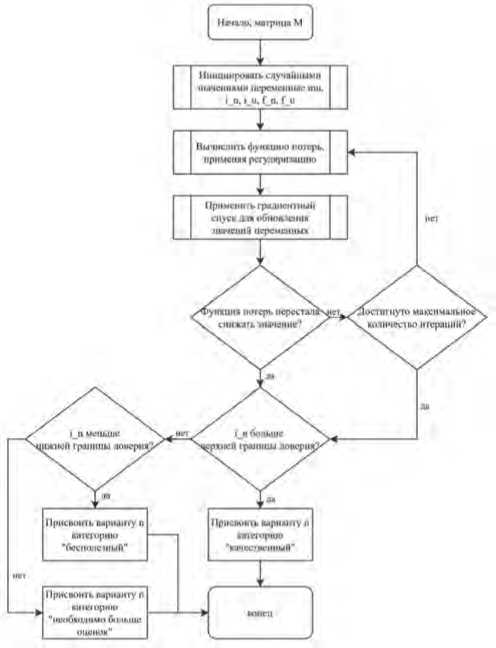
Рисунок 1. Блок-схема алгоритма

Источник: здесь и далее рисунки выполнены авторами

Разработка метода экспертных оценок с применением алгоритма градиентного спуска

Для обновления данных о варианте данный алгоритм нужно периодически запускать заново с новыми данными для пересчета показателей каждого варианта.

Проверка разработанного метода

Особенности проведения эксперимента. Для проведения экспериментов и изучения полученных данных была реализована программа на языке программирования Python, представляющая метод и модель в упрощенном виде за счет нескольких особенностей: генерируется матрица оценок со случайными значениями, причем эксперты разделены на две группы, которые оценивают одну группу вариантов положительно, а другую – отрицательно; градиентный спуск реализован базово: изменяется значение показания на небольшую разницу, и если при нем уменьшается ошибка, то оно сохраняется, а если ошибка увеличивается – разница возвращается обратно.

Выделение разнородных групп экспертов и вариантов. Цель эксперимента заключается в проверке способности алгоритма правильно различать предлагаемые варианты разного качества на основе латентных параметров. Кроме того, эксперимент поможет оценить, как поляризация во мнениях экспертов и случайные начальные значения влияют на финальное распределение значений полезности. Для достижения этой цели в коде сначала выполняется деление экспертов на две группы: если эксперты принадлежат одной группе (вычисляется по выполнению условия i%2 =v%2 , где i – индекс эксперта, ν – индекс варианта), то оценка экспертом i варианта ν будет равна 1, в другом случае – минус 1. Затем варианты делятся на четыре группы: «хорошие», «поляризующие», «нейтральные» и «плохие». Для первой четверти столбцов матрицы оценка увеличивается на 1 при условии, что оценка уже стояла. Для второй четверти столбцов оценка увеличивается в три раза и на единицу при условии, что оценка уже стояла. Для третьей четверти столбцов изменения не применяются; для четвертой четверти столбцов оценка уменьшается на 1 при условии, что оценка уже стояла. После этого производится запуск алгоритма. В результате его работы замеряются средние значения качества варианта i _n для каждой группы вариантов.

Проверка результатов. В результате проведения эксперимента с условиями, что коэффициент регуляризации для латентных векторов составляет 0,05, коэффициент регуляризации для остальных переменных 0,15, число экспертов и вариантов составляет 16, число оценок каждого эксперта – 4, были получены результаты, представленные на Рисунке 2.

Результаты эксперимента показывают, что модель устойчива и корректно определяет значение полезности у соответствующих вариантов: in1>in2>in3>in4 [13]. Кроме того, по этим показателям можно настраивать доверительные границы для определения категорий каждого из вариантов. Например, при значении полезности большем, чем 0,4, вариант может быть категорирован как «качественный»; при значении меньше минус 0,09 вариант может быть категорирован как «бесполезный». Кроме того, проведенный эксперимент показывает, что «хорошие» варианты имеют стабильно высокие оценки полезности, «поляризующие» – умеренные значения, «нейтральные» – значение полезности ближе к нулю, а «плохие» – стабильно отрицательные показатели полезности, что показывает устойчивость модели к поляризации мнений экспертов и ее способность корректно разделять варианты на категории, несмотря на случайные начальные условия. Результаты подтверждают, что модель адекватно отражает различия в качестве вариантов и мо- жет эффективно учитывать как объективные характеристики, так и субъективные предпочтения разных групп экспертов.

Средние значения качества варианта:

Группа 1 (хорошие): 0.42886697257195794

группа 2 (хорошие, но поляризующие): 0.17060670210081832

Группа 3 (нейтральные): 0.12215714290055185

Группа 4 (плохие): -0.140739208456402

Рисунок 2. Полученные в ходе эксперимента средние значения оценки качества вариантов по группам

Сравнение разработанного метода с традиционными методами экспертных оценок

Для более полного анализа эффективности разработанного метода экспертных оценок проведено его сравнение с традиционными и современными подходами: методом Дельфи, методом аналитической иерархии (AHP), методом голосования Борда и машинными методами (кластеризация). Выбор данных методов обусловлен их популярностью и применимостью в различных областях. Метод Дельфи широко применяется в стратегическом планировании и прогнозировании, ориентирован на консенсус. Метод аналитической иерархии (AHP) представляет собой гибридный подход, сочетающий парные сравнения и весовые методы, что делает его полезным для многокритериальных задач. Метод голосования Борда выделяется своей простотой и эффективностью при ранжировании вариантов, особенно в условиях группового принятия решений. Машинные методы (кластеризация) добавлены в сравнительный анализ как современные подходы, применимые к большим данным и автоматической обработке оценок [14].

Сравнение проводится по ключевым характеристикам: точность, объективность, учет поляризации, гибкость, сложность реализации, устойчивость и области применения. Результаты представлены в Таблице.

Таблица

Сравнительный анализ разработанного метода и традиционных методов экспертных оценок

Характеристика	Разработанный метод	Метод Дельфи	Метод AHP	Метод голосования Борда	Машинные методы
Точность и объективность	Высокая за счет минимизации ошибки	Средняя, возможна субъективность	Высокая при четких критериях	Средняя, зависит от голосующих	Высокая, зависит от данных
Учет поляризации мнений	Учитывает разногласия и скрытые факторы	Низкая, стремление к консенсусу	Не учитывается, важны критерии	Не учитывается, все голоса равны	Частично, через кластеризацию
Гибкость настройки	Высокая, можно настраивать параметры и пороги	Низкая, фиксированный процесс	Средняя, через вес критериев	Низкая, фиксированное ранжирование	Высокая, настраиваются алгоритмы
Сложность реализации	Низкая, требует первоначальной реализации и исторических данных	Средняя, требует координации экспертов	Средняя, требует расчета весов	Средняя, требует подсчета голосов	Высокая, требует подготовки данных при каждом новом применении

Разработка метода экспертных оценок с применением алгоритма градиентного спуска

Продолжение таблицы

Устойчивость	Высокая даже при случайных начальных данных	Средняя, зависит от экспертов	Средняя, зависит от критериев	Низкая, результаты зависят от голосов	Высокая из-за устойчивости модели
Области применения	Сложные задачи с большими данными	Стратегическое планирование, прогноз	Задачи с множеством критериев	Принятие решений в управлении	Автоматическая обработка больших данных

Источник: таблица выполнена авторами.

В результате сравнительного анализа можно утверждать, что разработанный метод экспертных оценок является более точным, гибким и устойчивым решением, особенно в условиях поляризации мнений и необходимости работы с большими данными. Однако он требует значительных вычислительных ресурсов и накопленных исторических данных, что делает его менее подходящим для задач, где важны простота и скорость реализации. Для небольших и структурированных задач традиционные методы (Дельфи, AHP, Борда) остаются конкурентоспособными ¹ .

Выводы

В результате исследования предложен и реализован новый метод экспертных оценок, основанный на применении алгоритма градиентного спуска и матричной факторизации. Метод демонстрирует существенную новизну благодаря способности учитывать поляризацию мнений экспертов через использование латентных факторов, которые отражают скрытые предпочтения различных групп экспертов и характеристики оцениваемых вариантов, что позволяет выделять те варианты, которые получают межгрупповое одобрение, и исключать влияние предвзятости отдельных групп.

Одним из ключевых качеств разработанного метода является высокая точность и объективность, которые достигаются за счёт минимизации функции потерь при обучении используемой модели, что позволяет учесть как общие тенденции, так и индивидуальные особенности каждого эксперта. В отличие от традиционных методов, таких как метод Дельфи, новый подход не требует достижения полного консенсуса между экспертами. Вместо этого он эффективно обрабатывает данные в условиях разногласий и поляризации, что особенно важно при анализе сложных систем с разнородными участниками. За счет использования исторических данных метод масштабируется сам по себе, что расширяет возможности и удобство его применения.

Проведенный эксперимент подтвердил устойчивость метода к групповым сговорам и случайным начальным условиям и позволил сделать вывод, что модель способна корректно разделять варианты на категории и учитывать разногласия между группами экспертов.

Разработанный метод также обладает высокой устойчивостью благодаря использованию регуляризации, что снижает риск переобучения модели. Таким образом, модель адекватно отражает как объективные характеристики вариантов, так и субъективные предпочтения экспертов, что делает ее универсальным инструментом для анализа данных в условиях поляризации мнений.