Разработка методики бездатчикого определения углового положения ротора синхронного двигателя на основании дополнительного сигнала высокой частоты

Развитие электропривода приводит к необходимости решения проблем, связанных с его массогабаритными параметрами [1–3]. Одним из возможных способов, позволяющих добиться положительного результата в этом направлении, является отказ от использования механических датчиков [4–8]. С другой стороны, обойтись без величины углового положения невозможно, поэтому предлагается определять её с помощью косвенных показателей, которыми являются величины напряжения или тока электропривода.

Кроме отмеченного уменьшения габаритных показателей бездатчиковые способы определения углового положения также позволят добиться таких преимуществ, как:

• -    уменьшение стоимости системы электропривода;

• -    увеличение надежности электропривода.

Согласно [9] векторное управление двигателем переменного тока приводит к необходимости определения угловой величины на трёх этапах:

• -    начальное положение ротора;

• -    величина угловой скорости (положения) в диапазоне скорости двигателя, не превышающем 10 % от номинального значения;

• -    номинальный режим работы [10].

В работах [11–18] угловое положение ротора определяется на основе оценивающих моделей. Внедрение подобных решений обусловлено для электроприводов с небольшим диапазоном регулирования скорости (не более 1 : 100) [11–16], либо при невозможности установки датчика на двигатель по причине нехватки места [17, 18].

Недостатки оценивающих моделей заключаются в следующем:

• -    разработанные наблюдатели состояния (Калмана, Люенбергера и др.) не позволяют отслеживать угловое положение ротора во всем диапазоне частот;

• -    в диапазоне низких скоростей величина погрешности углового положения может достигать значительной величины, так как необходимо учитывать поправку на «мертвое время» и время задержки переключения ключей инвертора;

• -    вариации активного сопротивления, взаимоиндукции двигателя переменного тока при его работе под воздействием температуры вносят погрешность в расчеты наблюдателей состояния по определению углового положения ротора.

В работе [19] авторами данной статьи была предложена упрощенная классификация всех без-датчиковых методов определения углового положения. Предложено выделить две группы определения углового положения ротора без использования механического датчика:

• -    на основе противоЭДС;

• -    на основе измерения индуктивности фазы статора.

В работе [20] рассмотрены преимущества, недостатки и ограничения каждого из методов, относящихся к двум выделенным категориям. Основной недостаток рассмотренных бездатчиковых систем заключается в невозможности определения углового положения при нулевой и низкой, не превышающей 10 % от номинальной, скорости.

Целью данной статьи является теоретическое обоснование методики определения углового по- ложения ротора синхронного двигателя с помощью подачи сигнала высокой частоты в обмотку возбуждения.

Для достижения поставленной цели необходимо решить следующие задачи:

• -    проанализировать взаимосвязь углового положения ротора с величинами ЭДС, наводимых на обмотке статора;

• -    разработать структурную схему определения углового положения ротора;

• -    проанализировать полученные результаты величины углового положения ротора в области нулевой и низкой скорости.

Теоретическое обоснование метода определения углового положения ротора синхронного двигателя с помощью инжекции высокочастотного сигнала

Функциональная схема электропривода с без-датчиковым определением углового положения ротора на основе подачи сигнала высокой частоты в обмотку возбуждения представлена на рис. 1.

Сигнал высокой частоты (в работе [19] доказана величина в 1000 Гц) подается в обмотку возбуждения синхронного двигателя. В обмотках статора наводятся ЭДС. Выделение высокочастотной составляющей сигнала напряжения (U af , U bf , U cf ) происходит с помощью полосно-пропускающих фильтров (ППФ). В блоке определения углового положения ротора осуществляется процесс сравнения выделенных сигналов напряжения и сравнение их с переменной составляющей сигнала возбуждения (U_f). Вычисленный сигнал поступает в блок преобразователя частоты для реализации векторного управления синхронным двигателем.

В работе [17] предлагается схема определения углового положения ротора, позволяющая определять искомую величину с точностью в 30°.

Чаще всего подобной точности недостаточно для того, чтобы реализовать векторное управления двигателем переменного тока. Поэтому актуальным является анализ зависимости углового положения от величин напряжений на статоре 9 = f(Ua, Ub, Uc).

Процесс вывода данного выражения начнём с записи уравнений Парка – Горева для синхронной машины [21, 22]:

• "57+ ®Tq + rid = -ud ;

^Td - ddT - riq = Uq;

^ + rrir = Er;(3)

^ + ^1^ = 0, i = 0^nd;(4)

^^ + rrqkirqk = 0, k = 0 - nq;(5)

Td = Ldid + Madir + Mad ЕГД irdt;(6)

Tq = Lqiq + MaqZk'1irqk;(7)

Tr = Lrir +1 Madid + Mad Z"-i irdt;(8)

Trd1 = Lrd1ird1+| Madid + Madir + +MadZ"=iirdii, i = 0-nd;(9)

1*1

Trqk = Lrqkirqk + 2 Maqiaq + Maq ^j-i irqjk, j*k k=0-nq;(10)

ldi|=MT-|(Tdiq- Tqid),(11)

где r, rr, rdi, rdk – активное сопротивление обмотки статора, обмотки возбуждения i-го продольного и k-го поперечного демпферных контуров;

Ld, Lq – индуктивности обмотки статора;

Lr, Lrdi, Lrdk – индуктивности обмотки возбуж- дения;

Mad – взаимная индуктивность в оси d;

M aq – взаимная индуктивность в оси q;

E r – напряжение возбуждения;

Л = w/p - угловая скорость вращения ротора;

P – число пар полюсов машины.

В качестве начального условия будем рассматривать случай, при котором статор синхронного двигателя не подключен к трехфазной сети переменного тока. Следовательно, в обмотках статора не будет фазных токов. При подобных рассуждениях можно значительно упростить уравнения

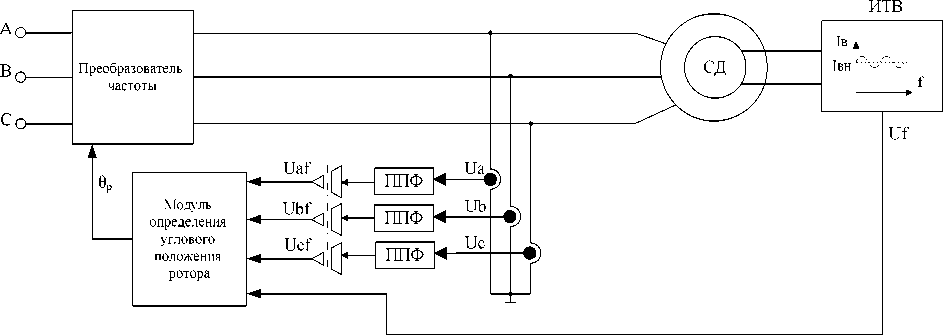
Рис. 1. Функциональная схема электропривода с бездатчиковым определением углового положения ротора

(1)–(11). Определить величину проекции напряже-

приведения. На основании этого получено выра-

ния на ось q:

U q = R_Si q+^ ф_ч- ® R ® d .               (12)

На основании начальных условий

U q = 0.                                    (13)

Из формулы преобразования координат из-

жение

sin9cos-+cos9sin-1

3           3

------------ - — — .

sin9

вестно, что

U q = | (u a COS(9) + U_b COS (9 — j) +

+ U c COs(9 + 7)),                      (14)

где u a , u b , u c – мгновенные значения фазных на-

Разделим поочередно левую часть уравнения (17) на sinθ. В результате получим

0,5 + 0,866ctg9 = — к .                    (18)

Выразим из выражения (18) величину ctg9,

получим ctg9 =

4~°,⁵ 0,866 .

пряжений.

Подставив выражение (14) в (13), учитывая

Окончательный результат приведем к виду

симметричность трехфазной системы, а формулы сложения косинусов, получим yUa Sin (9 +1) + yUb sin(9) = 0.

Запишем выражение (15) в виде:

sin(9+n) = _Ub sin (9)          ua.

так же

„        . (-0,86б\

^{9    JlCt;}l- ■ ।

+ 180n,

где n – величина, равная 0, 1 или 2 в зависимости

Отношение U a /U b примем равным k. Выражение (16) может быть упрощено согласно формуле

от положения ротора.

Коэффициент n необходимо использовать по причине наличия в формуле (20) функции arctg.

На основании формулы (20) была проведена модернизация схемы, представленной в [17]. Улуч-

шенная структурная схема модуля определения углового положения ротора представлена на рис. 2.

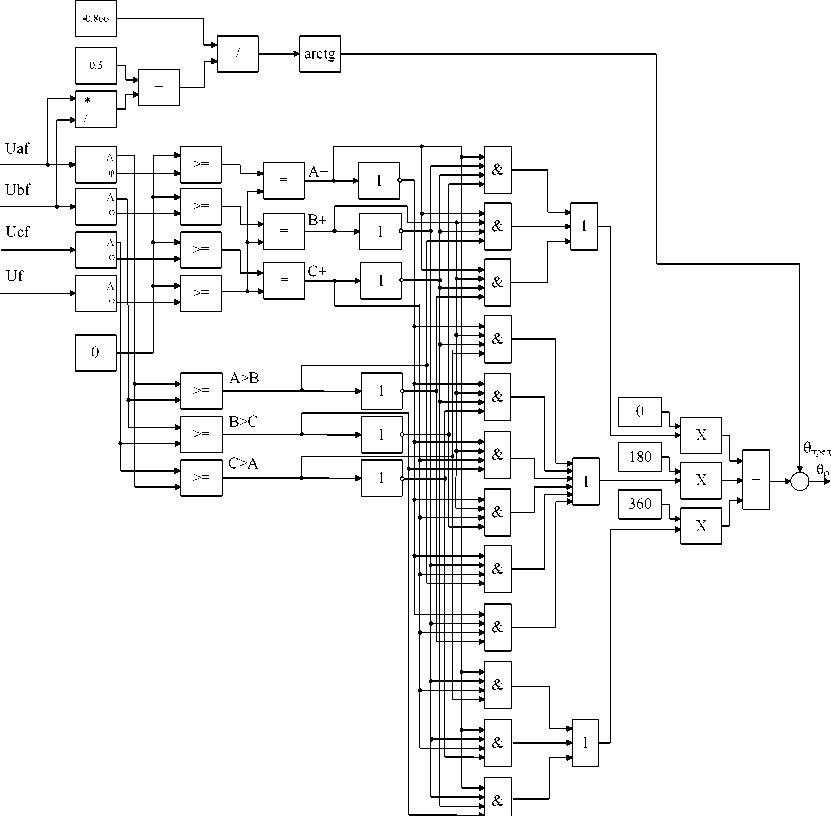
Рис. 2. Структурная схема модуля определения углового положения ротора

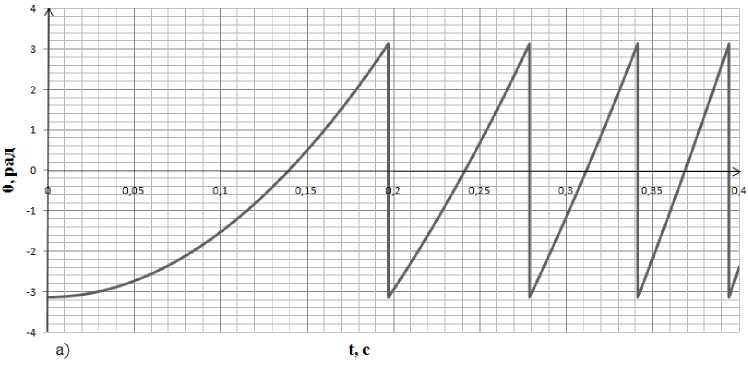
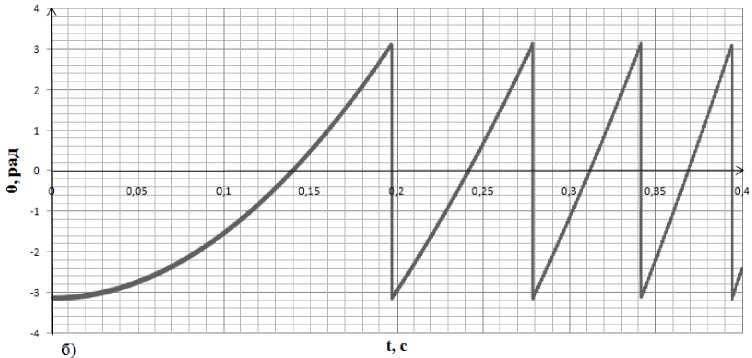
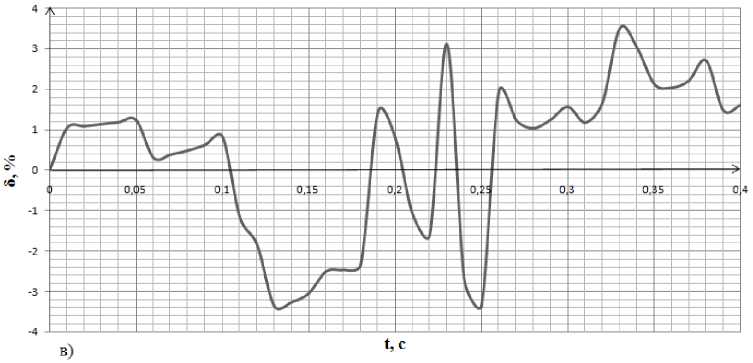
Рис. 3. Сравнение углового положения ротора: а – график изменения углового положения ротора в бездатчиковой системе; б – график изменения углового положения ротора в электроприводе с механическим датчиком; в – график относительной погрешности

Проверка работоспособности электропривода с бездатчиковым определением углового положения ротора была осуществлена за счет сравнения угловой величины, полученной в бездатчиковой модели (рис. 3а), и угловой величины в аналогичном электроприводе с механическим датчиком (рис. 3б). Обе модели разработаны на основе функциональной схемы (см. рис. 1) в программе MATLAB Simulink.

Вывод

В результате проведенного анализа бездатчи-ковых методов определения углового положения ротора двигателей переменного тока выявлено, что они обладают одним общим недостатком, который связан с трудностью определения угловой величины при низких и нулевых скоростях. В статье дано теоретическое обоснование метода определения угловой величины на основе подачи сигнала высокой частоты в обмотку возбуждения ротора синхронного двигателя. Осуществлён вывод выражения, обуславливающего зависимость углового положения ротора от наводимых в статоре высокочастотных составляющих ЭДС. На основе предложенного выражения разработана модель электропривода, анализ которой показал, что величина погрешности предложенного метода при сопоставлении с параметром углового положения, измеренного с помощью механического датчика, не превышает 3,8 %.