Разработка методики моделирования зубчатых передач на основе метода математического моделирования векторных замкнутых контуров

что для плоских моделей, таких модулей всего 4, а для пространственных 20 [1].

Построенная на основе модулей основная векторная модель - позволяет получить решение определенных функций, с известными для каждого момента времени аргументами модели и связями между отдельными векторами и контурами.

Инвариантность метода математического моделирования векторных контуров позволяет решать, кроме задач анализа и синтеза механизмов, как различные сопутствующие задачи, так и задачи, выходящие за рамки моделирования только рычажных механизмов, например в различных задачах реального проектирования механизмов летательных аппаратов, машин объемного расширения [4].

Использование модульных векторных моделей позволяет оперативно решать, как задачи реального проектирования, так и задачи оперативного контроля, например шестеренных насосов. Шестеренные насосы обладают простотой конструкции, малой трудоемкостью изготовления, сравнительно небольшими габаритами и массой, возможностью непосредственного соединения с быстроходными двигателями. В тоже время к недостаткам шестеренных качающих узлов следует отнести чувствительность к механическим примесям в перекачивающей жидкости; рост зазоров в процессе эксплуатации, вызывающий увеличение утечек; неравномерность подачи жидкости и высокий уровень акустического шума. Для снижения интенсивности колебательных и кавитационных процессов необходима разработка методов оперативного и адекватного учета кинематической подачи жидкости при измененной геометрии профиля зубьев насоса (рис. 2).

В принципе данная задача решается построением математической модели, описывающей эвольвенту поверхности зуба, например цепочкой векторных контуров вдоль профиля зуба, но подобная модель обладает жесткой структурой – количеством векторов, жестко заданными параметрами векторов, что создает достаточно большие неудобства в перенастройке данной векторной модели ввиду необходимости вводить(-или изменять) большое количество векторов для обеспечения достаточной точности построения профиля эвольвенты. Поэтому для построения такого сложных варианта контурных систем, был применен новый подход моделирования векторных систем.

Основной примененного данного подхода является ввод новых понятий – “промежуточных аргументов” и “векторной контурной модели одной точки профиля (кривой)”.

Разбиваем задачу на следующие 2 подзадачи:

• 1.    Описание поверхностей зуба 1 и 2.

• 2.    Описание высоты зуба А в конкретном сечении.

Попробуем решить поставленные подзадачи с помощью метода моделирования векторных замкнутых моделей.

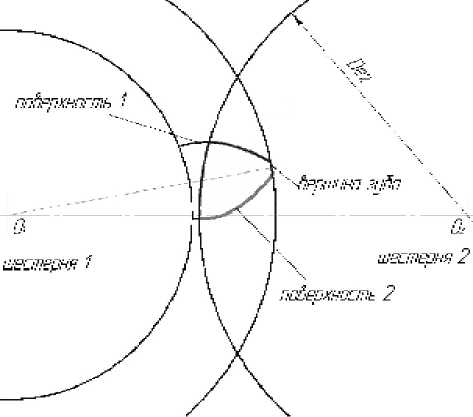
Рис. 2. Описываемые поверхности зуба

1. Поверхность зуба строится по свойству эвольвенты (рис 3).

Заменяем радиус О₁ А₁^/ вектором 1, касательную А₁^/ B₁^/ вектором 2. Для замыкания векторного контура используем вектора 3 и 4. Причем вектор 3 параллелен оси ординат, а вектор 4 – оси абсцисс (рис. 4).

В результате получили векторный контур, описывающий эвольвенту поверхности 1 зуба шестерни 1.

Длина вектора 1 равна радиусу основной окружности r ₀ .

Угол вектора 1 изменяется в определенных числовых пределах.

Длина вектора 2 изменяется в определенных числовых пределах.

Угол вектора 2 связан с углом вектора 1 зависимостью ф 2 = ф 1 + Аф , где Аф - шаг угла поворота.

Длины векторов 3 и 4 неизвестны.

Полученный векторный контур описывается с помощью модуля Пл2 ( p 3 ,p₄ ) [1].

Аналогично описывается поверхность 2 зуба шестерни 1 (рис. 5).

При анализе рисунков 4 и 5 видно, что подзадача 2 решается сложением длин векторов 3 и 7, таким образом в конкретном случае мы получаем толщину зуба.

Объединим полученные две модели в модель 3 (рис. 6).

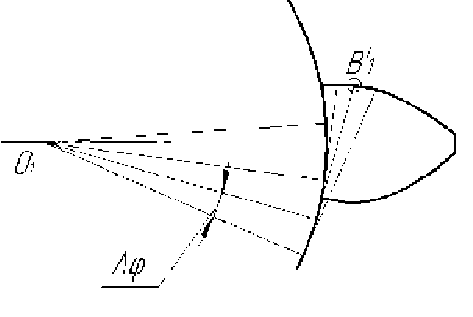
Рис. 3. Построение поверхности зуба

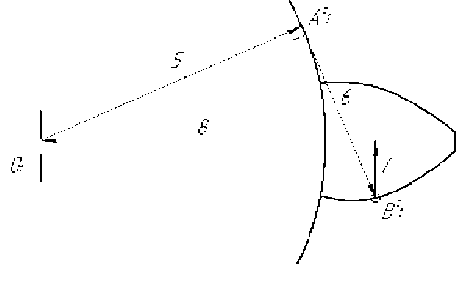
Рис. 5. Поверхность 2 зуба шестерни 1

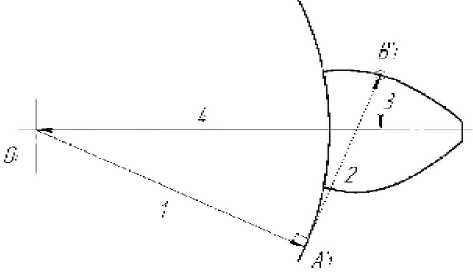
Рис. 4. Векторный контур

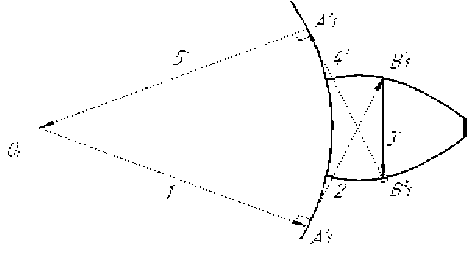
Рис. 6. Объединенная векторная модель

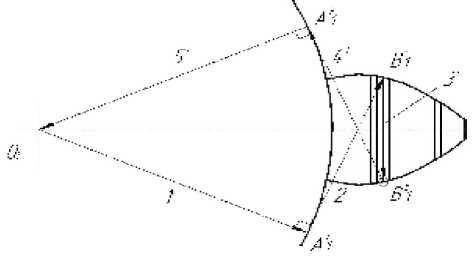
Рис. 7. Траектория поверхностей зуба

Отложим вектора 1 и 2 без изменений, т.е. так, как они были в первом векторном контуре (рис. 4). Вектора 3 и 7 объединим и получим вектор 3/. Вектора 5 и 6 отложим как прямые, без указания их направления. Дадим им направления так, чтобы замкнуть полученный контур.

В результате обе подзадачи решаем одной полученной моделью (векторным контуром 1-2-3/-4/-5/).

Для определения координат точек Б ^ и Б ^ используем вспомогательные векторные модели, сходные с моделями 1 и 2. Изменение углов наклона векторов 1 и 5 и длин векторов 2 и 4 позволяет получить траекторию поверхностей зуба (рис. 7).

Построенная модель описывает поверхность отдельного зуба шестерни в один и тот же момент времени, параметры углы наклона векторов 1 и 5 и длины векторов 2 и 4, являются промежуточными одномоментными по времени аргументами. Введение этих же параметров в основные аргументы модели позволяет получить поворот зуба и описать положение зуба в различные моменты времени. На рис.8 приведен модель зуба, с каверной поверхности, некоторые векторы модели не отображены.

Простота данной модели с одной стороны и возможность увеличивать или уменьшать шаг изменения промежуточных и основных аргументов модели с другой, позволяют оперативно добиваться нужной точности вычислений при описании поверхности зуба шестерни и его движении.

Рис. 8. Модель зуба с каверной поверхности