Разработка методики построения физико-математических моделей термодинамических процессов многофазных потоков наружных сетей теплоснабжения

Развитие и модернизация старых объектов внутри муниципальных образований, а также строительство новых формируют потребности создании систем теплоснабжения иного уровня и качества относительно проектируемых и создаваемых в настоящее время.

Современные системы центрального теплоснабжения как модернизированные, так и создаваемые вновь, не всегда обеспечивают необходимое качественное теплоснабжение для конечных потребителей и зачастую не поддерживают высокий уровень надежности.

Развитие цифровых технологий и активное внедрение технологии «больших данных» позволяют научному сообществу активно искать качественные и высокотехнологичные прорывные решения для развития данной отрасли.

Для более глубокого понимания и прогнозирования происходящего внутри трубопровода системы централизованного теплоснабжения необходимо наличие модели, учитывающей большинство параметров такой системы. При этом модель должна обладать необходимыми физическими свойствами потока.

Термодинамические процессы многофазного потока в «разрезе» при создании такой физикоматематической модели рассматривают прежде всего перемещения рабочего тела, обладающего различными термодинамическими параметрами и формами течения в одну единицу времени внутри трубопровода.

Актуальность. Разработка подобной физикоматематической модели и методика ее создания являются одной из актуальнейших проблем для современного теплоснабжения. Ключевые новейшие элементы для создания, проектирования и реализации систем централизованного теплоснабжения 4-го поколения [1] заключаются в использовании цифровых технологий, обработке боль-

ших данных и прогнозировании поведения рабочего тела в частности и самой системы теплоснабжения в целом. Чем сложнее для обработки компьютером будет физико-математическая модель, тем больше потребуется его ресурсов производительности и тем медленнее будет формироваться итоговый результат (отчет, прогноз, анализ и т. д.) [1–10].

Научная новизна. Для формирования концепции нового поколения измерительно-вычислительных комплексов диагностирования сетей теплоснабжения нужна упрощенная для вычисления, но при этом наиболее точная физико-математическая модель термодинамических процессов многофазных потоков наружных сетей теплоснабжения. В данной работе рассмотрены особенности моделирования однотрубных систем теплоснабжения с рабочим телом в виде технической воды, с возможностью возникновения многофазных потоков. Представлено нововведение в существующие TVD-схемы и WENO-схемы в виде описания представления математического движения многофазного потока с учетом непрерывности производных.

Материалы и методы исследований

В настоящее время существует множество типов многофазных потоков [11]. Разработку физико-математической модели необходимо начинать с поиска общего для всех подобных потоков параметра, а именно – давления. Ввиду того, что рассматривается многофазный поток и его термодинамические процессы внутри системы теплоснабжения, необходимо учитывать то, что давление внутри системы строго регламентировано технической документацией. Это дает возможность использования неявного, экономичного алгоритма численного интегрирования системы уравнения для описания многофазного потока, отображенного в исследовании [12]. Необходимо отметить, что

физико-математическая модель разрабатывается под особенности системы теплоснабжения города Норильска, в котором техническая вода для горячего водоснабжения не проходит процедуру полного цикла очист-

ки, а значит, при рабочем режиме существует многофазность рабочего тела.

Использование подобного алгоритма будет эффективно, поскольку он описывает пространство некоей объемной доли жидкости, элементы которой находятся в различных состояниях:

d (А ^akPk^uk )    d (А ^akPk^uk+ А OkP )

dt               dx

-

n- (А Ok ⁾ =0,

где d^ – объемная доля жидкости, %; Pk – плотность жидкости, кг/м³; ^uk – скорость жидкости, м/с; к – общее количество жидкости; P – общее давление в трубопроводе, Па; А – площадь сечения трубопровода, м²;

t – время, с; X – координата вдоль образующего канала, м.

Подобная формула математически корректно описывает вышеуказанное определение многофазного потока [13]. Однако ее необходимо дополнить математическим описанием термодинамических процессов, происходящих в момент его перемещения внутри трубопровода.

Результаты исследования и выводы

Термодинамические процессы можно выразить математически как непрерывные процессы, представления о которых можно получить с помощью осреднения параметров фаз рассматриваемого потока [14], поскольку свойство непрерывности свидетельствует, что малые изменения аргумента приводят к малым изменениям значения функции. Однако необходимо отметить, что рассматриваемый поток прежде всего гетерогенен, а значит, обладает явлением межфазного взаимодействия. Подобное взаимодействие должно быть учтено добавлением в уравнение соответствующих дифференциальных членов.

Описание межфазного взаимодействия математическим языком является классической проблемой при подобного рода моделировании. Решение данной проблемы путем использования принципа Гамильтона рассмотрено в научных работах [15–17]. В свою очередь использование этого принципа привносит в поставленную задачу ряд более мелких проблем, таких как негиперболичность системы уравнений и наличие уравнений, которые невозможно представить в дивергентной форме.

В связи с этим к формируемой физико-математической модели с целью ее усовершенствования необходимо предъявить ряд требований.

• 1.    Гиперболичность системы уравнений, то есть с имеющимися начальными данными эта система уравнений должна быть однозначно разрешима в рассматриваемом пространстве.

• 2.    Уравнение должно быть записано в дивергентной форме, то есть уравнение с дифференциальным оператором, которое способно отображать векторное поле на скалярное, определимое для каждой точки

• 3.    Согласованность полученной математической модели с законами термодинамики.

• 4.    Количество фаз в формируемой математической модели должно быть произвольным.

анализируемого пространства.

Учитывая формулу (1) и обозначенные выше требования, можно использовать подход, описанный в трудах [18, 19], а именно термодинамические согласованные системы законов сохранения.

Подобная система будет выглядеть следующим образом:

_{=-   ∆} X ⁺ «Й , *0 ,                                                          (2)

где Q ( , ) – показатели датчиков в определённый момент времени; Ft 1 , F – гетерогенность потоков.

,

При подобном подходе системы можно выразить пространственно, в виде призмы с гиперболической поверхностью.

Q ( , ) может быть найдено экспериментальным путем, но Ft 1 , ^i-- могут быть найдены только с

, использованием методов для решения задач гиперболического типа. В работах [20–28] использован метод

Рунге – Кутты/WENO, также и в некоторых трудах в сочетании с модификациями TVD-схем и WENO- схем.

Рассмотрим многофазный поток, состоящий из двух фаз ( N = 2) [29]:

dps + dpSu^   0;

dt dXj^’ dpa1 । драник=0;

dt^Xk ’

^ + dt dx^

dpu_t + - ⁽ PUiUk+P²Ep+PWiEw_k ⁾ =0,  =1,2,3;

dtdx^

дрс. +    ^c i^uk+P^wfc) =0;

dtdx^

dp^wi   d ( WfcUk+E c i )

dt + dxi =0, где E – обобщенная внутренняя энергия многофазного потока, задающаяся как функция параметров те- чения.

Необходимо предусмотреть, что внутренняя энергия многофазного потока рассеивается (то есть осуществляет диссипацию). Модернизируем уравнение (3):

d_PS + _apSu^k =0;

dt dx^

dpa; dpaiuk _

+     =0, j =1,…, N -1;

dt      dx^

• +      ₌ 0;

dt dx^

dpu_ + dt

a( pu^lu^k+p²E_p8^l_k+pw^l_nE _k )

aPC1 + dt dpwj dt +

dx_k d ( P ^c J^ul+pE_wk )

=0, i =1,2,3;

dxk

d ( wju^l+E c j ) dx_k

=0, j =1,…, N -1;

=0, j =1,…, N -1.

Ключевым свойством данной системы уравнений является возможность представления состояния фазного потока в любой момент времени. Поскольку для относительных скоростей многофазного потока в данной системе выполняется тождество

dw^ dw^

ТГ -   =0, i =1,…, N -1; к , n =1,2,3.

dx^ dx/^

Продифференцировав его по X^ , мы получим

A dw^   Awj

( -^ -я )=0.

dt dxn   dx^

И это означает, что при условии t = 0, оно выполняется в любой момент времени t . Также система удовлетворяет основное термодинамическое тождество. Закон сохранения в системе уравнений (6), если

суммировать все его уравнения:

Q_W =  =  , я J =   ( =1,…, N -1),

Ho =  - SE_s - VE_v - ^cJ^Ecj -  2 ,

ul (I=1,2,3), в) =   ( =1,…,N-1), ]’k=ρ ^W^( =1, если умножить (7) на ρulEwk , то получим

-

ρ        -    =0

^, N -1),

и, записав уравнение в дивергентной форме dp( E+umun )   d(рик(Е-^тип^Пk)

dt               dx/t        =0,

где П – вектор потока энергии, который можно определить:

П к =    + u^kpw?E_wk + P^EcjE_wk ;

P =      .

Далее представим выражение (6) как производящий потенциал и переменные, что приведет систему в симметричную форму. Под производящими переменными мы понимаем такие переменные, которые наряду с консервативными вводятся относительно термодинамического преобразования Лежандра, чтобы выразить их относительно линейных функционалов некоего линейного пространства.

Для определения производящего потенциала L используем тождество

=(HwLqw + djLqi + doLqo + Щ^щ +     +     -l).(12)

В результате получаем:

• =   ; Lqi =    ; ^Qo = ; Ьщ =    ;    =

• L=      + Hj^qj + Ho^qo + ЩЬщ +     + Jk^p -p(e+     =     + pwfEw^ .(13)

J                                              J            JJ

Поскольку появилась возможность заменить уравнения системы на новые термины переменных и

производных, сама система примет вид:

^ +     =0; n= ,1,…, N - 1,0;

di ,    ^{3 ( u}\j⁺Jk^L,i-^skJ^J_nL,j ⁾

+ ------A---- {k =0;

dt              dx^

dLQj   d ( ^Bj+jj )

dt        dx^

dL j    d ( uⁿL j +6j )

+         =0.

dt        dx^

Ограничение запишется в виде dL : dL :

• -    =0.

dxn dxm

В этом случае закон сохранения энергии примет вид

Qw^qw + Qj^qj + QoLqo + Щ^щ + №j + ]ру_к - i) +

- dt \

^{+ dx}k {^ ^^^ ⁺ ^J^qj ⁺ ^o^qg ⁺ Щ^щ ⁺ ^j ⁺ ^^Lik} ⁺ Ik^ =0.

Тогда уравнение (14) представляем в эквивалентном виде:

^ + ^d- ⁽ t ⁾ sn =0; n =  ,1,…, N - 1,0 ;

. ^a(( u^kL ) I )

++ L.j XX -   =0;

dt dx^ J dx^ dx^

+ °- ⁽ иЧ ⁾ °J + V’k =0;

dt dx^ dx^

^Jk   a ⁽ A ⁾ Ji ■           _-        ■       ₌

V 1          -      +   =0

dt dxfc Jfi dx^ Jm ^^k dx^

Таким образом, полученная система удовлетворяет ряд поставленных требований:

• 1.    Система является гиперболичной при p [f + ЩпЩг^ .

• 2.    Все уравнения данной системы дивергентны.

• 3.    Модель создана в соответствии с законами термодинамики.

Данная система является удобной для построения вычислительного алгоритма на основе методов Рунге – Кутты/WENO в сочетании с модификациями TVD-схем и WENO-схем, условно обозначим их как RK-TVD и RK-WENO. Интеграция по времени осуществляется с помощью SSPRK (Strong Stability Preserved Runge–Kutta) [30], для описания прохождения потоков через границы используется метод GFORCE [31].

RK-TVD и RK-WENO реконструкции полученного уравнения будут производиться с лимитером типа minmod [32]. Сечение трубопровода считается постоянной величиной. Представим усреднённую модель:

=    ^{( u}- ) ₌ Q ( U );

dt dx              ;

⎛

U =

Pal agPg aiPi

\

^agPg^ug + ^IPl^-l I

⎝ Щ ^{- u}g ⎠

; F ( U )=

pct^u.

^agPg^ug dlppll ^agPg^ug^ug + скРьЩщ

\

,

\2

- ^ +  + PL -

Pl

^eg - ^ ^a Pg/

где u – вектор консервативных переменных; F ( U ) – вектор потоков; Q ( U ) – вектор правых частей

уравнения.

После обработки уравнения (18) методом Рунге – Кутты мы видим: dt ⁺      , _∆ X ^{, :} = ⁽ “ ) ₌ 0 ( Xi ^, U, );

^∆ X ⁼      ,5 - Xi-o ,5.

В приведенных обозначениях:

u° =   ;

u^l =     +I∆ tL ( u¹-¹ ), i =1,…, m -1;

u^m =∑ k=Q   , _kU^k + ^m ,    ( U™-¹ +I∆ tL ⁽ u™-¹ ));

uⁿ⁺¹ =   ,

где m = 2…n (по количеству фаз); a – корректирующие коэффициенты; U – значения решения, полученные на n-м уровне и временных слоях; ∆ t – шаг по времени, определяющийся конструктивными особенностями датчика, измеряющего параметр процесса.

Для реконструкции RK-WENO преобразовываем (19) в характеристическую форму системы для возможности в последующем записи системы в виде диагональной матрицы. Реконструкция будет выглядеть

+ B^=0,(23)

dt dx где В - матрица линеаризованных коэффициентов.

Приведем ее к диагональной форме с условием, что

V = Т U,(24)

где V - вектор характеристик переменных; Т - невырожденная матрица левой части системы.

Из этого следует:

+ D^=0,(25)

dt дх где D - диагональная матрица с собственными числами.

Поскольку реконструкция методом RK-WENO аналогична для всех компонентов У, то это означает, что, описав одну скалярную величину, используя принцип подобности, можно описать все оставшиеся скалярные величины. На практике это означает возможность изменения параметров модели с отсутствием потери в точности.

Исследуя ячейку [х / _ ₀, _s ,х t +о,_s ] как результат подобной реконструкции - Ту ₊₀, _s = Е(х i _ ₀, _s + 0), Ту _₀, s = Е(х i ₊₀ , _s — 0), вычислим индикаторы гладкости:

А 0 = - ( У — 2У ₊1 + v_{l+ 2} ) ² + -(3Ц — 4 У ₊1 + У ₊₂ ) ² ;

(26)

А, = - (У _ 2 — 2У _ 1 + У)2 +-(У _ 2 — 4 У _ 1 + ЗУ+2)2. 1Z

Функция индикаторов гладкости при данном разборе заключается в адекватности представления математического движения многофазного потока с учетом непрерывности производных.

Далее формируем нелинейные весовые коэффициенты:

^ = ^’ ^^,^ = 0,1,2.

Таким образом, найдя все значения У, вычисляем обратной заменой все значения U, так как они нужны для расчета реконструируемых потоков, по формуле

U = Т_1У.(28)

Сравним разработанные физико-математические модели с натурным поведением жидкости в трубопроводе лабораторного стенда [33].

Была проведена серия тестовых расчетов и тестовых запусков многофазного потока. Для удобства анализа сведем показания измерительных приборов (датчик скорости, датчик давления) в двумерную подстановку по Сода [34] и выразим их для удобства сравнения с имитационной моделью в относительных единицах. По оси ординат – показание датчика в относительных единицах, по оси абсцисс – время опыта. На рис. 1–3 представлены графические зависимости натурного эксперимента (NM) (динамика изменения параметра многофазного потока за время проведения теста) с результатами расчетов физикоматематической модели (PMM).

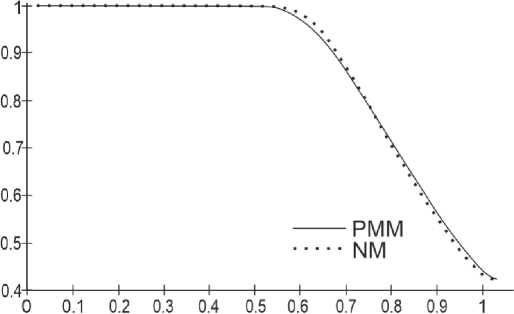
Рис. 1. Изменение плотности потока

Fig. 1. Change in flux density

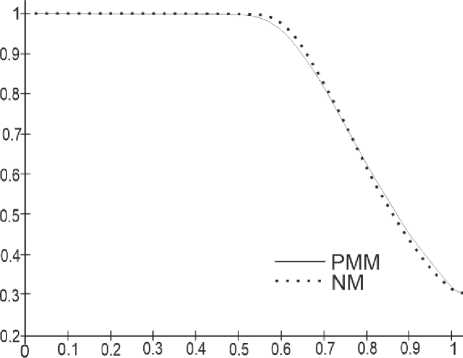
Рис. 2. Изменение давления на поток в различных участках системы лабораторного стенда Fig. 2. Change in pressure on the flow in different parts of the laboratory bench system

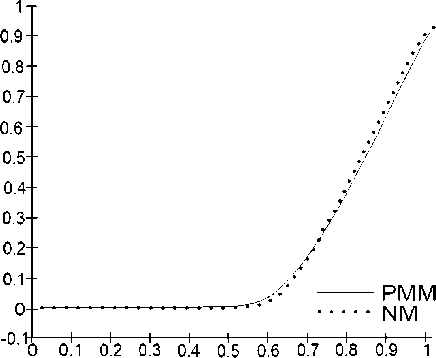
Рис. 3. Изменение скорости многофазного потока Fig. 3. Changing the speed of multiphase flow

По результатам графического сопоставления данных можно видеть, что разработанная физикоматематическая модель обладает высокой точностью имитации многофазного потока в лабораторном стенде.

Таким образом, рассмотрена возможность описания методики построения физико-математических моделей термодинамических процессов многофазных потоков наружных сетей теплоснабжения с использованием метода Рунге – Кутты/ WENO.

Перспективы использования результатов исследования в промышленности и практическая ценность работы

Результаты расчетов, проведенных для построения физико-математической модели, позволяют говорить о наличии согласованности полученной математической модели с законами термодинамики. Значит, на практике возможно использование данного метода для построения математической модели, позволяющей исследовать термодинамические процессы многофазных потоков наружных сетей теплоснабжения. Это позволяет исследовать влияние термодинамических процессов многофазных потоков наружных сетей теплоснабжения на саму систему теплоснабжения.

Рассматриваемая методика позволяет математически представить многофазный поток в виде

приходящего потока данных с однородным фоном, в перспективе удобным для детального рассмотрения, анализа и обработки с помощью информационных технологий.

В перспективе это означает возможность проектирования сверхсложных систем теплоснабжения (использующих многофазное рабочее тело в качестве теплоносителя) без потери точности при имитации. Данные разработки могут послужить ключевой технологией при разработке стратегии развития энергоснабжения и энергосбережения Арктических зон.

Выводы

Представлено нововведение в существующие TVD-схемы и WENO-схемы в виде описания представления математического движения многофазного потока с учетом непрерывности производных.

Это позволяет разрабатывать имитационные модели движения многофазной жидкости в трубопроводе с учетом параллельного изменения состава жидкостей и гладкости внутреннего диаметра трубопровода, что, в свою очередь, повышает точность имитации.

Разработанная в ходе данной работы методика может являться основой для создания плагина к библиотекам MATLAB Simulink и Simintech.