Разработка методики построения и исследования технологических систем в условиях автоматизации производства летательных аппаратов

Систематизация производственных процессов связана с решением задач упорядочения. Для определения и оценки исходных значений баз данных необходимо выполнить построение одной или более перестановок, удовлетворяющих определенным ограничениям и соответствующих экстремуму некоторых функций, определенных на рассматриваемом множестве значений параметров и начальных условий. Вариант перестановки можно представить последовательностью элементов из множества N={1,2,..., n}, или при символической записи в виде: π = (i1 , i2, . . . , in ), где in - элемент из N, занимающий в последовательности π k-e слева место в рассматриваемой последовательности мест К, или в виде матрицы ||xij|| размерности n x n, элементами которой являются числовые значения параметров процессов. При этом значение xij =1 соответствует записи (i, j), а сумма элементов в такой матрице, стоящих в каждой строке и каждом столбце, равна 1. Рассмотрим два n-мерных вектора (α = α1, α2,…,αn) и β = (β1,β2,…,βn), компоненты которых-действительные числа. Обозначим через π=(i1 , i2, . . ., in ) некоторую перестановку элементов множества N={1,2,..., n}. В этом случае построение оптимальных перестановок можно выполнить по формуле: f1 (π)= n f (п)^д ak ‘ вк . Покажем пример построения i=1

перестановки π* элементов множества N, кото- рой соответствует наименьшее значение f1 (π). Будем предполагать, что компоненты вектора α и β пронумерованы так, что α1 ≤ α2 ≤ ... ≤ αn.

Для расчёта и анализа вариативных показателей эффективности производства рассмотрим вариант перестановки π¹, отличающийся от варианта π транспозицией элементов i_k и i_k+1. При этом f₁(π¹) – f₁(π) = ( α _k – α _k+1)( β _ik+1 – β _ik). Если β _ik ≥ β _ik+1, то эта разность неотрицательна.

Таким образом, упорядочивая числа β _i в порядке их не возрастания, получаем искомый результат: π₁^* = (i₁^*, i₂^*,…, i_n^*), где β _ik^* ≥ β _ik+1^* для всех K.

Так как показатели эффективности зависят от граничных условий и целей исследования, условий работы конкретной ПС или входящей в неё ТС и системы управления, то эти показатели можно представить некоторой математической моделью, эквивалентной ПС, включающей отдельные требования и характеристики общей цели. Такое описание ПС может содержать целевое указание на связь между отдельными элементами системы и целевыми функциями в пределах общего влияния структуры системы на показатель эффективности, а также заданием условий её функционирования и связей между конкретными параметрами системы и составляющими показателей эффективности для вычисления количественных оценок этих показателей, используя данные о структуре и параметрах системы.

При исследовании общего влияния структуры на показатели эффективности рассмотрим характеристики структурной эффективности ТС производства при достижении многих целей с контролем, анализом и оптимизацией сразу нескольких выходных величин (рисунок 1). Общая система состоит из структурных входящих подсистем, которые описываются выражениями:

T j = Mxi,-, x m ) , j = 1,2, ^, r , где x_i – управляемые переменные; j_j – выходные переменные. Главная целевая функция зависит от локальных целевых функций, определяемых через j_j , от структуры связей между подсистемами, от вида функций j_j.

Пусть задача некоторой управляющей системы заключается в получении максимума выражения Ф( G – M), где G –ресурсы, а M – расход.

Если система может управлять двумя переменными: x₁ и х₂ , то имеем: G = f₁(x₁, х₂), M = f₂(x₁, х₂), тогда: max Ф (G - M) = max [f (х , х ) - f (х ,х )].

( x_t,3₂ ) ^{1 1 2} 2 1 2

В современных условиях развития автоматизированных производственных систем необходимо совершенствовать методологическую базу формализованного описания процессов и систем, позволяющую оперативно корректировать существующие знания и закономерности, на базе которых уже созданы и функционируют системы автоматизации ТС при условии, что процесс управления должен включать следующие элементы (рисунок 1).

Оптимизация производственных решений в такой системе необходима как на уровне проектирования и построения новых структур, так и в действующем производстве. В соответствии с иерархией производства предлагается исследование составляющих подсистем общей производственной системы как локально функционирующих структур с условием их оптимального синтеза в последующих процессах интеграции в единую систему и вычисления основных критериев функционирования.

На вероятностном уровне причинно-следственная связь между входной Xупр. и выходной Yвых. функциями для ТС устанавливается оператором Аt: y(t)=Atx(t). В блоке управления может реализоваться и обратный оператор:

At : x(t) = At y(t), так как в этом случае следствие y(t) выступает в роли причины, а причина x(t) – в роли следствия, что имеет значение в зависимости от постановки целей решаемых задач.

Иерархическая структура и характер функционирования ПС позволяют вводить количественные оценки эффективности взаимодействия её компонент в процессе построения адекватной условиям производства математической модели. Получение количественных и качественных оценок функционирования технологической системы связано с определением наиболее вероятных условий ее работы с учетом ограничений.

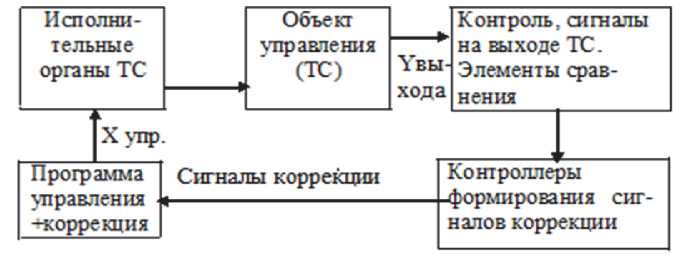
Рисунок 1. Блок-схема процесса многокритериального управления ТС производства в условиях автоматизации

Система условий производства имеет несколько обобщенный характер по отношению к объектам и предметам труда. Однако логично в постановке и решении задач принимать во внимание лишь те из этих условий, которые существенным образом влияют на основные исследуемые факторы и, соответственно, результаты: виды и объемы потребляемых ресурсов, реализуемые производственные и технологические схемы, в последующем действии, а также лишь некоторые из значений, принимаемых этими условиями. Целью такого подхода в исследуемом процессе является обособление системы. Соответствующее формализованное описание таких систем можно создать на основе систематизации граничных условий по целевому критерию решаемой задачи по методике, согласно которой предполагаем:

• -    число учитываемых условий равно Wr, где r = 1,2,...,t;(1);

• -    реализации упорядочиваются:

co < co < co , где S = 1,2,...,u для каждо-r min rs      r max, го из условий Wr(2).

• -    обособленную систему W , которая характеризуется упорядоченным множеством условий, можно представить в виде матрицы:

« 11 « 12 - « 1 u

W =	® 21    « 22    •••   « 2 u
	.           (3)

« t 1    « t 2   "•   « tu

Тогда для обеспечения определения наиболее вероятных по оптимальности условий необходимо (кроме значения условий реализации) знать вероятности (частоты) проявления условия W_r :

« 11

^ 21

^ 12

^ 22

Ц u

^ 2 u

E =

^U t 1     ^U t 2     •••    ^U tu

В матрице (2) u _s представляет собой вероятность (частоту) s – й реализации r – го условия.

Матрицу W в математической модели мы будем называть матрицей условий, а матрицу E – матрицей вероятностей.

Наиболее вероятные условия определяются в результате умножения элементов матрицы условий на соответствующие им элементы матрицы вероятностей с последующим суммированием произведений по строкам:

EW =

EW₁ EW ,

• ••

• ••

u

E   ^ 5 u 5

5 = 1

u

E ^ 5 ^

5 = 1

• ••

EWt

u

E

5 = 1

^5

Алгоритм расчётов общей суммы эксплуатационных и производственных затрат аналогичен получению по данной схеме общей зависимости производственных затрат. Однако эксплуатационные затраты в отличие от производственных зависят от времени, так как потребление ресурсов в эксплуатации происходит с течением времени эксплуатации, то есть в течение всей продолжительности последующего действия T V . Следовательно, потребление ресурсов будет выражаться показательными функциями, то есть как потребление, приходящееся на единицу времени. Обозначим такое потребление через N n _o . В этом случае суммарное потребление ресурсов в подготовительной части последующего действия составит N = N* или n_и = n *_ити . Для определения интегрального показателя эффективности производства и качества изделий и с учётом характеристики потребления в виде показательной функции рассмотрим наиболее общий случай определения эксплуатационных затрат.

Допустим, задано: i = k,r = t . Обозначим через n_u ir потребление ресурсов i - го вида при r-м условии, получим:

^п* и г =^[ g ( ^X )1 r / EW , .

Построим матрицу затрат ресурсов (4), в которой элементы этой матрицы представляют элементарные затраты: i-ая строка матрицы характеризует потребление i - ого вида ресурсов при наличии всех t условий, а ее r-й столбец – потребление всех видов ресурсов при r-м условии.

*          *

n u ll    n u 12

*           *

n u 21    n u 22

n u =

*

•••    ⁿ u 1 1

*

•••    n u 2 1

*

*

. n u k 1     n u k 2     •••    n u kt

После построчного суммирования элементов матрицы, имеющих одну и ту же единицу размерности, получим следующую матрицу затрат:

	X r = 1	* n u 1 r
n u =	t X r = 1	* n .2 r	.                 (7)

t

Е *

n u k

. r = 1

Умножая элементы матрицы (5), как и по методике с определением производственных затрат, на соответствующие им элементы матрицы (6) весовых коэффициентов, придающих одинаковую размерность всем видам ресурсов: d1

d 2

àk получим матрицу эксплуатационных затрат в стоимостном выражении:

t

E . *

nu1r r=1

t

E *

nu 2 r r=1

N и ak

t

X

r = 1

* n u * kr

Поскольку элементы этой матрицы имеют одинаковую размерность, их можно суммировать в виде (8):

- * k t

N u = X a i X n U r .        (io)

i = 1 r = 1

После преобразования получим:

- * t

^N u = X n u *r .            (11)

r = 1

ЗАКЛЮЧЕНИЕ

При таком подходе, учитывая возможность вариации вводимых ограничений при задании начальных условий по исследуемым производственным схемам, можно строить некоторое множество вариантов моделей с адекватными получаемыми результатами решений в диапазоне допустимых вариаций. Применительно к специфике производства такая методика позволяет вводить и оперировать с некоторым существенным множеством факторов при допустимой погрешности для определения ресурсов производственных и эксплуатационных мощностей по различным условиям эксплуатации и по подразделениям производства.