Разработка методики проектирования для расстановки опорных радионавигационных точек локальной навигационной системы, использующей сверхширокополосные сигналы

В настоящее время для навигации потребителей военного и гражданского сегментов широко используются глобальные навигационные спутниковые системы. Однако они имеют ряд недостатков, не позволяющих использовать такие системы в ряде практических задач. Как следствие, возникает необходимость создания и развития локальных на- вигационных систем (далее – ЛНС), способных обеспечить радионавигационное покрытие в условиях закрытых помещений. Наиболее целесообразным выбором для решения задачи навигации внутри помещений являются ЛНС, использующие сверхширокополосные сигналы (далее – СШП). Данный выбор объясняется прежде всего тем, что СШП-сигналы обеспечивают высокую разрешающую способность по времени [1].

Вне зависимости от базовой технологии и от измеряемых навигационных параметров (дальность, разность дальностей, псевдодальность, угол прихода сигнала или их комбинации) точность навигационных определений в позиционной СШП ЛНС существенно зависит от числа опорных радионавигационных точек (далее – ОРНТ) и их расположения относительно потребителя. Эту зависимость можно выразить в радиальной среднеквадратической погрешности (далее – РСКП), рассчитываемой по формуле

РСКП = ^ tr [ ( H T D-¹ H ) -1 ] , (1) где tr (...) – оператор взятия следа квадратной матрицы (суммы диагональных элементов); H – градиентная матрица, которая является производной вектора наблюдений навигационных параметров (дальностей, разностей дальностей, углов и др.) по вектору состояния (по координатам); D _ξ – матрица дисперсий первичных измерений.

Промышленные предприятия, которым, например, необходима система мониторинга сотрудников или система контроля доступа, имеют запрос не только на повышение точности навигационных определений, но и на снижение стоимости СШП ЛНС без потери качества ее работы. Этого можно достичь путем оптимизации числа ОРНТ и мест их размещения.

Если для помещения прямоугольной формы без препятствий задача квазиоптималь-ного по критерию минимального значения усредненного по помещению РСКП координатных определений размещения ОРНТ позиционной системы навигации имеет очевидное решение (равномерное размещение ОРНТ по периметру вокруг рабочей зоны), то в случае навигации внутри помещения с непрозрачными для радионавигационных сигналов стенами, перегородками задача расстановки ОРНТ сильно усложняется.

В общем виде не существует решения в аналитической форме задачи оптимизации размещения опорных точек (далее – ОТ), которое минимизирует РСКП координатных определений СШП ЛНС и их числа в рабочей зоне произвольной формы, поэтому метод решения выбирается из класса численных методов. Наиболее простым из вышеназванных методов решения задачи расстановки минимального количества ОТ при заданном РСКП координатных определений является прямой перебор всех возможных размещений ОТ, однако в непрерывном варианте задача имеет бесконечное количество решений. Данную задачу можно решить приближенно, разбив пространство помещения на дискретную сетку с шагом l, однако даже такой расчет имеет слишком большие вычислительные затраты.

Одним из перспективных численных методов оптимизации являются итерационные генетические алгоритмы. Генетический алгоритм (далее – ГА) – приближенный численный алгоритм, который для принципиально решаемой задачи при удачно подобранных значениях свободных параметров имеет тенденцию к сходимости, то есть к снижению РСКП координатных определений от итерации к итерации.

Считается, что генетические алгоритмы хорошо подходят для оптимизации функций многих переменных с множеством экстремумов. ГА не гарантируют отыскание глобального оптимума, но с высокой вероятностью отыскивают оптимумы, близкие по уровню к глобальному за короткое время (относительно малое число итераций), при этом требуют относительно небольших вычислительных ресурсов.

Разработка методики проектирования для расстановки опорных радионавигационных точек ...

Цель работы – создание программного обеспечения (далее – ПО) для расстановки ОРНТ внутри СШП ЛНС на базе ГА с целью минимизации затрат на развертывание и поддержание структуры СШП ЛНС.

Материалы и методы

ГА были предложены 1975 году, их базовый принцип – эвристическая имитация природного естественного отбора наиболее приспособленных особей, отличающихся уникальными наборами генов, из всей популяции особей. При этом путем скрещивания особей появляется потомство с новыми уникальными наборами генов и вытекающей из него собственной приспособленностью [2].

ГА показали способность к быстрому обнаружению квазиоптимальных решений при сравнительно невысоких вычислительных затратах. Среди недостатков ГА можно выделить большое разнообразие методов отбора особей (равновероятный выбор, выбор после превышения некоторого порога показателей качества с вероятностью, пропорциональной показателю качества, и др.) их последующего скрещивания (сколько особей участвует, сколько участков хромосом подвергаются обмену, в каких точках устанавливаются границы обмена, сколько мутаций происходит при скрещивании и с какой вероятностью ), процедур отбора особей в популяцию на следующей эпохе (отбор M лучших особей, отбор с пропорциональной показателю качества вероятностью, отбор только новых особей или возможность «старым» особям сохраниться в популяции и др.), организации популяций (унитарная популяция, острова с непересекающимися популяциями, острова с циклически пересекающимися популяциями и др.), в результате чего возникают свободные параметры [3], которые разработчик задает случайным образом.

Особями в данной работе являются варианты размещения ОТ, хромосомами (векторами состояния) – наборы координат ОТ, генами – координаты отдельных ОТ.

Скрещивание в данном случае – это процедура случайного смешивания наборов координат с получением координат размещения ОТ в результате нового случайного набора. Мутации генов [4] – это случайные искажения изначальных вариантов координат после скрещивания.

В основе ГА лежит представление области решений в виде случайной выборки из M ~10¹..10² значений вектора { x N 1 , x N 2 ,..., x N _M } [5].

Перед инициализацией задают план помещения – рабочую зону СШП ЛНС с привязкой к системе координат – и разбивают ее координатной сеткой с некоторым шагом l . Также задаются начальным числом N _OT . При инициализации (на нулевой итерации генетического алгоритма) случайным образом формируют выборку M ~ 10¹..10² векторов x N 1₀, x N 2₀,..., x N _M , каждый из которых задает вариант размещения N _OT в двумерной координатной сетке.

На каждой i -й итерации работы ГА на основе нелинейного случайного преобразования векторов (имитирующего кроссинговер – природный механизм обмена генами, отсюда название алгоритма) из предыдущей выборки происходит формирование новой промежуточной выборки объемом R ~10²..10 4 M векторов такой же размерности N х 2 .

Преобразование векторов заключается в следующем: случайным образом выбирают пару векторов из предыдущей выборки:

от        от от     от от       от от т xN ik-1 =[(x1 ,У1 )i 4x2 ,У2 )i v"4xN ,yN )i JH

T

от xN jk-1

/ от от\ ( от от\    (от от\

= ( x 1 , У 1 ) j 4 x 2 , У 2 ) j >->( ^xN ,y N ) j J

,

где i ^ j - индексы векторов в выборке; ( x °^T , y °^т ) - координаты v-й ОТ, v = 1,2,..., N .

TT T

от x Ni k —1

от xN jk-1

T

^J k -1

T T ■

где

J k -1

■⁺ k -1

от от от от

' 1 , У 1 ) i 4 x 2 , У 2 ) i v-j

T от от xN ,yN I. I

от от от от      от от xn+1, Уп+1 ) i 4xn+2, Уп+2 )i ■’•”4xN , yN

/ от от\ ( от от \ Оот от \ = ( x 1 , У 1 ) j >( ^x 2 , У 2 ) j ’’Ц ^xN , y N )

k -1

T

^J k -1

T

'j J k -1 ’

T

/ от \=       ( от от \ ( от от\    (от от \

\xN j/ к -1 =[ \ x n +1 , У п +1 ’ j 4 x n +2 , У п +2 ’ j ’’’A x N ^, y N ’ j J^

.

Далее из первой половины i -го вектора и второй половины j -го вектора формируется новый предварительный вектор новой промежуточной выборки:

- тт s Nr k

TT x^тт V О^⁷ г x N i , x N j

T

I k-1

где r = 1,2,

R – индекс векторов в новой промежуточной выборке.

Новый предварительный вариант размещения ОРНТ образуется в виде случайного

сочетания двух предыдущих: размещение первых n ОРНТ берется из вектора x N ^T i , а размещение оставшихся N - n ОРНТ - из вектора x N ^T j .

• - ^тт

Далее предварительный вектор s_Nr подвергается еще одному случайному нелинейному преобразованию: с вероятностью p координаты случайно выбранной ОРНТ

• т от                              - тт                                    ' тт ' от

I x v , y v I , v = 1,2,..., N в составе s_N r_t заменяются на случайные I x v , y_v I в пределах рабочей зоны (тем самым имитируется природный механизм мутаций), в результате чего образуется новый вектор новой промежуточной выборки s N _r . То есть в предварительном варианте размещения ОРНТ s^ , который составлен из частей предыдущих размещений x N ^T i и x N ^T j , с вероятностью p размещение одной из ОРНТ меняется случайным образом, образуя новый промежуточный вариант размещения.

Таким образом, ГА – численный алгоритм, который для принципиально решаемой задачи при удачно подобранных значениях свободных параметров имеет тенденцию к сходимости, то есть к снижению РСКП координатных определений внутри рабочей зоны. При стабилизации достигнутого показателя качества в течение нескольких итераций де-

Разработка методики проектирования для расстановки опорных радионавигационных точек ...

лается заключение о том, что с высокой вероятностью достигнута квазиоптимальная расстановка. Максимальное число итераций генетического алгоритма является свободным параметром.

ГА имеет 22 входных параметра (см. Таблицу 1), часть из которых существенным образом влияет на исход работы алгоритма.

Таблица 1

Набор входных параметров ГА

№	Обозначение	Тип	Содержание
1	M 0	целое > 0	Начальная численность популяции
2	M уст	целое > 0	Установившаяся численность популяции
3	α	≥ 0	Параметр скорости снижения численности популяции
4	L 0	целое > 0	Начальная численность потомков
5	L ycm	целое > 0	Установившаяся численность потомков
6	β	≥ 0	Параметр скорости снижения численности потомков
7	ε	≥ 0	Параметр скорости переключения между алгоритмом 2 и 3 подбора родителей
8	Q	целое > 0	Число особей-родителей, участвующих в размножении
9	R	целое > 0	Число точек разрыва хромосомы при размножении
10	A	целое > 0	Число потомков в одном размножении

Источник: здесь и далее таблицы составлены авторами.

Для анализа влияния того или иного свободного параметра были проведены соответствующие эксперименты: производился запуск нескольких ГА при изменении только одного параметра.

Так, например, параметр скорости снижения численности потомков не влияет на исход работы ГА (см. Рисунок 1).

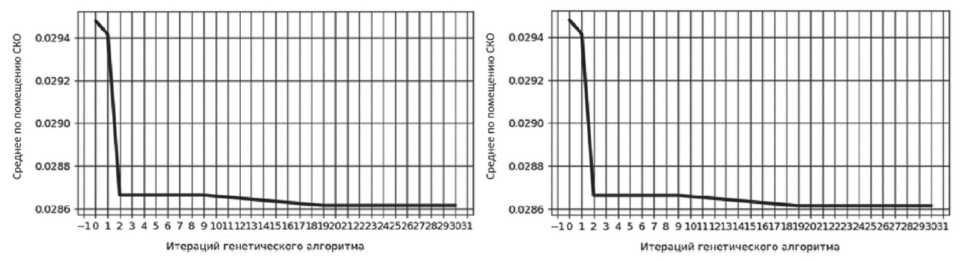
Рисунок 1. Итог работы ГА при параметре скорости снижения численности потомков 0,2 (слева) и 0,5 (справа)

Источник: здесь и далее рисунки выполнены авторами.

В свою очередь, СКО вариации координаты уже влияет на исход работы ГА (см. Рисунок 2).

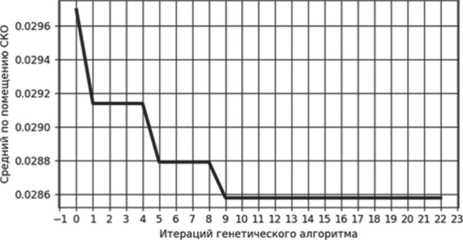
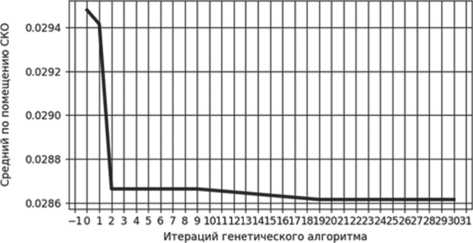
Рисунок 2. Итог работы ГА при СКО вариации координаты 0,25 (слева) и 0,5 (справа)

Таким образом, было получено, что на исход работы ГА влияют следующие параметры:

• •    начальная численность популяции;

• •    установившаяся численность популяции;

• •    установившаяся численность потомков;

• •    число особей-родителей, участвующих в размножении;

• •    число точек разрыва хромосомы при размножении;

• •    параметр скорости переключения между алгоритмом 2 и 3 подбора родителей;

• •    СКО числа заменяемых генов;

• •    СКО вариации координаты;

• •    доля элитных особей в элитарном отборе;

• •    коэффициент терпимости к ухудшению показателя качества алгоритма отбора вытеснением;

• •    установившееся значение температуры в алгоритме отбора методом отжига.

Синтез генетического метаалгоритма

Принципиальным недостатком ГА, как уже говорилось выше, является относительно большое разнообразие вариантов процедур и относительно большое число свободно назначаемых параметров при отсутствии рекомендаций по их выбору. Неудачный выбор параметров в конкретной реализации ГА может привести к невозможности достижения требуемому РСКП координатных определений.

Для численного решения задачи оптимизации параметров ГА под задачу определения мест размещения ОРНТ СШП ЛНС предлагается применить генетический метаалгоритм [6] (далее – ГМА), объектами работы которого будут метаособи в виде векторов параметров ГА.

Ниже приведена блок-схема ГМА (см. Рисунок 3).

Для оптимизации параметров ГА с помощью ГМА была создана выборка из пяти планов помещений, различающихся соотношением сторон, содержащих «сложные» препятствия: объекты в центре комнат, коридоры. Предполагается, что данная выборка достаточно репрезентативна для получения настройки входных параметров ГА, эффективно справляющегося с оптимизационной задачей размещения ОРНТ СШП ЛНС по помещению любого типа.

Разработка методики проектирования для расстановки опорных радионавигационных точек ...

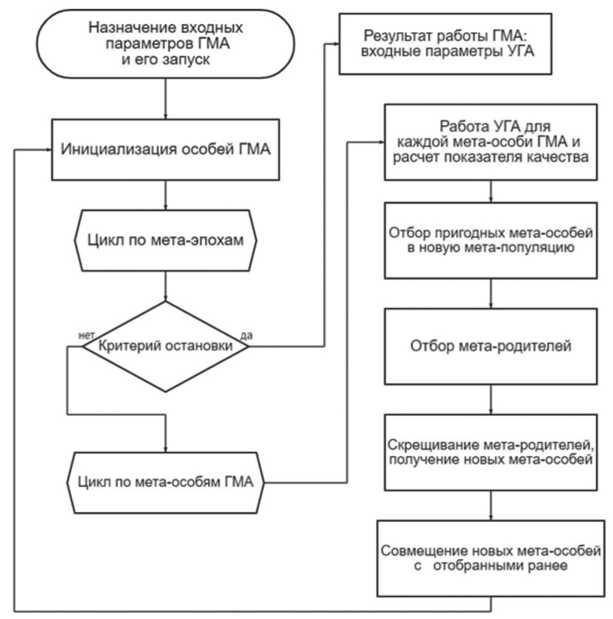
Рисунок 3. Блок-схема генетического метаалгоритма

Показатель качества для одной комнаты будет вычисляться следующим образом:

E = k a ,

где k - число эпох ГА, за которое алгоритм достиг требуемой точности, а a [7] a =— JJ a ( x , y ) dxdy ,

S

Тогда показателем качества особи ГМА будет среднее арифметическое показателей качества каждой комнаты:

N

Z E

где N – число различных комнат.

E = - n =1--- , N

На выходе ГМА получаем набор параметров (см. Таблицу 2), при котором наблюдается сходимость, показанная на Рисунке 4.

Таблица 2

Значения оптимальных параметров ГА

Параметр ГА	M 0	M vcm	L vcm	Q	R	£	а зам	а коорд	п	и	t vcm
Значение параметра	27	13	11	4	5	0,69	1,95	0,99	0,56	1,99	47

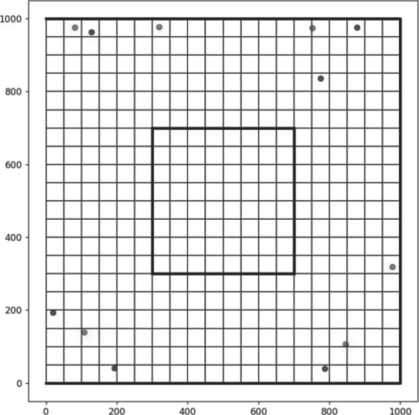
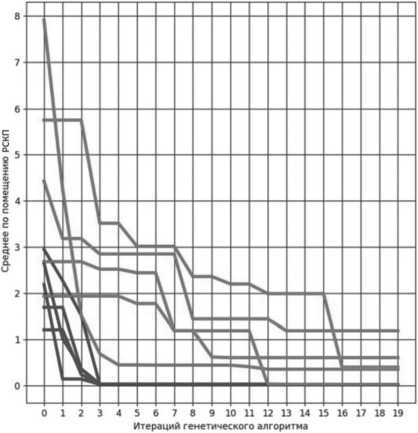
Рисунок 4. Сходимость ГА без предварительной настройки (красный цвет) и с предварительной настройкой (синий цвет); данный план помещения не участвовал в ГМА

Как видно на Рисунке 4, ГА с предварительной настройкой сходится к требуемому значению РСКП координатных определений быстрее (за меньшее число эпох), чем с выбранными случайным образом входными параметрами.

Задачей ГА в данной работе является получение квазиоптимальных координат расположения ОРНТ СШП ЛНС для уменьшения финансовых затрат на развертывание и поддерживание инфраструктуры СШП ЛНС [5]. Явным преимуществом ГА с предварительно настроенными входными параметрами с помощью ГМА является отсутствие необходимости привлечения высококвалифицированных специалистов.

Разработка программного обеспечения

В данной работе было разработано ПО (см. Рисунок 5), в котором разработчику предоставляется возможность выбора числа ОТ, позиционного метода, способа ограничения ГА по количеству эпох или по достижению РСКП координатных определений.

Рисунок 5. Интерфейс ПО

Разработка методики проектирования для расстановки опорных радионавигационных точек ...

Одной из возможностей ПО является расстановка ОРНТ разработчиком самостоятельно, пример интерфейса представлен на Рисунке 6.

Для работы с необходимым планом помещения нужно подготовить файл через конвертер из формата dxf программы AutoCAD (см. Рисунок 7).

Разработанная программа позволяет работать с препятствиями различной формы (любой многоугольник и/или окружность).

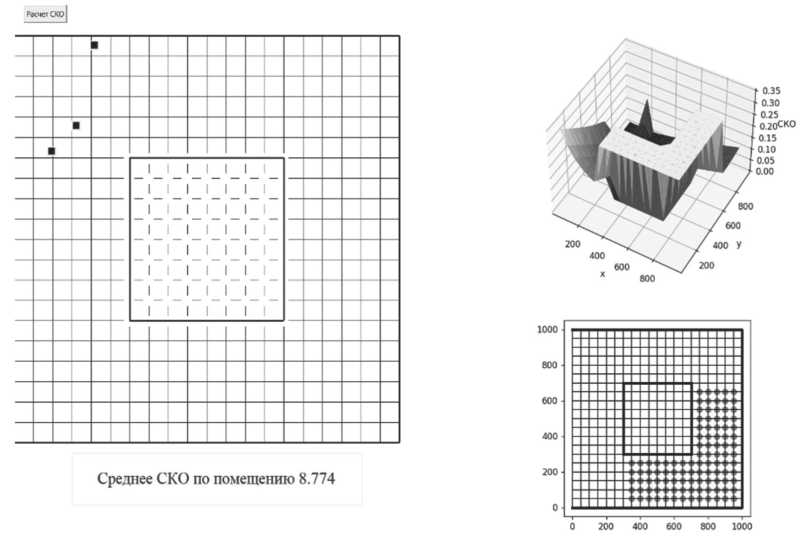
Рисунок 6. Окно расчета РСКП при постановке ОРНТ вручную (красным обозначены области, в которых отсутствует прямая видимость между ОРНТ и потребителем)

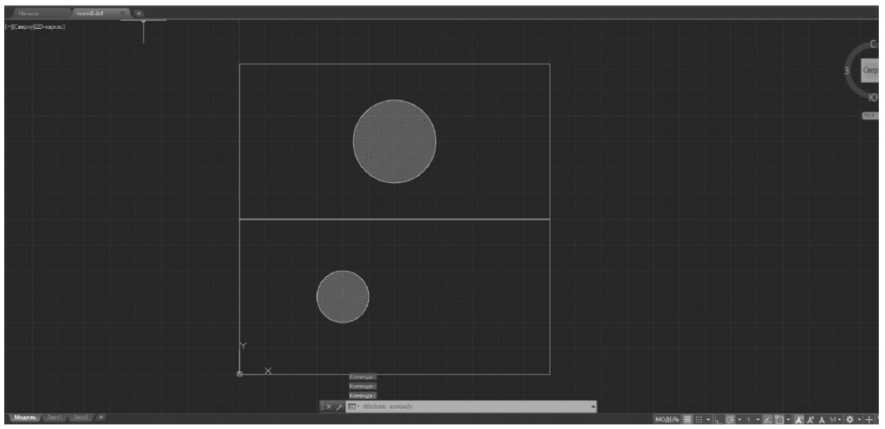
Рисунок 7. Рабочее пространство в среде AutoCAD

Определение видимости ОРНТ области пространства основано на наличии пересечения отрезка, соединяющего ОРНТ и потребителя, с отрезком, являющимся частью препятствия. Если хотя бы с одним из препятствий есть пересечение, видимость между ОРНТ и потребителем отсутствует.

При нажатии на кнопку «Запустить оптимальный ГА» (см. Рисунок 5) вызывается окно расчета ГА с предварительно настроенными входными параметрами с помощью ГМА (см. Рисунок 8), которое будет обновляться с каждой итерацией ГА, то есть с каждой эпохой в реальном времени.

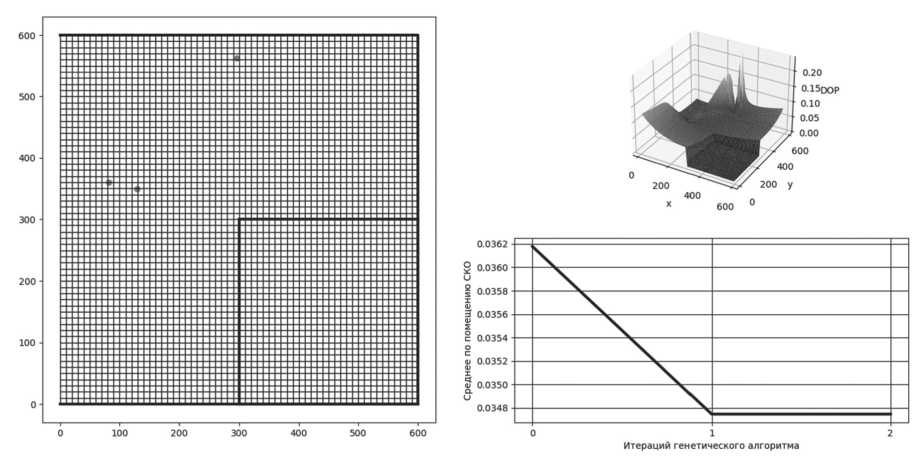
Рисунок 8. Окно расчета ГА с предварительно настроенными входными параметрами с помощью ГМА

Работа ГА с предварительно настроенными входными параметрами с помощью ГМА позволяет получить расположение ОТ, при которых достигается не только требуемая погрешность СШП ЛНС, но и минимальное число ОТ, что позволяет существенно снизить стоимость СШП ЛНС.

Блок-схема алгоритма поиска наименьшего числа ОТ, при котором достигается заданное значение усреднённого по помещению РСКП координатных определений, приведена на Рисунке 9.

Для данного плана помещения производится численный оптимизационный поиск наименьшего числа ОТ, при котором достигается заданное значение усредненного по помещению РСКП координатных определений.

Поиск расстановки осуществляется соответствующим числом реализаций минимум по 30 итерациям (эпохам) в каждом (после этого задействуется критерий останова, если показатель качества, достигнутое усредненное по помещению РСКП координатных определений, не уменьшается в течение 10 эпох).

Задача определения координат ОРНТ ранее решалась специалистами интуитивно на основе их личного опыта и квалификации. В настоящей работе предложено решать эту задачу с помощью численной оптимизационной процедуры с предварительно настроенными входными параметрами с помощью ГМА. Так как получение аналитических соот-

Разработка методики проектирования для расстановки опорных радионавигационных точек ...

ношений для сравнения эффективности не представляется возможным в силу большой вариативности планировки помещений, оценка эффективности произведена экспериментально.

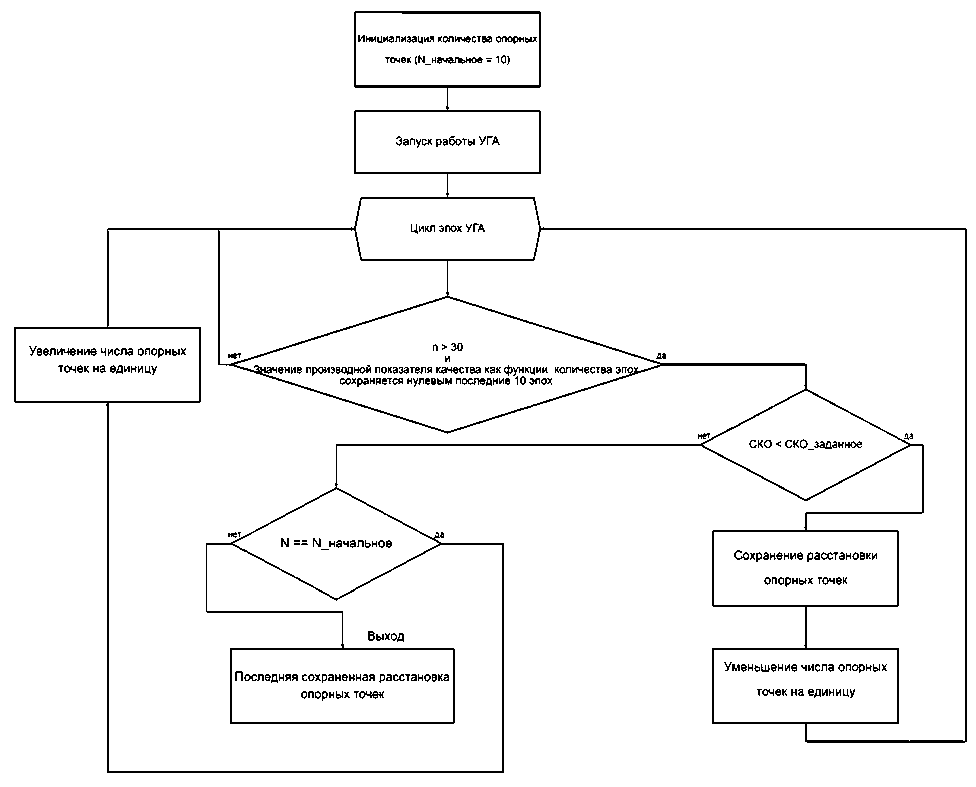
Рисунок 9. Блок-схема поиск наименьшего числа ОТ

СКО «сырых» измерений радионавигационных параметров были измерены экспериментально (см. Рисунок 10). Эти оценки используются для определения значений матрицы дисперсий измерений D _ξ при расчете РСКП координатных определений в соответствии с выражением (1).

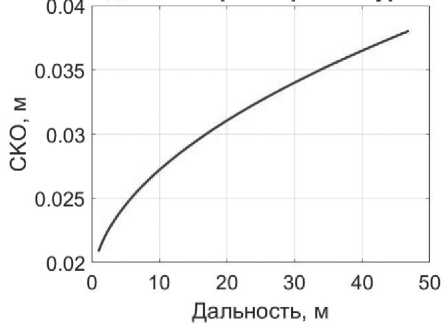
Рисунок 10. Зависимость СКО случайной погрешности от дальности

Натурный эксперимент

Эксперимент заключается в следующем. Задан план помещения, содержащего следующие элементы: колонны, коридоры, стеллажи (см. Рисунок 11). Поставлена задача определить минимальное число ОРНТ NОТ и соответствующие координаты их размещения для дальномерного позиционного метода СШП ЛНС, при которых расчетное значение РСКП координатных определений, определяемое по выражению (1), для 90 % площади помещения не превышает его требуемый уровень, установленный для определенности равным 1 м.

Для исключения сингулярностей значение распределения РСКП координатных определений σ (х, у) для тех участков помещения, в которых не обеспечивается видимость минимально необходимого для решения навигационной задачи числа ОРНТ, ограничивалось сверху максимальным значением линейного размера рабочего пространства max ( РСКП ( x , y ) ) = 25( м ) . Это значение обусловлено предположением, что отслеживаемый объект не выходит за границы помещения и потому погрешность его координатных определений не превышает типовых значений размеров помещения промышленного назначения.

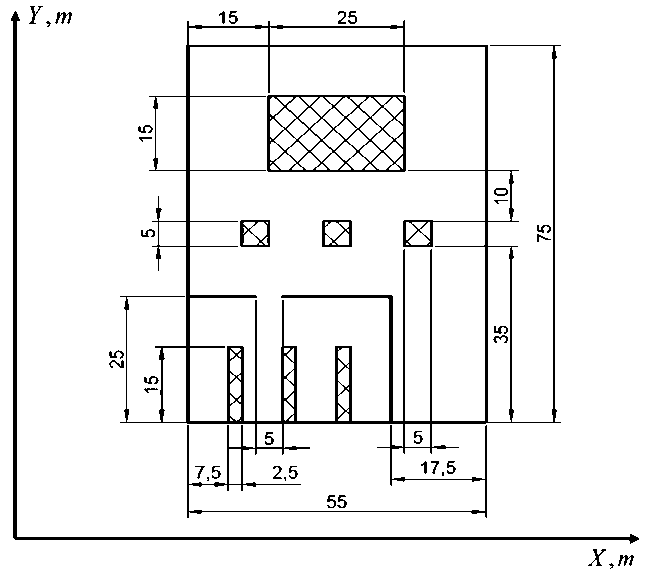
Рисунок 11. План помещения для сравнения эффективности разработанного алгоритма и традиционного эвристического подхода

Разработка методики проектирования для расстановки опорных радионавигационных точек

Поставленную задачу независимо друг от друга решили семеро специалистов, имеющих опыт от 1 до 5 лет в радионавигации вообще и в разработке и испытаниях СШП ЛНС в частности, а также задача была решена автоматически с применением ГА в двух вариантах: со случайно выбранными значениями параметров и с параметрами, оптимизированными с помощью ГМА. Ниже приведены результаты эксперимента для дальномерного позиционного метода СШП ЛНС [7; 9] (Таблица 3).

Таблица 3

Результаты размещения ОРНТ запросной дальномерной СШП ЛНС специалистами и генетическими алгоритмами

	Время, затраченное на проектирование, мин	Число опорных точек	РСКП, м
Специалист 1	30	17	2,281
Специалист 2	5	14	5,398
Специалист 3	15	18	1,712
Специалист 4	35	17	0,816
Специалист 5	210	24	0,027
Специалист 6	35	17	4,143
Специалист 7	40	23	0,357
ГА со случайными параметрами	50	16	0,974
ГА с настройкой	40	15	0,761

Данные Таблицы 3 представлены в форме диаграммы на Рисунке 12.

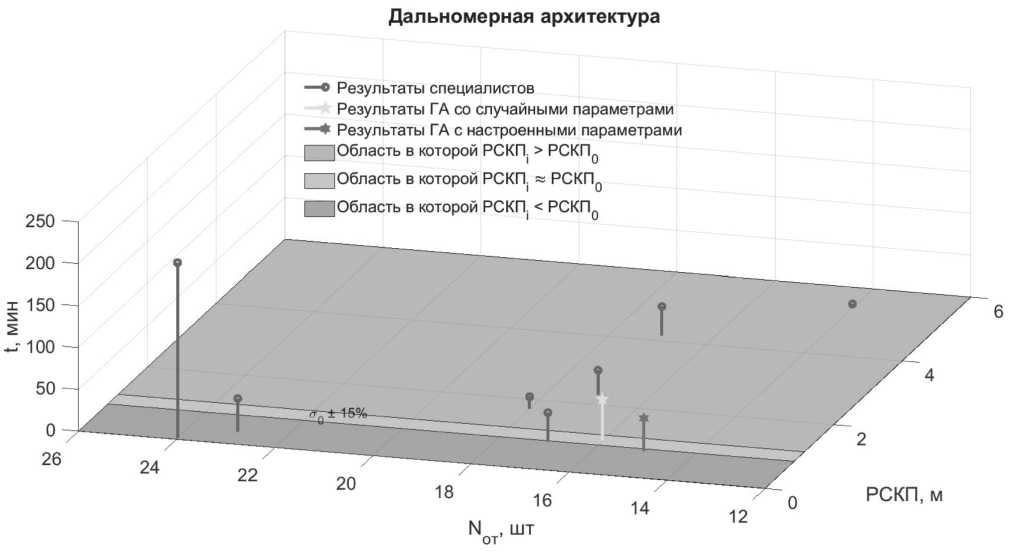
Рисунок 12. Результаты проектирования для запросной дальномерной СШП ЛНС

Как видно из Таблицы 3, ГА с настройкой справился с задачей, используя меньшее количество ОТ, что является приоритетным действием, так как при этом снижается сложность СШП ЛНС при сохранении ее качества.

Заключение

Таким образом, разработано ПО для расстановки ОРНТ СШП ЛНС на базе ГА с предварительно настроенными входными параметрами с помощью ГМА. Также реализована возможность расстановки ОРНТ СШП ЛНС разработчиком вручную.

Разработан алгоритм поиска наименьшего числа ОРНТ СШП ЛНС, при котором достигается заданное значение усредненного по помещению РСКП координатных определений. Эффективность разработанного алгоритма подтверждена экспериментальным сравнением его результатов с результатами проектирования опытными специалистами. Только три специалиста из семи справились с задачей, используя при этом в среднем на 5 ОРНТ больше, чем использует ГА с предварительно настроенными входными параметрами с помощью ГМА, что существенно осложнило бы архитектуру СШП ЛНС и увеличило бы стоимость ее развертывания и поддержания.