Разработка методики токовой диагностики асинхронных двигателей по осциллограммам нестационарных режимов работы

Создание современных энергосберегающих электротехнических систем тесно связано с вопросами повышения надежности эксплуатации электроприводов технологических агрегатов и вызывает необходимость осуществления постоянного мониторинга состояния электродвигателей. При этом можно воспользоваться различными методами диагностики состояния двигателя. Одним из эффективных является метод, основанный на спектральном анализе потребляемого двигателем тока [1, 2]. На его основе появляется возможность определять состояние различных элементов двигателя и выявить наиболее распространенные неисправности:

• •    повреждения ротора (обрыв стержней, ослабление крепления стержней к контактным кольцам, скрытые дефекты литья);

• •    повышенный эксцентриситет ротора (статический и динамический);

• •    межвитковые замыкания обмоток статора;

• •    повреждения подшипников;

• •    несоосность валов двигателя и механической нагрузки;

• •    дефекты механической части связанных с электродвигателем устройств.

Каждый дефект и неисправность вносят в картину процесса электропотребления свои особенности, а именно изменения основных характеристик сигналов. Действительно, любые «возмущения» по состоянию электрической и механической части электродвигателя приводят к изменениям магнитного потока в зазоре электрической машины и, следовательно, к модуляции потребляемого тока. Таким образом, наличие в спектре тока двигателя характерных (и несовпадающих) частот определенной величины свидетельствует о наличии или появлении отмеченных выше дефектов.

Преобразование Фурье, как известно, позволяет осуществить гармонический анализ стационарных режимов, удовлетворяющих условиям Дирихле. При этом для достоверного диагностирования состояния электродвигателя необходимо осу- ществлять экспресс-обработку осциллограмм статорного тока относительно большой длительности при постоянной частоте и слабо меняющейся нагрузке. Для двигателей, постоянно работающих в динамических режимах (частые пуски и торможения), данный метод непригоден. В этой связи необходимо рассмотреть возможности других методов обработки сигналов, включая самые современные, основанные на компьютерных технологиях.

В динамических режимах, когда многократно возрастают нагрузки во всех узлах электродвигателя многие дефекты, даже на стадии развития, проявляются более заметно в токовых и акустических сигналах. Для их распознавания необходимо создать библиотеку (базу данных) признаков той или иной неисправности на основе математической обработки осциллограмм статорного тока. Необходимо отметить, что методологические аспекты подобного рода процедур диагностирования в настоящее время находятся в развитии. Одним из перспективных направлений являются компьютерные исследования на моделях электромеханических устройств, в составе которых удается имитировать различные дефекты.

В настоящее время известные модели двигателей достаточно точно отражают характер протекания электромагнитных и электромеханических процессов в заведомо исправном электродвигателе и не позволяют исследовать влияние различных дефектов и неисправностей на основные характеристики двигателей. В этих условиях актуальной становится задача разработки новых моделей электродвигателя, на основе которых реализуется возможность проведения исследований влияния на контролируемые параметры различных неисправностей.

При разработке универсальной модели предлагается воспользоваться методом конечных элементов (finite-element method) [3, 4, 6], позволяющим осуществить расчет картины магнитного поля в поперечном сечении машины для каждого момента времени с учетом предыстории процесса. В основе этого метода лежит разбиение расчетной области сеткой конечных элементов, чаще всего треугольников, как это показано на рис. 1 для поперечного сечения асинхронного двигателя с короткозамкнутым ротором. Значения характеристик поля рассчитываются либо в узлах сетки, либо в центре тяжести каждого конечного элемента.

Чаще всего магнитное поле в пределах активного пространства двигателя представляется плоскопараллельным, то есть в любом поперечном сечении машины картина поля остается неизменной. Данный метод позволяет точно учитывать геометрию машины в ее поперечном сечении, а также электрические параметры двигателя, включая нелинейность кривой намагничивания и другие особенности, как например, возможные дефекты в магнитной и витковой системе электрической машины. Метод конечных элементов позволяет осуществить расчет мгновенной картины магнитного поля по заведомо известным значениям плотностей тока в пазах статора и ротора. В этой связи представляет интерес разработка конечноэлементной модели асинхронного двигателя, позволяющей непосредственно рассчитывать значения плотностей токов в каждый момент времени, исходя из динамически меняющейся картины магнитного поля, мгновенные значения которого, в свою очередь, зависят от значений плотностей тока в каждый конкретный момент времени.

Как известно, электромагнитное поле описывается системой уравнений Максвелла [3, 5], которую применительно к теории электрических машин можно записать в виде:

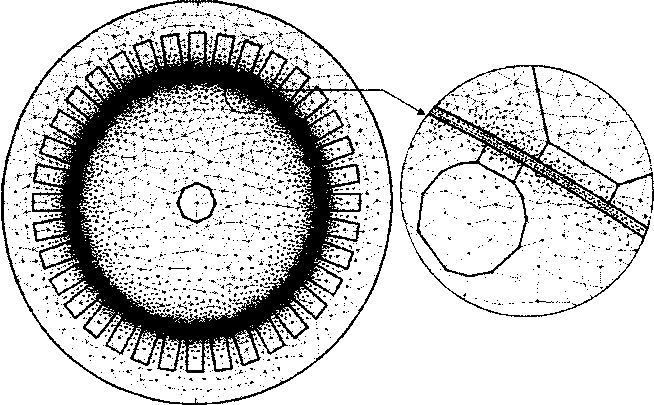
Рис. 1. Расчетная область поперечного сечения асинхронного двигателя с сеткой конечных элементов

rotH = j;

^ ЗВ rotE --;

St j  p ^+ j cmop ’

div В = 0.

"в = ван;

Данные уравнения являются общеизвестными в теории электротехники и не нуждаются в дополнительных комментариях.

Мгновенную картину плоскопараллельного электромагнитного поля в поперечном сечении асинхронного двигателя можно описать скалярным неоднородным уравнением Гельмгольца [3]:

• 1    Э²^    ¹ X оА _ .

ВоВ Зх1 + р6ц ду2 р St Зс”°р'

Данное уравнение является прямым следствием системы уравнений (1) и записывается относительно векторного магнитного потенциала поля

• А, ротор которого равен индукции магнитного поля в данной точке [3]:

В = rot А.                                 (3)

Поскольку поле плоскопараллельное, то при ориентации оси z системы координат параллельно оси вала машины, вектор индукции магнитного поля В будет лежать в плоскости хОу, поперечного сечения машины. Тогда согласно первому и третьему уравнениям системы (1) и уравнению (3) -> вектор плотности тока проводимости j и вектор ный магнитный потенциал А будут параллельны оси z. Это позволяет перейти от векторов к скалярным величинам в уравнении (2).

Плотность тока и значение векторного магнитного потенциала в пределах каждого отдельного конечного элемента расчетной области представляются неизменными. Следовательно, внутри каждого конечного элемента электромагнитное поле можно описать уравнением (3). Для того чтобы описать полную картину поля, необходимо решить систему, состоящую из уравнений вида (2), размерность которой равна числу конечных элементов. Задача усложняется тем, что каждый раз при изменении угла поворота ротора меняется геометрия расчетной области и это приводит к необходимости переопределять сетку конечных элементов. Решение уравнений параболического типа, к которому относится уравнение (2), методом конечных элементов на непостоянной сетке является сложной задачей. Чтобы упростить ее, представим частную производную по времени от векторного магнитного потенциала в виде конечной разности [4]:

9t At ’ где А - значение векторного магнитного потенциала в рассматриваемой точке на данной итерации, Ао - значение векторного магнитного потенциала в той же точке на предыдущей итерации, At - дискрета времени.

Используя второе и четвертое уравнения системы (1) и уравнение (3), плотность тока проводимости, обусловленного явлением электромагнитной индукции, можно выразить через векторный магнитный потенциал:

• 1         1 а^

j= —Е =--- р     р Ot

Плотность стороннего тока проводимости устор в каждой точке проводника, помещенного в переменное магнитное поле, может быть представлена как результат действия суперпозиции электрических полей, возникающих в других областях, электрически связанных с рассматриваемой точкой, вследствие явления электромагнитной индукции либо под действием внешних источников ЭДС. Стержни короткозамкнутого ротора электрически соединены друг с другом контактными кольцами. Следовательно, для /-го конечного элемента, ле- жащего внутри одного из пазов ротора, плотность стороннего тока проводимости может быть представлена как функция от производных векторного потенциала по времени в других конечных элементах, лежащих внутри пазов ротора:

; = f(^B. ^iL ЗА^ ЗАгМ Jcmopi ’ 9t v 9t , 9t 9t A где Ar - векторный магнитный потенциал произвольного конечного элемента, лежащего внутри одного из пазов ротора, М- общее число конечных элементов, лежащих внутри всех пазов ротора.

На плотность стороннего тока в статорных обмотках помимо явления электромагнитной индукции в каждый момент времени оказывают влияние мгновенные значения фазных ЭДС питающей сети двигателя. Следовательно, аналогично для j-ro конечного элемента, лежащего внутри одного из пазов статора:

5Asl 8As2 ®Aj-i ^sj+i v 3t ’ 3t at ’ at

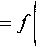
где A_s - векторный магнитный потенциал произвольного конечного элемента, лежащего внутри одного из пазов статора, N - общее число конечных элементов, лежащих внутри всех пазов статора, е_а, вы е_с - мгновенные значения фазных ЭДС питающей сети двигателя.

Согласно (2), (4), (6) и (7) систему уравнений для расчета значений векторного магнитного потенциала во всех конечных элементах расчетной области в каждый момент времени можно представить в виде:

1 а²л^ _{ 1 а²^- 1 л_п -4п _ ц₀ ах² ц₀ ар² Рг

_ _ Д ^r\ ~ А)г1 ^г2 ^— A)r2

At ’ At            At

At ’АГ )

1 ^ ^sj 1 ^ A j   1 A j Asj _

Ц₀ ax² Цо oy² P_s Ar

Al^^Osy A2 ^- As2  Aj-4^AsJ-l

АГ ’ АГ             АГ

^A2j^l^2A2±L ^^sN ^^sN _e e e г

АГ ’ Ar a’ b’ c )

женной через угол поворота ротора:

da> а^гф -ф^ + гф^-ф

dt dt2 (аг)2      ■                 (10)

где ф - угол поворота ротора на текущей итерации;

^о ? ^оо ” У10-™ поворота ротора соответственно на предыдущей и предпредыдущей итерациях.

Подставив выражение (10) в уравнение (9) и выразив угол поворота ротора, окончательно получим:

₌ (М-М^-Дф^-гфД

Значение электромагнитного момента М можно получить через интегрирование тензора натяжения Максвелла (Maxwell stress tensor) [6]. Опуская математические выкладки, приведем формулу к конечному виду:

M = ^rlkABnB,dS,

1 9²A_{mk ।} 1 d²A_{mk : o}, PoH &² HoH 9y²

где D_r - диаметр ротора; /_б - ширина воздушного зазора; B_n, B_t - соответственно нормальная и тангенциальная составляющие вектора магнитной индукции относительно поверхности ротора. Интегрирование ведется по поверхности, окружающей ротор и проходящей через центр воздушного зазора.

Значения проекций вектора магнитной индукции на оси координат находятся из выражений, которые следуют из определения векторного магнитного потенциала (4) и условия плоскопарал-лельности поля:

ду у дх

В соответствии с (8), (11), (12)и(13) был разработан алгоритм, реализующий конечноэлементную математическую модель асинхронного двигателя с короткозамкнутым ротором. Следует отдельно подчеркнуть, что при разработке модели были использованы следующие упрощения и допущения:

• •    магнитное поле в пределах активного пространства машины является плоскопараллельным;

• •    зависимость между индукцией и напряженностью магнитного поля является линейной;

• •    магнитопровод машины обладает бесконечным сопротивлением, то есть вихревые токи в стали отсутствуют;

• •    соединительные кольца «беличьего колеса» ротора обладают нулевым сопротивлением.

На рис. 2 представлены расчетные кривые переходных процессов пуска АД при обрыве одного стержня ротора. Расчеты проводились на основе использования геометрических параметров и данных электродвигателя АО2-42-4. В ходе исследований было установлено, что кривые, приведенные на рис. 2 практически не отличаются от аналогич-

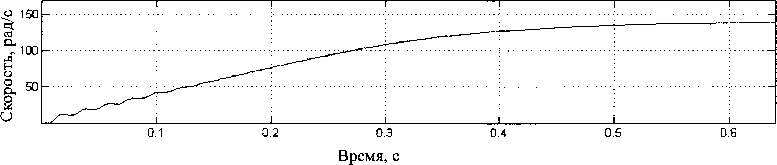
Рис. 2. Расчетные кривые переходных процессов пуска АД при обрыве стержня ротора

ных кривых, полученных при прочих одинаковых условиях для исправного двигателя. Однако в картине магнитного поля поперечного сечения машины во время пуска были выявлены периодически возникающие искажения в области сломанного стержня ротора. Эти искажения оказывают влияние на форму статорного тока. На рис. 3 показана рассчитанная с помощью модели мгновенная кар- тина магнитного поля исправного двигателя (рис. 3, а) и картина поля, характерная для обрыва стержня ротора АД (рис. 3,6).

Поскольку вследствие симметричности асинхронного двигателя любая неисправность одинаково влияет на токи во всех статорных обмотках, то для проведения диагностики достаточно иметь осциллограммы только одного фазного тока. На рис. 4 представлены расчетные кривые пусковых статорных токов фазы А для исправного двигателя (рис. 4, а) и двигателя с одним сломанным стержнем ротора (рис. 4, б).

Незначительное отличие кривых свидетельствует о том, что амплитуда дополнительных составляющих тока статора, обусловленных обрывом стержня ротора, много меньше общего статорного тока. Для проведения анализа из сигнала предлагается удалить основную составляющую тока, соответствующую частоте первой гармоники питающего напряжения. Для этого аппроксимируем ее в виде синусоиды, модулированной в общем случае по амплитуде, частоте и фазе [7]:

4X0=^(0sin(M(0+5(?)).                   (14)

Для нахождения зависимостей Л(/), ы(?) и 8(f) предлагается воспользоваться алгоритмом обра-

а)                                                   б)

Рис. 3. Мгновенная картина магнитного поля в поперечном сечении: а) исправный АД, б) АД со сломанным стержнем ротора

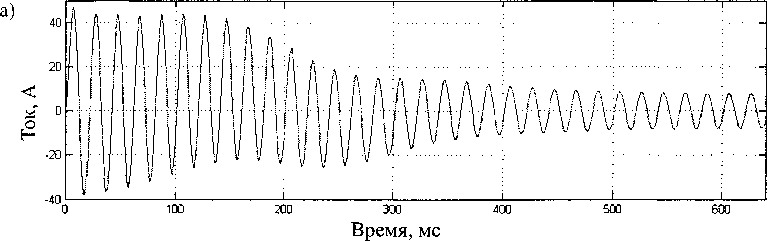
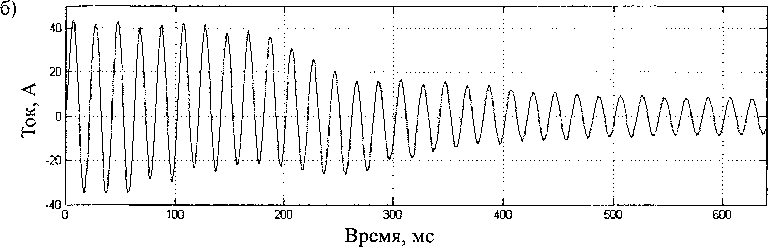
Рис. 4. Пусковой ток статора (фаза А): а) исправный двигатель; б) обрыв стержня ротора

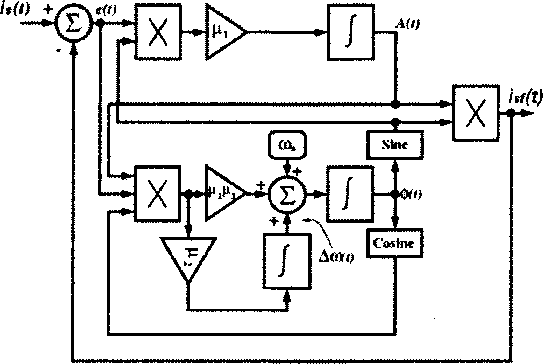
Рис. 5. Алгоритм для выделения из сигнала тока основной составляющей

ботки сигналов, описанным в [7]. Блок-схема алгоритма представлена на рис. 5. На вход системы обработки сигналов поступает информация о статорном токе 4(0- После соответствующих преобразований на выходе промежуточного блока формируется основная составляющая статорного тока 4/0, соответствующая частоте первой гармоники питающей сети двигателя. Если её удалить из статорного тока, то удается получить остаточный ток, характеризующий отклонение формы тока статора от синусоидальной.

После удаления из статорного тока на рис. 5 основной составляющей можно получить кривые остаточного тока, приведенные на рис. 6. Откуда видно, что обрыв стержня ротора приводит к появлению пиков в остаточном токе и, следователь но, к локализованной во времени несинусоидаль-ности формы пускового тока.

Для анализа формы остаточного тока статора предлагается использовать вейвлетные преобразования [8, 9], особенно эффективные при наличии в сигнале помех и высших гармоник сети. На рис. 7 представлены коэффициенты вейвлет-преобразо-вания (вейвлетные спектры) остаточного тока статора, приведенного на рис. 6.

Всплески вейвлет-коэффициентов на втором спектре (рис. 7, б) соответствуют пикам остаточного тока. Данный метод может быть положен в основу диагностики повреждений ротора по осциллограмме пускового тока двигателя.

Предлагаемая методика компьютерных исследований на основе моделей, позволяющих реа-

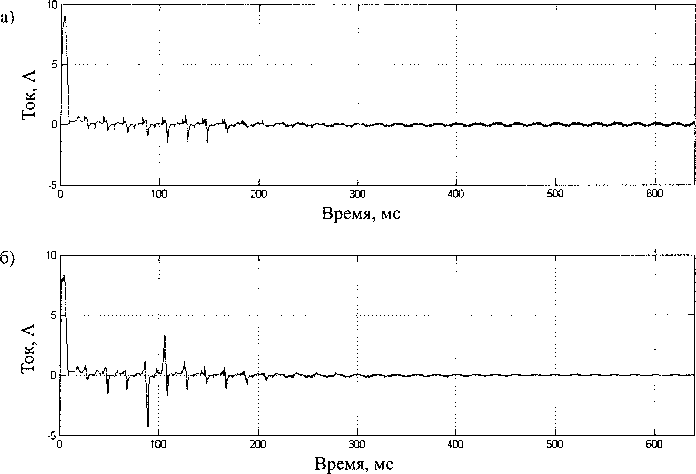
Рис. 6. Остаточный пусковой ток: а) исправный двигатель, 6) обрыв стержня ротора

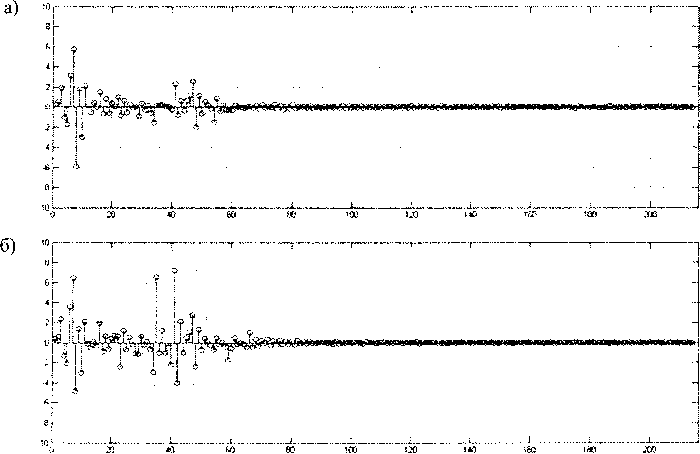
Рис. 7. Коэффициенты вейвлет-преобразования остаточного тока статора

лизовать в своем составе различные неисправности, дает возможность создать в конечном итоге библиотеку вейвлетных спектров по каждому виду неисправностей, определяемых в динамических режимах, и создать на этой основе современные компьютеризированные системы диагностирования электродвигателей