Разработка методов формирования цвето-текстурных признаков для анализа биомедицинских изображений

Одним из важнейших диагностических методов, который до сих пор выполняется вручную лаборантами, остается общеклиническое исследование крови. Именно данный анализ крови тонко отражает реакцию кроветворных органов на воздействие на организм различных физиологических и патологических факторов [1]. Важным диагностическим показателем является количество и процентное соотношение каждого из типов лейкоцитов (лейкоцитарная формула). Лейкоциты различны по внешнему виду и функциям. Различают следующие виды лейкоцитов: нейтрофилы (палочко-ядерные, сегментноядерные), эозинофилы, базофилы, моноциты, лимфоциты [2].

Широкое распространение, трудоемкость выполнения и низкое качество результатов при ручном анализе делает автоматизацию общеклинического анализа крови необходимой и актуальной задачей. Рассмотрим принцип работы системы автоматической диагностики. Изображение препарата крови формируется подключенной к окуляру микроскопа фотокамерой. Оно представляет собой фон, с относительно постоянной яркостью, на котором присутствуют различные форменные элементы (клетки крови). Затем на изображении выделяются лейкоциты, которые представляют собой связные области. Для каждого лейкоцита определяется его тип. И подсчитывается общее количество клеток каждого типа.

Целью работы является разработка признаков для классификации изображений лейкоцитов. Рассматриваются классы: эозинофилы, базофилы, моноциты, лимфоциты.

лейкоцитов. Подход, основанный на матрицах вероятностного распределения (МВР) яркости, уже не раз очень успешно использовался для выделения аналогичной информации [4, 5, 6].

К недостаткам методов МВР можно отнести: работу с полутоновыми изображениями; использование целочисленного формата данных; высокую вычислительную сложность, заключающейся в необходимости работы с трёхмерными матрицами распределения вероятности. В данной работе рассматривается модификация существующих методов для устранения указанных недостатков.

1.    Метод цвето-текстурного анализа

Текстурные признаки – это статистические характеристики многомерного вероятностного распределения интенсивности отсчетов цветовых компонент.

Будем рассмотривать цветное изображение в формате RGB, которое представляется отсчетами функции интенсивности цветовых компонент f ( m, n ) = ( f_R ( m , n ) f c ( m , n ) f_B ( m , n ) ) T , где m, n ^e Z . Как известно в пространстве RGB присутствует кросс-канальная корреляция, что приводит к статистической зависимости признаков, вычисленных по разным цветовым каналам. Поэтому необходимо использовать декоррелированное цветовое пространство. Таким является цветовое пространство Ruderman l a в [7], которое получено на основе анализа главных компонент в пространстве LMS [7].

Переход в цветовое пространство l a в из RGB осуществляется в два этапа.

1) Переход из RGB в LMS [7]:

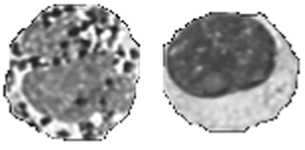
Рис. 1. Изображения лейкоцитов

В качестве основы для исследований был выбран метод, предложенный Хараликом в [3], называемый в дальнейшем статистическим текстурным анализом. Задачей является выделение признаков, связанных с локальными текстурными особенностями

' L '

M

I ^ )

' 0,3811

0,1967

( 0,0241

0,5783

0,7244

0,1288

0,0402Y R )

0,0⁷⁸² G

0,8444 J^ B J

2) Переход из LMS в l ap [7]:

< l )

a

IpJ

" 0,5774 0,4082 ( 0,7071

0,5774

0,4082

- 0,7071

0,5774 )

- 0,8164

0 )

' lg LM' l^g M I lg S )

Здесь цветовые компоненты RGB нормированы так, чтобы принимать значения в диапазоне [ 0;1 ] .

Для того, чтобы достичь инвариантность к цвету, необходимо привести статистические характеристики каждой компоненты к заранее определенным величинам, например, m = 0; о = 1. Это можно сделать, выполнив для каждого канала поэлементную обработку следующего вида:

Пусть каждому из случаев соответствуют функции распределения f 1² ( x , y , z ) , F ₂ ² ( x , y , z ) , F ₂ 3 ( x , y , z ) , F ₂ 4 ( x , y , z ) .

В результате усреднения получим функцию распределения:

‘ _ l - ml

¹ о ;

'

a

a-ma o. _ p-me Z« ; e =        , о         о

где m - математическое ожидание, о - дисперсия.

В данной работе рассматриваются статистические методы формирования признаков, основанные на 3-х мерной функции распределения вероятности яркости в 3-х соседних точках.

Рассмотрим интенсивности заданного цветового канала С (одного из l ap ) в трех точках, находящихся на заданном расстоянии друг от друга:

M ₀ = f_c ( m , n ) , M 1 = f ( m + A m_pn + A n_x),

M ₂ = f c ( m + A m ₂, n + A n ₂).

Обозначим p ( m 0 = x , m 1 = y , m ₂ = z ) - вероятность появления точек с яркостями x , y , z . Тогда

F ( x , y , z ) = 4 ( f² ( x , y , z ) + F ² ( x, y , z ) +

+ F 3 ² ( x, y , z ) + F ² ( x , y , z ) ) .

Введем следующие числовые характеристики: Корреляция:

R = J xyzdF ( x , y , z ) .

R ³

Затенение:

S = J ( x + y + z ) dF ( x , y , z ) .

R ³

Контраст:

x - z | + | y - z I) dF ( x , y , z ) ,

Рис. 2. Примеры взаимного расположения точек

Так как нет необходимости учитывать порядок расположения соседних отсчетов, перейдем к следующей функции распределения, усреднением по следующей схеме:

³ R³

K 2 = J| ( ^{x -} y )( ^{x - z} )( y ^{- z} )| ^{dF (} x y , ^z ) .

R ³

Инерция:

I 1 = ¹ J ( ^{( x -} y ^{) 2 +( x}

3 _R 3

^^^^^в

z ) ² + ( y - z ) ² ) dF ( x , y , z ) ,

I 2 = J ( ^{x -} y ) ² ( ^{x - z} ) ² ( y ^{- z} ) ^{2 dF ( x} , y , ^z ), R³

Признаки записаны для нулевого математиче-го ожидания. Общий вид признака, можно пред

F^г ( x , y , z ) = 6 ( F ¹ ( x , y , z ) + F ¹ ( x , z , y ) +

+ F ¹ ( y , x , z ) + F ¹ ( y , z , x ) +

ставить как:

C = J g ( x, y , z ) dF ( x, y , z ) .

R ³

В случае, если исходная функция распределения не известна, можно использовать эмпирическую функцию распределения вероятности [8]: ^F ( x . y . z ) = Ng. где k - количество элементов выборки, попадающих в область x <  x , y ' <  y ,

+ F ¹ ( z , x , y ) + F ¹ ( z , y , x ) ) .

Для обеспечения инвариантности, относительно поворота на угол кратный 45 ° . Будем рассматривать следующие расположения точек:

• 1.    A m _; = A k 1 ; A n _; = A 1 1 ; A m ₂ = A k ₂; A n ₂ = A 1 ₂,

• 2.    A m _; = A 1 1 ; A n _; = A k 1 ; A m ₂ = A 1 ₂; A n ₂ = A k ₂,

• 3.    A m _; = A 1 1 ; A n _; = A k 1 ; A m ₂ = -A 1 ₂; A n ₂ = A k ₂,

• 4.    A m _; = -A k 1 ; A n _; = A 1 1 ; A m ₂ = -A k ₂; A n ₂ = A 1 ₂.

z <  z . Тогда получим следующую выборочную оценку:

1 N - 1

=    E g ⁽ x, y- z ).

N i = 0

Значение признаков вычисляется для каждой цветовой компоненты, поэтому далее будем использовать обозначения, включающие название цветового канала и признака, например: l Shading ( lS ) – затенение, рассчитанное по компоненте l .

Таким образом, процедура вычисления признаков заключается в одном проходе по изображению заданными шаблонами взаимного расположения то-

чек. Экспериментальные исследования на натурных изображениях показали, что предложенный метод вычисления признаков является более быстрым и требует меньше памяти по сравнению с методом, основанным на вычислении 3-х мерной матрицы вероятностного распределения (гистограммы).

2.    Дискриминантный анализ признаков

Для определения степени эффективности признаков при классификации используются элементы дискриминантного анализа [9, 10]. Цель выбора признаков состоит в выделении признаков, которые являются наиболее эффективными с точки зрения разделимости классов. Разделимость классов зависит только от распределения объектов в классах, а также от используемого классификатора.

В дискриминантном анализе критерий разделимости записывают с использованием матриц рассеяния внутри классов и матриц рассеяния между классами. Пусть S_w , – матрица рассеяния внутри классов, S_b – матрица рассеяния между классами, S_m – матрица рассеяния смеси. Для выбора признаков рассматривались три критерия:

• J ₁ =tr S_m /tr S_w ,

• J 2 =| S m |/| S w |,

• J 3 = tr( S w ^{- 1} S b ) .

Наилучшие признаки те, для которых критерий разделимости максимален [9, 10]. В данной работе рассматривалась задача выбора трёх признаков. Из всего множества векторов признаков, построенных по обучающей выборке, вычислялись критерии разделимости по всем тройкам, количество которых равно C ₁ ³ ₈ = 816 . В таблицах 1-3 показаны результаты вычисления критериев разделимости.

Из таблиц видно, что критерии J ₁ и J ₃ дали одинаковые результаты, при этом наилучшими оказались признаки: l Shading ( lS ), a Contrast2 (α K ₂ ), b Shading ( β S ) – 1-ый набор. А по критерию J ₂ лучшими признаками являются: l Shading ( lS ), a Contrast2 ( α K ₂ ), b Correlation ( β R ) – 2-ой набор. Расположения объектов в пространстве признаков данных наборов показано на рисунках 2, 3, из которых видно, что обрабатываемые четыре класса лейкоцитов линейно разделимы.

Можно заметить, что полученные наборы признаков отличаются одним признаком (признак β S и β R ). Вследствие этого, в дальнейшем для построения классификатора планируется использовать четыре признака, максимизирующие выбранные критерии разделимости классов.

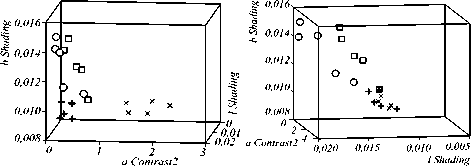
Рис. 3. Расположение объектов в пространстве 1

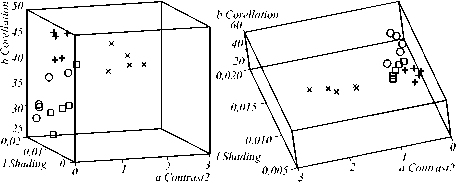
Рис. 4. Расположение объектов в пространстве 2

Таблица 1. Значения критерия 1

lS	α K 2	β S	10,66213
α S	α K 2	β S	10,66211
α R	α S	β S	2,08106

Таблица 2. Значения критерия 2

lS	α K 2	β R	163,95
lS	α K 2	β S	159,86
lK 2	lI 2	α R	3,38

Таблица 3. Значения критерия 3

lS	α K 2	β S	17,09
lI 1	α S	α K 2	17,01
lK 2	lI 2	α R	1,80

Заключение

В работе предложен метод вычисления цветотекстурных признаков, основанный на вычислении статистических характеристик двумерных случайных полей. Экспериментальные исследования проводились на натурных изображениях клеток крови. Работа алгоритма сравнивалась с уже реализованными алгоритмами на основе МВР. В результате сделаны следующие выводы:

• 1.    Полученные признаки позволяют проводить автоматическую классификацию клеток крови.

• 2.    Алгоритм обладает высокой скоростью, в сравнении с методами, основанными на анализе матрицы вероятности [5, 6].

Анализ проведенных экспериментальных исследований свидетельствует о том, что разработанные алгоритмы могут применяться для системы диагностики заболеваний крови. Одним из достоинств работы можно назвать сокращение затрат времени на обработку изображения.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE) и программы Президиума РАН «Фундаментальные науки – медицине», гранта РФФИ № 06-07-08006-офи, гранта РФФИ № 07-08-96611.