Разработка методов и программных средств подавления шумов в интерферограммах на этапе их предварительной обработки

В настоящее время в задачах неразрушающего контроля все шире используются методы, основанные на оптической и электронной интерферометрии [1]. При этом для автоматизации контроля, увеличения скорости и точности получения результатов интерферограмма регистрируется ПЗС-матрицей и затем обрабатывается на компьютере [2]. Однако искажения интерферограммы, обусловленные различного рода шумами, часть из которых является практически неустранимыми на аппаратном уровне, существенно снижают точность восстановления фазы интерференционных полос и, вследствие этого, дают неверное представление об исследуемом объекте.

Для увеличения качества проводимого контроля предлагаются различные компьютеризированные методы предварительной обработки интерферограмм, направленные на существенное снижение или даже удаление шумов из зарегистрированной интерференционной картины без потери полезной информации об исследуемом объекте [3-7]. Настоящая работа посвящена анализу и модернизации таких методов с целью уменьшения нежелательного искажения функции деформации волнового фронта, возникающих при их использовании. Рассмотрено применение методов предварительной обработки интерферограмм для устранения определенных типов их шумового загрязнения и проведено сравнение эффективности различных методов, устраняющих одинаковый тип такого загрязнения. Описан алгоритм, позволяющий осуществить комплексную очистку интерферограммы от всех основных типов шумов и помех.

Модель распределения освещенности на интерферограмме

Анализ причин возникновения шумов и помех на интерференционных картинах позволяет выделить ряд условий их возникновения, зависящих как от использованной схемы интерферометра и многоэлементного фотоприемника, так и от свойств окружающей среды. Эти шумы и помехи вызваны разными факторами, имеют различную структуру и, в силу этого, практически невозможно создать метод, позволяющий одновременно и полностью очистить от них интерферограмму.

Общий случай распределения освещенности на зашумленной интерферограмме можно описать уравнением [8]

I (X, y ) = M (X, y){c (X, y) +

+ A cos [to x X + to у У + ф ( x , y ) ] } + B ( X , У ) , (1) где M ( x, y ) - мультипликативный шум; C ( x, y ) - аддитивный шум; A - амплитуда синусоиды, соответствующая максимально возможной для передачи ПЗС матрицей видеокамеры яркости изображения; ю x и to _y - составляющие пространственной частоты интерференционной картины; ф ( x, y ) - составляющая разности фаз интерферирующих волн, вызванная деформацией фронта волны под воздействием исследуемого образца; B ( x, y ) - белый шум.

Модель распределения освещенности, представленная в виде уравнения (1), позволяет создать алгоритм комплексного подавления шумов на интерферограмме как группу методов, выполняющихся в строгой последовательности и очищающих интерференционную картину послойно. На первом этапе подавляется белый шум. На втором этапе производится выравнивание контраста изображения, приводящее к подавлению таких составляющих мультипликативного и аддитивного шумов которые искажают значительную область интерференционной картины, оказывая влияние одновременно на несколько интерференционных полос.

К шумовому загрязнению, которое может быть представлено в виде составляющих мультипликативного и аддитивного шума, относятся блики (рис. 1). Они, по сравнению с общей картиной шумового загрязнения, имеют более простую пространственную структуру и могут быть аппроксимированы поверхностью невысокого порядка. Это обусловлено тем, что блики имеют единственный максимум яркости, постепенно убывающей к краям влияния блика.

На третьем, заключительном этапе, должен быть подавлен высокочастотный аддитивный шум, который может включать паразитные интерференционные картины, следы дифракции лазерного излучения на пылинках и т.д.

-M/vw

Рис. 1. Срез распределения освещенности на интерферограмме с неравномерным контрастом, обусловленным бликом, имеющим аддитивную (а) и мультипликативную (б) составляющую шумового загрязнения

Подавление белого шума

Основными причинами возникновения белого шума являются ошибки восприятия сигнала видеокамерой или при его передаче в компьютер. Наличие белого шума приводит к искажению значения освещенности в точках интерферограммы с некоторой вероятностью (рис. 2).

Рис. 2. Интерферограмма с полезным сигналом, искаженным белым шумом (а), и распределение освещенности на интерферограмме вдоль ее вертикальной оси (б)

Наиболее удобным методом подавления белого шума является метод скользящей средней, который в общем случае используется для сглаживания изображений [9]. Однако при его использовании применительно к обработке интерферограмм наряду с подавлением белого шума снижается контраст интерференционных полос и происходит их смещение в плоскости интерферограммы. Для исправления указанных недостатков предложено вычислять но- вое значение освещенности лишь для тех точек, в которых собственное значение освещенности искажено белым шумом. Они определяются из условия того, что модуль разности освещенности исследуемой точки и освещенности каждой из восьми соседних точек больше некоторой величины е, которая, в зависимости от уровня помех, выбирается в районе четырех процентов от максимального уровня сигнала, воспринимаемого ПЗС-матрицей. При этом новая величина освещенности зашумленной точки рассчитывается по формуле

N

I ( x , У ) = Т7 Z fk (0) (2) N к = 1

Здесь N – число направлений, по которым строятся аппроксимирующие функции вида f_k ( t ) = a_kt ² + b_kt + c_k . Параметры a_k , b_k , c_k находятся методом наименьших квадратов от точек fk ^{( - 2}X fk (—D, fk ⁽¹⁾, fk ⁽²⁾ равных при N =4 для ^каждой из функций, соответственно, I ( x - 2, у - 2 ) , I ( x - 1, У - 1 ) , I ( x + 1, У + 1 ) , I ( x + 2, У + 2 ) , I ( x - 2, У ) , I ( x - 1, У ) , I ( x + 1, У ) , I ( x + 2, у ) , I ( x , У - 2 ) , I ( x , У - 1 ) , I ( x , У + 1 ) , I ( x , У + 2 ) и I ( x ^- 2, ^У + ² ) , I ( x ^- 1, ^У + 1 ) , I ( x + 1, ^{У -} 1 ) , I ( x + 2, у - 2 ) .

Как показывает практика обработки интерферограмм, предложенные изменения позволяют наиболее точно определить величину освещенности для точек максимума и минимума интерференционных полос, что почти не приводит к возникновению ошибки при определении функции деформации волнового фронта.

Выравнивание контраста изображения

Выравнивание контраста освещенности на интерферограмме, искаженной бликами, предлагается осуществлять методом искусственной привязки экстремумов к заданному уровню [10]. Для реализации метода определяются координаты точек глобальных экстремумов функции распределения освещенности интерференционной картины. Далее, по точкам, определяющим глобальные минимумы освещенности методом наименьших квадратов, находится аналитический вид функции I min ( x , у ) , представляющей собой поверхность невысокого (второго либо третьего) порядка в зависимости от сложности формы удаляемого блика. Новое распределение освещенности рассчитывается по формуле

• I ' ( x , У ) = I ( x , У )^- I min ( x , У ) (3) где I ( x , у ) - исходное распределение освещенности.

Аналогичным образом по найденным точкам глобальных максимумов определяется аналитический вид функции I max ( x , у ) , и распределение освещенности с выровненным контрастом определяется по формуле:

I "( % , y ) = A ^{1 1} x. ^, y ) (4) I max ( ^x , У )

где A – максимально возможный размах значений функции освещенности.

Если интерферограмма искажена мультипликативным шумом более сложного вида, то для выравнивания контраста целесообразно использовать метод, суть которого заключается в последовательной коррекции интерферограммы шаблоном, представляющим собой промежуточный массив данных, полученных из Фурье-образа некой двумерной функции, имеющей спектр, подобный спектру блика [11]. В качестве такой функции удобно выбрать двумерную функцию (купол) Гаусса, Фурье-образ которой в низкочастотной области отвечает за величину блика, а в высокочастотной области описывает его резкие края.

Полный алгоритм выравнивания контраста интерферограммы выглядит следующим образом. В соответствии с формулой

J 1

F ( x , У ) = exp 5- 2

^{( x -} c x ⁾² + ⁽ x - c y ⁾²

где c_x , c_y и a _x , a _y - координаты центра и параметры ширины купола вдоль осей x и y , соответственно, формируется картина распределения яркости, соответствующая куполу Гаусса.

Затем вычисляются Фурье-преобразования от полученной картины и исходной интерферограммы, и определяется новый Фурье-образ интерферограммы, как результат комплексного перемножения соответствующих элементов полученных спектров пространственных частот.

Восстановленная из Фурье-образа интерферограмма будет отличаться от исходной тем, что у нее будут значительно ослаблены все высокочастотные компоненты. Что же касается низкочастотных спектральных компонент, отвечающих за формирование блика, то они останутся почти без изменения.

Из формулы (5) видно, что параметрами, отвечающими за уровень ослабления спектральных компонент, являются a _x и a _y . При этом координаты центра купола c_x и c_y должны соответствовать центру устраняемого блика.

Очевидно, что чем больше величины a _x и a _y , тем сильнее ослабляются спектральные компоненты, соответствующие высоким частотам Фурье-спектра интерферограммы, и тем на больший диаметр устраняемого блика рассчитана такая фильтрация.

Далее, поделив каждый элемент (величину яркости точки) исходной интерферограммы на соответствующий элемент восстановленного из Фурье-образа изображения, мы получим итоговую интерферограмму с выровненным контрастом. Для подобного преобразования яркость каждой точки изображения должна быть представлена в виде дробного числа, принадлежащего диапазону [-1;1].

В результате применения данного метода выравнивания контраста изображения каждый элемент (величина яркости точки) исходной интерферограммы делится на вычисленный уровень фоновой яркости, созданной бликом, в этой точке, что кроме устранения блика ведет к общему снижению контраста изображения. Это требует последующей обработки интерферограммы линейным методом увеличения контраста.

Рисунок 3 иллюстрирует возможности выше описанных методов выравнивания контраста интерференционной картины.

Подавление высокочастотного аддитивного шума

Высокочастотный аддитивный шум, как уже отмечалось выше, представляет собой паразитные интерференционные картины и по своей структуре сходен с основной интерференционной картиной, но лежит, как правило, в более высокочастотной области. Поэтому его подавление удобно осуществлять с помощью частотной фильтрации, в частности, осуществляемой методами Фурье-преобразования.

При использовании метода каждая точка исходной картины распределения освещенности в интерферограмме представляется как сумма N 2 синусоид:

N /2 - 1    ,----------------------

I (x )= X 2 V Fr (p) + Fm (p)

p = 0

J 2n x cos < — px + arctg

I N

F m ( P )

_ F r ( P ) JJ’

где N – количество точек в отсчете, по которому производится обработка; F_r и F_m – действительная и мнимая части массива комплексных чисел, являющегося результатом прямого преобразования Фурье.

Очевидно, что часть из этих синусоид будет отвечать за полезную информацию, а часть за шумы. Таким образом, используя представление данных, в виде выражения (6), подавление аддитивных шумов с помощью амплитудной Фурье-фильтрации можно осуществлять в три этапа [12,13]:

• -    по Фурье-спектру зашумленной интерферограммы определяются те пространственные частоты, которые несут полезную информацию, т.е. синусоиды этих частот имеют наибольшую амплитуду;

• -    на основе интенсивности полезного сигнала вычисляется «уровень шума»;

• -    все спектральные компоненты с интенсивностью сигнала меньшей установленного порогового значения приравниваются к нулю.

После такой обработки исходная интерференционная картина складывается не из всех N 2 синусоидов, а лишь из 5-20, имеющих наибольшую амплитуду. Обычно уровень шума вычисляется как 10% от уровня полезного сигнала, но в зависимости от вида обрабатываемой интерферограммы это значение может меняться.

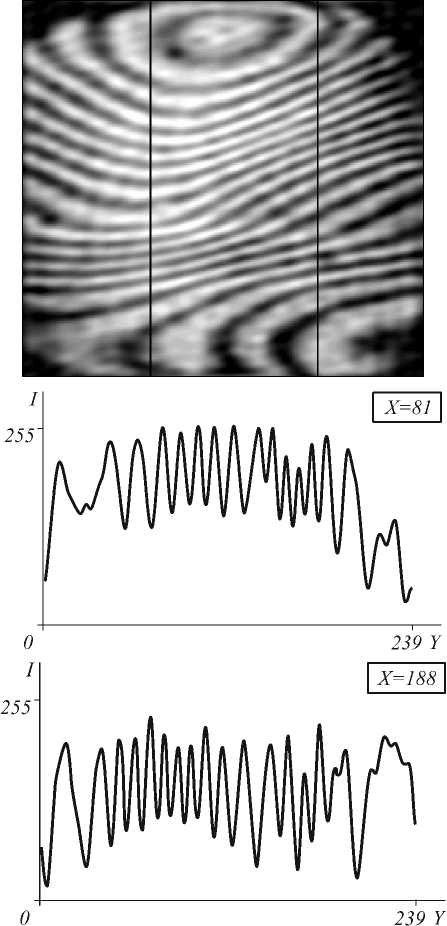
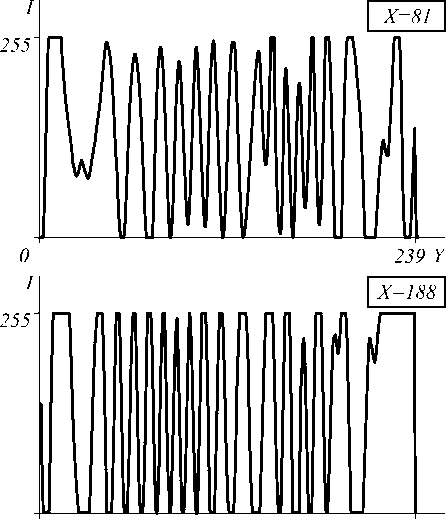
Рис. 3. Интерферограмма до (а) и после (б) обработки методом выравнивания контраста; профиль исходной (в) и обработанной (г) интерферограммы

С помощью амплитудной Фурье-фильтрации довольно надежно отсеивается аддитивный шум, вызванный дифракцией лазерного излучения на пыли и других микрочастицах. На рис. 4 показан результат обработки реальной интерференционной картины методом амплитудной Фурье-фильтрации.

Заключение

В статье предложен метод комплексной предварительной обработки интерферограмм, проводящийся в три этапа. В ходе обработки интерференционной картины в зависимости от присутствующих на ней шумов и помех могут выполняться не все из предложенных этапов, но порядок обработки сохраняется. Все методы модернизированы таким образом, чтобы в ходе обработки практически не оказывать влияния на функцию деформации волнового фронта и разность фаз интерферирующих волн, максимально сохраняя информацию об исследуемом образце.

Разработаны алгоритмы автоматического подбора начальных параметров для предложенных методов шумоподавления в зависимости от вида интерферограммы.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ и американского фонда гражданских исследований и развития (CRDF грант № Y1-P-14-03) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), а также при поддержке гранта Президента РФ № НШ-1007.2003.01.