Разработка модели аэротермодинамики атмосферы для исследования процессов пыления на хвостохранилищах с использованием программы COMSOL

*Институт проблем промышленной экологии Севера КНЦ РАН, г. Апатиты, Мурманская обл., Россия; e-mail: , ORCID:

*Institute of North Industrial Ecology Problems KSC RAS, Apatity, Murmansk region, Russia; e-mail: , ORCID:

Компьютерное моделирование на базе верифицированных программ (FLOWVISION, ANSYS FLUENT, ANSYS CFX, COMSOL и др.) используется для решения задач на объектах рудничной аэрологии (карьеры, подземные выработки) и горнопромышленных предприятиях, оказывающих негативное воздействие на окружающую среду (хвостохранилища). Повышение интереса к компьютерному моделированию обусловлено созданием высокопроизводительных компьютеров, разработкой верифицированных программных комплексов вычислительной гидродинамики (CFD-моделирование), а также подготовкой поколения специалистов в области информационных технологий.

Обзор программных продуктов, используемых в оценке качества атмосферы

Специализированные и собственные программы. В настоящее время известно большое количество специализированных CFD-моделей аэротермодинамики и переноса загрязнений в атмосфере. Например, на сайте Университета в г. Гамбурге содержится актуальная (май 2022 г.) база данных (более сотни) программных продуктов¹, разработанная в рамках проекта COST728 "Enhancing Meso-scale Meteorological Modelling Capabilities for Air Pollution and Dispersion Applications". Авторы проекта классифицировали эти программы как по пространственному масштабу, так и по областям приложения кодов.

В силу недоступности и сложности в применении профессиональных программных продуктов, ограниченности финансовых средств часто приходится применять доступные ресурсы; сделать это можно либо посредством разработки собственных программ, либо при использовании неспециализированных (коммерческих) программных кодов, настраивая их под конкретные задачи.

Многие исследовательские группы настроены на разработку собственных компьютерных программ и моделей, например:

• –    группа ученых Тульского государственного университета под руководством Качурина Н. М. изучали процессы переноса загрязнений на объектах горной промышленности на базе численного моделирования ( Качурин и др., 2016 );

• –    сотрудники Института динамики геосфер им. М. А. Садовского РАН (Хазинс В. М. с коллегами) разработали эйлерову модель, предназначенную для моделирования начальной стадии образования и подъема пылевого облака ( Khazis et al., 2020 );

• –    томские специалисты (Нутерман Р. Б., Старченко А. В. и др.) выполнили значительный объем исследований по разработке математической модели аэродинамики и переноса примеси от выбросов автотранспорта в элементах городской застройки, изучали структуры течений над взлетно-посадочной полосой аэропорта и др. ( Nuterman et al., 2010; Старченко и др., 2015 );

• –    сотрудники факультета геофизики чилийского университета г. Сантьяго ( Flores et al., 2014 ) изучали проблему циркуляции воздуха внутри крупных карьеров при интенсивной инсоляции, в которых преобладают механические и плавучие эффекты (имеющие решающее значение при изучении рассеивания загрязняющих веществ внутри и снаружи карьера) с использованием ранее разработанного решателя OpenFOAM.

Неспециализированные (коммерческие) программные продукты. Группы специалистов в области охраны окружающей среды (прежде всего атмосферы) и аэрологии карьеров, а также преподаватели и сотрудники вузов технического профиля в своей деятельности пытаются использовать CFD-модели, разработанные на базе неспециализированных программных кодов.

Ниже представлена собранная и проанализированная информация по примерам использования неспециализированных программ (FLOWVISION, ANSYS FLUENT, COMSOL и др.) при решении проблем оценки качества воздуха на объектах горнопромышленного комплекса (карьеры, хвостохранилища, отвалы) как в России, так и за рубежом. Ссылки на публикации, не приведенные в этом обзоре, можно найти в библиографических списках, указанных в работах упомянутых авторов.

FLOWVISION2

Для оптимизации формирования отвалов Башировым Н. Р. ( Баширов, 2018 ) произведена компьютерная симуляция движения воздуха при разной геометрии прикарьерного пространства и различных температурах воздуха. Автором поставлена цель – обеспечить концентрацию и направление движения воздушного потока непосредственно в чашу карьера в условиях естественного проветривания путем формирования контуров отвалов.

В работах сотрудников Санкт-Петербургского горного университета (Гридина Е. Б., Петров И. А., Черкай З. Н.) (Гридина и др., 2017b) отмечается, что наиболее сложным элементом моделирования процесса проветривания карьерного пространства является температурная стратификация атмосферы карьера и учет температурных процессов. Анализ структуры ветровых потоков был выполнен на примере модели Оленегорского карьера (Кольский полуостров).

Авторы публикации ( Гридина и др., 2017a ) для моделирования естественного проветривания Оленегорского карьера и изучения распространения вредных примесей в карьерном пространстве использовали низкорейнольдсовую ( k – ε )-модель турбулентности. На начальном этапе моделирования получена структура ветровых потоков в нижней части Оленегорского карьера. На следующем этапе рассмотрена подача отработанного воздуха из подземного рудника через порталы штолен в карьерное пространство.

ANSYS FLUENT3

В работе ( Ястребова, 2014 ) построена модель процесса распространения воздушных потоков, которая позволяет изучить зависимость количества застойных зон от горнотехнических и климатических параметров с целью нормализации атмосферы карьера. В ходе исследований Ястребовой К. Н. установлено, что рост скорости ветра на площадках в карьере возрастает по мере увеличения расстояния от откоса уступа.

Сотрудниками Санкт-Петербургского горного университета Гендлером С. Г. и Борисовским И. А. выполнен цикл исследований ( Гендлер и др., 2021 ):

• 1)    осуществлено математическое моделирование аэродинамических процессов при естественной вентиляции, а также комплексной вентиляции, включающей принудительную подачу воздуха в карьерное пространство по системе выработок, и установлено, что образование зон рециркуляции характерно для третьей стадии разработки, причем ее максимальный объем приурочен к завершающему этапу работ;

• 2)    исследована аэродинамика процессов при естественном проветривании золоторудных карьеров на различных этапах отработки месторождения; решена задача по оценке эффективности естественной вентиляции на различных этапах разработки месторождения с учетом повышения глубины горных работ;

• 3)    изучено влияние температурных инверсий на эффективность проветривания карьерного пространства. Результаты исследований свидетельствуют о том, что область применения естественной вентиляции карьеров, расположенных в Арктической зоне России, следует устанавливать с учетом стохастических законов изменения термодинамических параметров атмосферного воздуха, определяющих величину температурного градиента в воздухе.

Значительный объем исследований выполнен группой сотрудников Горного института КНЦ РАН под руководством Козырева С. А. В работе ( Козырев и др., 2017 ) с использованием 3D-компьютерного моделирования исследован характер распределения воздушных потоков на поверхности и в карьерном пространстве глубоких карьеров с учетом реального рельефа местности и масштаба карьера рудника Железный Ковдорского ГОКа. Выявлено влияние породных отвалов и прибортовых зон карьера на формирование рециркуляционных зон, вихревых течений и степени ослабления воздушных потоков в различных зонах карьера в зависимости от скорости ветра на поверхности.

В работе ( Амосов и др., 2018b ) изложены отдельные моменты авторского опыта создания компьютерной модели аэротермодинамики атмосферы карьера. Авторы полагают, что изложенный материал будет полезен пользователям программы, на базе которой предпринимаются попытки моделировать аэродинамические процессы с учетом теплового фактора не только в замкнутых областях (на что изначально ориентируют разработчики программы), но и в таких открытых системах, как карьеры и хвостохранилища.

Исследования Амосова П. В. с коллегами ( Амосов и др., 2019 ) посвящены сравнительному анализу результатов численного моделирования аэротермодинамики атмосферы карьеров в условиях температурной инверсии (модели несжимаемого идеального газа и несжимаемой жидкости). По результатам анализа показано, что обусловленные тепловым фактором изменения в структуре скоростного поля и значениях компонент скорости окажут существенное влияние на процесс распространения загрязнений (при прочих равных условиях), что отразится и на времени достижения нормативных показателей чистоты атмосферы.

Цель работы Назарчука О. В. ( Назарчук, 2021 ) заключается в изучении закономерностей и связей распределения угарного газа в атмосфере карьера в условиях температурной инверсии и штиля. Геометрия модели учитывает сложную орографию прилегающей к карьеру территории, а также перепад высот на бортах карьера. Для описания аэродинамических процессов использовано приближение несжимаемой жидкости. Для замыкания системы уравнений неразрывности и Навье – Стокса, осредненных по Рейнольдсу, использована Realizable (к — е)-модель турбулентности.

В работе Yuan Wang с коллегами ( Yuan Wang et al., 2021 ) на основе полевых испытаний, численного моделирования и теоретического анализа в глубоком карьере Sunken в качестве показателя степени сложности диффузии пыли выбрано время диффузии от максимальной концентрации пыли после взрывных работ до сниженной концентрации (до уровня ПДК). В ходе моделирования определено, что угол наклона длинной оси, длина длинной оси замкнутого круга, глубина карьера, скорость ветра и направление ветра являются основными факторами, влияющими на диффузию пыли в карьере Sunken.

В исследовании другой группы китайских ученых (Huang Z. с коллегами) ( Huang Z. et al., 2021 ) изучен механизм удаления пыли. Авторами проведено численное моделирование в реальном времени процесса загрязнения взрывной пылью в карьере с использованием теории двухфазного потока "газ – твердое тело" (метод Эйлера – Лагранжа) и механики взрыва.

В 2015 г. Kumar Vaibhav Raj ( Raj, 2017 ) представил свои изыскания на тему моделирования аэродинамики атмосферы карьера в арктических условиях. В работе представлены методы моделирования геометрической модели карьера от двухмерной модели до полного 3D-моделирования. Особое внимание Raj K.V. уделил правильному подбору параметров расчетной сетки. Для изучения проблемы переноса загрязнений использовались модель с усреднением по Рейнольдсу на основе модели Навье – Стокса (RANS), Realizable ( k – ε )-модель и модель, основанная на моделировании больших вихрей (LES). Прогнозируемые показатели в значительной степени отличались, но оставались в пределах одного и того же порядка величины для всех мест, где были доступны измерения параметров загрязнения.

Сотрудники Горного института УрО РАН (Бублик С. А., Семин М. А.) в работе ( Бублик и др., 2022 ) представили результаты математического моделирования тепло- и воздухораспределения в карьерах при естественном проветривании. В двумерной постановке с учетом естественной конвекции и турбулентного движения воздуха (за исключением теплообмена с горным массивом и влияния солнечной радиации) промоделированы несколько температурных режимов.

Специалистами Казанского национального исследовательского технологического университета ( Купцов и др., 2014 ) предложена вычислительная модель горизонтально однородного пограничного слоя атмосферы, учитывающая различные варианты атмосферной устойчивости (нейтральной, устойчивой и неустойчивой стратификации). Для турбулентного замыкания использована ( k – ε )-модель турбулентности с модифицированными константами и дополнительным источниковым членом в уравнении для кинетической энергии турбулентности. Авторы отмечают, что решаемые в программном продукте уравнения не вполне адекватно описывают физику турбулентности в атмосферном пограничном слое.

COMSOL4

В работе Амосова П. В. с коллегами ( Амосов и др., 2015 ) представлены описание математической модели в приближении слабой сжимаемости и результаты численных экспериментов аэротермодинамических процессов в атмосфере карьера. Задача поступления холодного и теплого воздуха в карьер решается в пространстве реального масштаба в двухмерной постановке. Выполнена симуляция аэротермодинамических процессов применительно к карьерам при различных температурных градиентах и вариации скорости воздуха.

В качестве примера практического использования CFD-моделей в рудничной аэрологии в работах сотрудников Горного института КНЦ РАН приведены результаты двухмерного моделирования структуры полей скорости для карьера Центральный-Глубокий КФ АО "Апатит" и карьера Железный Ковдорского ГОКа на Кольском полуострове. Полученные данные свидетельствуют о существенном ослаблении воздушных потоков на дне глубоких карьеров [более значительном, чем для карьеров средней глубины (до 350 м)]. В публикациях ( Козырев и др., 2014; 2015 ) представлены результаты численного моделирования процессов распределения воздушных потоков в карьерном пространстве и нормализации атмосферы карьера путем нагнетательного способа проветривания; рассмотрены варианты поступления воздуха через вентиляционные восстающие и горизонтальные выработки. В ходе анализа отмечены существенные изменения в структуре скоростных потоков в пространстве карьера при использовании альтернативных способов подачи воздуха.

Результаты исследований процессов пыления на хвостохранилище АНОФ-2 на базе численного моделирования в продолжение начатых Баклановым А. А. работ еще в прошлом веке ( Бакланов, 1988; Baklanov et al., 1998 ) опубликованы в монографии ( Амосов и др., 2014 ), ряде статей ( Амосов и др., 2018а; Амосов и др., 2022 ), представлены в материалах конференций разного уровня. Основные выводы приведены в готовящейся к публикации монографии сотрудников Института проблем промышленной экологии Севера КНЦ РАН.

В работе Амосова П. В. ( Амосов, 2022 ) приведены результаты моделирования процессов проветривания карьера при вариации основных параметров модели, в частности:

• –    определен доминирующий фактор, оказывающий влияние на загрязнение атмосферы карьеров. В паре факторов " взрывные работы - ветровой режим " , действующих на процесс естественного проветривания разнонаправлено, доминирующим является ветровой режим;

• –    исследовано влияние местоположения массовых взрывов и начальной высоты подъема пылегазового облака на время проветривания карьера и уровень загрязнения атмосферы верхнего борта карьера вниз по ветровому потоку; выполнен анализ расчетного времени естественного проветривания карьера и динамики загрязнения атмосферы верхнего борта карьера вниз по ветровому потоку при варьировании двух параметров

модели: местоположения массовых взрывов и начальной высоты подъема пылегазового облака при фиксированных значениях начальной концентрации газовой компоненты в облаке и скорости набегающего ветрового потока;

– выполнена оценка влияния местоположения массовых взрывов, начальной высоты подъема пылегазового облака и скорости ветрового потока на верхнем борту карьера на время естественного проветривания карьера и уровень загрязнения атмосферы верхнего борта карьера вниз по ветровому потоку. В ходе анализа показано, что уменьшение высоты подъема пылегазового облака не всегда обеспечивает снижение уровня загрязнения на верхнем борту карьера вниз по потоку.

Обоснование цели исследования

Приведенные выше примеры по использованию неспециализированных программных продуктов при решении проблем обеспечения качества атмосферы, загрязняемой в результате деятельности предприятий горнопромышленного комплекса, рассматривают воздушную среду в ряде известных приближений (приближение несжимаемой жидкости, для неизотермических потоков модели несжимаемого идеального газа, Буссинеска, слабой сжимаемости), весьма далеких от реальной атмосферы.

Представляется необходимым попытаться, используя возможности неспециализированных программных комплексов (не только COMSOL), определить необходимые и реализуемые модификации программ, чтобы можно было применять их для исследований процессов пыления и переноса пылевых загрязнений при различных состояниях (неустойчивых, нейтральных, инверсионных) приземного слоя атмосферы.

В 1990-х гг. популярным было программное обеспечение PHOENICS⁵, с помощью которого предпринимались попытки численного моделирования пограничного слоя атмосферы и переноса загрязнений в сложных орографических условиях. Так, авторы работ ( Baklanov et al., 1997; Baklanov, 2000 ) для численного моделирования аэротермодинамики атмосферы нейтральной устойчивости решали уравнения гидродинамики с учетом сжимаемости. Замыкание полной системы уравнений достигалось с помощью ( к - е )-модели турбулентности с небольшими модификациями.

При этом авторы ( Baklanov et al., 1997; Baklanov, 2000 ) отмечают, что большинство моделей атмосферного пограничного слоя используют систему уравнений гидротермодинамики с гидростатическим приближением в приближении Буссинеска ( Physick, 1988 ) и без включения полностью сжимаемой системы.

Модель микроклимата атмосферы описана в исследованиях 1970–1990-х гг. ( Берлянд, 1975; Бакланов, 1988; Baklanov et al., 1998; Марчук, 1982; Методы …, 1983; Пененко и др., 1985; Нормализация …, 1986; Бакланов и др., 1995 ) и в работах 2000-х гг. ( Шлычков и др., 2005; Леженин и др., 2016; Шлычков, 2005; Рапута и др., 2014 ); она была реализована применительно к задаче пыления Баклановым А. А. и Ригиной О. Ю. ( Бакланов, 1988; Baklanov et al., 1998 ).

В настоящее время представляется достаточно очевидной необходимость совершенствования разработанных компьютерных моделей с учетом состояния атмосферы. Такое усовершенствование можно осуществить, используя в качестве основы модель, описанную в статье Бакланова А. А. и Ригиной О. Ю. ( Baklanov et al., 1998 ).

Описание моделей

Пространственная математическая модель

В работе ( Baklanov et al., 1998 ) применена модель динамики пограничного слоя атмосферы, которая использует гидростатическое приближение (без учета сжимаемости атмосферы) в приближении Буссинеска. Введение потенциальной температуры и функции Экснера для давления позволяет опустить малые члены и линеаризовать нелинейные члены в уравнениях движения. Трехмерная модель динамики атмосферы в локальном масштабе над сложным рельефом, которая базируется на предыдущих работах авторов ( Бакланов, 1988; Нормализация…, 1986 ), записана в следующем виде:

ди,     ди,

—^L + и, —-д t       дXj

1 д P д 1

р дXj   дXj

- :/

.  ^д x j        J

+^ i ’

д T    д T

--+ и. --+ д t      дXj

д и,

J= = °’ дXj

д

Su =--

³    дXj

x-— и ; t -1+ q_z + j_t , д Xj    ’ ^J

(1а), (1б), (1в)

где i , j = 1, 2, 3; §. = ( lu₂ , - lu_x , g в Т ) ; p , p, T - плотность, функция приведенного давления и потенциальной температуры воздуха; t - время; и 1 , и₂, и₃ - компоненты скорости ветра вдоль осей x ₁, x 2 , x ₃ соответственно; S , l - параметры стратификации и Кориолиса; в - коэффициент объемного расширения; v , X - коэффициенты молекулярно-кинематической вязкости и теплопроводности; Q_z – радиационная составляющая притока тепла; J_T - антропогенный источник; и ' и ‘ и и ‘ Т¹ - турбулентные члены, определяемые из модели замыкания.

Предлагается принять приведенную систему уравнений за основу в достижении цели, а именно определить необходимые изменения в системе уравнений, описывающих турбулентный режим движения воздуха в приближении несжимаемой жидкости в неспециализированном программном коде COMSOL, чтобы модифицированную модель можно было использовать для моделирования пограничного слоя атмосферы и последующего изучения переноса пыли.

Разработчики программы COMSOL для моделирования аэродинамических процессов в приближении несжимаемой жидкости для турбулентного режима предлагают к использованию следующую систему уравнений: уравнения Навье – Стокса, осредненные по Рейнольдсу (4а), (4б) и (4в); уравнение неразрывности (5); уравнение нестационарного переноса тепла (6); ( к - в )-модель турбулентности (7а) и (7б) и ряд вспомогательных соотношений:

д и     д и     д и      д и

р--+ ри--+ р у--+ pw— дt     дx    ду     дz

д p   д (   д и А   д (   д и ]   д (    д и А _

-7“ + ТЛ птТ 1 + 7“1 птТ 1 + тН птТ 1 + Fx, дx  дx у   дx )  ду у  ду )  дz у   дz )

д у    д у    д у     д у    д p  д (   д у А  д (   д у А д (  д у А  _

+ р и + р у + р w =+I п_г 1 +I н_г 1 +I п_г 1 + F_v, д t    д x     д у     д z    д у   д x уд x ) д у у  д у ) д z уд z )   y

дw    дw    дw    дw   дp  д (  дw А  д (  дw А  д (  дw А  „ р--+ ри--+ ру--+ рw— =---1--пт— +--пт— +--лт— + F ,

T    T    Tz д1     дx     ду     дz    дz  дx у   дx)  ду у   ду)  дz у   дz)

(4а)

(4б)

(4в)

д и  д у   д w _

— + — + — = 0, д x  д у  д z

_ дЗ _ дЗ _ дЗ _ дЗ _ п д (, дЗА д ( . дЗА д р Сп--+ р Си--+ р Су--+ р Cw— = Q + qs З+--kT— +--kT— +— p дt     p  дx     p ду     p  д2       5   дx ( Т дx)  ду ( Т ду)  дг дк    дк    дк    дк           д (  дк)  д (  дк)  д ( дk р+ ри+ ру+ рw= nTP(и )+пт+1 пт 1+пт дt    дx    ду    дz          дx у  дx)  ду у  ду) дz удz дв     дв     дв     дв  Се1врТР(и)   д (   дг А  д (   дв А  д (   дв А р+ ри+ ру+ рw=+нт+1 пт 1+пт дt    дx   ду    дz      к     дx удx) ду уду) дz удz)

- рв,

^- C tiP-T, k

(7а)

(7б)

где P(и) = Vu : (Vu + (Vu)т); nr = рC ~; кг = Пт /Sc; t - время; u, v, w - компоненты вектора скорости потоков в направлении осей x, y, z соответственно; З - температура воздуха; p - плотность воздуха; p – давление; Cp – теплоемкость воздуха при постоянном давлении; Fx, Fy, Fz – компоненты вектора массовых сил по осям x, y, z соответственно; Q – источниковый член; qs – коэффициент теплопереноса; ПT - коэффициент динамической турбулентной вязкости; кт - коэффициент теплопроводности; к - удельная кинетическая энергия турбулентности; в - скорость вязкой диссипации энергии турбулентности; V - оператор Гамильтона; T - транспонирование; Sc - число Прандтля - Шмидта; Сц = 0,09, Св1 = 1,44, Св2 = 1,92, ик = 1,0, пв = 1,3 - константы (к - в)-модели турбулентности.

Рассмотрим возможности по модификации стандартной ( к - в )-модели турбулентности для выполнения расчетов аэротермодинамики атмосферы. В уравнениях ( к - в )-модели турбулентности, используемой авторами версии COMSOL 3.5а, не имелось возможности внесения изменений. Это, безусловно, недостаток. По мнению ряда исследователей, использование стандартной модели требует определенных модификаций модели, включающих изменение констант турбулентности, различных граничных условий для верхней и входной границы, добавление источниковых членов и т. д. ⁶ ( Baklanov et al., 1997; Baklanov, 2000; Alinot et al., 2002; Alinot et al., 2005; Balogh et al., 2012; Parente et al., 2010; Pontiggia et al., 2009; Russell, 2009; Blocken et al., 2007 ).

Уравнения Навье – Стокса, осредненные по Рейнольдсу, и уравнения теплопереноса содержат слагаемые (источниковые члены), которые можно использовать для модификации.

Перепишем систему (1)–(3) трехмерных уравнений термогидродинамики турбулентной атмосферы (без уравнения переноса влажности) в удобном для почленного сравнения в следующем виде ( Нормализация…, 1986 ):

du   du   du

--+ u--+ v--+ w— dt    dx   dy dv   dv   dv

--+ u--+ v--+ w— dt    dx    dy

—

дп  , d (   du 1  d \    du 1 d (d

--+ lv +--ц — +--ц — +--v — + J , ux                   uy                   uu dx     dx V   dx) dy V   dy)  dz V

д п dd y

i . d(

^{— lu 1} ~l ^Ц vx d x V

d v I d x )

. д ⁺т-| ц vy

5 y V

d v 1 d (  d v 1

I +1 v _v I + J_v d y )  d z V   d z )

d w   d w   d w    d w

--+ u --+ u --+ w— d t     d x     d y      dd z

д п  . _n. d (   d w 1   d \    d w 1   d (   d w 1

^—^⁺ ^ ^{9 +}~l ^ц »т I⁺^rl ^ц wyx I⁺^l^v wx I⁺ J w , d z        d x V    d x )  d y уд y )  d z V    d z )

d u   d v   d w

— + — + — = 0, d x   d y   d z

d^  d^  d^

--+ u --+ v --+ w d t     d x d y

d9'       d ( d^

--+ dw =— ц--- x9

d z        d x V     d x

d( d9' 1 д( д^Л l Цy3 '       I+ л lv9 '       I+ R9 + J9 ', dy V    dy )  dz V   dz )

(8a)

(8б)

(8в)

где ц^, ц_{а y}, v_a ( a = u, v, w, 9 ’) - горизонтальные и вертикальные коэффициенты турбулентности для количества движения и тепла соответственно; l - параметр Кориолиса; 9’ - отклонения потенциальной температуры от фоновой; п - приведенное давление; X - параметр конвекции (плавучести) ( g/ T ) (знаменатель равен 273 К); S – параметр фоновой стратификации; J u , J v , J w – составляющие векторов, определяющих искусственные источники (стоки) импульса по осям; J – искусственные источники (стоки) тепла, работающие по заданному режиму; R ₉ - поток радиации.

Из почленного сравнения уравнений (1а)–(1в), (2), (3) и (8а)–(8в), (9), (10) определим необходимые модификации в уравнениях программы COMSOL:

• -    в уравнение (4а) добавляем F x = р lv (компонента силы Кориолиса);

• -    в уравнение (4б) добавляем F x = - р lv (компонента силы Кориолиса);

• -    в уравнение (4в) добавляем F_z = рХ9' (эффект плавучести);

• - в уравнение (6) добавляем Q = - р C p S w + р C p R ₉ (фоновая стратификация, потоки радиации) и используем условие q s = 0.

Итоговая система уравнений трехмерной модели имеет такой вид:

du     du    du     du    дп  д (  du 1  д (  du 1  д Г  du 1,

(11а)

(11б)

(11в)

p-- + p u --+ p v --+ p w— =---1--Пт— +--Пт— +— Пт— + P lv ,

TTT dt     dx    dy     dz    dx  dx V   dx)  dy V  dy)  dz V dv     dv    dv     dv    дп  д Г   dv 1  д Г   dv 1  д (  dv 1

p-- + p u --+ p v --+ p w -- =---1-- Пт-- +-- Пт-- +-- Пт-- — p lu ,

TTT dt     dx    dy     dz    dy  dx V  dx)  dy V  dy)  dz V dw    dw    dw    dw   дп  d (  dw 1  д (  dw 1  д (  dw 1.

p-- + p u --+ p v --+ p w— =---1-- n_T— +-- n_T— +--Пт— + p^ 9 ,

TTT dt     dx     dy     dz    dz  dx V   dx)  dy V   dy)  dz V du dv dw n — + — + — = 0, dx dy dz

_ d3 _ d3 _ d3 _d9'

p C„--+ pCu--+ pCv--+ p C„w= p d t     p dx     p dy     p

_      C            . d(, d9'\ , d (, 59'1 , d (, d9'A

= —pC„Sw + pC„Rn +--kT--- +--kT--- +--kT , p              p 9              T                        /T dx V   dx )  dy V   dy ) dz Vd

dk     dk     dk     dk     _      д (   dk 1 д \   dk 1 д (dI p+ pu+ pv+ pw= nTP(u )+nT+1 Пт I+Пт dt     dx    dy     dz           dx V   dx)  dy V   dy)  dz Vd de     de     de     дв  C81enTP(u) d (   de 1  д (   дг 1  д (   дг1

p+ pu+ pv+ pw=^^+1 Пт I+1 Пт     I+1 Пт I dt     dx    dy     dz       k      dx V  dx)  dy V  dy)  dz Vd

—

ρε,

— C b2p^" . k

(14а * )

(14б * )

Двухмерная математическая модель

Переход к двухмерной задаче (координаты X – Z ) достаточно простой: исключаем все члены с переменной у , силу Кориолиса в уравнениях сохранения импульса и радиационные потоки в уравнении сохранения энергии. Именно с плоской задачи предполагается начать построение компьютерных моделей:

du    du     du    dn  d (  duA

d

+ — d z

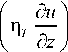
(15а)

(15б)

(18а)

(18б)

p--+ pu--+ pw— =---1--1 Пт — I dt     dx     dz    dx  dx v   dx dw    dw    dw   dn  d (  dwA  d (  dwAл p--+ pu--+ pw— =---1--Пт— +--Пт— + px9 , dt      c)x      dz     dz  dx V T dx )  dz V T dz )

du

— + — = 0, dxd d9' ,     _ d9' ,     .59'             , d (, d^'A, d (, d9'A pCn--+ pC.u--+ pC.w---= -pCnSw +--kT--- +--kT , p dt      p  dx     p  dz       p     dx V T dx )  dz V T dz)

d k      d k      d k     __ z_x d (   d k A d (d

ρε,

p+ pu+ pw= ПтP(u )+Пт+Пт-dt     dx     dz            dx V   dx)  dz Vd de     de     de  Ce1enTP(u)   d (   de A  d (   de A„ p--+ pu--+ pw— =--+--1 Пт — I+--1 Пт — I-C?p —.

dt     dx     dz       k       dx V   dx)  dz V   dz)

Коэффициент турбулентного переноса тепла в уравнении (17) определяется посредством осреднения коэффициента турбулентной вязкости по области моделирования с поправкой на число Прандтля – Шмидта ( Теодорович, 1988 )].

Таким образом, предстоит выполнить следующие дополнения:

• – в уравнениях сохранения импульса для горизонтальной компоненты источниковый член равен нулю J_u = 0, а для вертикальной компоненты следует добавить член, учитывающий эффект плавучести J^_ =+ p . X -9' [кг(м²^с²)];

• - в уравнении переноса тепла включен источниковый член Q = — S - C_p - p - v (Вт/м³). Коэффициент q_s

в уравнении теплопереноса равен нулю ( q s = 0).

Параметр фоновой стратификации атмосферы определяем как S = y a - у , где у - градиент температуры, у a - адиабатический градиент температуры (сухоадиабатический градиент температуры равен -0,01 °С/м).

Напомним, что если у < -ya, то атмосфера стратифицирована неустойчиво (развивается конвекция); если у > -уa, то атмосфера стратифицирована устойчиво (конвекция подавляется). В соответствии с терминологией, указанной в документе "Изменение потенциальной температуры с высотой при различных видах стратификации атмосферы"7, где можно найти вывод параметра фоновой стратификации как d9  А    zd9_

— = 9 / T - (Ya — y), следует, что при сухонеустойчивой стратификации — < 0, при сухобезразличной dz           a d9  .                d9 .

— = 0, при сухоустойчивой стратификации — > 0, что согласуется с выводами, полученными качественным dz методом.

Начальные и граничные условия модели

Используемые при описании граничных и начальных условий обозначения подробно описаны в документации программного продукта COMSOL.

Начальные условия при t = 0 таковы: u = u ( x ) ; 9' = 0; п = п₀; k = k ₀; 8 = е₀.

Граничные условия ( H – верхняя граница модели) приняты как в исходной модели, так и установлены по умолчанию разработчиками программы (табл. 1).

Для параметров турбулентности использованы следующие граничные условия, которые установлены по умолчанию разработчиками программы (табл. 2).

Таблица 1. Граничные условия Table 1. Boundary conditions

Условие	Граница
и = и ф ( z ) , w = 0, 3= 0	Входная граница 0 <  z <  H
n ( - kT ( V3 ' ) ) = 0	Выходная граница 0 <  z <  H
П7 ( V u + ( V u ) T ) n = 0, п = п0 (отсутствие вязкого напряжения)
и = и ф ( H ) , w = 0, 3= 0	Верхняя граница z = H
3 = f ( x , z ’ t )	Подстилающая поверхность z = 8 ( x )
,            T\    Г             f In (8 +)      Yl n - и = 0, nr (V и + ( V и ) T ) n = p C '’25 k °'25 / —    + C+  и \                /                              к L            V             7J (логарифмическая функция стенки)

Таблица 2. Граничные условия для параметров турбулентности Table 2. Boundary conditions for turbulence parameters

Условие	Граница
k = k 0, e = 80	Входная граница
n -V k = 0, n -V e = 0	Выходная граница
k = k 0, e = e0	Верхняя граница
n - V k = 0, e = C15k 1’5 / ( к8 w ) ,  8 + w = 8 „ p C °,25 k °’5 / n (логарифмическая функция стенки)	Подстилающая поверхность

Таким образом, в результате выполненных преобразований система уравнений (15а), (15б), (16), (17) становится подобной системе уравнений, описанной в работе ( Бакланов, 1988 ), с соответствующим набором краевых условий, т. е. в рамках коммерческого программного продукта COMSOL создана аэротермодинамическая модель микроклимата атмосферы, которая учитывает параметры конвекции (плавучести) и фоновой стратификации.

Геометрическое представление аэротермодинамической модели

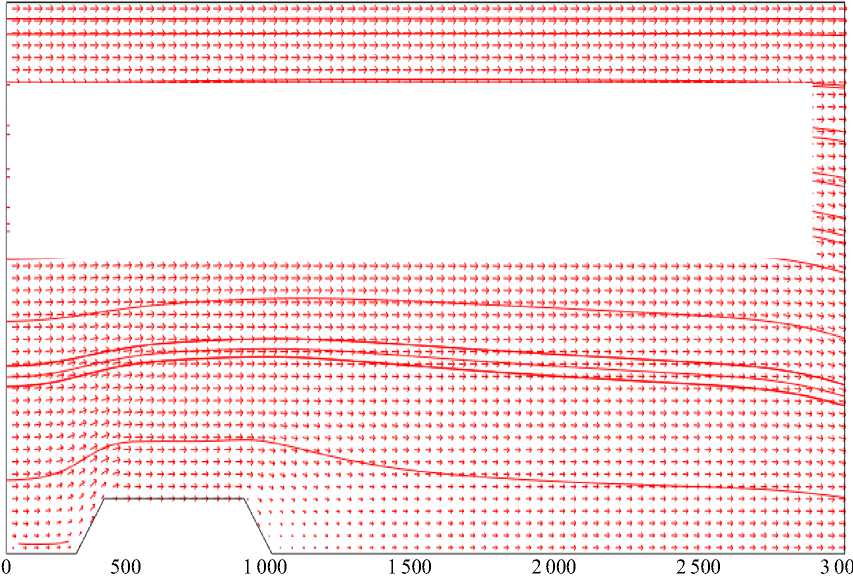
Работоспособность предлагаемого подхода проверена на модели, геометрия которой представлена на рис. 1, а и б . Размер области моделирования составляет 3 000 × 1 000 м. В координатах 250 и 950 м вдоль горизонтальной оси находятся начало и конец возвышенности высотой 100 м (в координатах 350 – 850 м – будущий источник пыления).

Результаты расчетов и обсуждение

Для тестирования модели приняты следующие значения:

• –    горизонтальная компонента скорости 5 м/с (на высоте +10 м над основанием модели; на верхней границе фиксируется значение, определяемое по логарифмическому закону 9,337 м/с);

• –    отклонение потенциальной температуры на границе раздела "земля – воздух" равно 0 °С;

• –    значение параметра стратификации варьируется в диапазоне от –0,05 до +0,05 °С/м с шагом 0,01 °С/м. Положительные значения должны обеспечить выстраивание инверсионных состояний атмосферы, а отрицательные – стратифицированно неустойчивых состояний. Предполагается варьировать параметр фоновой стратификации в указанном интервале, чтобы оценить его влияние на величину вертикального потока массы пыли (ВПМ), который рассчитывается по зависимости, указанной в работе ( Westphal et al., 1988 ), как функции 4-й степени динамической скорости.

Эффект влияния параметра стратификации на структуру потока выявлен посредством сравнения местоположений и формы линий тока, отвечающих различным значениям параметра фоновой стратификации. В частности, на рис. 1, а и б представлены расчетные поля скорости и линии тока для двух крайних значений параметра фоновой стратификации (–0,05 и +0,05 °С/м). Несмотря на простую геометрию модели, отклонения в местоположениях и формах линии тока достаточно очевидны, хотя и не столь значительны. Анализ осредненной по области моделирования величины коэффициента турбулентной вязкости свидетельствует о том, что интервал изменения для двух крайних значений параметра фоновой стратификации не превышает 4 %.

1 000

		►4444444444444444444- >44444 4 44 44 44444-1-1-1-1-)		'4 4 444 4 4444—44- 4	44- -*4-
444 4444-		>444-	*4*4 > 4 4 4 4 4 4 4 4 4 4 >4444444444444444	444444444444444 4 4 444 444 444 4 44 4-		>444 >444	444е 444-	*44- ->44-	> M M M M ) > > >  >444444444444	-44^ 4444	4 4
4444 4444		>444-	>4444 44444444444444 444444 444444444^4 Г-Г-» 4444->4 444-4-*-*4 -t > 1 ! > i i 1 i » > i s > -n ^ 444^-				444-		444444 44444444444		44-
		H>4-	>444444444444444- УНЭТТ-Н-?444444444	4444444444444 4444444444444	4 4-	1444444-		>44-	>444444444444 >444 444444444 Т4 44 4 44=Г=т=г-№*	444444-
	4-L=L= 444-	W-^T >444-	>TT44444444444444 f-1444444444444 > > >4444444444444444	Л")1">1">444 4 4 4^ 4444444444444	44-	^444444-		>44-	Н5ч^1ч-4-4-*4-42	^Д44	44^

а

1 000

0         500          1000          1 500         2000         2500         3000

б

Рис. 1. Расчетное поле скорости и линии тока для двух значений параметра фоновой стратификации: –0,05 °С/м (а); +0,05 °С/м (б) Fig. 1. Calculated velocity field and streamlines for two values of the background stratification parameter: –0.05 °С/m (а); +0.05 °С/m (б)

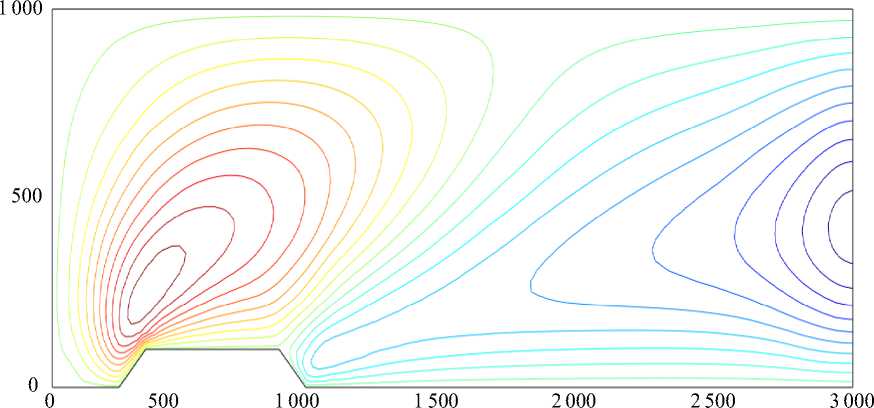
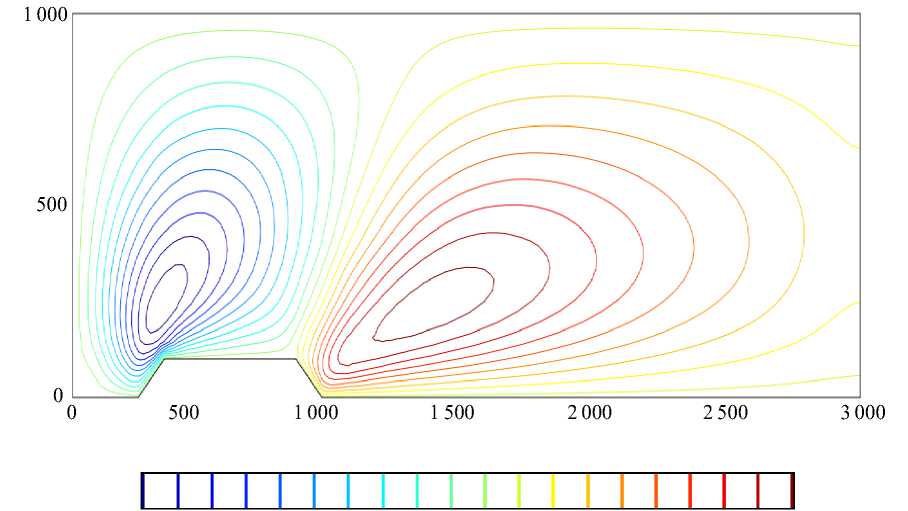
Эффект влияния параметра стратификации на пространственное распределение отклонений потенциальной температуры от фоновой качественно и количественно отражены на рис. 2, а и б . Изолинии построены на один и тот же момент времени (практически стационарный режим, время расчета продлено до 14400 с) при отрицательном и положительном значении параметра фоновой стратификации (использовано одинаковое количество изолиний).

–0,878             –0,515            –0,151            –0,212            0,576         0,849

а

–0,882             – 0,549            – 0,217            0,116            0,448         0,698

б

Рис. 2. Пространственные распределения отклонений потенциальной температуры от фоновой для двух значений параметра фоновой стратификации: –0,03 °С/м ( а ); +0,03 °С/м ( б ) Fig. 2. Spatial distributions of potential temperature deviations from the background temperature for two values of the background stratification parameter: – 0.03 °С/m ( а ); +0.03 °С/m ( б )

При отрицательном значении параметра фоновой стратификации положительные значения отклонений потенциальной температуры прогнозируются в левой части области моделирования, а отрицательные значения – в правой. При положительном значении параметра наблюдается обратная картина: в набегающем потоке – отрицательные отклонения потенциальной температуры, а вниз по потоку – положительные. Форма изолиний также имеет существенные различия, особенно в правой части области моделирования.

Количественные эффекты влияния параметра фоновой стратификации на аэротермодинамику атмосферы показаны на рис. 3–5.

Распределение отклонений потенциальной температуры от фоновой по высоте (до 350 м) вдоль вертикальной оси, восстановленной к основанию в точке с координатой 2 500 м, представлено на рис. 3. Кривые, расположенные выше оси абсцисс, соответствуют положительным значениям параметра фоновой стратификации (инверсионные состояния). Графики, расположенные ниже оси абсцисс, соответствуют отрицательным значениям параметра (стратифицированы неустойчивые состояния).

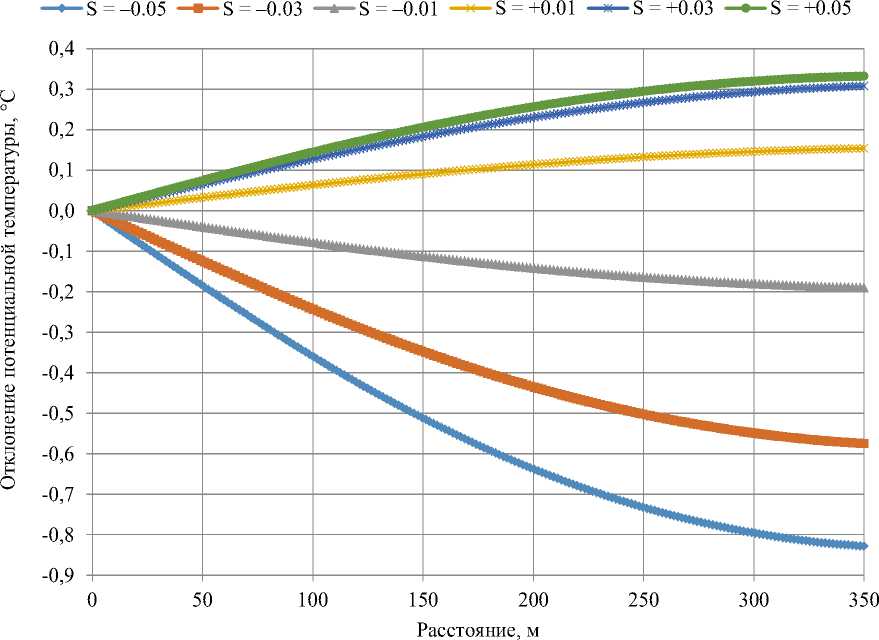
Рис. 3. Распределение отклонений потенциальной температуры от фоновой вдоль вертикальной оси при вариации параметра фоновой стратификации Fig. 3. Distributions of deviations of the potential temperature from the background temperature along the vertical axis with variation of the background stratification parameter

Несимметричность расположения кривых относительно горизонтальной оси соответствует определению параметра фоновой стратификации. Поведение кривых объективно отражает физику процесса. С ростом абсолютной величины параметра фоновой стратификации увеличивается модуль среднего значения градиента отклонений потенциальной температуры.

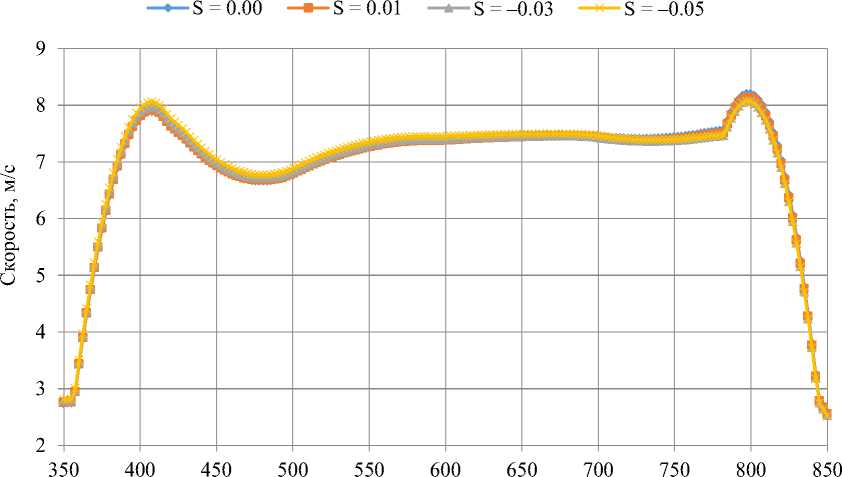
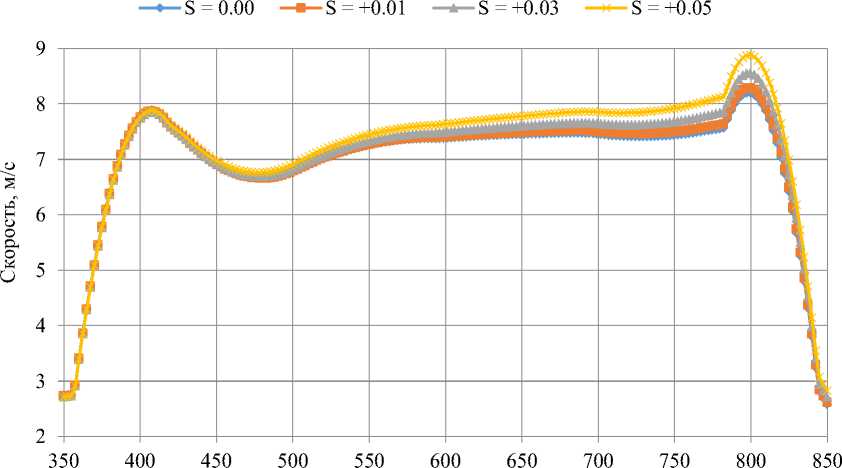
Для выполнения расчетов переноса пыли ( Амосов и др., 2018 ) требуется знание ВПМ пыли, поэтому выполнен анализ поведения горизонтальной компоненты скорости воздуха над источником пыления. На рис. 4, а и б изображены кривые горизонтальной компоненты скорости при отрицательных и положительных значениях параметра фоновой стратификации соответственно.

Эффект параметра стратификации достаточно нагляден. Если для отрицательных значений параметра в области "плато" поведение кривых достаточно похожее, то для положительных значений параметра, наоборот: в правой половине источника пыления кривые начинают заметно расходиться и значения экстремумов увеличиваются (почти до 9 м/с).

Расстояние, м

а

Расстояние, м

б

Рис. 4. Распределение горизонтальной компоненты скорости над источником пыления при отрицательных ( а ) и положительных ( б ) значениях параметра стратификации

Fig. 4. Distribution of the horizontal velocity component over the dust source with variation of the stratification parameter: a – negative; б – positive

Интересно проследить за осредненными значениями горизонтальной компоненты скорости и, как следствие, динамической скорости на высоте пыления и ВПМ ( Амосов и др., 2018 ), с увеличением параметра фоновой стратификации (от отрицательного к положительному). Расчетные значения динамической скорости на высоте пыления в зависимости от параметра фоновой стратификации приведены в табл. 3.

Таблица 3. Значения динамической скорости на высоте пыления при вариации параметра фоновой стратификации Table 3. Dynamic velocity values at dusting height with variation of the background stratification parameter

Параметр стратификации, °С/м	Динамическая скорость, м/с
–0,05	0,54479
–0,04	0,54316
–0,03	0,54186
–0,02	0,54105
–0,01	0,54094
0,00	0,54176
0,01	0,54370
0,02	0,54685
0,03	0,55112
0,04	0,55630
0,05	0,56209

Графическое изображение функции вертикального потока массы, который рассчитан в зависимости от параметра фоновой стратификации ( Westphal et al., 1988 ), представлено на рис. 5. В результате расчета прогнозируется сложное поведение величины ВПМ с переходом атмосферы из неустойчивого состояния в инверсионное с минимумом при значении, близком к сухо- и влажноадиабатическому градиенту температуры; очевиден эффект асимметрии. Если за минимальное значение ВПМ принять величину интенсивности пыления на уровне 2,48 ∙ 10^–6 кг/(м²∙с), то можно отметить, что переход атмосферы в инверсионное состояние приводит к более значительному увеличению величины ВПМ, чем переход в неустойчивое состояние атмосферы: при инверсионном состоянии атмосферы наблюдается рост почти 17 %; при неустойчивом – прирост менее 3 %.

Представленный на рис. 5 график хорошо описывается квадратичной функцией от параметра стратификации. Вертикальный поток массы, рассчитанный по зависимости, указанной в работе ( Westphal et al., 1988 ), аппроксимируется с коэффициентом достоверности 0,9969 функцией (19):

F = 9,0527 - 10 - 5 ■ 5 ² + 3,1882 ■ 10 - 6 ■ 5 + 2,5022 ■ 10 - 6 . w

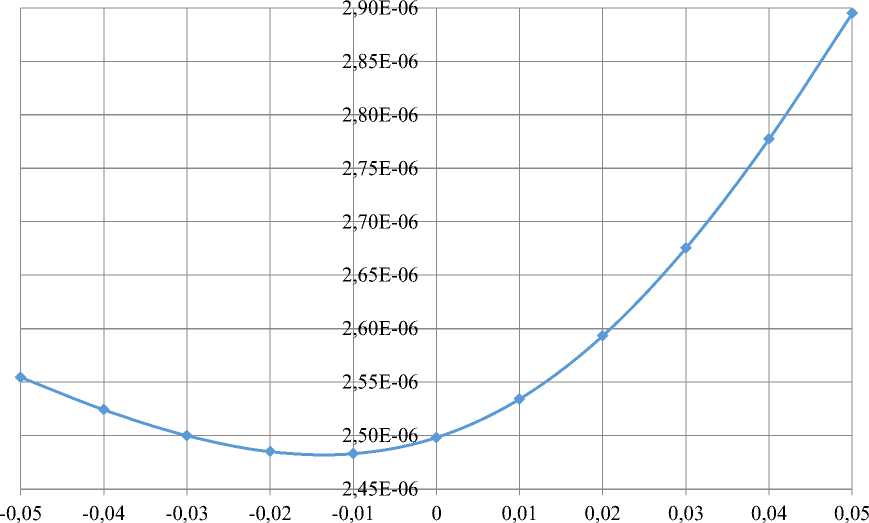
Рис. 5. Распределение вертикального потока массы при вариации параметра стратификации Fig. 5. Distribution of vertical mass flux with variation of the stratification parameter

Таким образом, минимум величины ВПМ соответствует значению параметра фоновой стратификации, составляющему примерно –0,018 °С/м. Такое поведение величины ВПМ в зависимости от параметра фоновой стратификации позволяет утверждать, что и уровень загрязнения атмосферы вниз по потоку в условиях инверсионного состояния атмосферы будет превышать загрязнение в условиях неустойчивой атмосферы.

Заключение

В результате проведенного исследования:

• –    представлен обзор исследований аэротермодинамики и загрязнения атмосферы, выполняемых с использованием неспециализированных программных комплексов вычислительной гидродинамики (CFD-моделирование) в приложении к задачам на объектах горной промышленности;

• –    обоснована необходимость усовершенствования CFD-моделей, используемых для прогноза загрязнения атмосферы при пылении хвостохранилищ и других объектов горнодобывающей промышленности (в том числе карьеров). В качестве направления совершенствования моделей при использовании неспециализированного кода COMSOL выбран подход, используемый при решении задач охраны окружающей среды Марчуком Г. И., Пененко В. В. и др.;

• –    описаны необходимые дополнения к программной среде COMSOL с целью учета в модели конвекции (плавучести) и параметра фоновой стратификации, обеспечивающих расчет аэротермодинамики атмосферы при различных состояниях атмосферы;

• –    создана в двухмерном варианте аэротермодинамическая модель микроклимата атмосферы, учитывающая параметры конвекции (плавучести) и фоновой стратификации, и апробирована на упрощенной модели хвостохранилища. При фиксированной скорости ветрового потока выполнены численные эксперименты и проанализированы аэродинамические параметры потоков, пространственные распределения отклонений потенциальной температуры в объеме модели; выполнены расчеты динамической скорости на высоте пыления и вертикального потока массы посредством зависимости, указанной в работе ( Westphal et al., 1988 );

• –    рассмотрена аналитическая зависимость прогноза вертикального потока массы от величины параметра стратификации; показана асимметричность (относительно сухо- и влажноадиабатического градиента температуры) величины вертикального потока массы по сравнению с неустойчивым и инверсионным состояниями. При инверсионных состояниях атмосферы величина вертикального потока массы пыли является максимальной, значит, и уровень загрязнения атмосферы вниз по ветровому потоку будет выше по сравнению с загрязнением при нейтральном или неустойчивом состояниях.

Представляется необходимым осуществить усовершенствование объемных авторских моделей и исследовать загрязнение атмосферы при вариации скорости ветрового потока в различных условиях состояния атмосферы. Кроме того, весьма интересным является применение подобной модели к задаче проветривания карьеров при проведении взрывных работ и эксплуатации оборудования с ДВС в условиях инверсионного состояния атмосферы.

Работа выполнена в рамках темы НИР № 1021051803680-5 "Процессы трансформации природных и техногенных систем в условиях изменения климата в Арктической зоне Российской Федерации (на примере Мурманской области)".