Разработка модели для недеструктивного определения площади и массы листа у кок-сагыза (Taraxacum kok-saghyz Rodin)

Одуванчик кок-сагыз (Taraxacum kok-saghyz Rodin, русский одуванчик) — восточно-тянь-шаньский редкий и эндемичный вид, травянистое растение-многолетник, произрастает на обедненных и солончаковых почвах, в 1930-1940 годы изучался в качестве местного каучуконоса и в настоящее время широко признан как один из наиболее перспективных источников природного сырья для производства резины (1, 2). Для кок-сагыза характерно наличие большого количества листьев, более 200, формирующих прикорневую розетку. Розетка чаще всего прижата к земле, плотная и состоит из продолговатых мясистых листьев. По форме пластинки они обратно ланцетно-яйцевидные, плотные, блестящие, гладкие, покрытые восковым налетом. Наружные листья почти цельнокрайние, ближе к центру розетки степень расчлененности листа увеличивается, и внутренние листья имеют более или менее струговидную форму, как у других одуванчиков, хотя выемки и доли у листьев кок-сагыза туповатые, без острых шиловидных зубчиков, зубчики встречаются в редких случаях (3). Хорошо известно, что площадь листа — важный показатель роста и развития растения (4, 5). Измерение площади и массы листа необходимо для расчета листового индекса (6), определения интенсивности фотосинтеза, эффективности поглощения света, потребления воды и питательных веществ, оценки урожайности растений (7-9). Такие свойства растения затрудняют прямой мониторинг состояния его надземных органов, следовательно, требуется разработать методы непрямого (неинвазивного) определения площади и массы листьев растения.

Среди различных подходов при биометрических исследованиях предпочтение отдается непрямым недеструктивным методам — недорогим, быстрым и простым в исполнении (6, 10). Кроме того, непрямые методы оценки позволяют исследователям изучать площадь и массу листьев на одном и том же растении в динамике в течении всего периода вегетации. Это существенно повышает надежность данных, снижая вариативность эксперимента (11-14). При недеструктивной оценке площади масса листа обычно оценивается по длине, ширине, сумме эффективных температур и длине черешка. Предлагаемые модели основаны на ростовых показателях с учетом формы листа у растения. Чаще всего рассматриваются корреляции длины и ширины листа с его площадью и массой (6, 15-17).

Хотя русский одуванчик изучался в течение десятилетий, до сих пор не были предложены предикативные модели для показателей площади и массы листа у этого растения. Такая модель впервые разработана нами и представлена в настоящем сообщении.

Цель работы состояла в создании надежной модели прижизненной оценки размера и массы листьев русского одуванчика на основе линейных измерений для анализа продуктивности зеленой массы растения в экологических, физиологических, генетических и селекционных исследованиях.

Методика . Растения кок-сагыза (коллекционные образцы Академии наук Heilongjiang) изучали в условиях города Харбина (Китай, N45°34'59.9'', E126°34'18.8'', июнь 2014 года). Климат умеренный муссонный, средняя годовая температура 4,2 ° С, среднегодовая норма осадков 532 мм. При выращивании растений использовали стандартную общепринятую технологию возделывания кок-сагыза.

Через 2 мес после посадки проростков на участке случайным образом с интервалом 14 сут отбирали по 50 репрезентативных неповрежденных листьев (всего 250 образцов). Для каждого листа определяли сырую массу взвешиванием на электронных весах (с точностью до 0,1 мг) и линейные размеры (длина и ширина, мм) обычной линейкой. Длину измеряли от кончика листовой пластинки до точки пересечения со стеблем, ширину — от края доя края в самой широкой части пластинки (округляли до ближайшего значения на миллиметровой шкале). Затем все листья последовательно пронумеровали, выложили на лист белой бумаги с измерительной линейкой, расправили, для чего накрыли прозрачной пластиковой пленкой, и сфотографировали. Изображения хранили в JPG формате. Фотографии обрабатывали в программе ImageJ v.1.48 (W. Rasband, «National Institute of Mental Health», США), рассчитывая площадь каждого листа. Детали метода подробно описаны ранее (18). Всего в предварительном калибровочном эксперименте определяли площадь, ширину и длину листовой пластинки, сырую массу для 250 листьев.

При установлении и калибровке модели использовали регрессионный анализ. Для 250 листьев оценивали взаимосвязи между площадью листа и массой как зависимыми переменными и длиной и шириной как независимыми переменными. Независимые переменные преобразовывали в другие функции (квадраты, квадратные корни и др.), чтобы установить линейные связи с площадью и сырой массой листа. По этим данным строили матрицы диаграмм рассеяния, используя программу OriginPro v.9.0 («OriginLab Corporation», США) для выявления линейных зависимостей между площадью и массой листа и преобразованными показателями длины и ширины листа. На основании матриц диаграмм рассеяния в программе SPSS v.19.0 646

(«IBM», США) получали уравнения моделей. Для применения выбрали уравнения с наибольшим коэффициентом детерминации (R²). Рассчитанные ( Sim.Yi ) и измеренные ( Obs.Yi ) значения площади листа сравнивали, оценивая достоверность уравнения регрессии и степень соответствия статистической модели реальной системе (R²). В итоге выбирали модель с наибольшей величиной R² при наименьшей среднеквадратичной ошибке (RMSE, root mean square error) (4). RMSE рассчитывали по формуле ( n — число измерений, в нашем случа е n = 250):

RMSE = \                  .

• V           л

  С целью валидации выбранной модели в октябре 2015 года на том же участке случайным образом отобрали 50 листьев растений кок-сагыза. Фактические значения показателей (длина, ширина, площадь и масса листа) определяли, как описано выше. Смоделированные величины площади и массы листа сравнивали с фактическими значениями методом регрессионного анализа. Уравнения регрессии в полученной линейной модели зависимости расчетных значений от фактических сравнивали с таковыми для

Наименьшая выборка 5 листьев

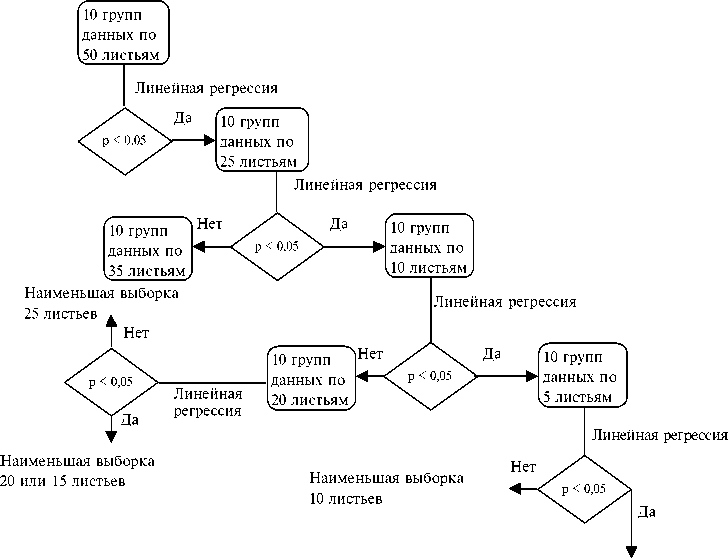
Рис. 1. Алгоритм определения размера выборки при использовании предлагаемой модели недеструктивной биометрии листа у кок-сагыза ( Taraxacum kok-saghyz Rodin).

модели равенства расчетных и фактических значений (линейного соответствия 1:1) при р = 0,05 (18). Регрессионный анализ выполняли в программе SPSS v.19.0. При оценке наименьшего размера выборки случайным образом из всего набора биометрических данных по 300 листьям формировали по 10 групп для числа листьев от 5 до 50. Площадь и массу листа рассчитывали для этих 10 групп, используя предложенную модель. Определяли линейные регрессии между рассчитанными и измеренными величинами. При статистической значимости (p) уравнения меньше 0,05 использованный размер выборки считали достаточным. Сначала тестировали

• 10 групп для 50 листьев, и если все коэффициенты уравнений линейной регрессии были достоверны при р < 0,05, переходили к тестированию набора данных по 25 листьям, продолжая процедуру до тех пор, пока не находили наименьший достоверный размер выборки.

Результаты. Использованную схему определения размера выборки для создания предлагаемой модели недеструктивной биометрической оценки растения иллюстрирует рисунок 1.

Разработка и валидация модели площади листа. Известная

особенность кок-сагыза — вариабельность морфологии листьев у разных растений, что актуализирует задачу разработки модели для

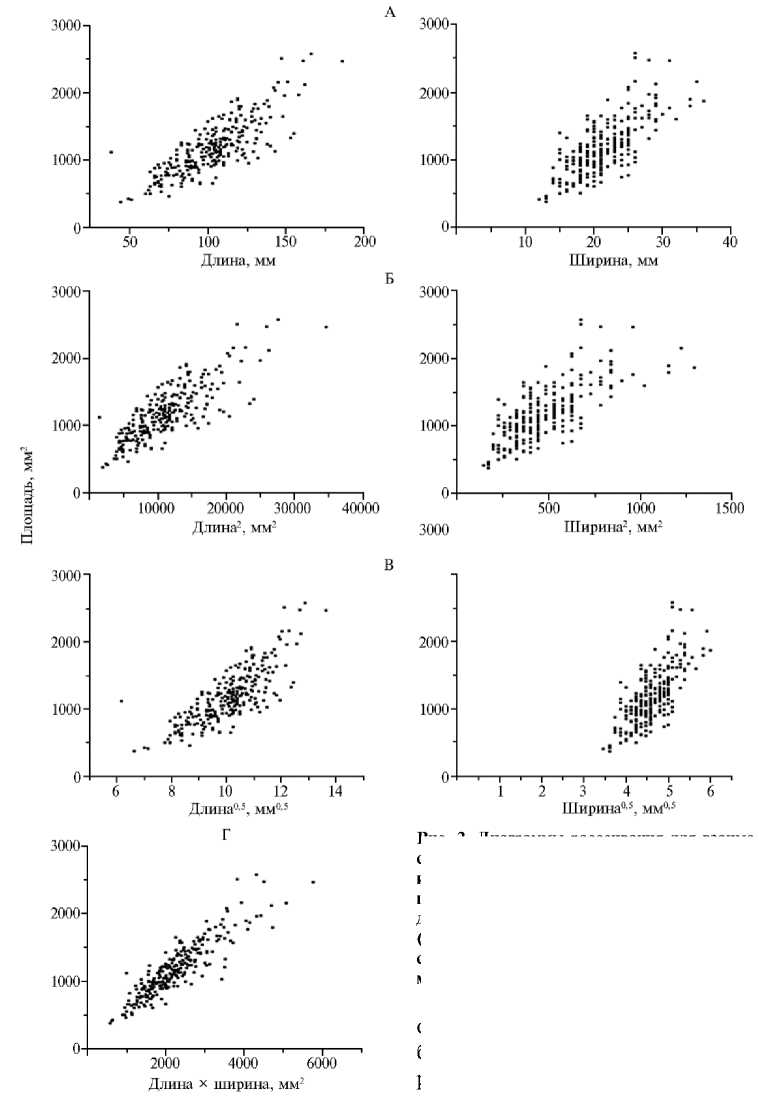
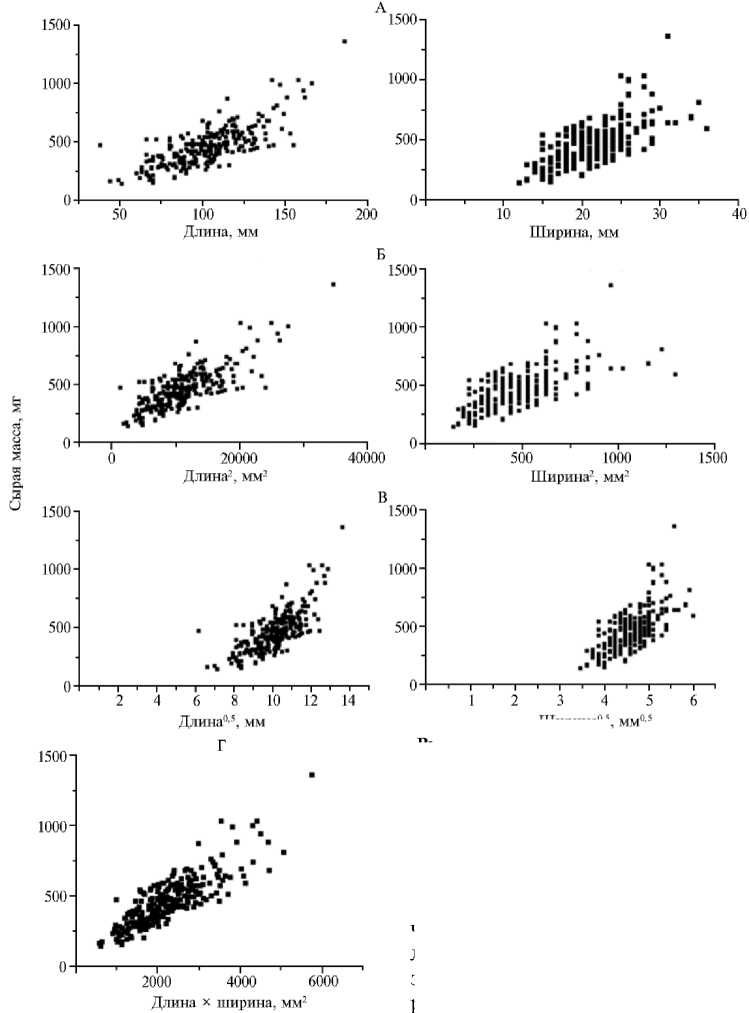
Рис. 2. Диаграммы рассеивания для взаимосвязи площади листа с непреобразованными и преобразованными значениями длины и ширина листа (А, Б, В) и с произведением длины на ширину (Г) у растений кок-сагыза ( Taraxacum kok-saghyz Rodin) в соответствии с предложенными линейными регрессионными моделями.

недеструктивной оценки их биометрических показателей.

Площадь листа была линейно связана с его длиной и шириной (A), квадратом длины и ширины (B), квадратным корнем из длины листа и ширины листа (C) и длиной листа, умноженной на ширину (D). Последовательно получили уравнения: LA = a + bL + cW; LA = a + bL2 + cW2; LA = a + bL0,5 + cW0,5; LA = a + bLW (табл. 1). Оказалось, что R2 возрастает, а RMSE уменьшается, если два разных преобразованных значения длины и ширины листа включить в одно уравнение регрессии. Если уравнение содержало три из четырех различных переменных (см. [9], [10], табл. 1), величина R2 была наибольшей и составила 0,818. Однако для [10] значение RMSE было ниже, чем для [9].

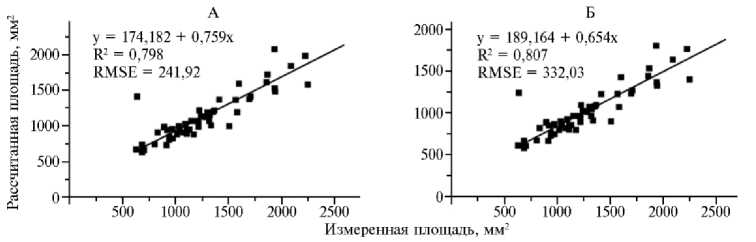
Рис. 3. Модели площади единичного листа у растений кок-сагыза ( Taraxacum kok-saghyz Rodin) при использовании уравнений [9] (A) и [10] (Б) (сплошная линия — линейная регрессия).

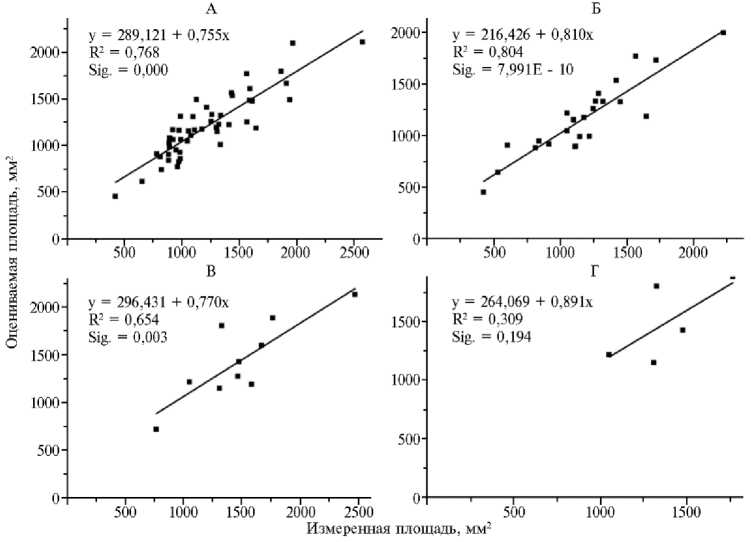
Рис. 4. Определение размера выборки для предложенной модели оценки площади листа у растений кок-сагыза ( Taraxacum kok-saghyz Rodin): 50 (А), 25 (Б), 10 (В) и 5 листьев (Г); Sig. — уровень значимости.

Валидация показала, что оценки площади листа с использованием моделей [9] и [10] были очень близки к фактически измеренной площади листа. Линейная регрессия взаимосвязи между измеренной и рассчитанной с помощью моделей площади листа были такими же, как для линии регрессии 1:1 при р = 0,05 (рис. 2, 3). При этом у модели [10] величина R2

• 1.    Линейные регрессионные модели для оценки площади листа у растений кок-сагыза (Taraxacum kok-saghyz Rodin)

  			Константа
  ¹	Набор переменных	Регрессионная модель	1               ,                   1                                   1                 ,                1 о 1                            1                            1	R2	RMSE
  			f a         b        c        d         e        f      g     h
  [1]	L, W	LA = a + bL + cW	- 744,204    9,962    42,043	0,810	171,96
  [2]	LW	LA = a + bLW	225,999    0,424	0,805	174,30
  [3]	L2, W2	LA = a + bL2 + cW2	222,184    0,047     0,907	0,810	171,87
  [4]	L 0,5 , W 0,5	LA = a + bL0,5 + cW0,5	- 2609,279  195,109   396,179	0,795	178,54
  [5]	L, W, LW	LA = a + bL + cW + dLW	- 356,135    6,274    23,674     0,171	0,813	170,74
  [6]	L, W, L2, W2	LA = a + bL + cW + dL2 + eW2	- 392,679    2,062    46,133     0,037       0,287	0,816	169,20
  [7]	L, W, L0,5, W0,5	LA = a + bL + cW + dL0,5 +e W0,5	711,166   25,248    38,795 - 306,976      29,071	0,816	169,00
  [8]	L0,5, W0,5, LW	LA = a + b(L0,5W0,5) + cLW	- 220,583    18,881     0,231	0,808	172,92
  [9]	L, W, L2, W2, L0,5, W0,5	LA = a + bL + cW + dL0,5 + eW0,5 + fL2 + gW2	6321,276   21,902   579,001 - 248,841    - 3346,881   0,002 - 3,984	0,818	168,34
  [10] L, W, L2, W2, L0,5, W0,5, LW		LA= a + bL + cW + dL0,5 + eW0,5 + fL2 + gW2 + hLW	6226,424   26,310   545,334 - 313,993    - 3138,047 - 0,009 - 3,866 0,057	0,818	168,29
  Пр	им еч ани е. L — длина листа, W — ширина листа, LA — площадь листа.

• 2.    Линейные регрессионные модели для оценки сырой массы листа у растений кок-сагыза (Taraxacum kok-saghyz Rodin)

  ¹	Набор переменных	Регрессионная модель	a      b 1 c zz d zz e zz f 1 gzh	R 2	RMSE
  [1]	L, W	FW = a + bL + cW	- 304,693     4,243    15,378	0,699	93,69
  [2]	LW	FW = a + bLW	74,630     0,172	0,703	93,00
  [3]	L2, W2	FW = a + bL2 + cW2	76,556     0,021     0,319	0,717	90,83
  [4]	L 0,5 , W 0,5	FW = a + bL0,5 + cW0,5	- 1041,233    81,679   147,543	0,678	96,85
  [5]	L, W, LW	FW = a + bL + cW + dLW	29,784     1,064     - 0,455     0,147	0,709	92,03
  [6]	LW, L2, W2	FW = a + bLW + cL2 + dW2	77,149     0,048     0,016     0,205	0,718	90,74
  [7]	L, W, L2, W2, L0,5, W0,5	FW = a + bL + cW + dLW + eL2 + fW2	- 45,050     - 4,630    32,631     0,086     0,033      - 0,587	0,734	88,11
  [9]	L, W, L2, W2, L0,5, W0,5, LW FW = a + bL + cW + dLW + eL0,5 + fW0,5 + gL2 + hW2		1125,572   - 24,857   233,070     0,055   276,956 - 1264,466 0,067 - 1,964	0,735	87,84
  Пр	им еч ани е. L — длина листа, W — ширина листа, FW — сырая масса листа.

была выше, чем в модели [9], поэтому в качестве итоговой модели выбрали [10].

Чтобы определить наименьший размер выборки в соответствии с моделью [10], сформировали 10 групп данных для 50, 25, 10 и 5 листьев, случайным образом выбранных из 300 анализируемых. Выполненный регрессионный анализ полученных оценок и результатов измерений показал,

50, 25 и 10 оценки ока-значимы при что для выборок из листьев полученные зались статистически

Ширина"’,

Рис. 5. Диаграммы рассеяния для взаимосвязи сырой массы листа с непреобразован-ными и преобразованными значениями длины и ширина листа (А, Б, В) и с произведением длины и ширины (Г) у растений кок-сагыза ( Taraxacum kok-saghyz Rodin) в соответствии с предложенными линейными регрессионными моделями.

р < 0,05. В то же время для некоторых величин уравнений линейной регрессии при выборке из 5 листьев р > 0,05 (рис. 4, Г). Из этого следует, что наименьший размер выборки при использовании модели [10] — 10 листьев.

Разработка модели определения сырой массы листа. Диаграммы рассеяния (рис. 5) показали, что длина и ширина листа, в том 651

числе преобразованные формы этих показателей (длина², ширина²; дли-на^0,5, ширина^0,5), а также произведение длины на ширину линейно связаны с сырой массой листа FW. Включив в одно уравнение все четыре формы показателей, получили итоговое уравнение регрессии с наибольшим значением R² и наименьшей величиной RMSE (табл. 2). Полученное уравнение регрессии: FW = 1125,572 - 24,857L + 233,070W + 0,055LW + + 276,956L^0,5 - 1264,466W^0,5 + 0,067L² - 1,964W².

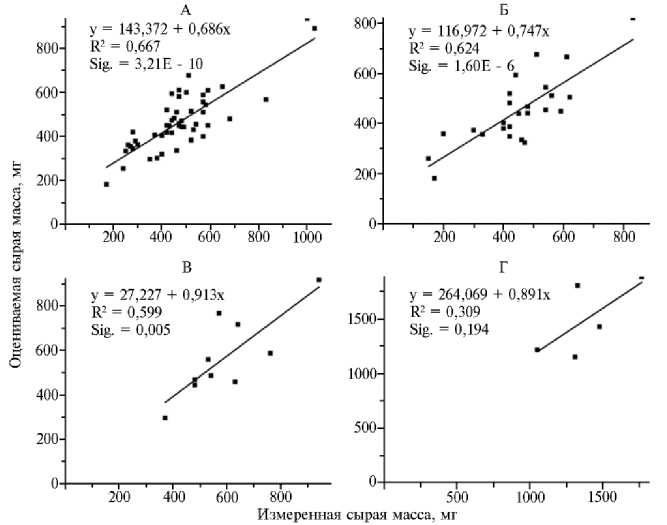
Рис. 6. Определение размера выборки для предложенной модели оценки сырой массы листа у растений кок-сагыза ( Taraxacum kok-saghyz Rodin): 50 (А), 25 (Б), 10 (В) и 5 листьев (Г); Sig. — уровень значимости.

Регрессионный анализ с целью определения минимального размера выборок для применения предложенной модели (рис. 6) показал результаты, сходные с отмеченными для площади листа (выборка, необходимая для получения статистически значимых оценок, — не менее 10 листьев).

Таким образом, было показано, что четыре преобразованные формы значений длины и ширины листа (собственно длина и ширина, длина² и ширина², длина^0,5 и ширина^0,5 и длина ½ ширина) связаны с площадью и сырой массой листа у кок-сагыза зависимостью, приближенной к линейной. Интеграция всех четырех форм в одно уравнение регрессии позволят предложить модель для недеструктивной оценки размера и массы листьев кок-сагыза. Предлагается следующе уравнение площади листа: LA = 6226,424 + 26,31L + 545,334W - 313,993L^0,5 - 3138,047W^0,5 - 0,009L² -- 3,86W² + 0.057LW (R² и RMSE соответственно 0,818 и 168,29). Для применения модели необходимы данные не менее чем по 10 случайно выбранным листьям. Для определения сырой массы листьев применяется уравнение FW = 1125,572 - 24,857L + 233,070W + 0.055LW + 276,956L^0,5 -- 1264,466W^0,5 + 0,067L² - 1,964W² (R² и RMSE соответственно 0,735 и 87,84). Необходимый минимальный размер выборки — 10 листьев. Предложенную модель в будущем следует валидировать для других сортов кок-сагыза. Объединение в одном уравнении регрессии преобразованных биометрических измерений, линейно связанных с площадью и массой листа, 652

может быть перспективно при работе с видами растений, для которых характерна высокая вариабельность размеров листовых пластинок.