Разработка модели для оптимизации структуры кредитного портфеля банка

MANAGEMENT OF THE BANK'S LOAN PORTFOLIO, THE OPTIMAL STRUCTURE OF THE MODEL, THE MAXIMUM LEVEL OF PROFITABILITY, ACCEPTABLE LEVEL OF CREDIT RISK ASSESSMENT OF THE QUALITY OF THE TOTAL LOAN

The article shows the need for the management of the credit portfolio of commercial banks with the help of a mathematical model. It allows to estimate the cumulative risk and return of the loan portfolio, as well as make decisions on granting credit to borrowers in terms of its impact on aggregate indicators of risk and return. Testing results indicate the practical significance of this study. The developed method of estimation and optimization of the loan portfolio can be used to improve management of the bank's credit policy and improve its competitiveness by reducing risk and increasing profitability of lending operations.

либо фактическом развитии неблагоприятного сценария в деятельности банка.

ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ. Поскольку кредитные операции занимают существенное место в деятельности коммерческих банков, целью исследования является оптимизация структуры кредитного портфеля банка с помощью математической модели. В ходе исследования применялись такие методы, как синтез, группировка, статистический анализ, математическое моделирование и программирование. Научная новизна исследования заключается в разработке модели для оптимизации структуры кредитного портфеля банка и её апробации на примере отчётных данных банка.

Для того, чтобы обосновать критерии оптимизации структуры кредитного портфеля банка, важно исследовать отдельные положения и категории, касающиеся теории кредитного портфеля.

В настоящее время среди экономистов отсутствует единая точка зрения в определении кредитного портфеля. Одни относят к кредитному портфелю все финансовые активы и даже пассивы банка, другие связывают его только со ссудными операциями банка, третьи подчеркивают, что кредитный портфель – это не простая совокупность элементов, а классифицируемая совокупность. Большинство исследователей считает, что «…кредитный портфель – это совокупность выданных ссуд, которые классифицируются на основе критериев, связанных с различными факторами кредитного риска или способами защиты от него» [1, с. 356].

Сущность кредитного портфеля коммерческого банка необходимо рассматривать на категориальном и прикладном уровнях. В первом аспекте кредитный портфель – это отношения между банком и его контрагентами по поводу возвратного движения стоимости, которые имеют форму требований кредитного характера. Во втором аспекте кредитный портфель представляет собой совокупность активов банка в виде ссуд, учтенных векселей, межбанковских кредитов и прочих требований кредитного характера, классифицированных по группам качества на основе определенных критериев [1, с. 347]. Ключевым моментом в управлении кредитным портфелем коммерческого банка является выбор критерия (критериев) оценки качества каждого кредита и всей их совокупности. В целом под качеством кредитного портфеля можно понимать такое свойство его структуры, которое обладает способностью обеспечивать максимальный уровень доходности при допустимом уровне кредитного риска и ликвидности баланса [1, с. 401].

Многие экономисты считают, что качество характеризует эффективность формирования кредитного портфеля банка с позиции доходности, степени кредитного риска и обеспеченности. Выбор данных критериев связан с тем, что высокая обеспеченность и доходность ссуды снижает вероятность ее невозврата или задержки, и тем самым повышает качество ссуды. Это верный подход, но он применим для анализа качества отдельного кредита, а не кредитного портфеля в целом. Так, обеспеченность нецелесообразно использовать для оценки качества кредитного портфеля, поскольку степень обеспеченности по каждому кредиту различна, а значит, различны степень риска и размер созданного резерва на возможные потери по ссудам, который банку все равно придется рассчитывать отдельно по каждому выданному кредиту. Поэтому при построении модели управления кредитным портфелем мы руководствовались двумя критериями – доходностью и риском.

Управление кредитным портфелем – это организация деятельности банка при осуществлении кредитного процесса, направленная на предотвращение или минимизацию кредитного риска.

При управлении кредитным портфелем конечными целями коммерческого банка являются:

• •    получение прибыли от ссудных операций;

• •    сохранение ликвидности и платежеспособности банка.

Процесс управления кредитным портфелем является неотъемлемой частью банковской деятельности и включает такие последовательные этапы реализации, как оценка кредитоспособности и вероятности дефолта заемщика, присвоение заемщику внутреннего кредитного рейтинга и определение величины потерь по кредиту в случае дефолта; определение цены кредита, и наконец, принятие решения о кредитовании заемщика с учетом влияния на показатели риска и доходности совокупного портфеля в соответствии с оптимальной кредитной стратегией банка.

Разработанная модель позволяет оценить совокупный риск и доходность кредитного портфеля, а также принимать решения о предоставлении кредита с точки зрения его влияния на совокупные показатели риска и доходности кредитного портфеля.

Пусть необходимо сформировать кредитный портфель на основе поданных заемщиками кредитных заявок i = 1…, N , объемом V₁ … V_N денежных единиц. Предположим, что общая сумма кредитных ресурсов банка составляет V , тогда весовой коэффициент каждого кредита ( w_i ) находится по формуле

W. = V i / V              (1)

где n_i – бинарная переменная, отражающая решение банка о предоставлении кредита, то есть n_i = 1, если заемщику i предоставлен кредит и n_i = 0, в противном случае. Тогда тот факт, что сумма предоставленных банком кредитов не должна превышать общий объем кредитных ресурсов банка, преобразуется в ограничение на сумму весовых коэффициентов:

NN i = li=l

Обозначим y_i – минимальную доходность по кредиту. Она определяется исходя из присвоенной заемщику категории кредитного рейтинга, вероятности дефолта ( PD ) и размера потерь по кредиту в случае дефолта заемщика. Размер потерь в случае дефолта принято обозначать LGD (Loss Given Default). LGD определяют индивидуально для каждого заемщика в зависимости от рыночной стоимости залога и другого обеспечения по кредиту.

Наибольшую сложность при определении минимальной доходности кредита составляет тот факт, что специалистам банка не доступна реальная цена кредита ( P_i ). Тем не менее, стоимость кредита может быть найдена на основе аналитического выражения как текущая дисконтированная стоимость потока платежей по кредиту с учетом вероятности дефолта ( PD ) и размера потерь в случае дефолта ( LGD ). Текущая дисконтированная стоимость по кредиту находится по формуле дисконтированного математического ожидания:

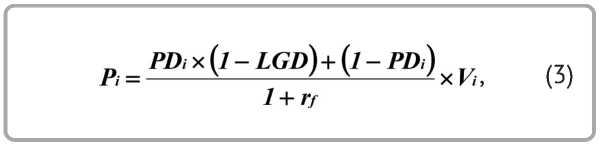
где r _f – безрисковая процентная ставка (ставка рефинансирования).

Тогда минимальная доходность ( y_i ) по кредиту i находится из выражения

PDix(l- LGP)+(1- PDi) 1 + rj

(1+yO

PDi x (/ - LGD)+ (/ - PDi) ’ y = (1 + rf) /PDi • (1 - LGD) + + (1 - PDi) - 1.

Данное выражение гарантирует выполнения условия y_i ≥ r _f , означающего, что доходность рискового актива должна быть больше безрисковой процентной ставки. При этом доходность по кредиту совпадает с безрисковой процентной ставкой лишь в случае отсутствия риска дефолта ( PD_i = 0 y_i = r _f ).

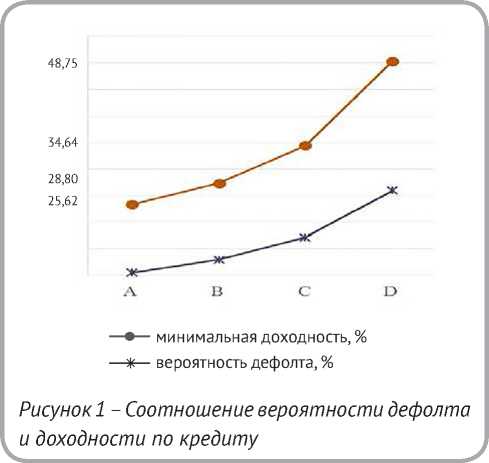
В таблице 2 приведены значения минимальных доходностей, рассчитанные для каждой категории кредитного рейтинга в предположении, что размер потерь в случае дефолта заемщика составляет 50 % (то есть LGD = 0,5) и безрисковая процентная ставка равна 25 % ( r _f = 0,25).

Полученные значения вероятностей дефолта и соответствующих им минимальных доходностей проиллюстрированы на рисунке 1. Увеличение риска дефолта заемщика сопровождается увеличением минимальной доходности по кре-

Таблица 1 – Вероятность дефолта каждой категории кредитного рейтинга
Рейтинг	Вероятность дефолта ( PD ), %
A	1,00
B	5,91
C	14,32
D	31,94

Таблица 2 – Минимальная доходность по кредиту Рейтинг Минимальная требуемая доходность по кредиту (y), % A 25,6281407 B 28,8062239 C 34,6402413 D 48,7563965 диту, требуемой банком. Тем не менее, полученные значения доходностей являются минимальными и учитывают лишь возможность дефолта заемщика, то есть кредитный риск. На практике доходность кредита превышает значения минимальной доходности, так как учитывает ряд дополнительных факторов. Например, создание обязательных резервов, резервов на потери по кредитам, длительность срока погашения кредита. Создание обязательных резервов увеличивает требуемую доходность по ссуде, так как резерв не является прибыльным для банка и служит для покрытия реализованных кредитных рисков. Кредиты, выданные на более длительный срок, также характеризуются более высокой требуемой доходностью.

Задача оптимизации кредитного портфеля с учетом ограничений может быть сформирована следующим образом:

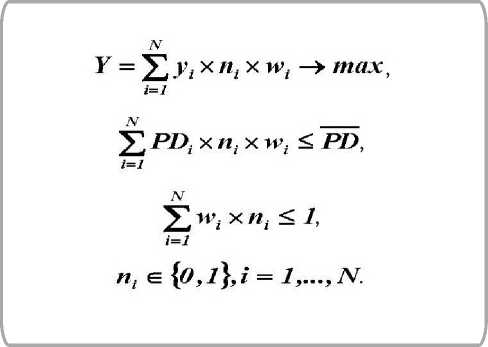
Сформированная задача отвечает условию максимизации минимальной доходности при ограничении, что вероятность дефолта должна быть ниже среднего значения, сложившегося в системе.

Необходимо подчеркнуть, что риск кредитного портфеля является одним из наиболее

существенных для банка и носит объективный характер. На корпоративных клиентов банка приходится более 95 % кредитного портфеля. Поэтому при анализе кредитного риска применяются методы риск–менеджмента как на портфельном уровне, так и уровне отдельных заемщиков. На уровне портфеля рассчитываются доля проблемных кредитов и сумма фактически созданного резерва на покрытие возможных убытков. Для конкретных заёмщиков используются внутренняя рейтинговая модель и методы финансового анализа. Однако Национальный банк Республики Беларусь до сих пор не разработал методику оценки агрегированного кредитного риска, позволяющую отслеживать количественные характеристики риска в динамике.

Мы предлагаем банку использовать методику расчета показателей совокупного кредитного риска банка [2]. Для этого была разработана табличная форма Excel, автоматически производящая расчеты по заданным формулам. Ниже приводится распределение объема кредитного портфеля по степени риска в таблице 3.

Затем осуществляем расчет возможной (ожидаемой) величины убытков по кредитному портфелю. [2, с. 59]. Это важнейшая характеристика кредитного риска, так как она служит центром распределения его вероятностей. Смысл данного показателя заключается в том, что он показывает наиболее правдоподобное значение уровня риска и определяется следующим образом:

и

,                    (6)

i = 1

> где Sð – величина убытков по кредитному портфелю; Si – сумма ссудной задолженности по i-й группе кредитов по степени риска, i = 1, 2, 3, …, n; n – количество групп активов по степени риска; pi (c) – степень риска по i-й группе кредитов по степени риска, %.

Результаты расчета данного показателя пред- ставлены в таблице 4.

Рассмотрим состав кредитного портфеля банка. В его структуре доля заемщиков с рейтингом A составляет 5 %, с рейтингом B – 50 %, с рейтингом C – 30 % и с D – 15 %. В качестве безрисковой процентной ставки возьмем ставку рефинансирования, равную 25 %. Размер потерь в случае дефолта заемщика будем считать равным 50 %.

Тогда можно рассчитать минимальную доходность кредитного портфеля, используя данные таблиц 3 и 4. Решение о выдаче кредита обозначим n_i . При этом n_i {0,1}, где i = 1…, 24, свидетельствующая о выдаче ( n_i = 1) или отказе в выдаче кредита ( n_i = 0).

Данные по расчету минимальной доходности кредитного портфеля банка и общей вероятности дефолта при выдаче кредита представим в таблице 5.

Минимальная доходность кредитного портфеля составляет 33,39 %, причем средняя веро-

Таблица 3 – Распределение кредитного портфеля по степени риска (категория качества ссуд)
Категория качества ссуд	Вид ссудной задолженности	Величина актива, у. е. ( S i )	Вероятность возникновения убытков, % ( p i ( c ))
I категория качества (высшая)	Стандартные	1 902 824	1
II категория качества	Нестандартные	2 474 957	10
III категория качества	Сомнительные	1 780 683	30
IV категория качества	Проблемные	244 280	50
V категория качества (низшая)	Безнадежные	25 716	100
Итого	Х	6 428 460	Х

Таблица 4 – Расчет ожидаемой величины убытков кредитного портфеля
Категория качества	Величина актива, у. е. ( S i )	Вероятность возникновения убытков, % ( p i ( c ))	S i * P i ( c ), у. е.
I категория качества (высшая)	1 902 824	1	19 028,24
II категория качества	2 474 957	10	247 495,7
III категория качества	1 780 683	30	534 204,9
IV категория качества	244 280	50	122 140
V категория качества (низшая)	25 716	100	25 716
V	S ð		948 584,84

Таблица 5 – Доходность кредитного портфеля банка

Рейтинг Доходность по кредиту (yt), % Объем кредитной заявки (w) Решение о выдаче кредита (n)) Итоговая доходность, (y. • wi • n.) % Вероятность дефолта (PDi), % Вероятность дефолта при выдаче кредита (PD = PDl • nl • w.), % A 25,6281407 0,05 1 0,8291457 1,00 0,050 25,6281407 0,10 0 0,0000000 1,00 0,000 25,6281407 0,15 0 0,0000000 1,00 0,000 25,6281407 0,20 0 0,0000000 1,00 0,000 25,6281407 0,30 0 0,0000000 1,00 0,000 25,6281407 0,50 0 0,0000000 1,00 0,000 B 28,8062239 0,05 0 0,0000000 5,91 0,000 28,8062239 0,10 0 0,0000000 5,91 0,000 28,8062239 0,15 0 0,0000000 5,91 0,000 28,8062239 0,20 0 0,0000000 5,91 0,000 28,8062239 0,30 0 0,0000000 5,91 0,000 28,8062239 0,50 1 9,7660879 5,91 2,955 C 34,6402413 0,05 0 0,0000000 14,32 0,000 34,6402413 0,10 0 0,0000000 14,32 0,000 34,6402413 0,15 0 0,0000000 14,32 0,000 34,6402413 0,20 0 0,0000000 14,32 0,000 34,6402413 0,30 1 7,4838432 14,32 4,296 34,6402413 0,50 0 0,0000000 14,32 0,000 D 48,7563965 0,05 0 0,0000000 31,94 0,000 48,7563965 0,10 0 0,0000000 31,94 0,000 48,7563965 0,15 1 5,7068904 31,94 4,791 48,7563965 0,20 0 0,0000000 31,94 0,000 48,7563965 0,30 0 0,0000000 31,94 0,000 48,7563965 0,50 0 0,0000000 31,94 0,000 Минимальная доходность кредитного портфеля, % 33,3900509 Вероятность дефолта, % 12,092 ятность дефолта заемщиков при данной структуре кредитного портфеля составила 12,092 %.

На основе модели сформируем оптимальный кредитный портфель банка, при котором его доходность была бы максимальной, при условии, что вероятность дефолта оставалась на прежнем уровне (12,092 %). Для этого составим программу оптимизации кредитного портфеля с помощью Delphi 7 или Pascal.

Условие программы проиллюстрируем с по- мощью рисунков 2 – 6.

Для того чтобы учесть все возможные варианты выдачи или отказа в выдаче кредита, используется алгоритм, представленный на рисунке 2, который позволит перебрать все возможные комбинации n_i .

На рисунке 3 описан алгоритм задания расчета доходности, доли заемщиков с различной категорией рейтинга и вероятности дефолта заемщиков.

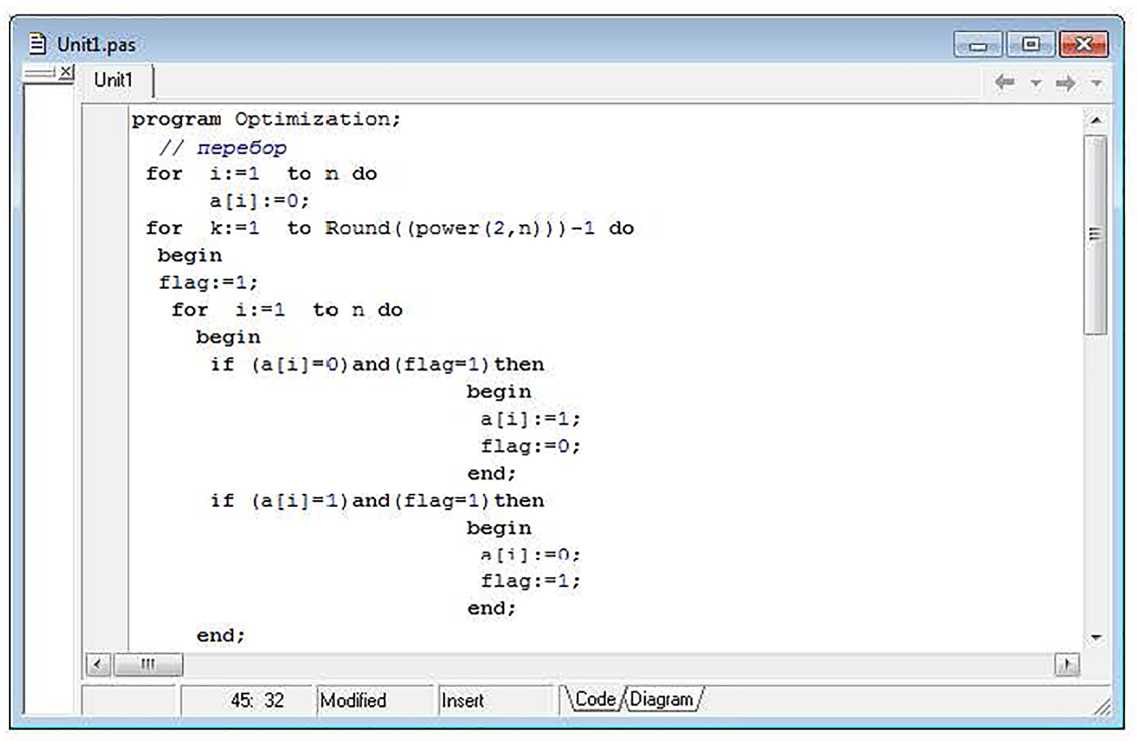
Рисунок 2 – Организация изменения n_i

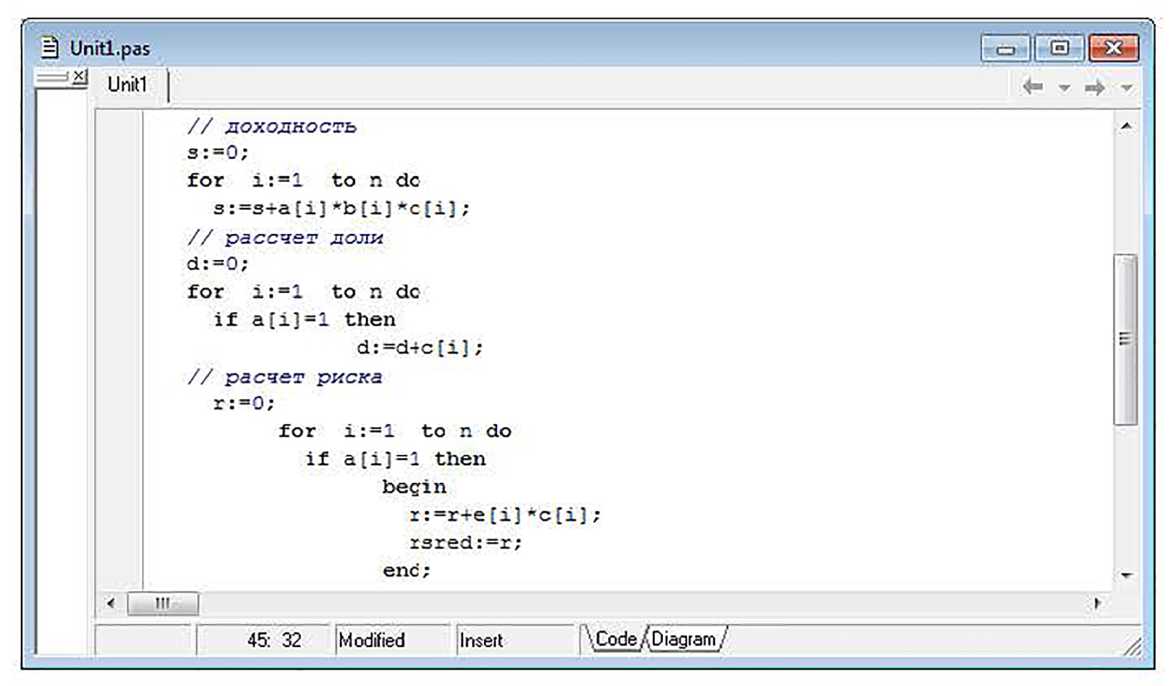
Рисунок 3 – Ограничения по доходности, доли, вероятности дефолта

Сама модель вместе с ограничениями представлена на рисунке 4. В данном случае мы стремимся к тому, чтобы минимальная доходность кредитного портфеля банка стремилась к максимуму, то есть программа из всех возможных вариантов выберет ту комбинацию, в которой доходность наибольшая. Также задаются ограничения по доле (так как банк не может выдать в кредит больше денег, чем у него есть у самого) и по вероятности дефолта, которая должна остаться на прежнем уровне, то есть не превышать 12,092 %.

В результате выполнения программы была получена оптимальная структура кредитного портфеля, при которой доходность составила существующим в таблице 6.

В полученном оптимальном кредитном портфеле доля заемщиков с рейтингом D сотавила 35%. В нашем примере банк не принимает решения о кредитовании заемщиков с рейтингом D самостоятельно, поэтому он не может повлиять на долю заемщиков с категорией рейтинга D. Чтобы сформировать оптимальный кредитный портфель банка, необходимо ввести ограничение: оставить долю заемщиков с рейтингом D на прежнем уровне 15 % ( меньше или равно). Других ограничений не будет, тогда модель оптимизации кредитного портфеля банка будет искать такое решение, чтобы минимальная доходность кредитного портфеля банка стремилась к

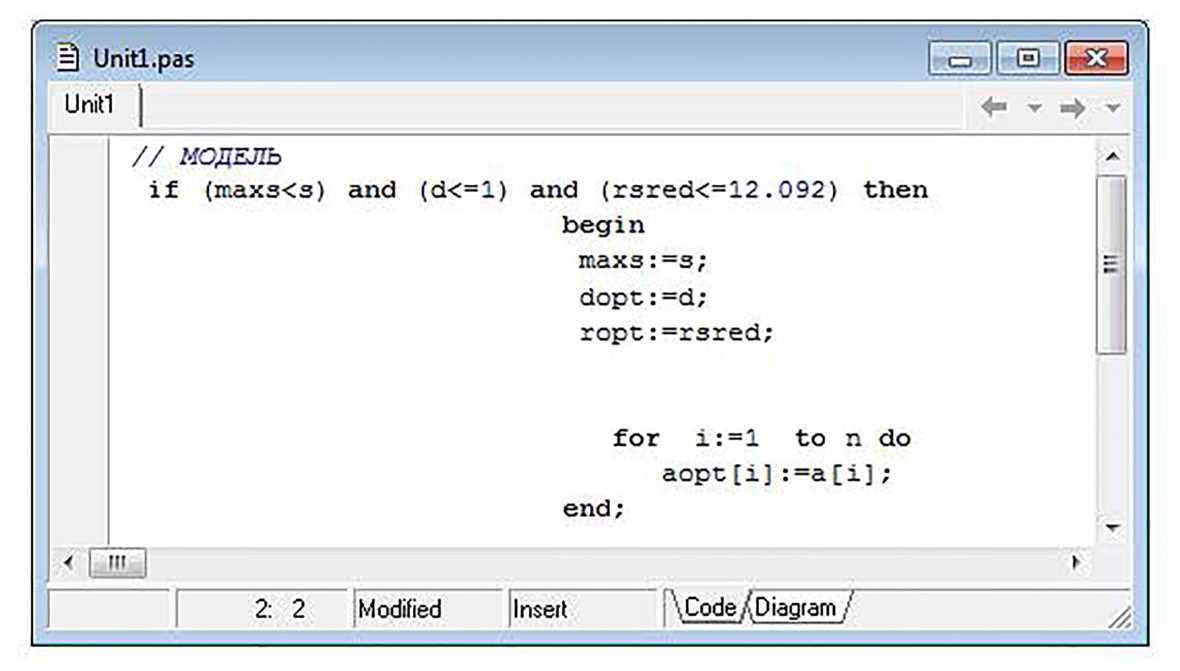
Рисунок 4 – Модель оптимизации кредитного портфеля

24,242 %, при этом средняя вероятность дефолта заемщика составила 12,075 %, что меньше, чем в первоначальном случае (рисунок 5).

Исходя из расчета программы, структура оптимального кредитного портфеля должна состоять таким образом, чтобы доля заемщиков с рейтингом A была равной 60 %, с рейтингом B – 5 % и с рейтингом D – 35 %. В этом случае банк получит доходность больше существующей, а риск останется на прежнем уровне. Для наглядности сравним полученный результат с

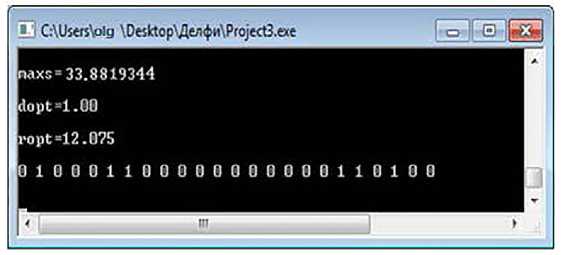
Рисунок 5  – Оптимальная структура

кредитного портфеля

У

Таблица 6 – Эффект от оптимизации структуры кредитного портфеля Вариант A, % B, % C, % D, % Доходность, % Вероятность дефолта, % Существующий 5 50 30 15 33,3900509 12,092 Предлагаемый (вариант 1) 60 5 – 35 33,8819344 12,075 Эффект, п. п. – – – – +0,4918835 –0,017     J максимуму, а совокупная вероятность дефолта заемщиков оставалась бы на прежнем уровне, то есть была бы меньше или равна 12,092 %.

При новом ограничении программа находит новое решение поставленной задачи, представленное на рисунке 6.

Исходя из нового решения, минимальная доходность кредитного портфеля банка будет равной 33,479 % при вероятности дефолта заемщиков 12,062 %. Полученная минимальная доходность с учетом ограничения по доли заемщиков с рейтингом D меньше, чем в первом случае, однако все равно больше существующей доходности филиала банка.

Структура заемщиков с различной категорией рейтинга во втором варианте сложится следующим образом: заемщики с рейтингом A со-

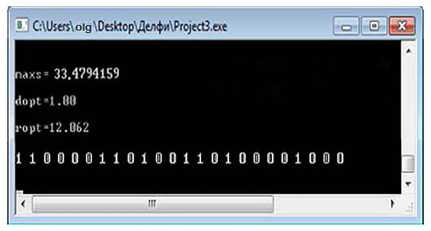
Рисунок 6 – Оптимальная структура кредитного портфеля с учетом нового ограничения ставят 15 %, с рейтингом B – 35 %, с рейтингом C – 35 % и количество заемщиков с рейтингом D останется на прежнем уровне, то есть составит 15 % (таблица 7).

Модель оптимизации во втором варианте позволит увеличить минимальную доходность кредитного портфеля на 0,089 п. п., а средняя вероятность дефолта заемщиков при этом снизится на 0,030 п. п.

ВЫВОДЫ

Используя данную программу, можно сформировать оптимальный кредитный портфель банка с определенной вероятностью дефолта заемщика, причем в приведенном примере доля каждой категории рейтинга могла принять значения только 5, 10, 15, 20, 30 и 50 %, что не является пределом. Если изменить долю каждой категории заемщика или увеличить их количество, то увеличится и масштаб анализа. Апробация результатов доказала практическую значимость данного исследования. Разработанная методика оценки и оптимизации кредитного портфеля может быть использована для совершенствования системы управления кредитной политикой банка и повышения его конкурентоспособности, путем снижения риска и роста доходности кредитных операций.

Таблица 7 – Эффект от оптимизации структуры кредитного портфеля с учетом ограничения по доли заемщиков с рейтингом D
Вариант	A, %	B, %	C, %	D, %	Доходность, %	Вероятность дефолта, %
Существующий	5	50	30	15	33,3900509	12,092
Предлагаемый (вариант 2)	15	35	35	15	33,4794159	12,062
Эффект	–	–	–	–	+0,089365	–0,030      J