Разработка модели финансового состояния, прогнозирование на основе множественной регрессии

Автор: Сафарян С.А.

Журнал: Экономика и бизнес: теория и практика @economyandbusiness

Статья в выпуске: 12-3 (70), 2020 года.

Бесплатный доступ

В условиях нестабильности экономических колебаний, особую актуальность приобретает выбранная модель оценки финансового состояния. В работе представлена модель, которая позволяет проанализировать не только основные показатели финансового состояния, но и выявить причинно-следственные связи между ними. В условиях микроклимата организации главным инструментом выступает корреляционный и регрессионный анализ, который позволяет качественно измерить и выявить форму влияния, по итогам которой можно построить математическую модель и уже по ней прогнозировать финансовое состояние организации в будущем.

Методика, теснота связи, финансовое состояние, корреляция, прогнозирование

Короткий адрес: https://sciup.org/170182403

IDR: 170182403 | DOI: 10.24411/2411-0450-2020-11129

Текст научной статьи Разработка модели финансового состояния, прогнозирование на основе множественной регрессии

Линейные по параметрам и по переменным множественные регрессионные модели могут быть представлены в виде [1]:

Ү=bО +b!xj+ где Y – результативный показатель;

b 0 , b 1 , b k – неизвестные параметры модели; ε – случайные ошибки модели.

В случае моделирования финансового состояния с помощью множественного корреляционно-регрессионного анализа в качестве результативного показателя была принята чистая прибыль.

Данный показатель является обобщающим и в случае построения корреляционно-регрессивной модели является зависимой переменной как для платёжеспособности, так и для финансовой устойчивости.

По итогам выбора факторных показателей можно построить модель, с помощью которой можно дать достоверный прогноз.

Отбор переменных, вошедших в итоговую модель, производился на основе ме-

Х1 = выручка;

Х2 = себестоимость;

Х3 = текущий налог на прибыль;

Х4= прибыль от продаж;

Х5 = основные средства;

Х6 = дебиторская задолженность;

Х7 = денежные средства;

^b2^xj +⋯+bк^xк+ε (1)

тода пошаговой регрессии. Критериями выбора наилучшей регрессионной модели являлись значение скорректированного коэффициента детерминации R adj² , значимость всех коэффициентов модели по критерию Стьюдента, значимость модели на основе критерия Фишера, а также значение коэффициента корреляции между фактическим значением зависимой переменной и расчетным, найденным по модели.

В качестве показателей-факторов, потенциально влияющих на значение прибыли, использованы ключевые финансовые величины:

Х8 = прочие расходы;

Х9 = Управленческие расходы;

Х10 = кредиторская задолженность;

Х11 = запасы;

Х12 = собственный капитал.

Проведение статистических исследова- вых отчётов ООО «КраСур» за 5 лет был ний, в частности регрессионного анализа, сформирован исходный массив для анали-невозможно без массовых наблюдений. В за информации.

связи с этим, в результате обработки годо-

Таблица 1. Данные для проведения регрессионно-корреляционного анализа, тыс. руб.

Показатели	31.12.2015 г.	31.12.2016 г.	31.12.2017 г.	31.12.2018 г.	31.12.2019 г.
У	3077	1554	13637	2956	14119
Х1	159584	312715	148670	121201	214227
Х2	153641	303554	119753	109719	187847
Х3	769	393	3411	745	3530
Х4	4115	2549	18683	4592	18194
Х5	10249	11013	8160	13485	13151
Х6	90226	101633	83661	75064	96001
Х7	16379	38206	12547	8321	5429
Х8	803	1394	1762	2989	438
Х9	1828	6612	10234	6875	8186
Х10	114493	174460	89169	81764	97100
Х11	1457	28922	3774	6709	18469
Х12	3819	5373	19011	21886	36006

Следует определить, все ли переменные ная из коэффициентов парной корреляции нужно включать в уравнение, для решения для всех 12 факторов.

этого была рассчитана таблица, составлен-

Таблица 2. Теснота связи, коэффициент ко		рреляции
Показатели	Условное обозначение	Коэффициент многофакторной корреляции, R	Процент вариации, фактора включенного в уравнение %
Выручка	Х1	-0,196848	3,87
Себестоимость	Х2	-0,321115	10,31
Текущий налог на прибыль	Х3	0,999999	99,99
Прибыль от продаж	Х4	0,998422	99,68
Основные средства	Х5	-0,196912	3,87
Дебиторская задол женность	Х6	-0,011376	0,01
Денежные средства	Х7	-0,583763	34,07
Прочие расходы	Х8	-0,345086	11,90
Управленческие рас ходы	Х9	0,682731	46,61
Кредиторская задол женность	Х10	-0,520499	27,09
Запасы	Х11	-0,131144	1,72
Собственный капитал	Х12	0,738800	54,58

Для дальнейшего построения модели необходимо исключить показатели со слабой факторной связью. Что свидетельствует об отсутствии мультиколлинеарности.

В связи с этим исключаются факторы X1, X2, Х5, Х6, Х7, Х8, Х9, Х10, Х11, а также Х3, так как он не актуален в исследовании [2].

Таким образом, уравнение регрессии приобрело вид:

У = b 0 b 1 x 4 – b 2 x 12

После предварительного отбора факторов на основе парных и частных коэффициентов корреляции была произведена оценка параметров и построено выборочное уравнение регрессии.

После многочисленных расчетов уравнение регрессии приобрело следующий вид:

У = 0,349x 12 + 0,772x 4 – 6378,24

Для определения тесноты связи между фактором Y и совокупностью факторов X4, X12 был применён коэффициент множественной корреляции R. Коэффициент изменяется в интервале от 0 до 1. Чем больше абсолютное значение парного коэффициента корреляции, тем более тесная взаимосвязь между данными двумя признаками.

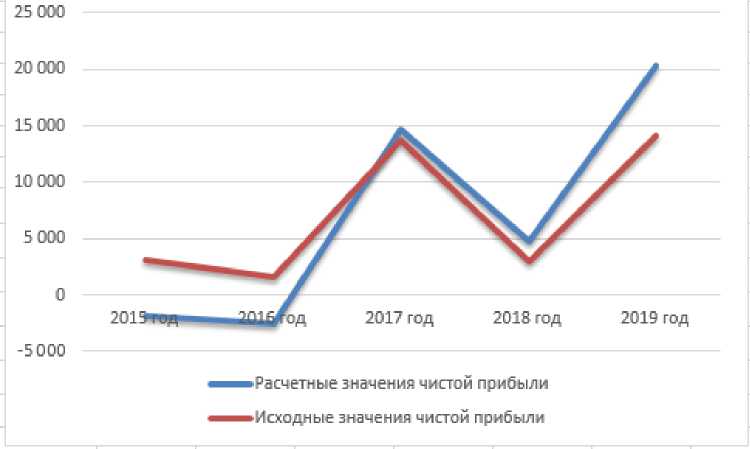
Рис. 1. Изменение чистой прибыли по уравнению регрессии

В нашем случае R = 0,73, что говорит о наличии функциональной связи.

Обычно интерпретируется не сам коэффициент корреляции R, а его квадрат R2, который называется коэффициентом множественной (общей) Он показывает, какая часть общей дисперсии объясняется за счёт вариации линейной комбинации аргументов Х4, Х12 при данных значениях коэффициентов регрессии. В нашем случае R2 = 0,5448, то есть 54,5 % вариации результативного признака объясняется фак- торами, включёнными в уравнение регрессии, а 45,5% – прочими факторами, которые мы не включили в модель.

Можно сделать вывод, что при увеличении прибыли от продаж на 1%, с вероятностью 99,9% чистая прибыль увеличится на 0,77 %. И аналогично увеличивая собственный капитал на 1% есть шанс в 54% увеличения чистой прибыли на 0,34%.

Из этого следует, что руководству следует обратить внимание на объем собст- венного капитала. Так как мы выяснили, что он тесно связан с изменением чистой прибыли. Поскольку постольку управление им способно оказать значительное влияние не только на финансовую устой чивость, но и как мы выяснили и на пла тежеспособность.

Список литературы Разработка модели финансового состояния, прогнозирование на основе множественной регрессии

Максимова Т.Г. Эконометрика: учебно-методическое пособие / Т.Г. Максимова, И.Н. Попова. - СПб.: Университет ИТМО, 2018. - 70 с.
Филобокова Л.Ю. Неформальные методы прогнозирования финансовой устойчивости малых предприятий // Экономический анализ: теория и практика. - 2018.-№9 (114). - С. 18-21.
Кован С.Е. Финансовая устойчивость предприятия и ее оценка для предупреждения банкротства // Экономический анализ: теория и практика.- 2018. - №15 (144). - С. 52-59.

Статья научная